|
Arc Length
Arc length is the distance between two points along a section of a curve. Development of a formulation of arc length suitable for applications to mathematics and the sciences is a problem in vector calculus and in differential geometry. In the most basic formulation of arc length for a vector valued curve (thought of as the trajectory of a particle), the arc length is obtained by integrating speed, the magnitude of the velocity vector over the curve with respect to time. Thus the length of a continuously differentiable curve (x(t),y(t)), for a\le t\le b, in the Euclidean plane is given as the integral L = \int_a^b \sqrt\,dt, (because \sqrt is the magnitude of the velocity vector (x'(t),y'(t)), i.e., the particle's speed). The defining integral of arc length does not always have a closed-form expression, and numerical integration may be used instead to obtain numerical values of arc length. Determining the length of an irregular arc segment by approximating the arc segment as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polygonal Chain
In geometry, a polygonal chain is a connected series of line segments. More formally, a polygonal chain is a curve specified by a sequence of points (A_1, A_2, \dots, A_n) called its vertices. The curve itself consists of the line segments connecting the consecutive vertices. Variations Simple A simple polygonal chain is one in which only consecutive segments intersect and only at their endpoints. Closed A closed polygonal chain is one in which the first vertex coincides with the last one, or, alternatively, the first and the last vertices are also connected by a line segment. A simple closed polygonal chain in the plane is the boundary of a simple polygon. Often the term "polygon" is used in the meaning of "closed polygonal chain", but in some cases it is important to draw a distinction between a polygonal area and a polygonal chain. A space closed polygonal chain is also known as a skew "polygon". Monotone A polygonal chain is called ''monotone'' if there is a strai ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
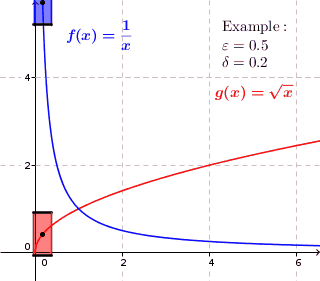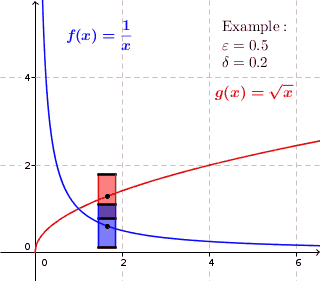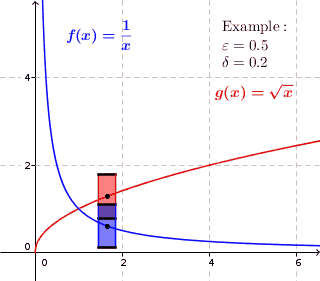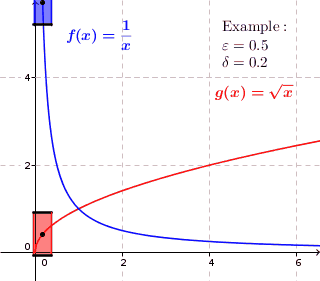
Uniform Continuity
In mathematics, a real function f of real numbers is said to be uniformly continuous if there is a positive real number \delta such that function values over any function domain interval of the size \delta are as close to each other as we want. In other words, for a uniformly continuous real function of real numbers, if we want function value differences to be less than any positive real number \varepsilon, then there is a positive real number \delta such that , f(x) - f(y), 0 there exists a real number \delta > 0 such that for every x,y \in X with d_1(x,y) 0 such that for every x,y \in X , , x - y, 0 \; \forall x \in X \; \forall y \in X : \, d_1(x,y) 0 , \forall x \in X , and \forall y \in X ) are used. * Equivalently, f is uniformly continuous if it admits a modulus of continuity. Definition of (ordinary) continuity * f is called continuous \underline if for every real number \varepsilon > 0 there exists a real number \delta > 0 such that for every y ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fundamental Theorem Of Calculus
The fundamental theorem of calculus is a theorem that links the concept of derivative, differentiating a function (mathematics), function (calculating its slopes, or rate of change at every point on its domain) with the concept of integral, integrating a function (calculating the area under its graph, or the cumulative effect of small contributions). Roughly speaking, the two operations can be thought of as inverses of each other. The first part of the theorem, the first fundamental theorem of calculus, states that for a continuous function , an antiderivative or indefinite integral can be obtained as the integral of over an interval with a variable upper bound. Conversely, the second part of the theorem, the second fundamental theorem of calculus, states that the integral of a function over a fixed Interval (mathematics), interval is equal to the change of any antiderivative between the ends of the interval. This greatly simplifies the calculation of a definite integral pr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Limit (mathematics)
In mathematics, a limit is the value that a function (or sequence) approaches as the argument (or index) approaches some value. Limits of functions are essential to calculus and mathematical analysis, and are used to define continuity, derivatives, and integrals. The concept of a limit of a sequence is further generalized to the concept of a limit of a topological net, and is closely related to limit and direct limit in category theory. The limit inferior and limit superior provide generalizations of the concept of a limit which are particularly relevant when the limit at a point may not exist. Notation In formulas, a limit of a function is usually written as : \lim_ f(x) = L, and is read as "the limit of of as approaches equals ". This means that the value of the function can be made arbitrarily close to , by choosing sufficiently close to . Alternatively, the fact that a function approaches the limit as approaches is sometimes denoted by a right arrow (→ or ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Continuously Differentiable
In mathematics, a differentiable function of one Real number, real variable is a Function (mathematics), function whose derivative exists at each point in its Domain of a function, domain. In other words, the Graph of a function, graph of a differentiable function has a non-Vertical tangent, vertical tangent line at each interior point in its domain. A differentiable function is Smoothness, smooth (the function is locally well approximated as a linear function at each interior point) and does not contain any break, angle, or Cusp (singularity), cusp. If is an interior point in the domain of a function , then is said to be ''differentiable at'' if the derivative f'(x_0) exists. In other words, the graph of has a non-vertical tangent line at the point . is said to be differentiable on if it is differentiable at every point of . is said to be ''continuously differentiable'' if its derivative is also a continuous function over the domain of the function f. Generally speaking, i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Signed Distance
In mathematics and its applications, the signed distance function or signed distance field (SDF) is the orthogonal distance of a given point ''x'' to the boundary of a set Ω in a metric space (such as the surface of a geometric shape), with the sign determined by whether or not ''x'' is in the interior of Ω. The function has positive values at points ''x'' inside Ω, it decreases in value as ''x'' approaches the boundary of Ω where the signed distance function is zero, and it takes negative values outside of Ω. However, the alternative convention is also sometimes taken instead (i.e., negative inside Ω and positive outside). The concept also sometimes goes by the name oriented distance function/field. Definition Let be a subset of a metric space with metric , and \partial\Omega be its boundary. The distance between a point of and the subset \partial\Omega of is defined as usual as : d(x, \partial \Omega) = \inf_d(x, y), where \inf denotes the infimum. The ''sig ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Curve Orientation
In mathematics, an orientation of a curve is the choice of one of the two possible directions for travelling on the curve. For example, for Cartesian coordinates, the -axis is traditionally oriented toward the right, and the -axis is upward oriented. In the case of a plane simple closed curve (that is, a curve in the plane whose starting point is also the end point and which has no other self-intersections), the curve is said to be positively oriented or counterclockwise oriented, if one always has the curve interior to the left (and consequently, the curve exterior to the right), when traveling on it. Otherwise, that is if left and right are exchanged, the curve is negatively oriented or clockwise oriented. This definition relies on the fact that every simple closed curve admits a well-defined interior, which follows from the Jordan curve theorem. The inner loop of a beltway road in a country where people drive on the right side of the road is an example of a negatively orie ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Origin (mathematics)
In mathematics, the origin of a Euclidean space is a special point, usually denoted by the letter ''O'', used as a fixed point of reference for the geometry of the surrounding space. In physical problems, the choice of origin is often arbitrary, meaning any choice of origin will ultimately give the same answer. This allows one to pick an origin point that makes the mathematics as simple as possible, often by taking advantage of some kind of geometric symmetry. Cartesian coordinates In a Cartesian coordinate system, the origin is the point where the axes of the system intersect.. The origin divides each of these axes into two halves, a positive and a negative semiaxis. Points can then be located with reference to the origin by giving their numerical coordinates—that is, the positions of their projections along each axis, either in the positive or negative direction. The coordinates of the origin are always all zero, for example (0,0) in two dimensions and (0,0,0) in three. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orientation (mathematics)
In mathematics, orientability is a property of some topological spaces such as real vector spaces, Euclidean spaces, surfaces, and more generally manifolds that allows a consistent definition of "clockwise" and "anticlockwise". A space is orientable if such a consistent definition exists. In this case, there are two possible definitions, and a choice between them is an orientation of the space. Real vector spaces, Euclidean spaces, and spheres are orientable. A space is non-orientable if "clockwise" is changed into "counterclockwise" after running through some loops in it, and coming back to the starting point. This means that a geometric shape, such as , that moves continuously along such a loop is changed into its own mirror image . A Möbius strip is an example of a non-orientable space. Various equivalent formulations of orientability can be given, depending on the desired application and level of generality. Formulations applicable to general topological manifolds oft ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Arbitrarily Large
In mathematics, the phrases arbitrarily large, arbitrarily small and arbitrarily long are used in statements to make clear the fact that an object is large, small, or long with little limitation or restraint, respectively. The use of "arbitrarily" often occurs in the context of real numbers (and its subsets thereof), though its meaning can differ from that of "sufficiently" and "infinitely". Examples The statement : "f(x) is non-negative for arbitrarily large ''x''." is a shorthand for: : "For every real number ''n'', f(x) is non-negative for some value of ''x'' greater than ''n''." In the common parlance, the term "arbitrarily long" is often used in the context of sequence of numbers. For example, to say that there are "arbitrarily long arithmetic progressions of prime numbers" does not mean that there exists any infinitely long arithmetic progression of prime numbers (there is not), nor that there exists any particular arithmetic progression of prime numbers that is in some ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chord (geometry)
A chord (from the Latin ''chorda'', meaning " bowstring") of a circle is a straight line segment whose endpoints both lie on a circular arc. If a chord were to be extended infinitely on both directions into a line, the object is a ''secant line''. The perpendicular line passing through the chord's midpoint is called '' sagitta'' (Latin for "arrow"). More generally, a chord is a line segment joining two points on any curve, for instance, on an ellipse. A chord that passes through a circle's center point is the circle's ''diameter''. In circles Among properties of chords of a circle are the following: # Chords are equidistant from the center if and only if their lengths are equal. # Equal chords are subtended by equal angles from the center of the circle. # A chord that passes through the center of a circle is called a diameter and is the longest chord of that specific circle. # If the line extensions (secant lines) of chords AB and CD intersect at a point P, then their ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |