|
3D Shape
Solid geometry or stereometry is the geometry of Three-dimensional space, three-dimensional Euclidean space (3D space). A solid figure is the region (mathematics), region of 3D space bounded by a two-dimensional closed surface; for example, a solid ball (mathematics), ball consists of a sphere and its Interior (topology), interior. Solid geometry deals with the measurements of volumes of various solids, including Pyramid (geometry), pyramids, Prism (geometry), prisms (and other polyhedrons), cubes, Cylinder (geometry), cylinders, cone (geometry), cones (and Frustum, truncated cones). History The Pythagoreanism, Pythagoreans dealt with the regular solids, but the pyramid, prism, cone and cylinder were not studied until the Platonism, Platonists. Eudoxus of Cnidus, Eudoxus established their measurement, proving the pyramid and cone to have one-third the volume of a prism and cylinder on the same base and of the same height. He was probably also the discoverer of a proof that t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
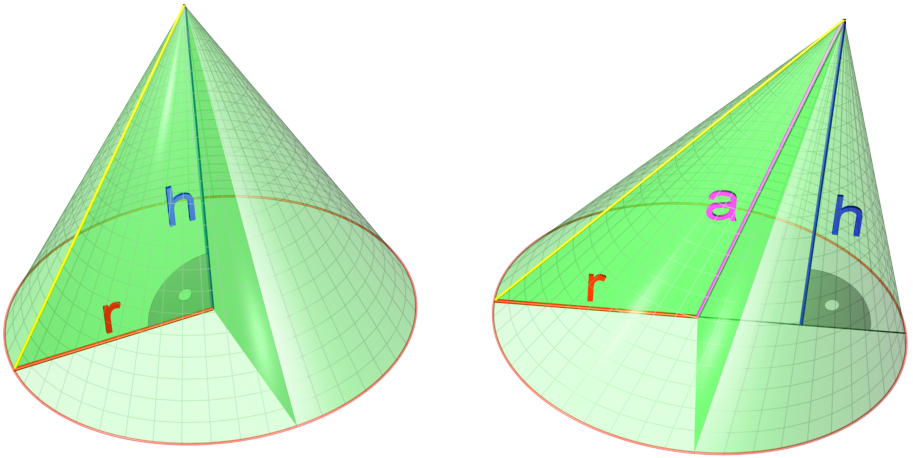
Cone (geometry)
In geometry, a cone is a three-dimensional figure that tapers smoothly from a flat base (typically a circle) to a point not contained in the base, called the '' apex'' or '' vertex''. A cone is formed by a set of line segments, half-lines, or lines connecting a common point, the apex, to all of the points on a base. In the case of line segments, the cone does not extend beyond the base, while in the case of half-lines, it extends infinitely far. In the case of lines, the cone extends infinitely far in both directions from the apex, in which case it is sometimes called a ''double cone''. Each of the two halves of a double cone split at the apex is called a ''nappe''. Depending on the author, the base may be restricted to a circle, any one-dimensional quadratic form in the plane, any closed one-dimensional figure, or any of the above plus all the enclosed points. If the enclosed points are included in the base, the cone is a solid object; otherwise it is an open surface ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cube (geometry)
A cube or regular hexahedron is a three-dimensional space, three-dimensional solid object in geometry, which is bounded by six congruent square (geometry), square faces, a type of polyhedron. It has twelve congruent edges and eight vertices. It is a type of parallelepiped, with pairs of parallel opposite faces, and more specifically a rhombohedron, with congruent edges, and a rectangular cuboid, with right angles between pairs of intersecting faces and pairs of intersecting edges. It is an example of many classes of polyhedra: Platonic solid, regular polyhedron, parallelohedron, zonohedron, and plesiohedron. The dual polyhedron of a cube is the regular octahedron. The cube can be represented in many ways, one of which is the graph known as the cubical graph. It can be constructed by using the Cartesian product of graphs. The cube is the three-dimensional hypercube, a family of polytopes also including the two-dimensional square and four-dimensional tesseract. A cube with 1, unit s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Solid Angle
In geometry, a solid angle (symbol: ) is a measure of the amount of the field of view from some particular point that a given object covers. That is, it is a measure of how large the object appears to an observer looking from that point. The point from which the object is viewed is called the ''apex'' of the solid angle, and the object is said to '' subtend'' its solid angle at that point. In the International System of Units (SI), a solid angle is expressed in a dimensionless unit called a ''steradian'' (symbol: sr), which is equal to one square radian, sr = rad2. One steradian corresponds to one unit of area (of any shape) on the unit sphere surrounding the apex, so an object that blocks all rays from the apex would cover a number of steradians equal to the total surface area of the unit sphere, 4\pi. Solid angles can also be measured in squares of angular measures such as degrees, minutes, and seconds. A small object nearby may subtend the same solid angle as a larger object ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Line (mathematics)
In geometry, a straight line, usually abbreviated line, is an infinitely long object with no width, depth, or curvature, an idealization of such physical objects as a straightedge, a taut string, or a ray of light. Lines are spaces of dimension one, which may be embedded in spaces of dimension two, three, or higher. The word ''line'' may also refer, in everyday life, to a line segment, which is a part of a line delimited by two points (its ''endpoints''). Euclid's ''Elements'' defines a straight line as a "breadthless length" that "lies evenly with respect to the points on itself", and introduced several postulates as basic unprovable properties on which the rest of geometry was established. ''Euclidean line'' and ''Euclidean geometry'' are terms introduced to avoid confusion with generalizations introduced since the end of the 19th century, such as non-Euclidean, projective, and affine geometry. Properties In the Greek deductive geometry of Euclid's ''Elements'', ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Plane (geometry)
In mathematics, a Euclidean plane is a Euclidean space of dimension two, denoted \textbf^2 or \mathbb^2. It is a geometric space in which two real numbers are required to determine the position of each point. It is an affine space, which includes in particular the concept of parallel lines. It has also metrical properties induced by a distance, which allows to define circles, and angle measurement. A Euclidean plane with a chosen Cartesian coordinate system is called a '' Cartesian plane''. The set \mathbb^2 of the ordered pairs of real numbers (the real coordinate plane), equipped with the dot product, is often called ''the'' Euclidean plane or ''standard Euclidean plane'', since every Euclidean plane is isomorphic to it. History Books I through IV and VI of Euclid's Elements dealt with two-dimensional geometry, developing such notions as similarity of shapes, the Pythagorean theorem (Proposition 47), equality of angles and areas, parallelism, the sum of the angles ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Incidence (geometry)
In geometry, an incidence relation is a heterogeneous relation that captures the idea being expressed when phrases such as "a point ''lies on'' a line" or "a line is ''contained in'' a plane" are used. The most basic incidence relation is that between a point, , and a line, , sometimes denoted . If ''P'' and ''l'' are incident, , the pair is called a ''flag''. There are many expressions used in common language to describe incidence (for example, a line ''passes through'' a point, a point ''lies in'' a plane, etc.) but the term "incidence" is preferred because it does not have the additional connotations that these other terms have, and it can be used in a symmetric manner. Statements such as "line intersects line " are also statements about incidence relations, but in this case, it is because this is a shorthand way of saying that "there exists a point that is incident with both line and line ". When one type of object can be thought of as a set of the other type of object (''vi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
1911 Encyclopædia Britannica
Events January * January 1 – A decade after federation, the Northern Territory and the Australian Capital Territory are added to the Commonwealth of Australia. * January 3 ** 1911 Kebin earthquake: An earthquake of 7.7 Moment magnitude scale, moment magnitude strikes near Almaty in Russian Turkestan, killing 450 or more people. ** Siege of Sidney Street in London: Two Latvian people, Latvian anarchists die, after a seven-hour siege against a combined police and military force. Home Secretary Winston Churchill arrives to oversee events. * January 4 – Comparison of the Amundsen and Scott expeditions, Amundsen and Scott expeditions: Robert Falcon Scott's British Terra Nova Expedition, ''Terra Nova'' Expedition to the South Pole arrives in the Antarctic and establishes a base camp at Cape Evans on Ross Island. * January 5 – Egypt's Zamalek SC is founded as a general sports and Association football club by Belgian lawyer George Merzbach as Q ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Radius
In classical geometry, a radius (: radii or radiuses) of a circle or sphere is any of the line segments from its Centre (geometry), center to its perimeter, and in more modern usage, it is also their length. The radius of a regular polygon is the line segment or distance from its center to any of its Vertex (geometry), vertices. The name comes from the Latin ''radius'', meaning ray but also the spoke of a chariot wheel.Definition of Radius at dictionary.reference.com. Accessed on 2009-08-08. The typical abbreviation and mathematical symbol for radius is ''R'' or ''r''. By extension, the diameter ''D'' is defined as twice the radius:Definition of radius at mathwords.com. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Eudoxus Of Cnidus
Eudoxus of Cnidus (; , ''Eúdoxos ho Knídios''; ) was an Ancient Greece, ancient Greek Ancient Greek astronomy, astronomer, Greek mathematics, mathematician, doctor, and lawmaker. He was a student of Archytas and Plato. All of his original works are lost, though some fragments are preserved in Hipparchus' ''Commentaries on the Phenomena of Aratus and Eudoxus''. ''Theodosius' Spherics, Spherics'' by Theodosius of Bithynia may be based on a work by Eudoxus. Life Eudoxus, son of Aeschines, was born and died in Cnidus (also transliterated Knidos), a city on the southwest coast of Anatolia. The years of Eudoxus' birth and death are not fully known but Diogenes Laertius, Diogenes Laërtius gave several biographical details, mentioned that Apollodorus of Athens, Apollodorus said he reached his wikt:acme#English, acme in the 103rd Olympiad (368–), and claimed he died in his 53rd year. From this 19th century mathematical historians reconstructed dates of 408–, but 20th century schola ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Platonism
Platonism is the philosophy of Plato and philosophical systems closely derived from it, though contemporary Platonists do not necessarily accept all doctrines of Plato. Platonism has had a profound effect on Western thought. At the most fundamental level, Platonism affirms the existence of abstract objects, which are asserted to exist in a third realm distinct from both the sensible external world and from the internal world of consciousness, and is the opposite of nominalism." Philosophers who affirm the existence of abstract objects are sometimes called platonists; those who deny their existence are sometimes called nominalists. The terms "platonism" and "nominalism" have established senses in the history of philosophy, where they denote positions that have little to do with the modern notion of an abstract object. In this connection, it is essential to bear in mind that modern platonists (with a small 'p') need not accept any of the doctrines of Plato, just as modern nomina ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |