Young–Laplace equation on:
[Wikipedia]
[Google]
[Amazon]
In
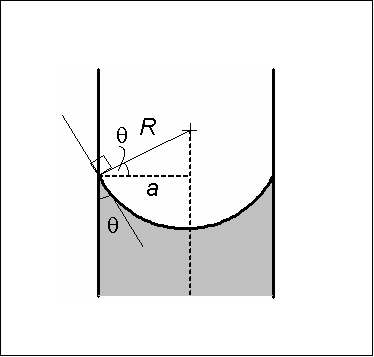 In a sufficiently narrow (i.e., low Bond number) tube of circular cross-section (radius ''a''), the interface between two fluids forms a meniscus that is a portion of the surface of a sphere with radius ''R''. The pressure jump across this surface is related to the radius and the surface tension γ by
This may be shown by writing the Young–Laplace equation in spherical form with a contact angle boundary condition and also a prescribed height boundary condition at, say, the bottom of the meniscus. The solution is a portion of a sphere, and the solution will exist ''only'' for the pressure difference shown above. This is significant because there isn't another equation or law to specify the pressure difference; existence of solution for one specific value of the pressure difference prescribes it.
The radius of the sphere will be a function only of the contact angle, θ, which in turn depends on the exact properties of the fluids and the container material with which the fluids in question are contacting/interfacing:
so that the pressure difference may be written as:
In a sufficiently narrow (i.e., low Bond number) tube of circular cross-section (radius ''a''), the interface between two fluids forms a meniscus that is a portion of the surface of a sphere with radius ''R''. The pressure jump across this surface is related to the radius and the surface tension γ by
This may be shown by writing the Young–Laplace equation in spherical form with a contact angle boundary condition and also a prescribed height boundary condition at, say, the bottom of the meniscus. The solution is a portion of a sphere, and the solution will exist ''only'' for the pressure difference shown above. This is significant because there isn't another equation or law to specify the pressure difference; existence of solution for one specific value of the pressure difference prescribes it.
The radius of the sphere will be a function only of the contact angle, θ, which in turn depends on the exact properties of the fluids and the container material with which the fluids in question are contacting/interfacing:
so that the pressure difference may be written as:
 In order to maintain
In order to maintain
"An account of some experiments shown before the Royal Society; with an enquiry into the cause of some of the ascent and suspension of water in capillary tubes,"
''Philosophical Transactions of the Royal Society of London'', 30 : 739–747. * James Jurin (1719
"An account of some new experiments, relating to the action of glass tubes upon water and quicksilver,"
''Philosophical Transactions of the Royal Society of London'', 30 : 1083–1096. For a water-filled glass tube in air at
Pierre Simon Laplace (1749–1827)
, in ''A Short Account of the History of Mathematics'', 4th ed., Dover,
physics
Physics is the natural science that studies matter, its fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge which ...
, the Young–Laplace equation () is an algebraic equation that describes the capillary pressure In fluid statics, capillary pressure () is the pressure between two immiscible fluids in a thin tube (see capillary action), resulting from the interactions of forces between the fluids and solid walls of the tube. Capillary pressure can serve as bo ...
difference sustained across the interface between two static fluids, such as water
Water (chemical formula ) is an inorganic, transparent, tasteless, odorless, and nearly colorless chemical substance, which is the main constituent of Earth's hydrosphere and the fluids of all known living organisms (in which it acts as ...
and air, due to the phenomenon of surface tension
Surface tension is the tendency of liquid surfaces at rest to shrink into the minimum surface area possible. Surface tension is what allows objects with a higher density than water such as razor blades and insects (e.g. water striders) t ...
or wall tension
In mechanics, a cylinder stress is a stress distribution with rotational symmetry; that is, which remains unchanged if the stressed object is rotated about some fixed axis.
Cylinder stress patterns include:
* circumferential stress, or hoop stre ...
, although use of the latter is only applicable if assuming that the wall is very thin. The Young–Laplace equation relates the pressure difference to the shape of the surface or wall and it is fundamentally important in the study of static capillary surfaces. It's a statement of normal stress balance for static fluids meeting at an interface, where the interface is treated as a surface (zero thickness):
where is the Laplace pressure, the pressure difference across the fluid interface (the exterior pressure minus the interior pressure), is the surface tension
Surface tension is the tendency of liquid surfaces at rest to shrink into the minimum surface area possible. Surface tension is what allows objects with a higher density than water such as razor blades and insects (e.g. water striders) t ...
(or wall tension
In mechanics, a cylinder stress is a stress distribution with rotational symmetry; that is, which remains unchanged if the stressed object is rotated about some fixed axis.
Cylinder stress patterns include:
* circumferential stress, or hoop stre ...
), is the unit normal pointing out of the surface, is the mean curvature, and and are the principal radii of curvature. Note that only normal stress is considered, this is because it has been shown that a static interface is possible only in the absence of tangential stress.
The equation is named after Thomas Young, who developed the qualitative theory of surface tension in 1805, and Pierre-Simon Laplace
Pierre-Simon, marquis de Laplace (; ; 23 March 1749 – 5 March 1827) was a French scholar and polymath whose work was important to the development of engineering, mathematics, statistics, physics, astronomy, and philosophy. He summarize ...
who completed the mathematical description in the following year. It is sometimes also called the Young–Laplace–Gauss equation, as Carl Friedrich Gauss unified the work of Young and Laplace in 1830, deriving both the differential equation and boundary conditions using Johann Bernoulli's virtual work principles.
Soap films
If the pressure difference is zero, as in a soap film without gravity, the interface will assume the shape of a minimal surface.Emulsions
The equation also explains the energy required to create anemulsion
An emulsion is a mixture of two or more liquids that are normally immiscible (unmixable or unblendable) owing to liquid-liquid phase separation. Emulsions are part of a more general class of two-phase systems of matter called colloids. Alth ...
. To form the small, highly curved droplets of an emulsion, extra energy is required to overcome the large pressure that results from their small radius.
The Laplace pressure, which is greater for smaller droplets, causes the diffusion of molecules out of the smallest droplets in an emulsion and drives emulsion coarsening via Ostwald ripening.
Capillary pressure in a tube
hydrostatic equilibrium
In fluid mechanics, hydrostatic equilibrium (hydrostatic balance, hydrostasy) is the condition of a fluid or plastic solid at rest, which occurs when external forces, such as gravity, are balanced by a pressure-gradient force. In the planeta ...
, the induced capillary pressure is balanced by a change in height, ''h'', which can be positive or negative, depending on whether the wetting angle is less than or greater than 90°. For a fluid of density
Density (volumetric mass density or specific mass) is the substance's mass per unit of volume. The symbol most often used for density is ''ρ'' (the lower case Greek letter rho), although the Latin letter ''D'' can also be used. Mathematicall ...
ρ:
where ''g'' is the gravitational acceleration
In physics, gravitational acceleration is the acceleration of an object in free fall within a vacuum (and thus without experiencing drag). This is the steady gain in speed caused exclusively by the force of gravitational attraction. All bodie ...
. This is sometimes known as the Jurin's law or Jurin height after James Jurin
James Jurin FRS FRCP (baptised 15 December 168429 March 1750) was an English scientist and physician, particularly remembered for his early work in capillary action and in the epidemiology of smallpox vaccination. He was a staunch proponent o ...
who studied the effect in 1718.See:
* James Jurin (1718"An account of some experiments shown before the Royal Society; with an enquiry into the cause of some of the ascent and suspension of water in capillary tubes,"
''Philosophical Transactions of the Royal Society of London'', 30 : 739–747. * James Jurin (1719
"An account of some new experiments, relating to the action of glass tubes upon water and quicksilver,"
''Philosophical Transactions of the Royal Society of London'', 30 : 1083–1096. For a water-filled glass tube in air at
sea level
Mean sea level (MSL, often shortened to sea level) is an average surface level of one or more among Earth's coastal bodies of water from which heights such as elevation may be measured. The global MSL is a type of vertical datuma standardis ...
:
*γ = 0.0728 J/m2 at 20 ° C
*''θ'' = 20° (0.35 rad)
*''ρ'' = 1000 kg/m3
*''g'' = 9.8 m/s2
and so the height of the water column is given by:
Thus for a 2 mm wide (1 mm radius) tube, the water would rise 14 mm. However, for a capillary tube with radius 0.1 mm, the water would rise 14 cm (about 6 inch
Measuring tape with inches
The inch (symbol: in or ″) is a unit of length in the British imperial and the United States customary systems of measurement. It is equal to yard or of a foot. Derived from the Roman uncia ("twelfth ...
es).
Capillary action in general
In the general case, for a free surface and where there is an applied "over-pressure", Δ''p'', at the interface in equilibrium, there is a balance between the applied pressure, thehydrostatic pressure
Fluid statics or hydrostatics is the branch of fluid mechanics that studies the condition of the equilibrium of a floating body and submerged body " fluids at hydrostatic equilibrium and the pressure in a fluid, or exerted by a fluid, on an i ...
and the effects of surface tension. The Young–Laplace equation becomes:
The equation can be non-dimensionalised in terms of its characteristic length-scale, the capillary length:
and characteristic pressure
For clean water at standard temperature and pressure
Standard temperature and pressure (STP) are standard sets of conditions for experimental measurements to be established to allow comparisons to be made between different sets of data. The most used standards are those of the International Union ...
, the capillary length is ~2 mm.
The non-dimensional equation then becomes:
Thus, the surface shape is determined by only one parameter, the over pressure of the fluid, Δ''p''* and the scale of the surface is given by the capillary length. The solution of the equation requires an initial condition for position, and the gradient of the surface at the start point.
Axisymmetric equations
The (nondimensional) shape, ''r''(''z'') of anaxisymmetric
Rotational symmetry, also known as radial symmetry in geometry, is the property a shape has when it looks the same after some rotation by a partial turn. An object's degree of rotational symmetry is the number of distinct orientations in which i ...
surface can be found by substituting general expressions for principal curvature
In differential geometry, the two principal curvatures at a given point of a surface are the maximum and minimum values of the curvature as expressed by the eigenvalues of the shape operator at that point. They measure how the surface bends b ...
s to give the hydrostatic Young–Laplace equations:
Application in medicine
Inmedicine
Medicine is the science and practice of caring for a patient, managing the diagnosis, prognosis, prevention, treatment, palliation of their injury or disease, and promoting their health. Medicine encompasses a variety of health care pr ...
it is often referred to as the Law of Laplace, used in the context of cardiovascular physiology, and also respiratory physiology, though the latter use is often erroneous.
History
Francis Hauksbee performed some of the earliest observations and experiments in 1709 and these were repeated in 1718 byJames Jurin
James Jurin FRS FRCP (baptised 15 December 168429 March 1750) was an English scientist and physician, particularly remembered for his early work in capillary action and in the epidemiology of smallpox vaccination. He was a staunch proponent o ...
who observed that the height of fluid in a capillary column was a function only of the cross-sectional area at the surface, not of any other dimensions of the column.
Thomas Young laid the foundations of the equation in his 1804 paper ''An Essay on the Cohesion of Fluids'' where he set out in descriptive terms the principles governing contact between fluids (along with many other aspects of fluid behaviour). Pierre Simon Laplace followed this up in ''Mécanique Céleste'' with the formal mathematical description given above, which reproduced in symbolic terms the relationship described earlier by Young.
Laplace accepted the idea propounded by Hauksbee in his book ''Physico-mechanical Experiments'' (1709), that the phenomenon was due to a force of attraction that was insensible at sensible distances. The part which deals with the action of a solid
Solid is one of the four fundamental states of matter (the others being liquid, gas, and plasma). The molecules in a solid are closely packed together and contain the least amount of kinetic energy. A solid is characterized by structur ...
on a liquid
A liquid is a nearly incompressible fluid that conforms to the shape of its container but retains a (nearly) constant volume independent of pressure. As such, it is one of the four fundamental states of matter (the others being solid, gas, ...
and the mutual action of two liquids was not worked out thoroughly, but ultimately was completed by Carl Friedrich Gauss. Franz Ernst Neumann
Franz Ernst Neumann (11 September 1798 – 23 May 1895) was a German mineralogist, physicist and mathematician.
Biography
Neumann was born in Joachimsthal, Margraviate of Brandenburg, near Berlin. In 1815 he interrupted his studies at Berlin ...
(1798-1895) later filled in a few details. Rouse Ball, W. W. 908
__NOTOC__
Year 908 ( CMVIII) was a leap year starting on Friday (link will display the full calendar) of the Julian calendar.
Events
By place
Byzantine Empire
* May 15 – The three-year-old Constantine VII, the son of Emperor Le ...
(2003)Pierre Simon Laplace (1749–1827)
, in ''A Short Account of the History of Mathematics'', 4th ed., Dover,
References
Further reading
* *Batchelor, G. K. (1967) ''An Introduction To Fluid Dynamics'', Cambridge University Press * *Tadros T. F. (1995) ''Surfactants in Agrochemicals'', Surfactant Science series, vol.54, DekkerExternal links
{{DEFAULTSORT:Young-Laplace equation Fluid dynamics Physiology Partial differential equations Mathematics in medicine Respiratory therapy Equations of fluid dynamics