YCbCr on:
[Wikipedia]
[Google]
[Amazon]

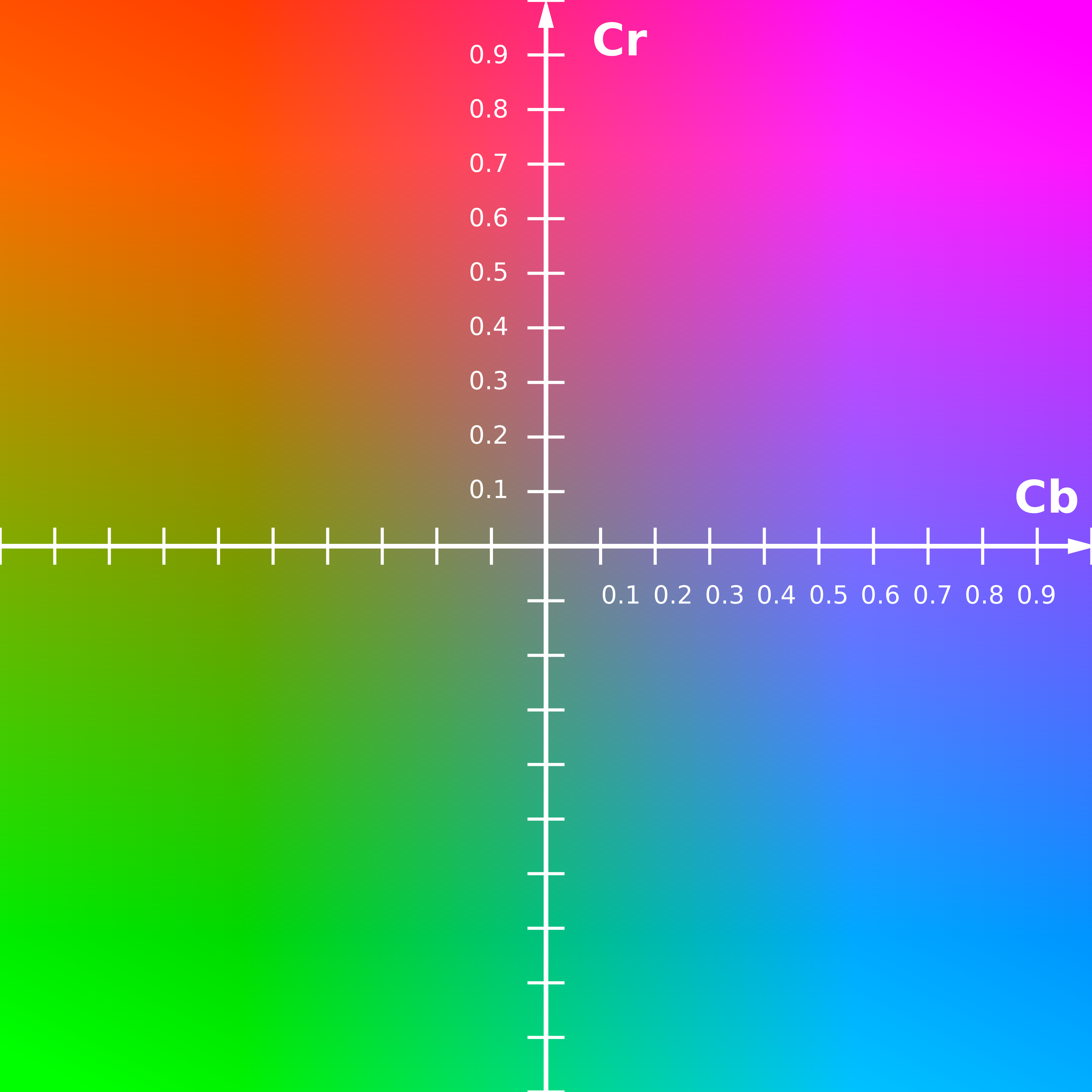 YCbCr, Y′CbCr, or Y Pb/Cb Pr/Cr, also written as YCBCR or Y′CBCR, is a family of
YCbCr, Y′CbCr, or Y Pb/Cb Pr/Cr, also written as YCBCR or Y′CBCR, is a family of
ITU-T H.273
Nevertheless that rule does not apply to P3-D65 primaries used by Netflix with BT.2020-NCL matrix, so that means matrix was not derived from primaries, but now Netflix allows BT.2020 primaries (since 2021). Same happens with JPEG: it has BT.601 matrix derived from System M primaries, yet the primaries of most images are BT.709.
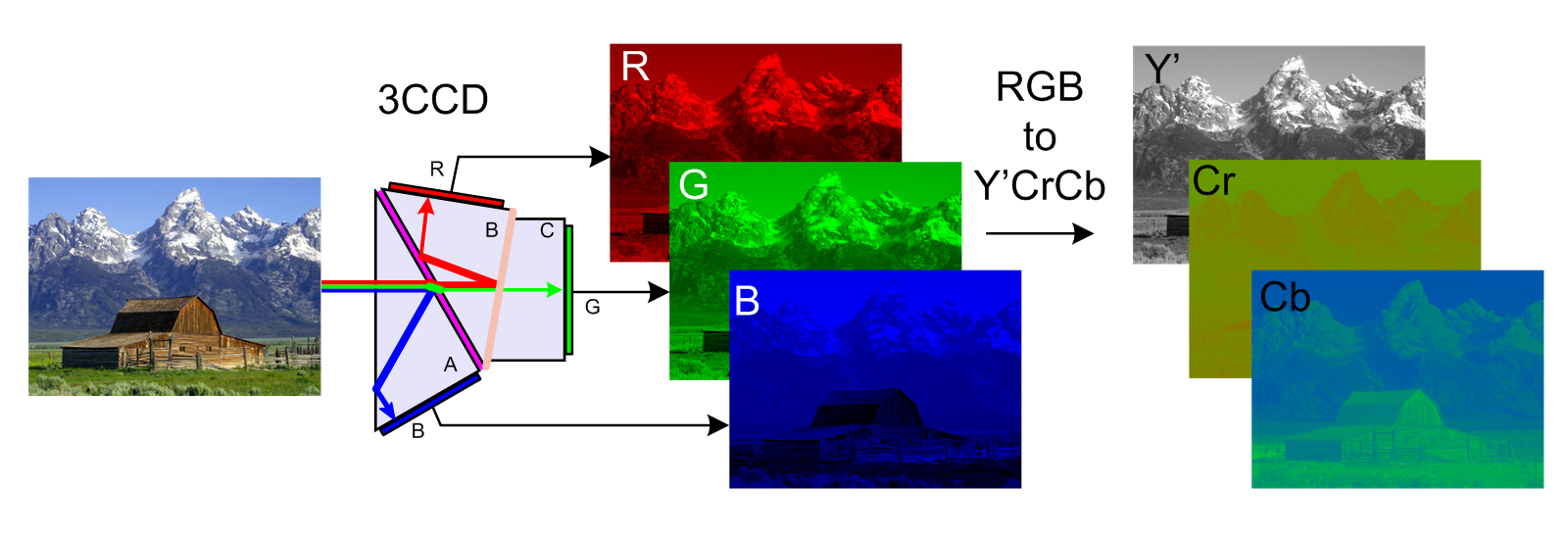 Y′CbCr signals (prior to scaling and offsets to place the signals into digital form) are called
Y′CbCr signals (prior to scaling and offsets to place the signals into digital form) are called
 A different form of Y′CbCr is specified in the ITU-R BT.709 standard, primarily for
A different form of Y′CbCr is specified in the ITU-R BT.709 standard, primarily for
Y'CbCr calculator
including BT.1886
Color Space Visualization
YCbCr Definition
{{Color space Color space
 YCbCr, Y′CbCr, or Y Pb/Cb Pr/Cr, also written as YCBCR or Y′CBCR, is a family of
YCbCr, Y′CbCr, or Y Pb/Cb Pr/Cr, also written as YCBCR or Y′CBCR, is a family of color space
A color space is a specific organization of colors. In combination with color profiling supported by various physical devices, it supports reproducible representations of colorwhether such representation entails an analog or a digital represent ...
s used as a part of the color image pipeline An image pipeline or video pipeline is the set of components commonly used between an image source (such as a camera, a scanner, or the rendering engine in a computer game), and an image renderer (such as a television set, a computer screen, a compu ...
in video
Video is an electronic medium for the recording, copying, playback, broadcasting, and display of moving visual media. Video was first developed for mechanical television systems, which were quickly replaced by cathode-ray tube (CRT) syste ...
and digital photography
Digital photography uses cameras containing arrays of electronic photodetectors interfaced to an analog-to-digital converter (ADC) to produce images focused by a lens, as opposed to an exposure on photographic film. The digitized image is sto ...
systems. Y′ is the luma
Luma or LUMA may refer to:
Arts
* La Trobe University Museum of Art, Melbourne, Australia
* LUMA Projection Arts Festival, an annual event featuring building-scale projection mapping and light installations in Binghamton, NY
* LUMA Foundation, ...
component and CB and CR are the blue-difference and red-difference chroma components. Y′ (with prime
A prime number (or a prime) is a natural number greater than 1 that is not a product of two smaller natural numbers. A natural number greater than 1 that is not prime is called a composite number. For example, 5 is prime because the only ways ...
) is distinguished from Y, which is luminance
Luminance is a photometric measure of the luminous intensity per unit area of light travelling in a given direction. It describes the amount of light that passes through, is emitted from, or is reflected from a particular area, and falls withi ...
, meaning that light intensity is nonlinearly encoded based on gamma corrected RGB
The RGB color model is an additive color model in which the red, green and blue primary colors of light are added together in various ways to reproduce a broad array of colors. The name of the model comes from the initials of the three addi ...
primaries.
Y′CbCr color spaces are defined by a mathematical coordinate transformation
In geometry, a coordinate system is a system that uses one or more numbers, or coordinates, to uniquely determine the position of the points or other geometric elements on a manifold such as Euclidean space. The order of the coordinates is sig ...
from an associated RGB
The RGB color model is an additive color model in which the red, green and blue primary colors of light are added together in various ways to reproduce a broad array of colors. The name of the model comes from the initials of the three addi ...
primaries and white point. If the underlying RGB color space is absolute, the Y′CbCr color space is an absolute color space
A color space is a specific organization of colors. In combination with color profiling supported by various physical devices, it supports reproducible representations of colorwhether such representation entails an analog or a digital represent ...
as well; conversely, if the RGB space is ill-defined, so is Y′CbCr. The transformation is defined iITU-T H.273
Nevertheless that rule does not apply to P3-D65 primaries used by Netflix with BT.2020-NCL matrix, so that means matrix was not derived from primaries, but now Netflix allows BT.2020 primaries (since 2021). Same happens with JPEG: it has BT.601 matrix derived from System M primaries, yet the primaries of most images are BT.709.
Rationale
Cathode ray tube
A cathode-ray tube (CRT) is a vacuum tube containing one or more electron guns, which emit electron beams that are manipulated to display images on a phosphorescent screen. The images may represent electrical waveforms ( oscilloscope), pictu ...
displays are driven by red, green, and blue voltage signals, but these RGB
The RGB color model is an additive color model in which the red, green and blue primary colors of light are added together in various ways to reproduce a broad array of colors. The name of the model comes from the initials of the three addi ...
signals are not efficient as a representation for storage and transmission, since they have a lot of redundancy.
YCbCr and Y′CbCr are a practical approximation to color processing and perceptual uniformity, where the primary color
A set (mathematics), set of primary colors or primary colours (see American and British English spelling differences#-our, -or, spelling differences) consists of colorants or colored lights that can be mixed in varying amounts to produce a gamu ...
s corresponding roughly to red, green and blue are processed into perceptually meaningful information. By doing this, subsequent image/video processing, transmission and storage can do operations and introduce errors in perceptually meaningful ways. Y′CbCr is used to separate out a luma signal (Y′) that can be stored with high resolution or transmitted at high bandwidth, and two chroma components (CB and CR) that can be bandwidth-reduced, subsampled, compressed, or otherwise treated separately for improved system efficiency.
One practical example would be decreasing the bandwidth or resolution allocated to "color" compared to "black and white", since humans are more sensitive to the black-and-white information (see image example to the right). This is called chroma subsampling
Chroma subsampling is the practice of encoding images by implementing less resolution for chroma information than for luma information, taking advantage of the human visual system's lower acuity for color differences than for luminance.
It is u ...
.
CbCr
YCbCr is sometimes abbreviated to YCC. Typically the terms Y′CbCr, YCbCr,YPbPr
YPbPr or Y'PbPr, also written as , is a color space used in video electronics, in particular in reference to component video cables. YPBPR is gamma corrected YCBCR color space (it is not analog YUV that was used for analog TV, though component ...
and YUV
YUV is a color model typically used as part of a color image pipeline. It encodes a color image or video taking human perception into account, allowing reduced bandwidth for chrominance components, compared to a "direct" RGB-representation. H ...
are used interchangeably, leading to some confusion. The main difference is that YPbPr is used with analog
Analog or analogue may refer to:
Computing and electronics
* Analog signal, in which information is encoded in a continuous variable
** Analog device, an apparatus that operates on analog signals
*** Analog electronics, circuits which use analog ...
images and YCbCr with digital images, leading to difference scaling values for Umax and Vmax (in YCbCr both are ) when converting to/from YUV. Y'CbCr and YCbCr differ due to the values being gamma corrected or not.
The equations below give a better picture of the common principles and general differences between these formats.
RGB conversion
R'G'B' to Y'PbPr
 Y′CbCr signals (prior to scaling and offsets to place the signals into digital form) are called
Y′CbCr signals (prior to scaling and offsets to place the signals into digital form) are called YPbPr
YPbPr or Y'PbPr, also written as , is a color space used in video electronics, in particular in reference to component video cables. YPBPR is gamma corrected YCBCR color space (it is not analog YUV that was used for analog TV, though component ...
, and are created from the corresponding gamma-adjusted RGB
The RGB color model is an additive color model in which the red, green and blue primary colors of light are added together in various ways to reproduce a broad array of colors. The name of the model comes from the initials of the three addi ...
(red, green and blue) source using three defined constants KR, KG, and KB as follows:
:
where KR, KG, and KB are ordinarily derived from the definition of the corresponding RGB space, and required to satisfy .
The equivalent matrix
Matrix most commonly refers to:
* ''The Matrix'' (franchise), an American media franchise
** ''The Matrix'', a 1999 science-fiction action film
** "The Matrix", a fictional setting, a virtual reality environment, within ''The Matrix'' (franchis ...
manipulation is often referred to as the "color matrix":
:
And its inverse:
:
Here, the prime (′) symbols mean gamma correction
Gamma correction or gamma is a nonlinear operation used to encode and decode luminance or tristimulus values in video or still image systems. Gamma correction is, in the simplest cases, defined by the following power-law expression:
: V_\tex ...
is being used; thus R′, G′ and B′ nominally range from 0 to 1, with 0 representing the minimum intensity (e.g., for display of the color black
Black is a color which results from the absence or complete absorption of visible light. It is an achromatic color, without hue, like white and grey. It is often used symbolically or figuratively to represent darkness. Black and white ...
) and 1 the maximum (e.g., for display of the color white
White is the lightest color and is achromatic (having no hue). It is the color of objects such as snow, chalk, and milk, and is the opposite of black. White objects fully reflect and scatter all the visible wavelengths of light. White on ...
). The resulting luma (Y) value will then have a nominal range from 0 to 1, and the chroma (PB and PR) values will have a nominal range from -0.5 to +0.5. The reverse conversion process can be readily derived by inverting the above equations.
Y'PbPr to Y'CbCr
When representing the signals in digital form, the results are scaled and rounded, and offsets are typically added. For example, the scaling and offset applied to the Y′ component per specification (e.g. MPEG-2) results in the value of 16 for black and the value of 235 for white when using an 8-bit representation. The standard has 8-bit digitized versions of CB and CR scaled to a different range of 16 to 240. Consequently, rescaling by the fraction (235-16)/(240-16) = 219/224 is sometimes required when doing color matrixing or processing in YCbCr space, resulting in quantization distortions when the subsequent processing is not performed using higher bit depths. The scaling that results in the use of a smaller range of digital values than what might appear to be desirable for representation of the nominal range of the input data allows for some "overshoot" and "undershoot" during processing without necessitating undesirableclipping
Clipping may refer to:
Words
* Clipping (morphology), the formation of a new word by shortening it, e.g. "ad" from "advertisement"
* Clipping (phonetics), shortening the articulation of a speech sound, usually a vowel
* Clipping (publications) ...
. This " headroom" and "toeroom" can also be used for extension of the nominal color gamut
In color reproduction, including computer graphics and photography, the gamut, or color gamut , is a certain ''complete subset'' of colors. The most common usage refers to the subset of colors which can be accurately represented in a given circ ...
, as specified by xvYCC
xvYCC or extended-gamut YCbCr is a color space that can be used in the video electronics of television sets to support a gamut 1.8 times as large as that of the sRGB color space. xvYCC was proposed by Sony, specified by the IEC in October 2005 an ...
.
The value 235 accommodates a maximum black-to-white overshoot of 255 - 235 = 20, or 20 / (235 - 16) = 9.1%, which is slightly larger than the theoretical maximum overshoot (Gibbs' Phenomenon
In mathematics, the Gibbs phenomenon, discovered by Available on-line at:National Chiao Tung University: Open Course Ware: Hewitt & Hewitt, 1979. and rediscovered by , is the Oscillation, oscillatory behavior of the Fourier series of a piecewis ...
) of about 8.9% of the maximum step. The toeroom is smaller, allowing only 16 / 219 = 7.3% overshoot, which is less than the theoretical maximum overshoot of 8.9%. But because values 0 and 255 are reserved in HDMI, it is actually slightly less.
Y'CbCr to xvYCC
Since the equations defining Y'CbCr are formed in a way that rotates the entire nominal RGB color cube and scales it to fit within a (larger) YCbCr color cube, there are some points within the Y'CbCr color cube that ''cannot'' be represented in the corresponding RGB domain (at least not within the nominal RGB range). This causes some difficulty in determining how to correctly interpret and display some Y'CbCr signals. These out-of-range Y'CbCr values are used byxvYCC
xvYCC or extended-gamut YCbCr is a color space that can be used in the video electronics of television sets to support a gamut 1.8 times as large as that of the sRGB color space. xvYCC was proposed by Sony, specified by the IEC in October 2005 an ...
to encode colors outside the BT.709 gamut.ITU-R BT.601 conversion
The form of Y′CbCr that was defined forstandard-definition television
Standard-definition television (SDTV, SD, often shortened to standard definition) is a television system which uses a resolution that is not considered to be either high or enhanced definition. "Standard" refers to it being the prevailing sp ...
use in the ITU-R
The ITU Radiocommunication Sector (ITU-R) is one of the three sectors (divisions or units) of the International Telecommunication Union (ITU) and is responsible for radio communications.
Its role is to manage the international radio-frequency sp ...
BT.601 (formerly CCIR 601
ITU-R Recommendation BT.601, more commonly known by the abbreviations Rec. 601 or BT.601 (or its former name CCIR 601) is a standard originally issued in 1982 by the Comité consultatif international pour la radio, CCIR (an organization, ...
) standard for use with digital component video
Component video is an analog video signal that has been split into two or more component channels. In popular use, it refers to a type of component analog video (CAV) information that is transmitted or stored as three separate signals. Compon ...
is derived from the corresponding RGB space (ITU-R BT.470-6 System M primaries) as follows:
:
From the above constants and formulas, the following can be derived for ITU-R BT.601.
Analog YPbPr from analog R'G'B' is derived as follows:
:
Digital Y′CbCr (8 bits per sample) is derived from analog R'G'B' as follows:
:
or simply componentwise
:
The resultant signals range from 16 to 235 for Y′ (Cb and Cr range from 16 to 240); the values from 0 to 15 are called ''footroom'', while the values from 236 to 255 are called ''headroom''.
Alternatively, digital Y′CbCr can derived from digital R'dG'dB'd (8 bits per sample, each using the full range with zero representing black and 255 representing white) according to the following equations:
:
In the formula below, the scaling factors are multiplied by . This allows for the value 256 in the denominator, which can be calculated by a single bitshift
In computer programming, a bitwise operation operates on a bit string, a bit array or a binary numeral (considered as a bit string) at the level of its individual bits. It is a fast and simple action, basic to the higher-level arithmetic operati ...
.
:
If the R'd G'd B'd digital source includes footroom and headroom, the footroom offset 16 needs to be subtracted first from each signal, and a scale factor of needs to be included in the equations.
The inverse transform is:
:
The inverse transform without any roundings (using values coming directly from ITU-R BT.601 recommendation) is:
:
This form of Y′CbCr is used primarily for older standard-definition television
Standard-definition television (SDTV, SD, often shortened to standard definition) is a television system which uses a resolution that is not considered to be either high or enhanced definition. "Standard" refers to it being the prevailing sp ...
systems, as it uses an RGB model that fits the phosphor emission characteristics of older CRTs.
ITU-R BT.709 conversion
HDTV
High-definition television (HD or HDTV) describes a television system which provides a substantially higher image resolution than the previous generation of technologies. The term has been used since 1936; in more recent times, it refers to the g ...
use. The newer form is also used in some computer-display oriented applications, as sRGB (though the matrix used for sRGB form of YCbCr, sYCC, is still BT.601). In this case, the values of Kb and Kr differ, but the formulas for using them are the same. For ITU-R BT.709, the constants are:
:
This form of Y′CbCr is based on an RGB model that more closely fits the phosphor emission characteristics of newer CRTs and other modern display equipment.
The conversion matrices for BT.709 are these:
:
The definitions of the R', G', and B' signals also differ between BT.709 and BT.601, and differ within BT.601 depending on the type of TV system in use (625-line as in PAL
Phase Alternating Line (PAL) is a colour encoding system for analogue television. It was one of three major analogue colour television standards, the others being NTSC and SECAM. In most countries it was broadcast at 625 lines, 50 fields (25 ...
and SECAM
SECAM, also written SÉCAM (, ''Séquentiel de couleur à mémoire'', French for ''color sequential with memory''), is an analog color television system that was used in France, some parts of Europe and Africa, and Russia. It was one of th ...
or 525-line as in NTSC
The first American standard for analog television broadcast was developed by National Television System Committee (NTSC)National Television System Committee (1951–1953), Report and Reports of Panel No. 11, 11-A, 12–19, with Some supplement ...
), and differ further in other specifications. In different designs there are differences in the definitions of the R, G, and B chromaticity coordinates, the reference white point, the supported gamut range, the exact gamma pre-compensation functions for deriving R', G' and B' from R, G, and B, and in the scaling and offsets to be applied during conversion from R'G'B' to Y′CbCr. So proper conversion of Y′CbCr from one form to the other is not just a matter of inverting one matrix and applying the other. In fact, when Y′CbCr is designed ideally, the values of KB and KR are derived from the precise specification of the RGB color primary signals, so that the luma (Y′) signal corresponds as closely as possible to a gamma-adjusted measurement of luminance
Luminance is a photometric measure of the luminous intensity per unit area of light travelling in a given direction. It describes the amount of light that passes through, is emitted from, or is reflected from a particular area, and falls withi ...
(typically based on the CIE 1931 measurements of the response of the human visual system to color stimuli).
ITU-R BT.2020 conversion
The ITU-R BT.2020 standard defines both BT.709 gamma corrected Y′CbCr and using the same gamma correction (except for Y', that is calculated differently), but with constant luminance Cb, Cr called YcCbcCrc. For both, the coefficients are: : The decoding matrix for BT.2020-NCL is this with 14 decimal places: : The smaller values in the matrix are not rounded, they are precise values. For systems with limited precision (8 or 10 bit, for example) a lower precision of the above matrix could be used, for example, retaining only 6 digits after decimal point. YcCbcCrc may be used when the top priority is the most accurate retention of luminance information. Color representation has true constant luminance (CL) when the luma channel (Y’ of Y′CbCr encoded with BT.709 transfer function or PQ, for example) matches with encoded luminance (BT.709 or PQ encoded luminance Y of XYZ), nevertheless YcCbcCrc does not provide for constant intensity (CI), that is done in '' ICTCP''. BT.2020 does not define PQ and thus HDR, it is further defined in SMPTE ST 2084 and BT.2100. The derivation of BT.2020 coefficients from BT.2020 primaries further changes the space.SMPTE 240M conversion
TheSMPTE 240M
The Society of Motion Picture and Television Engineers (SMPTE) (, rarely ), founded in 1916 as the Society of Motion Picture Engineers or SMPE, is a global professional association of engineers, technologists, and executives working in the m ...
standard (used on the MUSE
In ancient Greek religion and mythology, the Muses ( grc, Μοῦσαι, Moûsai, el, Μούσες, Múses) are the inspirational goddesses of literature, science, and the arts. They were considered the source of the knowledge embodied in the ...
analog HD television system) defines YCC with these coefficients:
:
The coefficients are derived from SMPTE 170M primaries and white point, as used in 240M standard.
JPEG conversion
JFIF
The JPEG File Interchange Format (JFIF) is an image file format standard published as ITU-T Recommendation T.871 and ISO/IEC 10918-5. It defines supplementary specifications for the container format that contains the image data encoded with the J ...
usage of JPEG
JPEG ( ) is a commonly used method of lossy compression for digital images, particularly for those images produced by digital photography. The degree of compression can be adjusted, allowing a selectable tradeoff between storage size and imag ...
supports a modified Rec. 601 Y′CbCr where Y′, CB and CR have the full 8-bit range of ...255 Below are the conversion equations expressed to six decimal digits of precision. (For ideal equations, see ITU-T T.871.)
Note that for the following formulae, the range of each input (R,G,B) is also the full 8-bit range of ...255
:
And back:
:
Coefficients for BT.470-6 System B, G primaries
: These coefficients are not in use and were never in use.Chromaticity-derived luminance systems
H.273 also describes constant and non-constant luminance systems which are derived strictly from primaries and white point, so that situations like sRGB/BT.709 default primaries of JPEG that use BT.601 matrix (that is derived from BT.470-6 System M) do not happen.References
External links
Y'CbCr calculator
including BT.1886
Color Space Visualization
YCbCr Definition
{{Color space Color space