Von Kármán swirling flow on:
[Wikipedia]
[Google]
[Amazon]
Von Kármán swirling flow is a flow created by a uniformly rotating infinitely long plane disk, named after
 Since there is no rotation at large , becomes independent of resulting in . Hence and .
Here the boundary conditions for the fluid are
:
:
Self-similar solution is obtained by introducing following transformation,
:
where is the fluid density.
The self-similar equations are
:
with boundary conditions for the fluid are
:
:
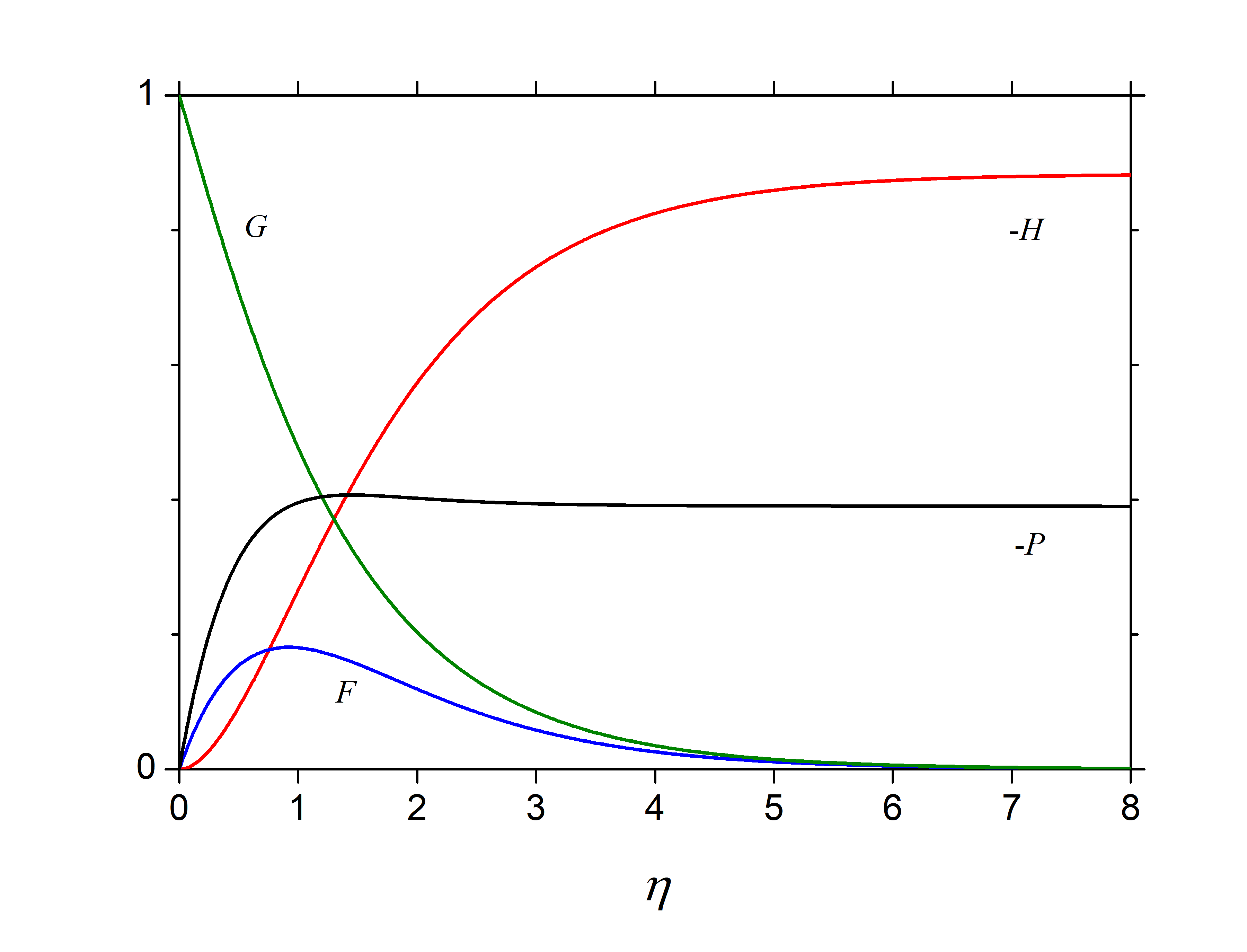
The coupled ordinary differential equations need to be solved numerically and an accurate solution is given by Cochran(1934). The inflow axial velocity at infinity obtained from the numerical integration is , so the total outflowing volume flux across a cylindrical surface of radius is . The tangential stress on the disk is . Neglecting edge effects, the torque exerted by the fluid on the disk with large () but finite radius is
:
The factor is added to account for both sides of the disk. From numerical solution, torque is given by . The torque predicted by the theory is in excellent agreement with the experiment on large disks up to the Reynolds number of about , the flow becomes turbulent at high Reynolds number.
Since there is no rotation at large , becomes independent of resulting in . Hence and .
Here the boundary conditions for the fluid are
:
:
Self-similar solution is obtained by introducing following transformation,
:
where is the fluid density.
The self-similar equations are
:
with boundary conditions for the fluid are
:
:
The coupled ordinary differential equations need to be solved numerically and an accurate solution is given by Cochran(1934). The inflow axial velocity at infinity obtained from the numerical integration is , so the total outflowing volume flux across a cylindrical surface of radius is . The tangential stress on the disk is . Neglecting edge effects, the torque exerted by the fluid on the disk with large () but finite radius is
:
The factor is added to account for both sides of the disk. From numerical solution, torque is given by . The torque predicted by the theory is in excellent agreement with the experiment on large disks up to the Reynolds number of about , the flow becomes turbulent at high Reynolds number.
Then the boundary conditions for the fluid are : : Self-similar solution is obtained by introducing following transformation, : The self-similar equations are : with boundary conditions for the fluid is : : The solution is easy to obtain only for i.e., the fluid at infinity rotates in the same sense as the plate. For , the solution is more complex, in the sense that many-solution branches occur. Evans(1969) obtained solution for the range . Zandbergen and Dijkstra showed that the solution exhibits a square root singularity as and found a second-solution branch merging with the solution found for . The solution of the second branch is continued till , at which point, a third-solution branch is found to emerge. They also discovered an infinity of solution branches around the point . Bodoyni(1975) calculated solutions for large negative , showed that the solution breaks down at . If the rotating plate is allowed to have uniform suction velocity at the plate, then meaningful solution can be obtained for . For ( represents solid body rotation, the whole fluid rotates at the same speed) the solution reaches the solid body rotation at infinity in an oscillating manner from the plate. The axial velocity is negative for and positive for . There is an explicit solution when .
Then the boundary conditions for the fluid
Theodore von Kármán
Theodore von Kármán ( hu, ( szőllőskislaki) Kármán Tódor ; born Tivadar Mihály Kármán; 11 May 18816 May 1963) was a Hungarian-American mathematician, aerospace engineer, and physicist who was active primarily in the fields of aeronaut ...
who solved the problem in 1921. The rotating disk acts as a fluid pump and is used as a model for centrifugal fans or compressors. This flow is classified under the category of steady flows in which vorticity
In continuum mechanics, vorticity is a pseudovector field that describes the local spinning motion of a continuum near some point (the tendency of something to rotate), as would be seen by an observer located at that point and traveling along wi ...
generated at a solid surface is prevented from diffusing far away by an opposing convection, the other examples being the Blasius boundary layer with suction, stagnation point flow etc.
Flow description
Consider a planar disk of infinite radius rotating at a constant angular velocity in fluid which is initially at rest everywhere. Near to the surface, the fluid is being turned by the disk, due to friction, which then causes centrifugal forces which move the fluid outwards. This outward radial motion of the fluid near the disk must be accompanied by an inward axial motion of the fluid towards the disk to conserve mass.Theodore von Kármán
Theodore von Kármán ( hu, ( szőllőskislaki) Kármán Tódor ; born Tivadar Mihály Kármán; 11 May 18816 May 1963) was a Hungarian-American mathematician, aerospace engineer, and physicist who was active primarily in the fields of aeronaut ...
noticed that the governing equations and the boundary conditions allow a solution such that and are functions of only, where are the velocity components in cylindrical coordinate with being the axis of rotation and represents the plane disk. Due to symmetry, pressure of the fluid can depend only on radial and axial coordinate .
Then the continuity equation and the incompressible Navier–Stokes equations
In physics, the Navier–Stokes equations ( ) are partial differential equations which describe the motion of viscous fluid substances, named after French engineer and physicist Claude-Louis Navier and Anglo-Irish physicist and mathematician Geo ...
reduce to
:
where is the kinematic viscosity.
No rotation at infinity
 Since there is no rotation at large , becomes independent of resulting in . Hence and .
Here the boundary conditions for the fluid are
:
:
Self-similar solution is obtained by introducing following transformation,
:
where is the fluid density.
The self-similar equations are
:
with boundary conditions for the fluid are
:
:
The coupled ordinary differential equations need to be solved numerically and an accurate solution is given by Cochran(1934). The inflow axial velocity at infinity obtained from the numerical integration is , so the total outflowing volume flux across a cylindrical surface of radius is . The tangential stress on the disk is . Neglecting edge effects, the torque exerted by the fluid on the disk with large () but finite radius is
:
The factor is added to account for both sides of the disk. From numerical solution, torque is given by . The torque predicted by the theory is in excellent agreement with the experiment on large disks up to the Reynolds number of about , the flow becomes turbulent at high Reynolds number.
Since there is no rotation at large , becomes independent of resulting in . Hence and .
Here the boundary conditions for the fluid are
:
:
Self-similar solution is obtained by introducing following transformation,
:
where is the fluid density.
The self-similar equations are
:
with boundary conditions for the fluid are
:
:
The coupled ordinary differential equations need to be solved numerically and an accurate solution is given by Cochran(1934). The inflow axial velocity at infinity obtained from the numerical integration is , so the total outflowing volume flux across a cylindrical surface of radius is . The tangential stress on the disk is . Neglecting edge effects, the torque exerted by the fluid on the disk with large () but finite radius is
:
The factor is added to account for both sides of the disk. From numerical solution, torque is given by . The torque predicted by the theory is in excellent agreement with the experiment on large disks up to the Reynolds number of about , the flow becomes turbulent at high Reynolds number.
Rigid body rotation at infinity
This problem was addressed by George Keith Batchelor(1951). Let be the angular velocity at infinity. Now the pressure at is . Hence and .Then the boundary conditions for the fluid are : : Self-similar solution is obtained by introducing following transformation, : The self-similar equations are : with boundary conditions for the fluid is : : The solution is easy to obtain only for i.e., the fluid at infinity rotates in the same sense as the plate. For , the solution is more complex, in the sense that many-solution branches occur. Evans(1969) obtained solution for the range . Zandbergen and Dijkstra showed that the solution exhibits a square root singularity as and found a second-solution branch merging with the solution found for . The solution of the second branch is continued till , at which point, a third-solution branch is found to emerge. They also discovered an infinity of solution branches around the point . Bodoyni(1975) calculated solutions for large negative , showed that the solution breaks down at . If the rotating plate is allowed to have uniform suction velocity at the plate, then meaningful solution can be obtained for . For ( represents solid body rotation, the whole fluid rotates at the same speed) the solution reaches the solid body rotation at infinity in an oscillating manner from the plate. The axial velocity is negative for and positive for . There is an explicit solution when .
Nearly rotating at the same speed,
Since both boundary conditions for are almost equal to one, one would expect the solution for to slightly deviate from unity. The corresponding scales for and can be derived from the self-similar equations. Therefore, : To the first order approximation(neglecting ), the self-similar equation becomes : with exact solutions : These solution are similar to anEkman layer
The Ekman layer is the layer in a fluid where there is a force balance between pressure gradient force, Coriolis force and turbulent drag. It was first described by Vagn Walfrid Ekman. Ekman layers occur both in the atmosphere and in the ocean ...
solution.
Non-Axisymmetric solutions
The flow accepts a non-axisymmetric solution with axisymmetric boundary conditions discovered by Hewitt, Duck and Foster. Defining and the governing equations are : with boundary conditions : The solution is found to exist from numerical integration for .Bödewadt flow
Bödewadt flow describes the flow when a stationary disk is placed in a rotating fluid.Two rotating coaxial disks
This problem was addressed by George Keith Batchelor(1951),Keith Stewartson
Keith Stewartson (20 September 1925 – 7 May 1983) was an English mathematician and fellow of the Royal Society.
Early life
The youngest of three children, Stewartson was born to an English baker in 1925. He was raised in Billingham, County Dur ...
(1952) and many other researchers. Here the solution is not simple, because of the additional length scale imposed in the problem i.e., the distance between the two disks. In addition, the uniqueness and existence of a steady solution are also depend on the corresponding Reynolds number .Then the boundary conditions for the fluid