Spring pendulum on:
[Wikipedia]
[Google]
[Amazon]
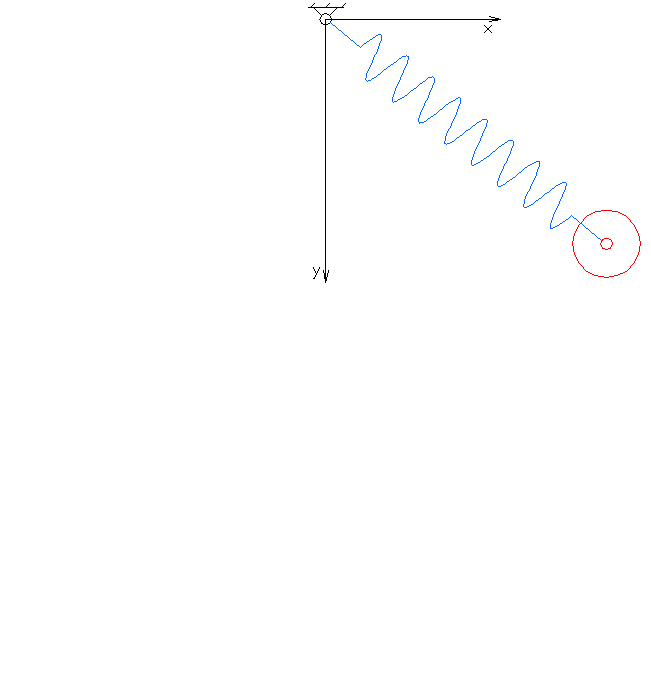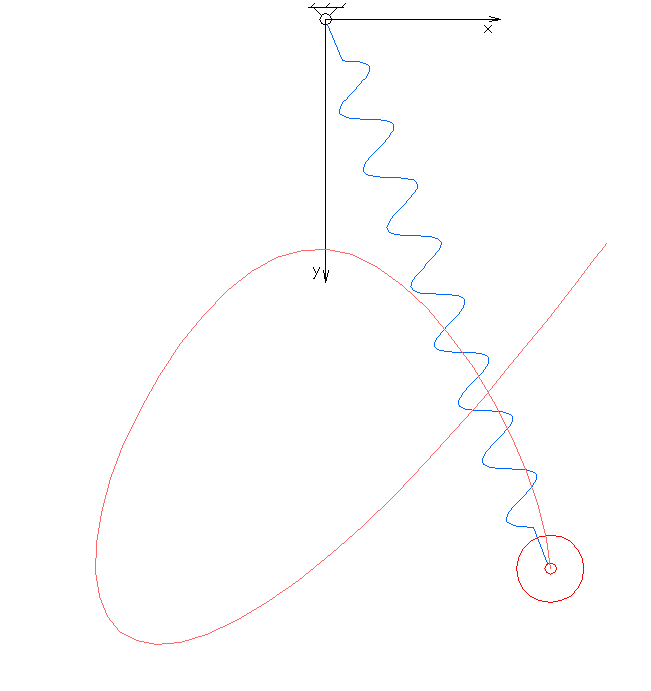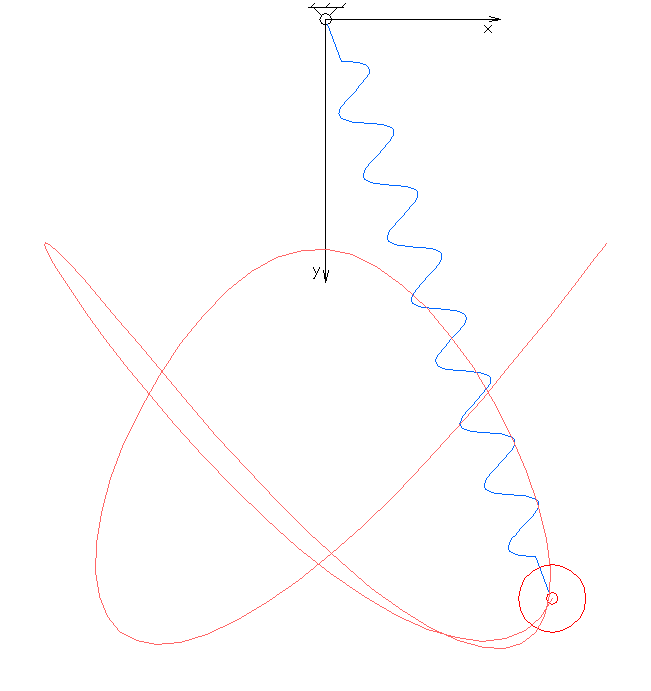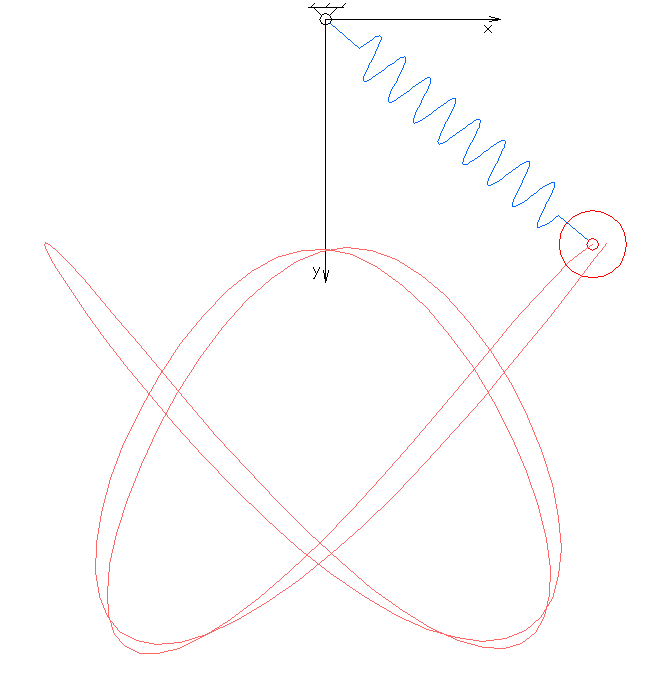 In
In
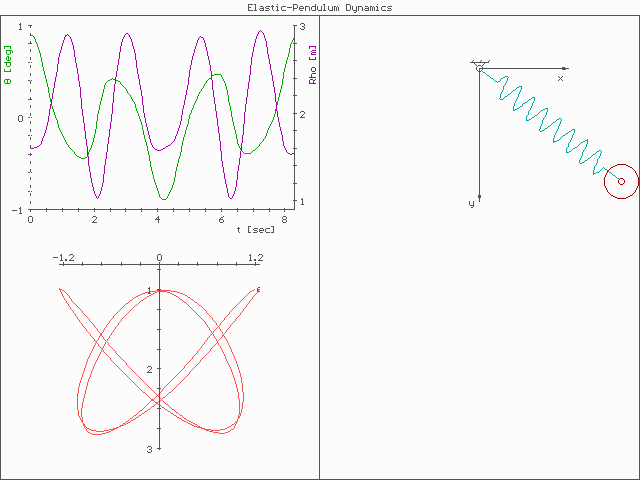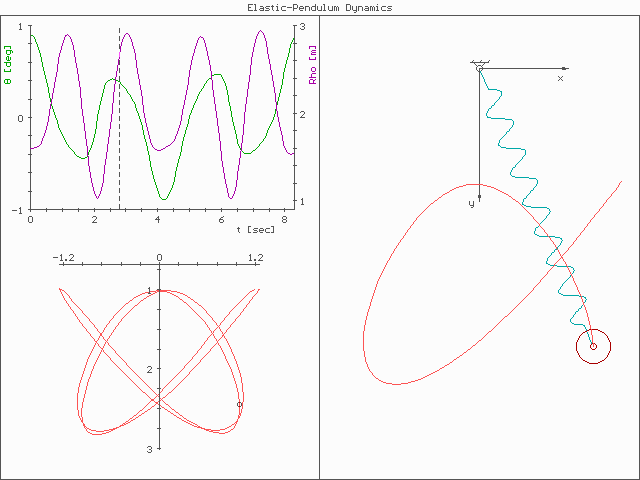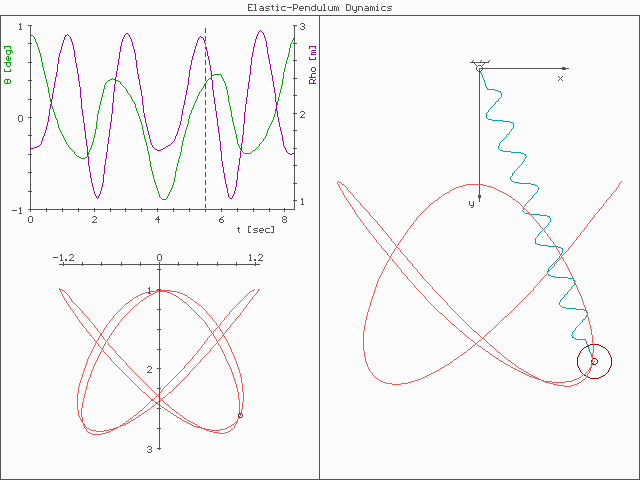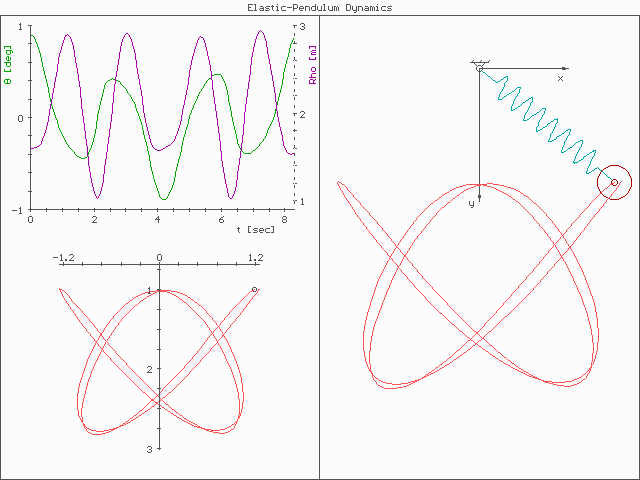 The system is much more complex than a simple pendulum, as the properties of the spring add an extra dimension of freedom to the system. For example, when the spring compresses, the shorter radius causes the spring to move faster due to the conservation of
The system is much more complex than a simple pendulum, as the properties of the spring add an extra dimension of freedom to the system. For example, when the spring compresses, the shorter radius causes the spring to move faster due to the conservation of
"Oscillations of an elastic pendulum"
(interactive animation), Wolfram Demonstrations Project, published February 19, 2019. {{Chaos theory Chaotic maps Dynamical systems Mathematical physics Pendulums
 In
In physics
Physics is the natural science that studies matter, its fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge which r ...
and mathematics, in the area of dynamical systems, an elastic pendulum (also called spring pendulum or swinging spring) is a physical system where a piece of mass is connected to a spring
Spring(s) may refer to:
Common uses
* Spring (season)
Spring, also known as springtime, is one of the four temperate seasons, succeeding winter and preceding summer. There are various technical definitions of spring, but local usage of ...
so that the resulting motion contains elements of both a simple pendulum
A pendulum is a weight suspended from a pivot so that it can swing freely. When a pendulum is displaced sideways from its resting, equilibrium position, it is subject to a restoring force due to gravity that will accelerate it back toward th ...
and a one-dimensional
In physics and mathematics, a sequence of ''n'' numbers can specify a location in ''n''-dimensional space. When , the set of all such locations is called a one-dimensional space. An example of a one-dimensional space is the number line, where the ...
spring-mass system
In classical mechanics, a harmonic oscillator is a system that, when displaced from its equilibrium position, experiences a restoring force ''F'' proportional to the displacement ''x'':
\vec F = -k \vec x,
where ''k'' is a positive consta ...
. The system exhibits chaotic behaviour and is sensitive to initial conditions
In mathematics and particularly in dynamic systems, an initial condition, in some contexts called a seed value, is a value of an evolving variable at some point in time designated as the initial time (typically denoted ''t'' = 0). For ...
. The motion of an elastic pendulum is governed by a set of coupled ordinary differential equation
In mathematics, an ordinary differential equation (ODE) is a differential equation whose unknown(s) consists of one (or more) function(s) of one variable and involves the derivatives of those functions. The term ''ordinary'' is used in contrast ...
s.
Analysis and interpretation
 The system is much more complex than a simple pendulum, as the properties of the spring add an extra dimension of freedom to the system. For example, when the spring compresses, the shorter radius causes the spring to move faster due to the conservation of
The system is much more complex than a simple pendulum, as the properties of the spring add an extra dimension of freedom to the system. For example, when the spring compresses, the shorter radius causes the spring to move faster due to the conservation of angular momentum
In physics, angular momentum (rarely, moment of momentum or rotational momentum) is the rotational analog of linear momentum. It is an important physical quantity because it is a conserved quantity—the total angular momentum of a closed syst ...
. It is also possible that the spring has a range that is overtaken by the motion of the pendulum, making it practically neutral to the motion of the pendulum.
Lagrangian
The spring has the rest length and can be stretched by a length . The angle of oscillation of the pendulum is . TheLagrangian
Lagrangian may refer to:
Mathematics
* Lagrangian function, used to solve constrained minimization problems in optimization theory; see Lagrange multiplier
** Lagrangian relaxation, the method of approximating a difficult constrained problem with ...
is:
:
where is the kinetic energy
In physics, the kinetic energy of an object is the energy that it possesses due to its motion.
It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acc ...
and is the potential energy.
See. Hooke's law
In physics, Hooke's law is an empirical law which states that the force () needed to extend or compress a spring by some distance () scales linearly with respect to that distance—that is, where is a constant factor characteristic of ...
is the potential energy of the spring itself:
:
where is the spring constant.
The potential energy from gravity
In physics, gravity () is a fundamental interaction which causes mutual attraction between all things with mass or energy. Gravity is, by far, the weakest of the four fundamental interactions, approximately 1038 times weaker than the stro ...
, on the other hand, is determined by the height of the mass. For a given angle and displacement, the potential energy is:
:
where is the gravitational acceleration
In physics, gravitational acceleration is the acceleration of an object in free fall within a vacuum (and thus without experiencing drag). This is the steady gain in speed caused exclusively by the force of gravitational attraction. All bodi ...
.
The kinetic energy is given by:
:
where is the velocity
Velocity is the directional speed of an object in motion as an indication of its rate of change in position as observed from a particular frame of reference and as measured by a particular standard of time (e.g. northbound). Velocity i ...
of the mass. To relate to the other variables, the velocity is written as a combination of a movement along and perpendicular to the spring:
:
So the Lagrangian becomes:
:
:
Equations of motion
With two degrees of freedom, for and , the equations of motion can be found using two Euler-Lagrange equations: : : For : : isolated: : And for : : isolated: : The elastic pendulum is now described with two coupled ordinary differential equations. These can be solved numerically. Furthermore, one can use analytical methods to study the intriguing phenomenon of order-chaos-order in this system.See also
* Double pendulum *Duffing oscillator
The Duffing equation (or Duffing oscillator), named after Georg Duffing (1861–1944), is a non-linear second-order differential equation used to model certain damped and driven oscillators. The equation is given by
:\ddot + \delta \dot + \a ...
* Pendulum (mathematics)
* Spring-mass system
In classical mechanics, a harmonic oscillator is a system that, when displaced from its equilibrium position, experiences a restoring force ''F'' proportional to the displacement ''x'':
\vec F = -k \vec x,
where ''k'' is a positive consta ...
References
Further reading
* *External links
* Holovatsky V., Holovatska Y. (2019"Oscillations of an elastic pendulum"
(interactive animation), Wolfram Demonstrations Project, published February 19, 2019. {{Chaos theory Chaotic maps Dynamical systems Mathematical physics Pendulums