Sine function on:
[Wikipedia]
[Google]
[Amazon]
In mathematics, sine and cosine are
 To define the sine and cosine of an acute angle ''α'', start with a
To define the sine and cosine of an acute angle ''α'', start with a
 Let a line through the origin intersect the unit circle, making an angle of ''θ'' with the positive half of the ''x''-axis. The ''x''- and ''y''-coordinates of this point of intersection are equal to and , respectively. This definition is consistent with the right-angled triangle definition of sine and cosine when : because the length of the hypotenuse of the unit circle is always 1, . The length of the opposite side of the triangle is simply the ''y''-coordinate. A similar argument can be made for the cosine function to show that when , even under the new definition using the unit circle. is then defined as , or, equivalently, as the slope of the line segment.
Using the unit circle definition has the advantage that the angle can be extended to any real argument. This can also be achieved by requiring certain symmetries, and that sine be a
Let a line through the origin intersect the unit circle, making an angle of ''θ'' with the positive half of the ''x''-axis. The ''x''- and ''y''-coordinates of this point of intersection are equal to and , respectively. This definition is consistent with the right-angled triangle definition of sine and cosine when : because the length of the hypotenuse of the unit circle is always 1, . The length of the opposite side of the triangle is simply the ''y''-coordinate. A similar argument can be made for the cosine function to show that when , even under the new definition using the unit circle. is then defined as , or, equivalently, as the slope of the line segment.
Using the unit circle definition has the advantage that the angle can be extended to any real argument. This can also be achieved by requiring certain symmetries, and that sine be a
File:Circle cos sin.gif, Animation showing how the sine function (in red) is graphed from the ''y''-coordinate (red dot) of a point on the
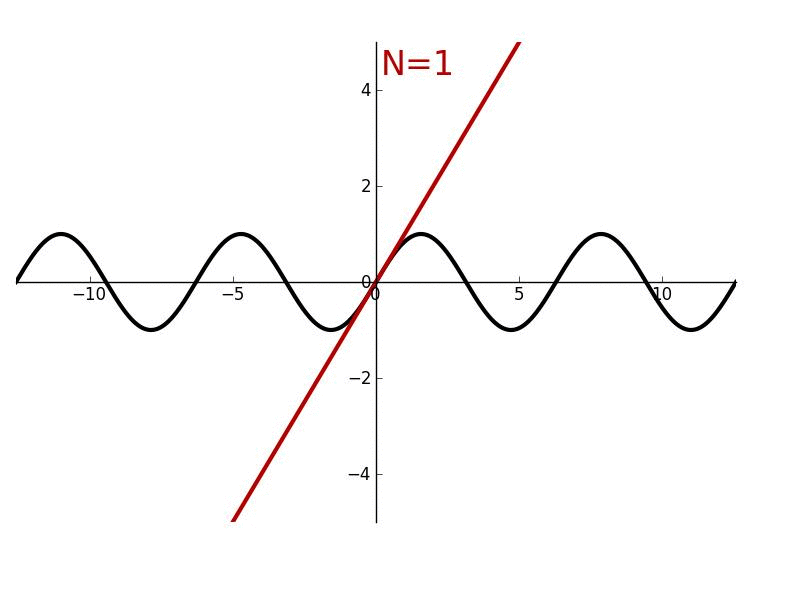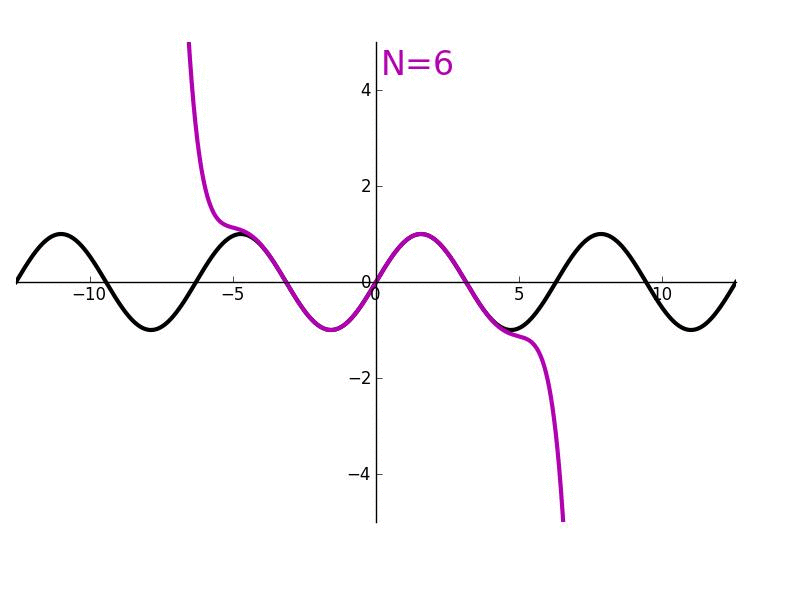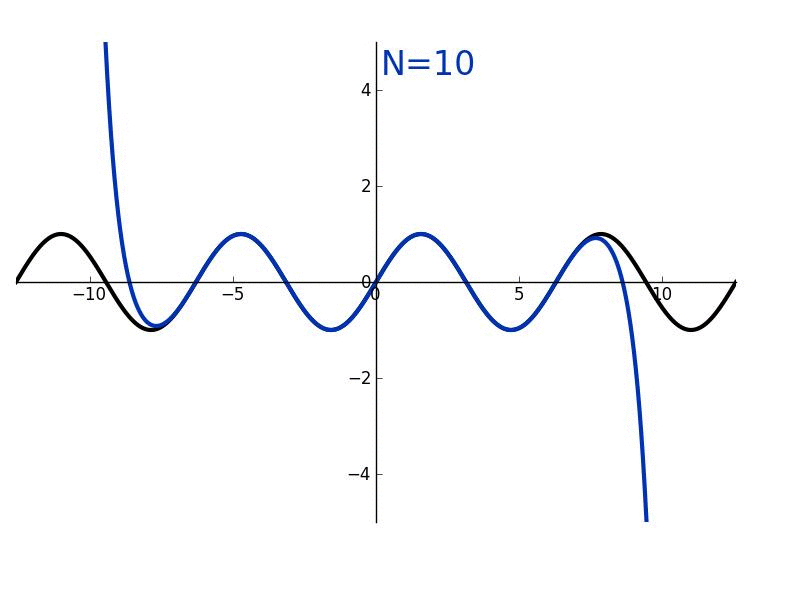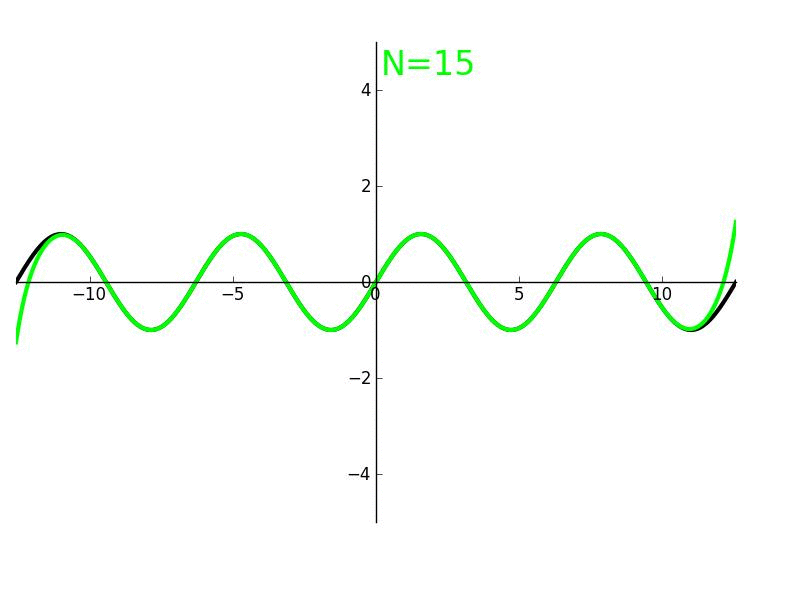 The successive derivatives of sine, evaluated at zero, can be used to determine its Taylor series. Using only geometry and properties of
The successive derivatives of sine, evaluated at zero, can be used to determine its Taylor series. Using only geometry and properties of
 The
The
 The cosine double angle formula implies that sin2 and cos2 are, themselves, shifted and scaled sine waves. Specifically,
:
The graph shows both the sine function and the sine squared function, with the sine in blue and sine squared in red. Both graphs have the same shape, but with different ranges of values, and different periods. Sine squared has only positive values, but twice the number of periods.
The cosine double angle formula implies that sin2 and cos2 are, themselves, shifted and scaled sine waves. Specifically,
:
The graph shows both the sine function and the sine squared function, with the sine in blue and sine squared in red. Both graphs have the same shape, but with different ranges of values, and different periods. Sine squared has only positive values, but twice the number of periods.
 The table below displays many of the key properties of the sine function (sign, monotonicity, convexity), arranged by the quadrant of the argument. For arguments outside those in the table, one may compute the corresponding information by using the periodicity of the sine function.
The table below displays many of the key properties of the sine function (sign, monotonicity, convexity), arranged by the quadrant of the argument. For arguments outside those in the table, one may compute the corresponding information by using the periodicity of the sine function.
 The following table gives basic information at the boundary of the quadrants.
The following table gives basic information at the boundary of the quadrants.
 Sine and cosine are used to connect the real and imaginary parts of a
Sine and cosine are used to connect the real and imaginary parts of a

 Applying the series definition of the sine and cosine to a complex argument, ''z'', gives:
:
where sinh and cosh are the hyperbolic sine and cosine. These are
Applying the series definition of the sine and cosine to a complex argument, ''z'', gives:
:
where sinh and cosh are the hyperbolic sine and cosine. These are
 While the early study of trigonometry can be traced to antiquity, the
While the early study of trigonometry can be traced to antiquity, the
See
See Maor (1998), chapter 3, regarding the etymology.), due to visual similarity between the arc of a circle with its corresponding chord and a bow with its string (see
/ref>R Documentation sinpi
/ref> In MATLAB, OpenCL, R, Julia, CUDA, and ARM, these function are calledALLEGRO Angle Sensor Datasheet
/ref> If half-turns are used as the unit for angle, then the value provided by the sensor directly and losslessly maps to a fixed-point data type with 11 bits to the right of the binary point. In contrast, if radians are used as the unit for storing the angle, then the inaccuracies and cost of multiplying the raw sensor integer by an approximation to would be incurred.
trigonometric function
In mathematics, the trigonometric functions (also called circular functions, angle functions or goniometric functions) are real functions which relate an angle of a right-angled triangle to ratios of two side lengths. They are widely used in a ...
s of an angle
In Euclidean geometry, an angle is the figure formed by two rays, called the '' sides'' of the angle, sharing a common endpoint, called the '' vertex'' of the angle.
Angles formed by two rays lie in the plane that contains the rays. Angles a ...
. The sine and cosine of an acute angle
In Euclidean geometry, an angle is the figure formed by two rays, called the '' sides'' of the angle, sharing a common endpoint, called the '' vertex'' of the angle.
Angles formed by two rays lie in the plane that contains the rays. Angles a ...
are defined in the context of a right triangle
A right triangle (American English) or right-angled triangle ( British), or more formally an orthogonal triangle, formerly called a rectangled triangle ( grc, ὀρθόσγωνία, lit=upright angle), is a triangle in which one angle is a right a ...
: for the specified angle, its sine is the ratio of the length of the side that is opposite that angle to the length of the longest side of the triangle
A triangle is a polygon with three edges and three vertices. It is one of the basic shapes in geometry. A triangle with vertices ''A'', ''B'', and ''C'' is denoted \triangle ABC.
In Euclidean geometry, any three points, when non- colline ...
(the hypotenuse
In geometry, a hypotenuse is the longest side of a right-angled triangle, the side opposite the right angle. The length of the hypotenuse can be found using the Pythagorean theorem, which states that the square of the length of the hypotenuse e ...
), and the cosine is the ratio
In mathematics, a ratio shows how many times one number contains another. For example, if there are eight oranges and six lemons in a bowl of fruit, then the ratio of oranges to lemons is eight to six (that is, 8:6, which is equivalent to the ...
of the length of the adjacent leg to that of the hypotenuse
In geometry, a hypotenuse is the longest side of a right-angled triangle, the side opposite the right angle. The length of the hypotenuse can be found using the Pythagorean theorem, which states that the square of the length of the hypotenuse e ...
. For an angle , the sine and cosine functions are denoted simply as and .
More generally, the definitions of sine and cosine can be extended to any real
Real may refer to:
Currencies
* Brazilian real (R$)
* Central American Republic real
* Mexican real
* Portuguese real
* Spanish real
* Spanish colonial real
Music Albums
* ''Real'' (L'Arc-en-Ciel album) (2000)
* ''Real'' (Bright album) (2010) ...
value in terms of the lengths of certain line segments in a unit circle
In mathematics, a unit circle is a circle of unit radius—that is, a radius of 1. Frequently, especially in trigonometry, the unit circle is the circle of radius 1 centered at the origin (0, 0) in the Cartesian coordinate system in the Eucli ...
. More modern definitions express the sine and cosine as infinite series
In mathematics, a series is, roughly speaking, a description of the operation of adding infinitely many quantities, one after the other, to a given starting quantity. The study of series is a major part of calculus and its generalization, math ...
, or as the solutions of certain differential equation
In mathematics, a differential equation is an equation that relates one or more unknown functions and their derivatives. In applications, the functions generally represent physical quantities, the derivatives represent their rates of change, an ...
s, allowing their extension to arbitrary positive and negative values and even to complex number
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the fo ...
s.
The sine and cosine functions are commonly used to model periodic phenomena such as sound
In physics, sound is a vibration that propagates as an acoustic wave, through a transmission medium such as a gas, liquid or solid.
In human physiology and psychology, sound is the ''reception'' of such waves and their ''perception'' b ...
and light waves, the position and velocity of harmonic oscillators, sunlight intensity and day length, and average temperature variations throughout the year. They can be traced to the and functions used in Indian astronomy
Astronomy has long history in Indian subcontinent stretching from pre-historic to modern times. Some of the earliest roots of Indian astronomy can be dated to the period of Indus Valley civilisation or earlier. Astronomy later developed as a dis ...
during the Gupta period
The Gupta Empire was an ancient Indian empire which existed from the early 4th century CE to late 6th century CE. At its zenith, from approximately 319 to 467 CE, it covered much of the Indian subcontinent. This period is considered as the Gold ...
.
Notation
Sine and cosine are written usingfunctional notation
In mathematics, a function from a set to a set assigns to each element of exactly one element of .; the words map, mapping, transformation, correspondence, and operator are often used synonymously. The set is called the domain of the functi ...
with the abbreviations ''sin'' and ''cos''.
Often, if the argument is simple enough, the function value will be written without parentheses, as rather than as .
Each of sine and cosine is a function of an angle, which is usually expressed in terms of radian
The radian, denoted by the symbol rad, is the unit of angle in the International System of Units (SI) and is the standard unit of angular measure used in many areas of mathematics. The unit was formerly an SI supplementary unit (before tha ...
s or degrees. Except where explicitly stated otherwise, this article assumes that the angle is measured in radians.
Definitions
Right-angled triangle definitions
right triangle
A right triangle (American English) or right-angled triangle ( British), or more formally an orthogonal triangle, formerly called a rectangled triangle ( grc, ὀρθόσγωνία, lit=upright angle), is a triangle in which one angle is a right a ...
that contains an angle of measure ''α''; in the accompanying figure, angle ''α'' in triangle ''ABC'' is the angle of interest. The three sides of the triangle are named as follows:
* The ''opposite side'' is the side opposite to the angle of interest, in this case side ''a''.
* The ''hypotenuse'' is the side opposite the right angle, in this case side ''h''. The hypotenuse is always the longest side of a right-angled triangle.
* The ''adjacent side'' is the remaining side, in this case side ''b''. It forms a side of (and is adjacent to) both the angle of interest (angle ''A'') and the right angle.
Once such a triangle is chosen, the sine of the angle is equal to the length of the opposite side, divided by the length of the hypotenuse:
:
The other trigonometric functions of the angle can be defined similarly; for example, the tangent
In geometry, the tangent line (or simply tangent) to a plane curve at a given point is the straight line that "just touches" the curve at that point. Leibniz defined it as the line through a pair of infinitely close points on the curve. Mo ...
is the ratio between the opposite and adjacent sides.
As stated, the values and appear to depend on the choice of right triangle containing an angle of measure ''α''. However, this is not the case: all such triangles are similar, and so the ratios are the same for each of them.
Unit circle definitions
Intrigonometry
Trigonometry () is a branch of mathematics that studies relationships between side lengths and angles of triangles. The field emerged in the Hellenistic world during the 3rd century BC from applications of geometry to astronomical studies ...
, a unit circle
In mathematics, a unit circle is a circle of unit radius—that is, a radius of 1. Frequently, especially in trigonometry, the unit circle is the circle of radius 1 centered at the origin (0, 0) in the Cartesian coordinate system in the Eucli ...
is the circle of radius one centered at the origin (0, 0) in the Cartesian coordinate system.
periodic function
A periodic function is a function that repeats its values at regular intervals. For example, the trigonometric functions, which repeat at intervals of 2\pi radians, are periodic functions. Periodic functions are used throughout science to des ...
.
Complex exponential function definitions
Theexponential function
The exponential function is a mathematical function denoted by f(x)=\exp(x) or e^x (where the argument is written as an exponent). Unless otherwise specified, the term generally refers to the positive-valued function of a real variable, ...
is defined on the entire domain of the complex numbers
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the form ...
. The definition of sine and cosine can be extended to all complex numbers via
:
:
These can be reversed to give Euler's formula
Euler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the fundamental relationship between the trigonometric functions and the complex exponential function. Euler's formula states that fo ...
:
:
When plotted on the complex plane, the function for real values of traces out the unit circle
In mathematics, a unit circle is a circle of unit radius—that is, a radius of 1. Frequently, especially in trigonometry, the unit circle is the circle of radius 1 centered at the origin (0, 0) in the Cartesian coordinate system in the Eucli ...
in the complex plane.
When is a real number sine and cosine simplify to the imaginary and real parts of or , as:
:
:
When for real values and , sine and cosine can be expressed in terms of real sines, cosines, and hyperbolic function
In mathematics, hyperbolic functions are analogues of the ordinary trigonometric functions, but defined using the hyperbola rather than the circle. Just as the points form a circle with a unit radius, the points form the right half of the u ...
s as
:
Differential equation definition
is the solution to the two-dimensional system ofdifferential equation
In mathematics, a differential equation is an equation that relates one or more unknown functions and their derivatives. In applications, the functions generally represent physical quantities, the derivatives represent their rates of change, an ...
s and with the initial conditions
In mathematics and particularly in dynamic systems, an initial condition, in some contexts called a seed value, is a value of an evolving variable at some point in time designated as the initial time (typically denoted ''t'' = 0). For ...
and . One could interpret the unit circle in the above definitions as defining the phase space trajectory of the differential equation with the given initial conditions.
unit circle
In mathematics, a unit circle is a circle of unit radius—that is, a radius of 1. Frequently, especially in trigonometry, the unit circle is the circle of radius 1 centered at the origin (0, 0) in the Cartesian coordinate system in the Eucli ...
(in green), at an angle of ''θ''. The cosine (in blue) is the ''x''-coordinate. It can be interpreted as a phase space trajectory of the system of differential equations and starting from the initial conditions and .
Series definitions
 The successive derivatives of sine, evaluated at zero, can be used to determine its Taylor series. Using only geometry and properties of
The successive derivatives of sine, evaluated at zero, can be used to determine its Taylor series. Using only geometry and properties of limits
Limit or Limits may refer to:
Arts and media
* ''Limit'' (manga), a manga by Keiko Suenobu
* ''Limit'' (film), a South Korean film
* Limit (music), a way to characterize harmony
* "Limit" (song), a 2016 single by Luna Sea
* "Limits", a 2019 ...
, it can be shown that the derivative
In mathematics, the derivative of a function of a real variable measures the sensitivity to change of the function value (output value) with respect to a change in its argument (input value). Derivatives are a fundamental tool of calculus. ...
of sine is cosine, and that the derivative of cosine is the negative of sine. This means the successive derivatives of sin(x) are cos(x), -sin(x), -cos(x), sin(x), continuing to repeat those four functions. The (4''n''+''k'')-th derivative, evaluated at the point 0:
:
where the superscript represents repeated differentiation. This implies the following Taylor series expansion at x = 0. One can then use the theory of Taylor series
In mathematics, the Taylor series or Taylor expansion of a function is an infinite sum of terms that are expressed in terms of the function's derivatives at a single point. For most common functions, the function and the sum of its Taylor ser ...
to show that the following identities hold for all real number
In mathematics, a real number is a number that can be used to measure a ''continuous'' one-dimensional quantity such as a distance, duration or temperature. Here, ''continuous'' means that values can have arbitrarily small variations. Every ...
s ''x'' (where x is the angle in radians):
:
Taking the derivative of each term gives the Taylor series for cosine:
:
Continued fraction definitions
The sine function can also be represented as ageneralized continued fraction In complex analysis, a branch of mathematics, a generalized continued fraction is a generalization of regular continued fractions in canonical form, in which the partial numerators and partial denominators can assume arbitrary complex values.
A ge ...
:
:
:
The continued fraction representations can be derived from Euler's continued fraction formula
In the analytic theory of continued fractions, Euler's continued fraction formula is an identity connecting a certain very general infinite series with an infinite continued fraction. First published in 1748, it was at first regarded as a simple ...
and express the real number
In mathematics, a real number is a number that can be used to measure a ''continuous'' one-dimensional quantity such as a distance, duration or temperature. Here, ''continuous'' means that values can have arbitrarily small variations. Every ...
values, both rational
Rationality is the quality of being guided by or based on reasons. In this regard, a person acts rationally if they have a good reason for what they do or a belief is rational if it is based on strong evidence. This quality can apply to an abi ...
and irrational
Irrationality is cognition, thinking, talking, or acting without inclusion of rationality. It is more specifically described as an action or opinion given through inadequate use of reason, or through emotional distress or cognitive deficiency. T ...
, of the sine and cosine functions.
Identities
Exact identities (usingradian
The radian, denoted by the symbol rad, is the unit of angle in the International System of Units (SI) and is the standard unit of angular measure used in many areas of mathematics. The unit was formerly an SI supplementary unit (before tha ...
s):
These apply for all values of .
:
:
Reciprocals
Thereciprocal
Reciprocal may refer to:
In mathematics
* Multiplicative inverse, in mathematics, the number 1/''x'', which multiplied by ''x'' gives the product 1, also known as a ''reciprocal''
* Reciprocal polynomial, a polynomial obtained from another pol ...
of sine is cosecant, i.e., the reciprocal of is , or . Cosecant gives the ratio of the length of the hypotenuse to the length of the opposite side. Similarly, the reciprocal of cosine is secant, which gives the ratio of the length of the hypotenuse to that of the adjacent side.
:
:
Inverses
inverse function
In mathematics, the inverse function of a function (also called the inverse of ) is a function that undoes the operation of . The inverse of exists if and only if is bijective, and if it exists, is denoted by f^ .
For a function f\colon X ...
of sine is arcsine (arcsin or asin) or inverse sine (). The inverse function of cosine is arccosine (arccos, acos, or ). (The superscript of −1 in and denotes the inverse of a function, not exponentiation
Exponentiation is a mathematical operation, written as , involving two numbers, the '' base'' and the ''exponent'' or ''power'' , and pronounced as " (raised) to the (power of) ". When is a positive integer, exponentiation corresponds to r ...
.) As sine and cosine are not injective, their inverses are not exact inverse functions, but partial inverse functions. For example, , but also , etc. It follows that the arcsine function is multivalued: , but also , , etc. When only one value is desired, the function may be restricted to its principal branch In mathematics, a principal branch is a function which selects one branch ("slice") of a multi-valued function. Most often, this applies to functions defined on the complex plane.
Examples
Trigonometric inverses
Principal branches are use ...
. With this restriction, for each ''x'' in the domain, the expression will evaluate only to a single value, called its principal value. The standard range of principal values for arcsin is from to and the standard range for arccos is from to .
:
where (for some integer ''k''):
:
By definition, arcsin and arccos satisfy the equations:
:
and
:
Pythagorean trigonometric identity
The basic relationship between the sine and the cosine is the Pythagorean trigonometric identity: : where sin2(''x'') means (sin(''x''))2.Double angle formulas
Sine and cosine satisfy the following double angle formulas: : : The cosine double angle formula implies that sin2 and cos2 are, themselves, shifted and scaled sine waves. Specifically,
:
The graph shows both the sine function and the sine squared function, with the sine in blue and sine squared in red. Both graphs have the same shape, but with different ranges of values, and different periods. Sine squared has only positive values, but twice the number of periods.
The cosine double angle formula implies that sin2 and cos2 are, themselves, shifted and scaled sine waves. Specifically,
:
The graph shows both the sine function and the sine squared function, with the sine in blue and sine squared in red. Both graphs have the same shape, but with different ranges of values, and different periods. Sine squared has only positive values, but twice the number of periods.
Derivative and integrals
The derivatives of sine and cosine are: : and their antiderivatives are: : : where ''C'' denotes theconstant of integration
In calculus, the constant of integration, often denoted by C (or c), is a constant term added to an antiderivative of a function f(x) to indicate that the indefinite integral of f(x) (i.e., the set of all antiderivatives of f(x)), on a connected ...
.
Properties relating to the quadrants
Fixed points
The fixed point iteration ''x''''n''+1 = cos(''xn'') with initial value ''x''0 = −1 converges to the Dottie number. Zero is the only real fixed point of the sine function; in other words the only intersection of the sine function and theidentity function
Graph of the identity function on the real numbers
In mathematics, an identity function, also called an identity relation, identity map or identity transformation, is a function that always returns the value that was used as its argument, un ...
is . The only real fixed point of the cosine function is called the Dottie number
The Dottie number is the unique real fixed point of the cosine function.
In mathematics, the Dottie number is a constant that is the unique real root of the equation
: \cos x = x ,
where the argument of \cos is in radians. The decimal expan ...
. That is, the Dottie number is the unique real root of the equation The decimal expansion of the Dottie number is .
Arc length
Thearc length
ARC may refer to:
Business
* Aircraft Radio Corporation, a major avionics manufacturer from the 1920s to the '50s
* Airlines Reporting Corporation, an airline-owned company that provides ticket distribution, reporting, and settlement services
* ...
of the sine curve between and is
:
where is the incomplete elliptic integral of the second kind with modulus . It cannot be expressed using elementary function
In mathematics, an elementary function is a function of a single variable (typically real or complex) that is defined as taking sums, products, roots and compositions of finitely many polynomial, rational, trigonometric, hyperbolic, and ...
s.
The arc length for a full period is
:
where is the gamma function
In mathematics, the gamma function (represented by , the capital letter gamma from the Greek alphabet) is one commonly used extension of the factorial function to complex numbers. The gamma function is defined for all complex numbers except ...
and is the lemniscate constant
In mathematics, the lemniscate constant p. 199 is a transcendental mathematical constant that is the ratio of the perimeter of Bernoulli's lemniscate to its diameter, analogous to the definition of for the circle. Equivalently, the perimeter ...
.
Law of sines
Thelaw of sines
In trigonometry, the law of sines, sine law, sine formula, or sine rule is an equation relating the lengths of the sides of any triangle to the sines of its angles. According to the law,
\frac \,=\, \frac \,=\, \frac \,=\, 2R,
where , and ar ...
states that for an arbitrary triangle with sides ''a'', ''b'', and ''c'' and angles opposite those sides ''A'', ''B'' and ''C'':
:
This is equivalent to the equality of the first three expressions below:
:
where ''R'' is the triangle's circumradius
In geometry, the circumscribed circle or circumcircle of a polygon is a circle that passes through all the vertices of the polygon. The center of this circle is called the circumcenter and its radius is called the circumradius.
Not every polyg ...
.
It can be proved by dividing the triangle into two right ones and using the above definition of sine. The law of sines is useful for computing the lengths of the unknown sides in a triangle if two angles and one side are known. This is a common situation occurring in '' triangulation'', a technique to determine unknown distances by measuring two angles and an accessible enclosed distance.
Law of cosines
Thelaw of cosines
In trigonometry, the law of cosines (also known as the cosine formula, cosine rule, or al-Kashi's theorem) relates the lengths of the sides of a triangle to the cosine of one of its angles. Using notation as in Fig. 1, the law of cosines states ...
states that for an arbitrary triangle with sides ''a'', ''b'', and ''c'' and angles opposite those sides ''A'', ''B'' and ''C'':
:
In the case where , and this becomes the Pythagorean theorem: for a right triangle, where ''c'' is the hypotenuse.
Special values
For certain integral numbers ''x'' of degrees, the values of sin(''x'') and cos(''x'') are particularly simple and can be expressed without nested square roots. A table of these angles is given below. For more complex angle expressions see . 90 degree increments:Relationship to complex numbers
complex number
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the fo ...
with its polar coordinates
In mathematics, the polar coordinate system is a two-dimensional coordinate system in which each point on a plane is determined by a distance from a reference point and an angle from a reference direction. The reference point (analogous to th ...
(''r'', ''φ''):
:
The real and imaginary parts are:
:
:
where ''r'' and ''φ'' represent the magnitude and angle of the complex number ''z''.
For any real number ''θ'', Euler's formula
Euler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the fundamental relationship between the trigonometric functions and the complex exponential function. Euler's formula states that fo ...
says that:
:
Therefore, if the polar coordinates of ''z'' are (''r'', ''φ''),
Complex arguments

entire function
In complex analysis, an entire function, also called an integral function, is a complex-valued function that is holomorphic on the whole complex plane. Typical examples of entire functions are polynomials and the exponential function, and any fin ...
s.
It is also sometimes useful to express the complex sine and cosine functions in terms of the real and imaginary parts of its argument:
:
Partial fraction and product expansions of complex sine
Using the partial fraction expansion technique in complex analysis, one can find that the infinite series : both converge and are equal to . Similarly, one can show that : Using product expansion technique, one can derive : Alternatively, the infinite product for the sine can be proved using complex Fourier series. Using complex Fourier series, the function can be decomposed as : Setting yields : Therefore, we get : The function is the derivative of . Furthermore, if , then the function such that the emerged series converges on some open and connected subset of is , which can be proved using theWeierstrass M-test
In mathematics, the Weierstrass M-test is a test for determining whether an infinite series of functions converges uniformly and absolutely. It applies to series whose terms are bounded functions with real or complex values, and is analogous t ...
. The interchange of the sum and derivative is justified by uniform convergence
In the mathematical field of analysis, uniform convergence is a mode of convergence of functions stronger than pointwise convergence. A sequence of functions (f_n) converges uniformly to a limiting function f on a set E if, given any arbitrarily ...
. It follows that
:
Exponentiating gives
:
Since and , we have . Hence
:
for some open and connected subset of . Let . Since converges uniformly on any closed disk, converges uniformly on any closed disk as well. It follows that the infinite product is holomorphic on . By the identity theorem
In real analysis and complex analysis, branches of mathematics, the identity theorem for analytic functions states: given functions ''f'' and ''g'' analytic on a domain ''D'' (open and connected subset of \mathbb or \mathbb), if ''f'' = ''g'' on so ...
, the infinite product for the sine is valid for all , which completes the proof.
Usage of complex sine
sin(''z'') is found in thefunctional equation
In mathematics, a functional equation
is, in the broadest meaning, an equation in which one or several functions appear as unknowns. So, differential equations and integral equations are functional equations. However, a more restricted meaning ...
for the Gamma function
In mathematics, the gamma function (represented by , the capital letter gamma from the Greek alphabet) is one commonly used extension of the factorial function to complex numbers. The gamma function is defined for all complex numbers except ...
,
:
which in turn is found in the functional equation
In mathematics, a functional equation
is, in the broadest meaning, an equation in which one or several functions appear as unknowns. So, differential equations and integral equations are functional equations. However, a more restricted meaning ...
for the Riemann zeta-function
The Riemann zeta function or Euler–Riemann zeta function, denoted by the Greek letter (zeta), is a mathematical function of a complex variable defined as \zeta(s) = \sum_^\infty \frac = \frac + \frac + \frac + \cdots for \operatorname(s) > ...
,
:
As a holomorphic function, sin ''z'' is a 2D solution of Laplace's equation:
:
The complex sine function is also related to the level curves of pendulums
A pendulum is a weight suspended from a pivot so that it can swing freely. When a pendulum is displaced sideways from its resting, equilibrium position, it is subject to a restoring force due to gravity that will accelerate it back toward the ...
.
Complex graphs
History
 While the early study of trigonometry can be traced to antiquity, the
While the early study of trigonometry can be traced to antiquity, the trigonometric functions
In mathematics, the trigonometric functions (also called circular functions, angle functions or goniometric functions) are real functions which relate an angle of a right-angled triangle to ratios of two side lengths. They are widely used in al ...
as they are in use today were developed in the medieval period. The chord function was discovered by Hipparchus
Hipparchus (; el, Ἵππαρχος, ''Hipparkhos''; BC) was a Greek astronomer, geographer, and mathematician. He is considered the founder of trigonometry, but is most famous for his incidental discovery of the precession of the equi ...
of Nicaea
Nicaea, also known as Nicea or Nikaia (; ; grc-gre, Νίκαια, ) was an ancient Greek city in Bithynia, where located in northwestern Anatolia and is primarily known as the site of the First and Second Councils of Nicaea (the first and s ...
(180–125 BCE) and Ptolemy
Claudius Ptolemy (; grc-gre, Πτολεμαῖος, ; la, Claudius Ptolemaeus; AD) was a mathematician, astronomer, astrologer, geographer, and music theorist, who wrote about a dozen scientific treatises, three of which were of importance ...
of Roman Egypt (90–165 CE). See in particular Ptolemy's table of chords
The table of chords, created by the Greek astronomer, geometer, and geographer Ptolemy in Egypt during the 2nd century AD, is a trigonometric table in Book I, chapter 11 of Ptolemy's ''Almagest'', a treatise on mathematical astronomy. It ...
.
The sine and cosine functions can be traced to the and functions used in Indian astronomy
Astronomy has long history in Indian subcontinent stretching from pre-historic to modern times. Some of the earliest roots of Indian astronomy can be dated to the period of Indus Valley civilisation or earlier. Astronomy later developed as a dis ...
during the Gupta period
The Gupta Empire was an ancient Indian empire which existed from the early 4th century CE to late 6th century CE. At its zenith, from approximately 319 to 467 CE, it covered much of the Indian subcontinent. This period is considered as the Gold ...
('' Aryabhatiya'' and '' Surya Siddhanta''), via translation from Sanskrit to Arabic and then from Arabic to Latin.
All six trigonometric functions in current use were known in Islamic mathematics by the 9th century, as was the law of sines
In trigonometry, the law of sines, sine law, sine formula, or sine rule is an equation relating the lengths of the sides of any triangle to the sines of its angles. According to the law,
\frac \,=\, \frac \,=\, \frac \,=\, 2R,
where , and ar ...
, used in solving triangles. With the exception of the sine (which was adopted from Indian mathematics), the other five modern trigonometric functions were discovered by Arabic mathematicians, including the cosine, tangent, cotangent, secant and cosecant. Al-Khwārizmī
Muḥammad ibn Mūsā al-Khwārizmī ( ar, محمد بن موسى الخوارزمي, Muḥammad ibn Musā al-Khwārazmi; ), or al-Khwarizmi, was a Persian polymath from Khwarazm, who produced vastly influential works in mathematics, astronom ...
(c. 780–850) produced tables of sines, cosines and tangents.Jacques Sesiano, "Islamic mathematics", p. 157, in Muhammad ibn Jābir al-Harrānī al-Battānī (853–929) discovered the reciprocal functions of secant and cosecant, and produced the first table of cosecants for each degree from 1° to 90°.
The first published use of the abbreviations ''sin'', ''cos'', and ''tan'' is by the 16th-century French mathematician Albert Girard
Albert Girard () (11 October 1595 in Saint-Mihiel, France − 8 December 1632 in Leiden, The Netherlands) was a French-born mathematician. He studied at the University of Leiden. He "had early thoughts on the fundamental theorem of algebra" and g ...
; these were further promulgated by Euler (see below). The ''Opus palatinum de triangulis'' of Georg Joachim Rheticus
Georg Joachim de Porris, also known as Rheticus ( /ˈrɛtɪkəs/; 16 February 1514 – 5 December 1576), was a mathematician, astronomer, cartographer, navigational-instrument maker, medical practitioner, and teacher. He is perhaps best known for ...
, a student of Copernicus
Nicolaus Copernicus (; pl, Mikołaj Kopernik; gml, Niklas Koppernigk, german: Nikolaus Kopernikus; 19 February 1473 – 24 May 1543) was a Renaissance polymath, active as a mathematician, astronomer, and Catholic canon, who formulated ...
, was probably the first in Europe to define trigonometric functions directly in terms of right triangles instead of circles, with tables for all six trigonometric functions; this work was finished by Rheticus' student Valentin Otho in 1596.
In a paper published in 1682, Leibniz
Gottfried Wilhelm (von) Leibniz . ( – 14 November 1716) was a German polymath active as a mathematician, philosopher, scientist and diplomat. He is one of the most prominent figures in both the history of philosophy and the history of ma ...
proved that sin ''x'' is not an algebraic function In mathematics, an algebraic function is a function that can be defined
as the root of a polynomial equation. Quite often algebraic functions are algebraic expressions using a finite number of terms, involving only the algebraic operations additi ...
of ''x''. Roger Cotes
Roger Cotes (10 July 1682 – 5 June 1716) was an English mathematician, known for working closely with Isaac Newton by proofreading the second edition of his famous book, the '' Principia'', before publication. He also invented the quadratur ...
computed the derivative of sine in his ''Harmonia Mensurarum'' (1722). Leonhard Euler
Leonhard Euler ( , ; 15 April 170718 September 1783) was a Swiss mathematician, physicist, astronomer, geographer, logician and engineer who founded the studies of graph theory and topology and made pioneering and influential discoveries in ma ...
's ''Introductio in analysin infinitorum'' (1748) was mostly responsible for establishing the analytic treatment of trigonometric functions in Europe, also defining them as infinite series and presenting "Euler's formula
Euler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the fundamental relationship between the trigonometric functions and the complex exponential function. Euler's formula states that fo ...
", as well as the near-modern abbreviations ''sin.'', ''cos.'', ''tang.'', ''cot.'', ''sec.'', and ''cosec.''
Etymology
Etymologically, the word ''sine'' derives from theSanskrit
Sanskrit (; attributively , ; nominally , , ) is a classical language belonging to the Indo-Aryan branch of the Indo-European languages. It arose in South Asia after its predecessor languages had diffused there from the northwest in the late ...
word 'bow-string'
or more specifically its synonym (both adopted from Ancient Greek
Ancient Greek includes the forms of the Greek language used in ancient Greece and the ancient world from around 1500 BC to 300 BC. It is often roughly divided into the following periods: Mycenaean Greek (), Dark Ages (), the Archaic p ...
'string'See Plofker, '' Mathematics in India'', Princeton University Press, 2009, p. 257See
See Maor (1998), chapter 3, regarding the etymology.), due to visual similarity between the arc of a circle with its corresponding chord and a bow with its string (see
jyā, koti-jyā and utkrama-jyā
Jyā, koṭi-jyā and utkrama-jyā are three trigonometric functions introduced by Indian mathematicians and astronomers. The earliest known Indian treatise containing references to these functions is Surya Siddhanta. These are functions of arc ...
). This was transliterated
Transliteration is a type of conversion of a text from one script to another that involves swapping letters (thus ''trans-'' + '' liter-'') in predictable ways, such as Greek → , Cyrillic → , Greek → the digraph , Armenian → or L ...
in Arabic
Arabic (, ' ; , ' or ) is a Semitic language spoken primarily across the Arab world.Semitic languages: an international handbook / edited by Stefan Weninger; in collaboration with Geoffrey Khan, Michael P. Streck, Janet C. E.Watson; Walter ...
as , which is however meaningless in that language and abbreviated (). Since Arabic is written without short vowels, was interpreted as the homograph
A homograph (from the el, ὁμός, ''homós'', "same" and γράφω, ''gráphō'', "write") is a word that shares the same written form as another word but has a different meaning. However, some dictionaries insist that the words must also ...
, ( جيب), which means 'bosom', 'pocket', 'fold'. When the Arabic texts of Al-Battani
Abū ʿAbd Allāh Muḥammad ibn Jābir ibn Sinān al-Raqqī al-Ḥarrānī aṣ-Ṣābiʾ al-Battānī ( ar, محمد بن جابر بن سنان البتاني) ( Latinized as Albategnius, Albategni or Albatenius) (c. 858 – 929) was an astron ...
and al-Khwārizmī
Muḥammad ibn Mūsā al-Khwārizmī ( ar, محمد بن موسى الخوارزمي, Muḥammad ibn Musā al-Khwārazmi; ), or al-Khwarizmi, was a Persian polymath from Khwarazm, who produced vastly influential works in mathematics, astronom ...
were translated into Medieval Latin
Medieval Latin was the form of Literary Latin used in Roman Catholic Western Europe during the Middle Ages. In this region it served as the primary written language, though local languages were also written to varying degrees. Latin functione ...
in the 12th century by Gerard of Cremona
Gerard of Cremona (Latin: ''Gerardus Cremonensis''; c. 1114 – 1187) was an Italian translator of scientific books from Arabic into Latin. He worked in Toledo, Kingdom of Castile and obtained the Arabic books in the libraries at Toledo. Some of ...
, he used the Latin equivalent ''sinus'' (which also means 'bay' or 'fold', and more specifically 'the hanging fold of a toga
The toga (, ), a distinctive garment of ancient Rome, was a roughly semicircular cloth, between in length, draped over the shoulders and around the body. It was usually woven from white wool, and was worn over a tunic. In Roman historical tra ...
over the breast').: ''It was Robert of Chester's translation from the Arabic that resulted in our word "sine". The Hindus had given the name jiva to the half-chord in trigonometry, and the Arabs had taken this over as jiba. In the Arabic language there is also the word jaib meaning "bay" or "inlet". When Robert of Chester came to translate the technical word jiba, he seems to have confused this with the word jaib (perhaps because vowels were omitted); hence, he used the word sinus, the Latin word for "bay" or "inlet".''Victor J. Katz (2008), ''A History of Mathematics'', Boston: Addison-Wesley, 3rd. ed., p. 253, sidebar 8.1. : ''The English word “sine” comes from a series of mistranslations of the Sanskrit (chord-half). Āryabhaṭa frequently abbreviated this term to or its synonym . When some of the Hindu works were later translated into Arabic, the word was simply transcribed phonetically into an otherwise meaningless Arabic word . But since Arabic is written without vowels, later writers interpreted the consonants as , which means bosom or breast. In the twelfth century, when an Arabic trigonometry work was translated into Latin, the translator used the equivalent Latin word , which also meant bosom, and by extension, fold (as in a toga over a breast), or a bay or gulf.'' Gerard was probably not the first scholar to use this translation; Robert of Chester appears to have preceded him and there is evidence of even earlier usage. The English form ''sine'' was introduced in the 1590s.
The word ''cosine'' derives from an abbreviation of the Latin 'sine of the complementary angle
In Euclidean geometry, an angle is the figure formed by two rays, called the '' sides'' of the angle, sharing a common endpoint, called the ''vertex'' of the angle.
Angles formed by two rays lie in the plane that contains the rays. Angles ar ...
' as ''cosinus'' in Edmund Gunter
Edmund Gunter (158110 December 1626), was an English clergyman, mathematician, geometer and astronomer of Welsh descent. He is best remembered for his mathematical contributions which include the invention of the Gunter's chain, the Gunter's qu ...
's ''Canon triangulorum'' (1620), which also includes a similar definition of ''cotangens''.
Software implementations
There is no standard algorithm for calculating sine and cosine. IEEE 754, the most widely used standard for the specification of reliable floating-point computation, does not address calculating trigonometric functions such as sine. The reason is that no efficient algorithm is known for computing sine and cosine with a specified accuracy, especially for large inputs. Algorithms for calculating sine may be balanced for such constraints as speed, accuracy, portability, or range of input values accepted. This can lead to different results for different algorithms, especially for special circumstances such as very large inputs, e.g.sin(10).
A common programming optimization, used especially in 3D graphics, is to pre-calculate a table of sine values, for example one value per degree, then for values in-between pick the closest pre-calculated value, or linearly interpolate between the 2 closest values to approximate it. This allows results to be looked up from a table rather than being calculated in real time. With modern CPU architectures this method may offer no advantage.
The CORDIC
CORDIC (for "coordinate rotation digital computer"), also known as Volder's algorithm, or: Digit-by-digit method Circular CORDIC (Jack E. Volder), Linear CORDIC, Hyperbolic CORDIC (John Stephen Walther), and Generalized Hyperbolic CORDIC (GH C ...
algorithm is commonly used in scientific calculators.
The sine and cosine functions, along with other trigonometric functions, is widely available across programming languages and platforms. In computing, they are typically abbreviated to sin and cos.
Some CPU architectures have a built-in instruction for sine, including the Intel x87 FPUs since the 80387.
In programming languages, sin and cos are typically either a built-in function or found within the language's standard math library.
For example, the C standard library defines sine functions within math.h
C mathematical operations are a group of functions in the standard library of the C programming language implementing basic mathematical functions. All functions use floating-point numbers in one manner or another. Different C standards provid ...
: sin(double
A double is a look-alike or doppelgänger; one person or being that resembles another.
Double, The Double or Dubble may also refer to:
Film and television
* Double (filmmaking), someone who substitutes for the credited actor of a character
* ...
), sinf(float
Float may refer to:
Arts and entertainment Music Albums
* ''Float'' (Aesop Rock album), 2000
* ''Float'' (Flogging Molly album), 2008
* ''Float'' (Styles P album), 2013
Songs
* "Float" (Tim and the Glory Boys song), 2022
* "Float", by Bush ...
), and sinl(long double
In C and related programming languages, long double refers to a floating-point data type that is often more precise than double precision though the language standard only requires it to be at least as precise as double. As with C's other flo ...
). The parameter of each is a floating point
In computing, floating-point arithmetic (FP) is arithmetic that represents real numbers approximately, using an integer with a fixed precision, called the significand, scaled by an integer exponent of a fixed base. For example, 12.345 can b ...
value, specifying the angle in radians. Each function returns the same data type as it accepts. Many other trigonometric functions are also defined in math.h
C mathematical operations are a group of functions in the standard library of the C programming language implementing basic mathematical functions. All functions use floating-point numbers in one manner or another. Different C standards provid ...
, such as for cosine, arc sine, and hyperbolic sine (sinh).
Similarly, Python
Python may refer to:
Snakes
* Pythonidae, a family of nonvenomous snakes found in Africa, Asia, and Australia
** ''Python'' (genus), a genus of Pythonidae found in Africa and Asia
* Python (mythology), a mythical serpent
Computing
* Python (pro ...
defines math.sin(x) and math.cos(x) within the built-in math module. Complex sine and cosine functions are also available within the cmath module, e.g. cmath.sin(z). CPython
CPython is the reference implementation of the Python programming language. Written in C and Python, CPython is the default and most widely used implementation of the Python language.
CPython can be defined as both an interpreter and a compi ...
's math functions call the C math library, and use a double-precision floating-point format.
Turns based implementations
Some software libraries provide implementations of sine and cosine using the input angle in half- turns, a half-turn being an angle of 180 degrees or radians. Representing angles in turns or half-turns has accuracy advantages and efficiency advantages in some cases.MATLAB Documentation sinpi/ref>R Documentation sinpi
/ref> In MATLAB, OpenCL, R, Julia, CUDA, and ARM, these function are called
sinpi and cospi. For example, sinpi(x) would evaluate to where ''x'' is expressed in half-turns, and consequently the final input to the function, can be interpreted in radians by .
The accuracy advantage stems from the ability to perfectly represent key angles like full-turn, half-turn, and quarter-turn losslessly in binary floating-point or fixed-point. In contrast, representing , , and in binary floating-point or binary scaled fixed-point always involves a loss of accuracy since irrational numbers cannot be represented with finitely many binary digits.
Turns also have an accuracy advantage and efficiency advantage for computing modulo to one period. Computing modulo 1 turn or modulo 2 half-turns can be losslessly and efficiently computed in both floating-point and fixed-point. For example, computing modulo 1 or modulo 2 for a binary point scaled fixed-point value requires only a bit shift or bitwise AND operation. In contrast, computing modulo involves inaccuracies in representing .
For applications involving angle sensors, the sensor typically provides angle measurements in a form directly compatible with turns or half-turns. For example, an angle sensor may count from 0 to 4096 over one complete revolution./ref> If half-turns are used as the unit for angle, then the value provided by the sensor directly and losslessly maps to a fixed-point data type with 11 bits to the right of the binary point. In contrast, if radians are used as the unit for storing the angle, then the inaccuracies and cost of multiplying the raw sensor integer by an approximation to would be incurred.
See also
*Āryabhaṭa's sine table '
The astronomical treatise Āryabhaṭīya was composed during the fifth century by the Indian mathematician and astronomer Āryabhaṭa (476–550 CE), for the computation of the half-chords of certain set of arcs of a circle. It is not a tabl ...
* Bhaskara I's sine approximation formula
In mathematics, Bhaskara I's sine approximation formula is a rational expression in one variable for the computation of the approximate values of the trigonometric sines discovered by Bhaskara I (c. 600 – c. 680), a seventh-century Indian ma ...
* Discrete sine transform
* Euler's formula
Euler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the fundamental relationship between the trigonometric functions and the complex exponential function. Euler's formula states that fo ...
* Generalized trigonometry
* Hyperbolic function
In mathematics, hyperbolic functions are analogues of the ordinary trigonometric functions, but defined using the hyperbola rather than the circle. Just as the points form a circle with a unit radius, the points form the right half of the u ...
* Dixon elliptic functions
In mathematics, the Dixon elliptic functions sm and cm are two elliptic functions ( doubly periodic meromorphic functions on the complex plane) that map from each regular hexagon in a hexagonal tiling to the whole complex plane. Because these f ...
* Lemniscate elliptic functions
In mathematics, the lemniscate elliptic functions are elliptic functions related to the arc length of the lemniscate of Bernoulli. They were first studied by Giulio Fagnano in 1718 and later by Leonhard Euler and Carl Friedrich Gauss, among othe ...
* Law of sines
In trigonometry, the law of sines, sine law, sine formula, or sine rule is an equation relating the lengths of the sides of any triangle to the sines of its angles. According to the law,
\frac \,=\, \frac \,=\, \frac \,=\, 2R,
where , and ar ...
* List of periodic functions
This is a list of some well-known periodic functions. The constant function , where is independent of , is periodic with any period, but lacks a ''fundamental period''. A definition is given for some of the following functions, though each funct ...
* List of trigonometric identities
In trigonometry, trigonometric identities are equalities that involve trigonometric functions and are true for every value of the occurring variables for which both sides of the equality are defined. Geometrically, these are identities involvin ...
* Madhava series
In mathematics, a Madhava series or Leibniz series is any one of the series in a collection of infinite series expressions all of which are believed to have been discovered by an Indian Mathematician and Astronomer Madhava of Sangamagrama (c.&nb ...
* Madhava's sine table
Madhava's sine table is the table of trigonometric sines of various angles constructed by the 14th century Kerala mathematician-astronomer Madhava of Sangamagrama. The table lists the trigonometric sines of the twenty-four angles 3.75°, 7.5 ...
* Optical sine theorem In optics
Optics is the branch of physics that studies the behaviour and properties of light, including its interactions with matter and the construction of instruments that use or detect it. Optics usually describes the behaviour of visibl ...
* Polar sine In geometry, the polar sine generalizes the sine function of angle to the vertex angle of a polytope. It is denoted by psin.
Definition
''n'' vectors in ''n''-dimensional space
Let v1, ..., v''n'' (''n'' ≥ 2) be non-zer ...
—a generalization to vertex angles
* Proofs of trigonometric identities
There are several equivalent ways for defining trigonometric functions, and the proof of the trigonometric identities between them depend on the chosen definition. The oldest and somehow the most elementary definition is based on the geometry of r ...
* Sinc function
* Sine and cosine transforms In mathematics, the Fourier sine and cosine transforms are forms of the Fourier transform that do not use complex numbers or require negative frequency. They are the forms originally used by Joseph Fourier and are still preferred in some application ...
* Sine integral
In mathematics, trigonometric integrals are a family of integrals involving trigonometric functions.
Sine integral
The different sine integral definitions are
\operatorname(x) = \int_0^x\frac\,dt
\operatorname(x) = -\int_x^\infty\frac ...
* Sine quadrant
* Sine wave
* Sine–Gordon equation
* Sinusoidal model
In statistics, signal processing, and time series analysis, a sinusoidal model is used to approximate a sequence ''Yi'' to a sine function:
:Y_i = C + \alpha\sin(\omega T_i + \phi) + E_i
where ''C'' is constant defining a mean level, α is an ...
* SOH-CAH-TOA
* Trigonometric functions
In mathematics, the trigonometric functions (also called circular functions, angle functions or goniometric functions) are real functions which relate an angle of a right-angled triangle to ratios of two side lengths. They are widely used in al ...
* Trigonometric integral
In mathematics, trigonometric integrals are a family of integrals involving trigonometric functions.
Sine integral
The different sine integral definitions are
\operatorname(x) = \int_0^x\frac\,dt
\operatorname(x) = -\int_x^\infty\fra ...
Citations
References
* *External links
* {{Trigonometric and hyperbolic functions Angle Trigonometric functions no:Trigonometriske funksjoner#Sinus, cosinus og tangens