Shell theorem on:
[Wikipedia]
[Google]
[Amazon]
In
 Suppose that this mass is moved upwards along the ''y''-axis to the point The distance between and the point mass is now longer than before; It becomes the hypotenuse of the right triangle with legs and which is Hence, the gravitational field of the elevated point is:
Suppose that this mass is moved upwards along the ''y''-axis to the point The distance between and the point mass is now longer than before; It becomes the hypotenuse of the right triangle with legs and which is Hence, the gravitational field of the elevated point is:
 The magnitude of the gravitational field that would pull a particle at point in the ''x''-direction is the gravitational field multiplied by where is the angle adjacent to the ''x''-axis. In this case, Hence, the magnitude of the gravitational field in the ''x''-direction, is:
Substituting in gives
Suppose that this mass is evenly distributed in a ring centered at the origin and facing point with the same radius Because all of the mass is located at the same angle with respect to the ''x''-axis, and the distance between the points on the ring is the same distance as before, the gravitational field in the ''x''-direction at point due to the ring is the same as a point mass located at a point units above the ''y''-axis:
The magnitude of the gravitational field that would pull a particle at point in the ''x''-direction is the gravitational field multiplied by where is the angle adjacent to the ''x''-axis. In this case, Hence, the magnitude of the gravitational field in the ''x''-direction, is:
Substituting in gives
Suppose that this mass is evenly distributed in a ring centered at the origin and facing point with the same radius Because all of the mass is located at the same angle with respect to the ''x''-axis, and the distance between the points on the ring is the same distance as before, the gravitational field in the ''x''-direction at point due to the ring is the same as a point mass located at a point units above the ''y''-axis:
 To find the gravitational field at point due to a disc, an infinite number of infinitely thin rings facing each with a radius width of and mass of may be placed inside one another to form a disc. The mass of any one of the rings is the mass of the disc multiplied by the ratio of the area of the ring to the total area of the disc So, Hence, a small change in the gravitational field, is:
To find the gravitational field at point due to a disc, an infinite number of infinitely thin rings facing each with a radius width of and mass of may be placed inside one another to form a disc. The mass of any one of the rings is the mass of the disc multiplied by the ratio of the area of the ring to the total area of the disc So, Hence, a small change in the gravitational field, is:
 Substituting in and integrating both sides gives the gravitational field of the disk:
Adding up the contribution to the gravitational field from each of these rings will yield the expression for the gravitational field due to a disc. This is equivalent to integrating this above expression from to resulting in:
To find the gravitational field at point due to a sphere centered at the origin, an infinite amount of infinitely thin discs facing each with a radius width of and mass of may be placed together.
These discs' radii follow the height of the cross section of a sphere (with constant radius ) which is an equation of a semi-circle: varies from to
The mass of any of the discs is the mass of the sphere multiplied by the ratio of the volume of an infinitely thin disc divided by the volume of a sphere (with constant radius The volume of an infinitely thin disc is or So, Simplifying gives
Each discs' position away from will vary with its position within the 'sphere' made of the discs, so must be replaced with
Substituting in and integrating both sides gives the gravitational field of the disk:
Adding up the contribution to the gravitational field from each of these rings will yield the expression for the gravitational field due to a disc. This is equivalent to integrating this above expression from to resulting in:
To find the gravitational field at point due to a sphere centered at the origin, an infinite amount of infinitely thin discs facing each with a radius width of and mass of may be placed together.
These discs' radii follow the height of the cross section of a sphere (with constant radius ) which is an equation of a semi-circle: varies from to
The mass of any of the discs is the mass of the sphere multiplied by the ratio of the volume of an infinitely thin disc divided by the volume of a sphere (with constant radius The volume of an infinitely thin disc is or So, Simplifying gives
Each discs' position away from will vary with its position within the 'sphere' made of the discs, so must be replaced with
 Replacing with with and with in the 'disc' equation yields:
Simplifying,
Integrating the gravitational field of each thin disc from to with respect to and doing some careful algebra, yields Newton's shell theorem:
where is the distance between the center of the spherical mass and an arbitrary point The gravitational field of a spherical mass may be calculated by treating all the mass as a point particle at the center of the sphere.
Replacing with with and with in the 'disc' equation yields:
Simplifying,
Integrating the gravitational field of each thin disc from to with respect to and doing some careful algebra, yields Newton's shell theorem:
where is the distance between the center of the spherical mass and an arbitrary point The gravitational field of a spherical mass may be calculated by treating all the mass as a point particle at the center of the sphere.
 (Note: the in the diagram refers to the small angle, not the
(Note: the in the diagram refers to the small angle, not the 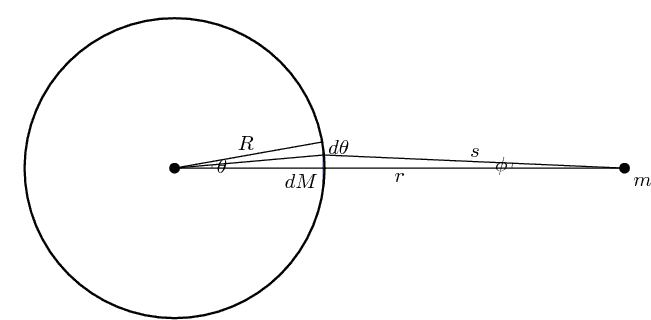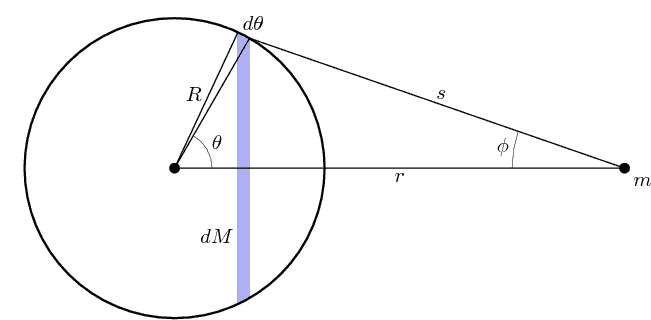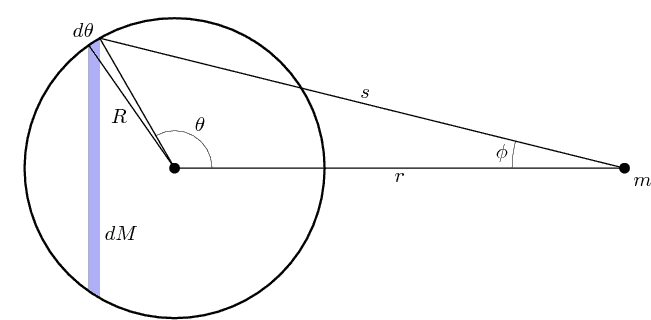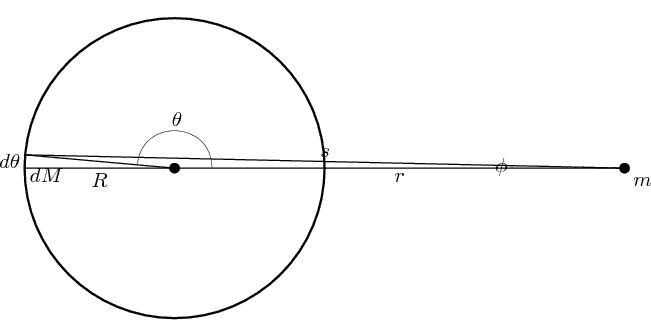 (Note: As viewed from the shaded blue band appears as a thin annulus whose inner and outer radii converge to as vanishes.)
To find a
(Note: As viewed from the shaded blue band appears as a thin annulus whose inner and outer radii converge to as vanishes.)
To find a
 Inserting these bounds into the
Inserting these bounds into the
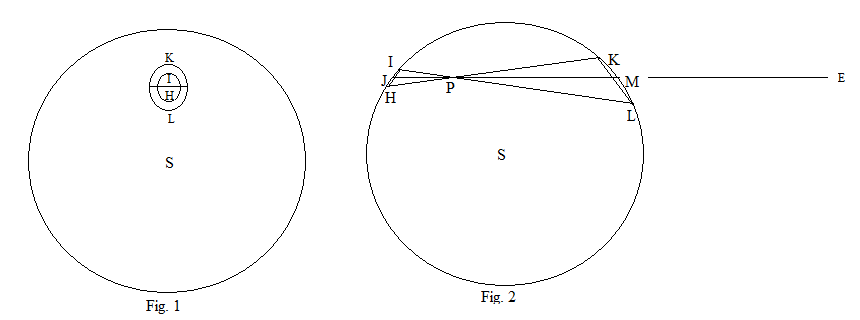 Fig. 2 is a cross-section of the hollow sphere through the center, S and an arbitrary point, P, inside the sphere. Through P draw two lines IL and HK such that the angle KPL is very small. JM is the line through P that bisects that angle. From the geometry of circles, the triangles IPH and KPL are similar. The lines KH and IL are rotated about the axis JM to form 2 cones that intersect the sphere in 2 closed curves. In Fig. 1 the sphere is seen from a distance along the line PE and is assumed transparent so both curves can be seen.
The surface of the sphere that the cones intersect can be considered to be flat, and
Since the intersection of a cone with a plane is an ellipse, in this case the intersections form two ellipses with major axes IH and KL, where
By a similar argument, the minor axes are in the same ratio. This is clear if the sphere is viewed from above. Therefore the two ellipses are similar, so their areas are as the squares of their major axes. As the mass of any section of the surface is proportional to the area of that section, for the 2 elliptical areas the ratios of their masses
Since the force of attraction on P in the direction JM from either of the elliptic areas, is direct as the mass of the area and inversely as the square of its distance from P, it is independent of the distance of P from the sphere. Hence, the forces on P from the 2 infinitesimal elliptical areas are equal and opposite and there is no net force in the direction JM.
As the position of P and the direction of JM are both arbitrary, it follows that any particle inside a hollow sphere experiences no net force from the mass of the sphere.
Note: Newton simply describes the arcs IH and KL as 'minimally small' and the areas traced out by the lines IL and HK can be any shape, not necessarily elliptic, but they will always be similar.
Fig. 2 is a cross-section of the hollow sphere through the center, S and an arbitrary point, P, inside the sphere. Through P draw two lines IL and HK such that the angle KPL is very small. JM is the line through P that bisects that angle. From the geometry of circles, the triangles IPH and KPL are similar. The lines KH and IL are rotated about the axis JM to form 2 cones that intersect the sphere in 2 closed curves. In Fig. 1 the sphere is seen from a distance along the line PE and is assumed transparent so both curves can be seen.
The surface of the sphere that the cones intersect can be considered to be flat, and
Since the intersection of a cone with a plane is an ellipse, in this case the intersections form two ellipses with major axes IH and KL, where
By a similar argument, the minor axes are in the same ratio. This is clear if the sphere is viewed from above. Therefore the two ellipses are similar, so their areas are as the squares of their major axes. As the mass of any section of the surface is proportional to the area of that section, for the 2 elliptical areas the ratios of their masses
Since the force of attraction on P in the direction JM from either of the elliptic areas, is direct as the mass of the area and inversely as the square of its distance from P, it is independent of the distance of P from the sphere. Hence, the forces on P from the 2 infinitesimal elliptical areas are equal and opposite and there is no net force in the direction JM.
As the position of P and the direction of JM are both arbitrary, it follows that any particle inside a hollow sphere experiences no net force from the mass of the sphere.
Note: Newton simply describes the arcs IH and KL as 'minimally small' and the areas traced out by the lines IL and HK can be any shape, not necessarily elliptic, but they will always be similar.
 Fig. 1 is a cross-section of the hollow sphere through the center, S with an arbitrary point, P, outside the sphere. PT is the tangent to the circle at T which passes through P. HI is a small arc on the surface such that PH is less than PT. Extend PI to intersect the sphere at L and draw SF to the point F that bisects IL. Extend PH to intersect the sphere at K and draw SE to the point E that bisects HK, and extend SF to intersect HK at D. Drop a perpendicular IQ on to the line PS joining P to the center S. Let the radius of the sphere be a and the distance PS be D.
Let arc IH be extended perpendicularly out of the plane of the diagram, by a small distance ζ. The area of the figure generated is and its mass is proportional to this product.
The force due to this mass on the particle at P and is along the line PI.
The component of this force towards the center .
If now the arc ''HI'' is rotated completely about the line ''PS'' to form a ring of width ''HI'' and radius ''IQ'', the length of the ring is 2·''IQ'' and its area is 2·''IQ''·''IH''. The component of the force due to this ring on the particle at ''P'' in the direction PS becomes
The perpendicular components of the force directed towards ''PS'' cancel out since the mass in the ring is distributed symmetrically about ''PS''. Therefore, the component in the direction ''PS'' is the total force on ''P'' due to the ring formed by rotating arc ''HI'' about ''PS''.
From similar triangles: and
If HI is sufficiently small that it can be taken as a straight line, is a right angle, and so that
Hence the force on ''P'' due to the ring
Assume now in Fig. 2 that another particle is outside the sphere at a point ''p'', a different distance ''d'' from the center of the sphere, with corresponding points lettered in lower case. For easy comparison, the construction of ''P'' in Fig. 1 is also shown in Fig. 2. As before, ''ph'' is less than ''pt''.
Generate a ring with width ih and radius iq by making angle and the slightly larger angle so that the distance PS is subtended by the same angle at I as is pS at i. The same holds for H and h, respectively.
The total force on p due to this ring is
:
Clearly and
Newton claims that DF and df can be taken as equal in the limit as the angles DPF and dpf 'vanish together'. Note that angles DPF and dpf are not equal. Although DS and dS become equal in the limit, this does not imply that the ratio of DF to df becomes equal to unity, when DF and df both approach zero. In the finite case DF depends on D, and df on d, so they are not equal.
Since the ratio of DF to df in the limit is crucial, more detailed analysis is required. From the similar right triangles, and giving Solving the quadratic for DF, in the limit as ES approaches FS, the smaller root, More simply, as DF approaches zero, in the limit the term can be ignored: leading to the same result. Clearly df has the same limit, justifying Newton’s claim.
Comparing the force from the ring HI rotated about PS to the ring hi about pS, the ratio of these 2 forces equals
By dividing up the arcs AT and Bt into corresponding infinitesimal rings, it follows that the ratio of the force due to the arc AT rotated about PS to that of Bt rotated about pS is in the same ratio, and similarly, the ratio of the forces due to arc TB to that of tA both rotated are in the same ratio.
Therefore, the force on a particle any distance D from the center of the hollow sphere is inversely proportional to which proves the proposition.
Fig. 1 is a cross-section of the hollow sphere through the center, S with an arbitrary point, P, outside the sphere. PT is the tangent to the circle at T which passes through P. HI is a small arc on the surface such that PH is less than PT. Extend PI to intersect the sphere at L and draw SF to the point F that bisects IL. Extend PH to intersect the sphere at K and draw SE to the point E that bisects HK, and extend SF to intersect HK at D. Drop a perpendicular IQ on to the line PS joining P to the center S. Let the radius of the sphere be a and the distance PS be D.
Let arc IH be extended perpendicularly out of the plane of the diagram, by a small distance ζ. The area of the figure generated is and its mass is proportional to this product.
The force due to this mass on the particle at P and is along the line PI.
The component of this force towards the center .
If now the arc ''HI'' is rotated completely about the line ''PS'' to form a ring of width ''HI'' and radius ''IQ'', the length of the ring is 2·''IQ'' and its area is 2·''IQ''·''IH''. The component of the force due to this ring on the particle at ''P'' in the direction PS becomes
The perpendicular components of the force directed towards ''PS'' cancel out since the mass in the ring is distributed symmetrically about ''PS''. Therefore, the component in the direction ''PS'' is the total force on ''P'' due to the ring formed by rotating arc ''HI'' about ''PS''.
From similar triangles: and
If HI is sufficiently small that it can be taken as a straight line, is a right angle, and so that
Hence the force on ''P'' due to the ring
Assume now in Fig. 2 that another particle is outside the sphere at a point ''p'', a different distance ''d'' from the center of the sphere, with corresponding points lettered in lower case. For easy comparison, the construction of ''P'' in Fig. 1 is also shown in Fig. 2. As before, ''ph'' is less than ''pt''.
Generate a ring with width ih and radius iq by making angle and the slightly larger angle so that the distance PS is subtended by the same angle at I as is pS at i. The same holds for H and h, respectively.
The total force on p due to this ring is
:
Clearly and
Newton claims that DF and df can be taken as equal in the limit as the angles DPF and dpf 'vanish together'. Note that angles DPF and dpf are not equal. Although DS and dS become equal in the limit, this does not imply that the ratio of DF to df becomes equal to unity, when DF and df both approach zero. In the finite case DF depends on D, and df on d, so they are not equal.
Since the ratio of DF to df in the limit is crucial, more detailed analysis is required. From the similar right triangles, and giving Solving the quadratic for DF, in the limit as ES approaches FS, the smaller root, More simply, as DF approaches zero, in the limit the term can be ignored: leading to the same result. Clearly df has the same limit, justifying Newton’s claim.
Comparing the force from the ring HI rotated about PS to the ring hi about pS, the ratio of these 2 forces equals
By dividing up the arcs AT and Bt into corresponding infinitesimal rings, it follows that the ratio of the force due to the arc AT rotated about PS to that of Bt rotated about pS is in the same ratio, and similarly, the ratio of the forces due to arc TB to that of tA both rotated are in the same ratio.
Therefore, the force on a particle any distance D from the center of the hollow sphere is inversely proportional to which proves the proposition.
classical mechanics
Classical mechanics is a physical theory describing the motion of macroscopic objects, from projectiles to parts of machinery, and astronomical objects, such as spacecraft, planets, stars, and galaxies. For objects governed by classi ...
, the shell theorem gives gravitational
In physics, gravity () is a fundamental interaction which causes mutual attraction between all things with mass or energy. Gravity is, by far, the weakest of the four fundamental interactions, approximately 1038 times weaker than the stron ...
simplifications that can be applied to objects inside or outside a spherically symmetrical
Symmetry (from grc, συμμετρία "agreement in dimensions, due proportion, arrangement") in everyday language refers to a sense of harmonious and beautiful proportion and balance. In mathematics, "symmetry" has a more precise definiti ...
body. This theorem has particular application to astronomy
Astronomy () is a natural science that studies celestial objects and phenomena. It uses mathematics, physics, and chemistry in order to explain their origin and evolution. Objects of interest include planets, moons, stars, nebulae, g ...
.
Isaac Newton
Sir Isaac Newton (25 December 1642 – 20 March 1726/27) was an English mathematician, physicist, astronomer, alchemist, theologian, and author (described in his time as a " natural philosopher"), widely recognised as one of the grea ...
proved the shell theorem and stated that:
# A spherically symmetric
Symmetry (from grc, συμμετρία "agreement in dimensions, due proportion, arrangement") in everyday language refers to a sense of harmonious and beautiful proportion and balance. In mathematics, "symmetry" has a more precise definiti ...
body affects external objects gravitationally as though all of its mass
Mass is an intrinsic property of a body. It was traditionally believed to be related to the quantity of matter in a physical body, until the discovery of the atom and particle physics. It was found that different atoms and different eleme ...
were concentrated at a point
Point or points may refer to:
Places
* Point, Lewis, a peninsula in the Outer Hebrides, Scotland
* Point, Texas, a city in Rains County, Texas, United States
* Point, the NE tip and a ferry terminal of Lismore, Inner Hebrides, Scotland
* Point ...
at its center.
# If the body is a spherically symmetric shell (i.e., a hollow ball), no net gravitational force
In physics, gravity () is a fundamental interaction which causes mutual attraction between all things with mass or energy. Gravity is, by far, the weakest of the four fundamental interactions, approximately 1038 times weaker than the strong ...
is exerted by the shell on any object inside, regardless of the object's location within the shell.
A corollary is that inside a solid sphere of constant density, the gravitational force within the object varies linearly with distance from the center, becoming zero by symmetry at the center of mass
Mass is an intrinsic property of a body. It was traditionally believed to be related to the quantity of matter in a physical body, until the discovery of the atom and particle physics. It was found that different atoms and different eleme ...
. This can be seen as follows: take a point within such a sphere, at a distance from the center of the sphere. Then you can ignore all of the shells of greater radius, according to the shell theorem (1). But the point can be considered to be external to the remaining sphere of radius r, and according to (2) all of the mass of this sphere can be considered to be concentrated at its centre. The remaining mass is proportional to (because it is based on volume). The gravitational force exerted on a body at radius r will be proportional to (the inverse square law), so the overall gravitational effect is proportional to so is linear in
These results were important to Newton's analysis of planetary motion; they are not immediately obvious, but they can be proven with calculus
Calculus, originally called infinitesimal calculus or "the calculus of infinitesimals", is the mathematical study of continuous change, in the same way that geometry is the study of shape, and algebra is the study of generalizations of arithm ...
. (Gauss's law for gravity
In physics, Gauss's law for gravity, also known as Gauss's flux theorem for gravity, is a law of physics that is equivalent to Newton's law of universal gravitation. It is named after Carl Friedrich Gauss. It states that the flux ( surface inte ...
offers an alternative way to state the theorem.)
In addition to gravity
In physics, gravity () is a fundamental interaction which causes mutual attraction between all things with mass or energy. Gravity is, by far, the weakest of the four fundamental interactions, approximately 1038 times weaker than the stro ...
, the shell theorem can also be used to describe the electric field generated by a static spherically symmetric charge density
In electromagnetism, charge density is the amount of electric charge per unit length, surface area, or volume. Volume charge density (symbolized by the Greek letter ρ) is the quantity of charge per unit volume, measured in the SI system in ...
, or similarly for any other phenomenon that follows an inverse square law. The derivations below focus on gravity, but the results can easily be generalized to the electrostatic force
Coulomb's inverse-square law, or simply Coulomb's law, is an experimental law of physics that quantifies the amount of force between two stationary, electrically charged particles. The electric force between charged bodies at rest is convention ...
.
Derivation of gravitational field outside of a solid sphere
There are three steps to proving Newton's shell theorem. First, the equation for a gravitational field due to a ring of mass will be derived. Arranging an infinite number of infinitely thin rings to make a disc, this equation involving a ring will be used to find the gravitational field due to a disk. Finally, arranging an infinite number of infinitely thin discs to make a sphere, this equation involving a disc will be used to find the gravitational field due to a sphere. The gravitational field at a position called at on the ''x''-axis due to a point of mass at the origin is Suppose that this mass is moved upwards along the ''y''-axis to the point The distance between and the point mass is now longer than before; It becomes the hypotenuse of the right triangle with legs and which is Hence, the gravitational field of the elevated point is:
Suppose that this mass is moved upwards along the ''y''-axis to the point The distance between and the point mass is now longer than before; It becomes the hypotenuse of the right triangle with legs and which is Hence, the gravitational field of the elevated point is:
 The magnitude of the gravitational field that would pull a particle at point in the ''x''-direction is the gravitational field multiplied by where is the angle adjacent to the ''x''-axis. In this case, Hence, the magnitude of the gravitational field in the ''x''-direction, is:
Substituting in gives
Suppose that this mass is evenly distributed in a ring centered at the origin and facing point with the same radius Because all of the mass is located at the same angle with respect to the ''x''-axis, and the distance between the points on the ring is the same distance as before, the gravitational field in the ''x''-direction at point due to the ring is the same as a point mass located at a point units above the ''y''-axis:
The magnitude of the gravitational field that would pull a particle at point in the ''x''-direction is the gravitational field multiplied by where is the angle adjacent to the ''x''-axis. In this case, Hence, the magnitude of the gravitational field in the ''x''-direction, is:
Substituting in gives
Suppose that this mass is evenly distributed in a ring centered at the origin and facing point with the same radius Because all of the mass is located at the same angle with respect to the ''x''-axis, and the distance between the points on the ring is the same distance as before, the gravitational field in the ''x''-direction at point due to the ring is the same as a point mass located at a point units above the ''y''-axis:
 To find the gravitational field at point due to a disc, an infinite number of infinitely thin rings facing each with a radius width of and mass of may be placed inside one another to form a disc. The mass of any one of the rings is the mass of the disc multiplied by the ratio of the area of the ring to the total area of the disc So, Hence, a small change in the gravitational field, is:
To find the gravitational field at point due to a disc, an infinite number of infinitely thin rings facing each with a radius width of and mass of may be placed inside one another to form a disc. The mass of any one of the rings is the mass of the disc multiplied by the ratio of the area of the ring to the total area of the disc So, Hence, a small change in the gravitational field, is:
 Substituting in and integrating both sides gives the gravitational field of the disk:
Adding up the contribution to the gravitational field from each of these rings will yield the expression for the gravitational field due to a disc. This is equivalent to integrating this above expression from to resulting in:
To find the gravitational field at point due to a sphere centered at the origin, an infinite amount of infinitely thin discs facing each with a radius width of and mass of may be placed together.
These discs' radii follow the height of the cross section of a sphere (with constant radius ) which is an equation of a semi-circle: varies from to
The mass of any of the discs is the mass of the sphere multiplied by the ratio of the volume of an infinitely thin disc divided by the volume of a sphere (with constant radius The volume of an infinitely thin disc is or So, Simplifying gives
Each discs' position away from will vary with its position within the 'sphere' made of the discs, so must be replaced with
Substituting in and integrating both sides gives the gravitational field of the disk:
Adding up the contribution to the gravitational field from each of these rings will yield the expression for the gravitational field due to a disc. This is equivalent to integrating this above expression from to resulting in:
To find the gravitational field at point due to a sphere centered at the origin, an infinite amount of infinitely thin discs facing each with a radius width of and mass of may be placed together.
These discs' radii follow the height of the cross section of a sphere (with constant radius ) which is an equation of a semi-circle: varies from to
The mass of any of the discs is the mass of the sphere multiplied by the ratio of the volume of an infinitely thin disc divided by the volume of a sphere (with constant radius The volume of an infinitely thin disc is or So, Simplifying gives
Each discs' position away from will vary with its position within the 'sphere' made of the discs, so must be replaced with
 Replacing with with and with in the 'disc' equation yields:
Simplifying,
Integrating the gravitational field of each thin disc from to with respect to and doing some careful algebra, yields Newton's shell theorem:
where is the distance between the center of the spherical mass and an arbitrary point The gravitational field of a spherical mass may be calculated by treating all the mass as a point particle at the center of the sphere.
Replacing with with and with in the 'disc' equation yields:
Simplifying,
Integrating the gravitational field of each thin disc from to with respect to and doing some careful algebra, yields Newton's shell theorem:
where is the distance between the center of the spherical mass and an arbitrary point The gravitational field of a spherical mass may be calculated by treating all the mass as a point particle at the center of the sphere.
Outside a shell
A solid, sphericallysymmetric
Symmetry (from grc, συμμετρία "agreement in dimensions, due proportion, arrangement") in everyday language refers to a sense of harmonious and beautiful proportion and balance. In mathematics, "symmetry" has a more precise definiti ...
body can be modeled as an infinite number of concentric, infinitesimally thin spherical shells. If one of these shells can be treated as a point mass, then a system of shells (i.e. the sphere) can also be treated as a point mass. Consider one such shell (the diagram shows a cross-section):
arc length
ARC may refer to:
Business
* Aircraft Radio Corporation, a major avionics manufacturer from the 1920s to the '50s
* Airlines Reporting Corporation, an airline-owned company that provides ticket distribution, reporting, and settlement services
* ...
. The arc length is
Applying Newton's Universal Law of Gravitation, the sum of the forces due to the mass elements in the shaded band is
:
However, since there is partial cancellation due to the vector
Vector most often refers to:
*Euclidean vector, a quantity with a magnitude and a direction
*Vector (epidemiology), an agent that carries and transmits an infectious pathogen into another living organism
Vector may also refer to:
Mathematic ...
nature of the force in conjunction with the circular band's symmetry, the leftover component
Circuit Component may refer to:
•Are devices that perform functions when they are connected in a circuit.
In engineering, science, and technology Generic systems
* System components, an entity with discrete structure, such as an assem ...
(in the direction pointing towards is given by
:
The total force on then, is simply the sum of the force exerted by all the bands. By shrinking the width of each band, and increasing the number of bands, the sum becomes an integral expression:
:
Since and are constants, they may be taken out of the integral:
:
To evaluate this integral, one must first express as a function of
The total surface of a spherical shell is
:
while the surface area of the thin slice between and is
:
If the mass of the shell is one therefore has that
:
and
:
By the law of cosines
In trigonometry, the law of cosines (also known as the cosine formula, cosine rule, or al-Kashi's theorem) relates the lengths of the sides of a triangle to the cosine of one of its angles. Using notation as in Fig. 1, the law of cosines states ...
,
:
and
:
These two relations link the three parameters and that appear in the integral together. As increases from to radians, varies from the initial value 0 to a maximal value before finally returning to zero At the same time, increases from the initial value to the final value as increases from 0 to radians. This is illustrated in the following animation:
 (Note: As viewed from the shaded blue band appears as a thin annulus whose inner and outer radii converge to as vanishes.)
To find a
(Note: As viewed from the shaded blue band appears as a thin annulus whose inner and outer radii converge to as vanishes.)
To find a primitive function
In calculus, an antiderivative, inverse derivative, primitive function, primitive integral or indefinite integral of a function is a differentiable function whose derivative is equal to the original function . This can be stated symbolicall ...
to the integrand, one has to make the independent integration variable instead of
Performing an implicit differentiation
In mathematics, an implicit equation is a relation of the form R(x_1, \dots, x_n) = 0, where is a function of several variables (often a polynomial). For example, the implicit equation of the unit circle is x^2 + y^2 - 1 = 0.
An implicit func ...
of the second of the "cosine law" expressions above yields
:
and thus
:
It follows that
:
where the new integration variable increases from
Inserting the expression for using the first of the "cosine law" expressions above, one finally gets that
:
A primitive function
In calculus, an antiderivative, inverse derivative, primitive function, primitive integral or indefinite integral of a function is a differentiable function whose derivative is equal to the original function . This can be stated symbolicall ...
to the integrand is
:
and inserting the bounds and for the integration variable in this primitive function, one gets that
:
saying that the gravitational force is the same as that of a point mass in the center of the shell with the same mass.
Finally, integrate all infinitesimally thin spherical shell with mass of and we can obtain the total gravity contribution of a solid ball to the object outside the ball
:
Between the radius of to can be expressed as a function of i.e.,
:
Therefore, the total gravity is
:
which suggests that the gravity of a solid spherical ball to an exterior object can be simplified as that of a point mass in the center of the ball with the same mass.
Inside a shell
For a point inside the shell, the difference is that when ''θ'' is equal to zero, ''ϕ'' takes the value radians and ''s'' the value . When ''θ'' increases from 0 to radians, ''ϕ'' decreases from the initial value radians to zero and ''s'' increases from the initial value to the value . This can all be seen in the following figureprimitive function
In calculus, an antiderivative, inverse derivative, primitive function, primitive integral or indefinite integral of a function is a differentiable function whose derivative is equal to the original function . This can be stated symbolicall ...
:
one gets that, in this case
:
saying that the net gravitational forces acting on the point mass from the mass elements of the shell, outside the measurement point, cancel out.
Generalization: If the resultant force inside the shell is:
:
The above results into being identically zero if and only if
Outside the shell (i.e. or ):
:
Derivation using Gauss's law
The shell theorem is an immediate consequence ofGauss's law for gravity
In physics, Gauss's law for gravity, also known as Gauss's flux theorem for gravity, is a law of physics that is equivalent to Newton's law of universal gravitation. It is named after Carl Friedrich Gauss. It states that the flux ( surface inte ...
saying that
:
where ''M'' is the mass of the part of the spherically symmetric mass distribution that is inside the sphere with radius ''r'' and
:
is the surface integral of the gravitational field g over any closed surface
In the part of mathematics referred to as topology, a surface is a two-dimensional manifold. Some surfaces arise as the boundaries of three-dimensional solids; for example, the sphere is the boundary of the solid ball. Other surfaces arise as g ...
inside which the total mass is ''M'', the unit vector
In mathematics, a unit vector in a normed vector space is a vector (often a spatial vector) of length 1. A unit vector is often denoted by a lowercase letter with a circumflex, or "hat", as in \hat (pronounced "v-hat").
The term ''direction v ...
being the outward normal to the surface.
The gravitational field of a spherically symmetric mass distribution like a mass point, a spherical shell or a homogeneous sphere must also be spherically symmetric. If is a unit vector in the direction from the point of symmetry to another point the gravitational field at this other point must therefore be
:
where ''g''(''r'') only depends on the distance ''r'' to the point of symmetry
Selecting the closed surface as a sphere with radius ''r'' with center at the point of symmetry the outward normal to a point on the surface, is precisely the direction pointing away from the point of symmetry of the mass distribution.
One, therefore, has that
:
and
:
as the area of the sphere is 4''r''2.
From Gauss's law it then follows that
:
or,
:
Converses and generalizations
It is natural to ask whether theconverse
Converse may refer to:
Mathematics and logic
* Converse (logic), the result of reversing the two parts of a definite or implicational statement
** Converse implication, the converse of a material implication
** Converse nonimplication, a logical c ...
of the shell theorem is true, namely whether the result of the theorem implies the law of universal gravitation, or if there is some more general force law for which the theorem holds. More specifically, one may ask the question:
In fact, this allows exactly one more class of force than the (Newtonian) inverse square. http://adsabs.harvard.edu/full/1985Obs...105...42G The most general force as derived by Vahe Gurzadyan
Vahagn "Vahe" Gurzadyan ( hy, Վահագն Գուրզադյան; born 21 November 1955) is an Armenian mathematical physicist and a professor and head of Cosmology Center at Yerevan Physics Institute, Yerevan , Armenia, best known for co-writi ...
in Gurzadyan theorem In cosmology, Gurzadyan theorem, proved by Vahe Gurzadyan, states the most general functional form for the force satisfying the condition of identity of the gravity of the sphere and of a point mass located in the sphere's center. This theorem thus ...
is:"
:
where and can be constants taking any value. The first term is the familiar law of universal gravitation; the second is an additional force, analogous to the cosmological constant
In cosmology, the cosmological constant (usually denoted by the Greek capital letter lambda: ), alternatively called Einstein's cosmological constant,
is the constant coefficient of a term that Albert Einstein temporarily added to his field eq ...
term in general relativity
General relativity, also known as the general theory of relativity and Einstein's theory of gravity, is the geometric theory of gravitation published by Albert Einstein in 1915 and is the current description of gravitation in modern physics ...
.
If we further constrain the force by requiring that the second part of the theorem also holds, namely that there is no force inside a hollow ball, we exclude the possibility of the additional term, and the inverse square law is indeed the unique force law satisfying the theorem.
On the other hand, if we relax the conditions, and require only that the field everywhere outside a spherically symmetric body is the same as the field from some point mass at the center (of any mass), we allow a new class of solutions given by the Yukawa potential
In particle, atomic and condensed matter physics, a Yukawa potential (also called a screened Coulomb potential) is a potential named after the Japanese physicist Hideki Yukawa. The potential is of the form:
:V_\text(r)= -g^2\frac,
where is a ...
, of which the inverse square law is a special case.
Another generalization can be made for a disc by observing that
:
so:
:
where and is the density of the body.
Doing all the intermediate calculations we get:
:
Newton's proofs
Introduction
Propositions 70 and 71 consider the force acting on a particle from a hollow sphere with an infinitesimally thin surface, whose mass density is constant over the surface. The force on the particle from a small area of the surface of the sphere is proportional to the mass of the area and inversely as the square of its distance from the particle. The first proposition considers the case when the particle is inside the sphere, the second when it is outside. The use of infinitesimals and limiting processes in geometrical constructions are simple and elegant and avoid the need for any integrations. They well illustrate Newton's method of proving many of the propositions in the ''Principia''. His proof of Propositions 70 is trivial. In the following, it is considered in slightly greater detail than Newton provides. The proof of Proposition 71 is more historically significant. It forms the first part of his proof that the gravitational force of a solid sphere acting on a particle outside it is inversely proportional to the square of its distance from the center of the sphere, provided the density at any point inside the sphere is a function only of its distance from the center of the sphere. Although the following are completely faithful to Newton's proofs, very minor changes have been made to attempt to make them clearer.Force on a point inside a hollow sphere
 Fig. 2 is a cross-section of the hollow sphere through the center, S and an arbitrary point, P, inside the sphere. Through P draw two lines IL and HK such that the angle KPL is very small. JM is the line through P that bisects that angle. From the geometry of circles, the triangles IPH and KPL are similar. The lines KH and IL are rotated about the axis JM to form 2 cones that intersect the sphere in 2 closed curves. In Fig. 1 the sphere is seen from a distance along the line PE and is assumed transparent so both curves can be seen.
The surface of the sphere that the cones intersect can be considered to be flat, and
Since the intersection of a cone with a plane is an ellipse, in this case the intersections form two ellipses with major axes IH and KL, where
By a similar argument, the minor axes are in the same ratio. This is clear if the sphere is viewed from above. Therefore the two ellipses are similar, so their areas are as the squares of their major axes. As the mass of any section of the surface is proportional to the area of that section, for the 2 elliptical areas the ratios of their masses
Since the force of attraction on P in the direction JM from either of the elliptic areas, is direct as the mass of the area and inversely as the square of its distance from P, it is independent of the distance of P from the sphere. Hence, the forces on P from the 2 infinitesimal elliptical areas are equal and opposite and there is no net force in the direction JM.
As the position of P and the direction of JM are both arbitrary, it follows that any particle inside a hollow sphere experiences no net force from the mass of the sphere.
Note: Newton simply describes the arcs IH and KL as 'minimally small' and the areas traced out by the lines IL and HK can be any shape, not necessarily elliptic, but they will always be similar.
Fig. 2 is a cross-section of the hollow sphere through the center, S and an arbitrary point, P, inside the sphere. Through P draw two lines IL and HK such that the angle KPL is very small. JM is the line through P that bisects that angle. From the geometry of circles, the triangles IPH and KPL are similar. The lines KH and IL are rotated about the axis JM to form 2 cones that intersect the sphere in 2 closed curves. In Fig. 1 the sphere is seen from a distance along the line PE and is assumed transparent so both curves can be seen.
The surface of the sphere that the cones intersect can be considered to be flat, and
Since the intersection of a cone with a plane is an ellipse, in this case the intersections form two ellipses with major axes IH and KL, where
By a similar argument, the minor axes are in the same ratio. This is clear if the sphere is viewed from above. Therefore the two ellipses are similar, so their areas are as the squares of their major axes. As the mass of any section of the surface is proportional to the area of that section, for the 2 elliptical areas the ratios of their masses
Since the force of attraction on P in the direction JM from either of the elliptic areas, is direct as the mass of the area and inversely as the square of its distance from P, it is independent of the distance of P from the sphere. Hence, the forces on P from the 2 infinitesimal elliptical areas are equal and opposite and there is no net force in the direction JM.
As the position of P and the direction of JM are both arbitrary, it follows that any particle inside a hollow sphere experiences no net force from the mass of the sphere.
Note: Newton simply describes the arcs IH and KL as 'minimally small' and the areas traced out by the lines IL and HK can be any shape, not necessarily elliptic, but they will always be similar.
Force on a point outside a hollow sphere
 Fig. 1 is a cross-section of the hollow sphere through the center, S with an arbitrary point, P, outside the sphere. PT is the tangent to the circle at T which passes through P. HI is a small arc on the surface such that PH is less than PT. Extend PI to intersect the sphere at L and draw SF to the point F that bisects IL. Extend PH to intersect the sphere at K and draw SE to the point E that bisects HK, and extend SF to intersect HK at D. Drop a perpendicular IQ on to the line PS joining P to the center S. Let the radius of the sphere be a and the distance PS be D.
Let arc IH be extended perpendicularly out of the plane of the diagram, by a small distance ζ. The area of the figure generated is and its mass is proportional to this product.
The force due to this mass on the particle at P and is along the line PI.
The component of this force towards the center .
If now the arc ''HI'' is rotated completely about the line ''PS'' to form a ring of width ''HI'' and radius ''IQ'', the length of the ring is 2·''IQ'' and its area is 2·''IQ''·''IH''. The component of the force due to this ring on the particle at ''P'' in the direction PS becomes
The perpendicular components of the force directed towards ''PS'' cancel out since the mass in the ring is distributed symmetrically about ''PS''. Therefore, the component in the direction ''PS'' is the total force on ''P'' due to the ring formed by rotating arc ''HI'' about ''PS''.
From similar triangles: and
If HI is sufficiently small that it can be taken as a straight line, is a right angle, and so that
Hence the force on ''P'' due to the ring
Assume now in Fig. 2 that another particle is outside the sphere at a point ''p'', a different distance ''d'' from the center of the sphere, with corresponding points lettered in lower case. For easy comparison, the construction of ''P'' in Fig. 1 is also shown in Fig. 2. As before, ''ph'' is less than ''pt''.
Generate a ring with width ih and radius iq by making angle and the slightly larger angle so that the distance PS is subtended by the same angle at I as is pS at i. The same holds for H and h, respectively.
The total force on p due to this ring is
:
Clearly and
Newton claims that DF and df can be taken as equal in the limit as the angles DPF and dpf 'vanish together'. Note that angles DPF and dpf are not equal. Although DS and dS become equal in the limit, this does not imply that the ratio of DF to df becomes equal to unity, when DF and df both approach zero. In the finite case DF depends on D, and df on d, so they are not equal.
Since the ratio of DF to df in the limit is crucial, more detailed analysis is required. From the similar right triangles, and giving Solving the quadratic for DF, in the limit as ES approaches FS, the smaller root, More simply, as DF approaches zero, in the limit the term can be ignored: leading to the same result. Clearly df has the same limit, justifying Newton’s claim.
Comparing the force from the ring HI rotated about PS to the ring hi about pS, the ratio of these 2 forces equals
By dividing up the arcs AT and Bt into corresponding infinitesimal rings, it follows that the ratio of the force due to the arc AT rotated about PS to that of Bt rotated about pS is in the same ratio, and similarly, the ratio of the forces due to arc TB to that of tA both rotated are in the same ratio.
Therefore, the force on a particle any distance D from the center of the hollow sphere is inversely proportional to which proves the proposition.
Fig. 1 is a cross-section of the hollow sphere through the center, S with an arbitrary point, P, outside the sphere. PT is the tangent to the circle at T which passes through P. HI is a small arc on the surface such that PH is less than PT. Extend PI to intersect the sphere at L and draw SF to the point F that bisects IL. Extend PH to intersect the sphere at K and draw SE to the point E that bisects HK, and extend SF to intersect HK at D. Drop a perpendicular IQ on to the line PS joining P to the center S. Let the radius of the sphere be a and the distance PS be D.
Let arc IH be extended perpendicularly out of the plane of the diagram, by a small distance ζ. The area of the figure generated is and its mass is proportional to this product.
The force due to this mass on the particle at P and is along the line PI.
The component of this force towards the center .
If now the arc ''HI'' is rotated completely about the line ''PS'' to form a ring of width ''HI'' and radius ''IQ'', the length of the ring is 2·''IQ'' and its area is 2·''IQ''·''IH''. The component of the force due to this ring on the particle at ''P'' in the direction PS becomes
The perpendicular components of the force directed towards ''PS'' cancel out since the mass in the ring is distributed symmetrically about ''PS''. Therefore, the component in the direction ''PS'' is the total force on ''P'' due to the ring formed by rotating arc ''HI'' about ''PS''.
From similar triangles: and
If HI is sufficiently small that it can be taken as a straight line, is a right angle, and so that
Hence the force on ''P'' due to the ring
Assume now in Fig. 2 that another particle is outside the sphere at a point ''p'', a different distance ''d'' from the center of the sphere, with corresponding points lettered in lower case. For easy comparison, the construction of ''P'' in Fig. 1 is also shown in Fig. 2. As before, ''ph'' is less than ''pt''.
Generate a ring with width ih and radius iq by making angle and the slightly larger angle so that the distance PS is subtended by the same angle at I as is pS at i. The same holds for H and h, respectively.
The total force on p due to this ring is
:
Clearly and
Newton claims that DF and df can be taken as equal in the limit as the angles DPF and dpf 'vanish together'. Note that angles DPF and dpf are not equal. Although DS and dS become equal in the limit, this does not imply that the ratio of DF to df becomes equal to unity, when DF and df both approach zero. In the finite case DF depends on D, and df on d, so they are not equal.
Since the ratio of DF to df in the limit is crucial, more detailed analysis is required. From the similar right triangles, and giving Solving the quadratic for DF, in the limit as ES approaches FS, the smaller root, More simply, as DF approaches zero, in the limit the term can be ignored: leading to the same result. Clearly df has the same limit, justifying Newton’s claim.
Comparing the force from the ring HI rotated about PS to the ring hi about pS, the ratio of these 2 forces equals
By dividing up the arcs AT and Bt into corresponding infinitesimal rings, it follows that the ratio of the force due to the arc AT rotated about PS to that of Bt rotated about pS is in the same ratio, and similarly, the ratio of the forces due to arc TB to that of tA both rotated are in the same ratio.
Therefore, the force on a particle any distance D from the center of the hollow sphere is inversely proportional to which proves the proposition.
Shell theorem in general relativity
An analogue for shell theorem exists ingeneral relativity
General relativity, also known as the general theory of relativity and Einstein's theory of gravity, is the geometric theory of gravitation published by Albert Einstein in 1915 and is the current description of gravitation in modern physics ...
(GR).
Spherical symmetry implies that the metric has time-independent Schwarzschild geometry, even if a central mass is undergoing gravitational collapse (Misner et al. 1973; see Birkhoff's theorem). The metric
Metric or metrical may refer to:
* Metric system, an internationally adopted decimal system of measurement
* An adjective indicating relation to measurement in general, or a noun describing a specific type of measurement
Mathematics
In mathem ...
thus has form
:
(using geometrized units, where For (where is the radius of some mass shell), mass acts as a delta function
In mathematics, the Dirac delta distribution ( distribution), also known as the unit impulse, is a generalized function or distribution over the real numbers, whose value is zero everywhere except at zero, and whose integral over the entire ...
at the origin. For shells of mass may exist externally, but for the metric to be non-singular
In the mathematical field of algebraic geometry, a singular point of an algebraic variety is a point that is 'special' (so, singular), in the geometric sense that at this point the tangent space at the variety may not be regularly defined. In ca ...
at the origin, must be zero in the metric. This reduces the metric to flat Minkowski space
In mathematical physics, Minkowski space (or Minkowski spacetime) () is a combination of three-dimensional Euclidean space and time into a four-dimensional manifold where the spacetime interval between any two events is independent of the iner ...
; thus external shells have no gravitational effect.
This result illuminates the gravitational collapse leading to a black hole and its effect on the motion of light-rays and particles outside and inside the event horizon (Hartle 2003, chapter 12).
See also
*Scale height
In atmospheric, earth, and planetary sciences, a scale height, usually denoted by the capital letter ''H'', is a distance ( vertical or radial) over which a physical quantity decreases by a factor of e (the base of natural logarithms, approxima ...
* Chasles' theorem (gravitation)
References
{{Reflist Gravity Physics theorems Mathematical theorems