Shannon–Fano–Elias coding on:
[Wikipedia]
[Google]
[Amazon]
In
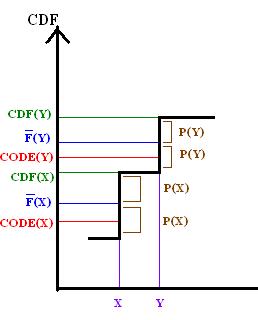 By definition of ''L'' it follows that
:
And because the bits after ''L''(''y'') are truncated from ''F''(''y'') to form code(''y''), it follows that
:
thus bcode(''y'') must be no less than CDF(''x'').
So the above graph demonstrates that the , therefore the prefix property holds.
By definition of ''L'' it follows that
:
And because the bits after ''L''(''y'') are truncated from ''F''(''y'') to form code(''y''), it follows that
:
thus bcode(''y'') must be no less than CDF(''x'').
So the above graph demonstrates that the , therefore the prefix property holds.
Thus for ''H''(''X''), the
information theory
Information theory is the mathematical study of the quantification (science), quantification, Data storage, storage, and telecommunications, communication of information. The field was established and formalized by Claude Shannon in the 1940s, ...
, Shannon–Fano–Elias coding is a precursor to arithmetic coding
Arithmetic coding (AC) is a form of entropy encoding used in lossless data compression. Normally, a String (computer science), string of characters is represented using a fixed number of bits per character, as in the American Standard Code for In ...
, in which probabilities are used to determine codewords.
It is named for Claude Shannon
Claude Elwood Shannon (April 30, 1916 – February 24, 2001) was an American mathematician, electrical engineer, computer scientist, cryptographer and inventor known as the "father of information theory" and the man who laid the foundations of th ...
, Robert Fano
Roberto Mario "Robert" Fano (11 November 1917 – 13 July 2016) was an Italian-American computer scientist and professor of electrical engineering and computer science at the Massachusetts Institute of Technology. He became a student and working ...
, and Peter Elias.
Algorithm description
Given adiscrete random variable
A random variable (also called random quantity, aleatory variable, or stochastic variable) is a mathematical formalization of a quantity or object which depends on random events. The term 'random variable' in its mathematical definition refers ...
''X'' of ordered values to be encoded, let be the probability for any ''x'' in ''X''. Define a function
:
Algorithm:
:For each ''x'' in ''X'',
::Let ''Z'' be the binary expansion of .
::Choose the length of the encoding of ''x'', , to be the integer
::Choose the encoding of ''x'', , be the first most significant bit
In computing, bit numbering is the convention used to identify the bit positions in a binary numeral system, binary number.
Bit significance and indexing
In computing, the least significant bit (LSb) is the bit position in a Binary numeral sy ...
s after the decimal point of ''Z''.
Example
Let ''X'' = , with probabilities ''p'' = . :For ''A'' :: ::In binary, ''Z''(''A'') = 0.0010101010... :: ::code(''A'') is 001 :For ''B'' :: ::In binary, ''Z''(''B'') = 0.01110101010101... :: ::code(''B'') is 011 :For ''C'' :: ::In binary, ''Z''(''C'') = 0.101010101010... :: ::code(''C'') is 1010 :For ''D'' :: ::In binary, Z(D) = 0.111 :: ::code(''D'') is 111Algorithm analysis
Prefix code
Shannon–Fano–Elias coding produces a binaryprefix code
A prefix code is a type of code system distinguished by its possession of the prefix property, which requires that there is no whole Code word (communication), code word in the system that is a prefix (computer science), prefix (initial segment) of ...
, allowing for direct decoding.
Let bcode(''x'') be the rational number formed by adding a decimal point before a binary code. For example, if code(''C'') = 1010 then bcode(''C'') = 0.1010. For all ''x'', if no ''y'' exists such that
:
then all the codes form a prefix code.
By comparing ''F'' to the CDF of ''X'', this property may be demonstrated graphically for Shannon–Fano–Elias coding.
 By definition of ''L'' it follows that
:
And because the bits after ''L''(''y'') are truncated from ''F''(''y'') to form code(''y''), it follows that
:
thus bcode(''y'') must be no less than CDF(''x'').
So the above graph demonstrates that the , therefore the prefix property holds.
By definition of ''L'' it follows that
:
And because the bits after ''L''(''y'') are truncated from ''F''(''y'') to form code(''y''), it follows that
:
thus bcode(''y'') must be no less than CDF(''x'').
So the above graph demonstrates that the , therefore the prefix property holds.
Code length
The average code length is .Thus for ''H''(''X''), the
entropy
Entropy is a scientific concept, most commonly associated with states of disorder, randomness, or uncertainty. The term and the concept are used in diverse fields, from classical thermodynamics, where it was first recognized, to the micros ...
of the random variable ''X'',
:
Shannon Fano Elias codes from 1 to 2 extra bits per symbol from ''X'' than entropy, so the code is not used in practice.
See also
*Shannon–Fano coding
In the field of data compression, Shannon–Fano coding, named after Claude Shannon and Robert Fano, is one of two related techniques for constructing a prefix code based on a set of symbols and their probabilities (estimated or measured).
* Shann ...
References
{{DEFAULTSORT:Shannon-Fano-Elias coding Lossless compression algorithms Data compression