Range (aeronautics)

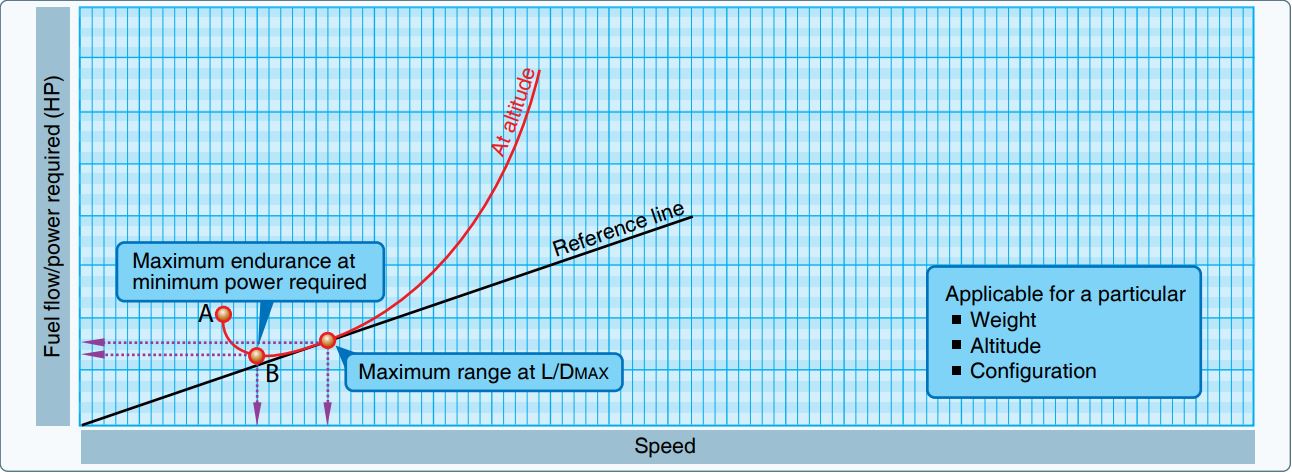The maximal total range is the maximum distance an aircraft can fly between takeoff and landing. Powered aircraft range is limited by the aviation fuel energy storage capacity (chemical or electrical) considering both weight and volume limits. Unpowered aircraft range depends on factors such as cross-country speed and environmental conditions. The range can be seen as the cross-country ground speed multiplied by the maximum time in the air. The fuel time limit for powered aircraft is fixed by the available fuel (considering reserve fuel requirements) and rate of consumption.

Some aircraft can gain energy while airborne through the environment (e.g. collecting solar energy or through rising air currents from mechanical or thermal lifting) or from in-flight refueling. These aircraft could theoretically have an infinite range.

Ferry range means the maximum range that an aircraft engaged in ferry flying can achieve. This usually means maximum fuel load, optionally with extra fuel tanks and minimum equipment. It refers to the transport of aircraft without any passengers or cargo.

'' Combat radius'' is a related measure based on the maximum distance a warplane can travel from its base of operations, accomplish some objective, and return to its original airfield with minimal reserves.

Derivation

For most unpowered aircraft, the maximum flight time is variable, limited by available daylight hours, aircraft design (performance), weather conditions, aircraft potential energy, and pilot endurance. Therefore, the range equation can only be calculated exactly for powered aircraft. It will be derived for both propeller and jet aircraft. If the total mass $W$ of the aircraft at a particular time $t$ is:
$W = W_0 + W_f,$
where $W_0$ is the zero-fuel mass and $W_f$ the mass of the fuel, the fuel consumption rate per unit time flow $F$ is equal to
$-\frac = -\frac.$

The rate of change of aircraft mass with distance $R$ is
$\frac = \frac = - \frac,$
where $V$ is the speed), so that
$\frac=-\frac$

It follows that the range is obtained from the definite integral below, with $t_1$ and $t_2$ the start and finish times respectively and $W_1$ and $W_2$ the initial and final aircraft masses

Specific range

The term $\frac$, where $V$ is the speed, and $F$ is the fuel consumption rate, is called the specific range (= range per unit mass of fuel; S.I. units: m/kg). The specific range can now be determined as though the airplane is in quasi-steady-state flight. Here, a difference between jet and propeller-driven aircraft has to be noticed.

Propeller aircraft

With propeller-driven propulsion, the level flight speed at a number of airplane weights from the equilibrium condition $P_a = P_r$ has to be noted. To each flight velocity, there corresponds a particular value of propulsive efficiency $\eta_j$ and specific fuel consumption $c_p$. The successive engine powers can be found:
$P_ = \frac$

The corresponding fuel weight flow rates can be computed now:
$F = c_p P_$

Thrust power is the speed multiplied by the drag, is obtained from the lift-to-drag ratio:
$P_a = V\frac Wg;$
here ''Wg'' is the weight (force in newtons, if ''W'' is the mass in kilograms); ''g'' is standard gravity (its exact value varies, but it averages 9.81 m/s²).

The range integral, assuming flight at a constant lift to drag ratio, becomes
$R = \frac \frac \int_^\frac$

To obtain an analytic expression for range, it has to be noted that specific range and fuel weight flow rate can be related to the characteristics of the airplane and propulsion system; if these are constant:
$R=\frac \frac \ln \frac$

Electric aircraft

An electric aircraft with battery power only will have the same mass at takeoff and landing. The logarithmic term with weight ratios is replaced by the direct ratio between $W_\text/W_\text$
$R=E^* \frac \eta_\text \frac \frac$
where $E^*$ is the energy per mass of the battery (e.g. 150-200 Wh/kg for Li-ion batteries), $\eta_\text$ the total efficiency (typically 0.7-0.8 for batteries, motor, gearbox and propeller), $L/D$ lift over drag (typically around 18), and the weight ratio $/$ typically around 0.3.https://www.mh-aerotools.de/company/paper_14/09%20-%20Electric%20Flight%20-%20Hepperle%20-%20DLR.pdf

Jet propulsion

The range of jet aircraft can be derived likewise. Now, quasi-steady level flight is assumed. The relationship $D = \fracW$ is used. The thrust can now be written as:
$T = D = \fracW ;$ here ''W'' is a force in newtons

Jet engines are characterized by a thrust specific fuel consumption, so that rate of fuel flow is proportional to drag, rather than power.

$F = c_T T = c_T\fracW$

Using the lift equation,
$\frac\rho V^2 S C_L = W$
where $\rho$ is the air density, and S the wing area, the specific range is found equal to:
$\frac = \frac \sqrt$

Inserting this into () and assuming only $W$ is varying, the range (in kilometers) becomes:
$R = \frac \sqrt\int_^\frac dW ;$
here $W$ is again mass.

When cruising at a fixed height, a fixed angle of attack and a constant specific fuel consumption, the range becomes:
$R = \frac \sqrt \left(\sqrt-\sqrt \right)$
where the compressibility on the aerodynamic characteristics of the airplane are neglected as the flight speed reduces during the flight.

Cruise/climb (Breguet range equation)

For jet aircraft operating in the stratosphere (altitude approximately between 11 and 20 km), the speed of sound is approximately constant, hence flying at a fixed angle of attack and constant Mach number requires the aircraft to climb (as weight decreases due to fuel burn), without changing the value of the local speed of sound. In this case:
$V = a M$
where $M$ is the cruise Mach number and $a$ the speed of sound. W is the weight. The range equation reduces to:
$R=\frac\frac\int_^\frac$
where $a= \sqrt$ ; here $R_s$is the specific heat constant of air (based on aviation standards) and $\gamma = 7/5 = 1.4$ (derived from $\gamma = \frac$ and $c_p = c_v+R_s$). $c_p$ and $c_v$ are the specific heat capacities of air at constant pressure and constant volume respectively.

Or $R = \frac \frac \ln\frac$, also known as the ''Breguet range equation'' after the French aviation pioneer, Breguet.

Modified Breguet range equation

It is possible to improve the accuracy of the Breguet range equation by recognizing the limitations of the conventionally used relationships for fuel flow:
$F = c_T T = c_T \frac W$

In the Breguet range equation, it is assumed that the thrust specific fuel consumption is constant as the aircraft weight decreases. This is generally not a good approximation because a significant portion (e.g. 5% to 10%) of the fuel flow does not produce thrust and is instead required for engine "accessories" such as hydraulic pumps, electrical generators, and bleed air powered cabin pressurization systems.

We can account for this by extending the assumed fuel flow formula in a simple way where an "adjusted" virtual aircraft gross weight $\widehat$ is defined by adding a constant additional "accessory" weight $W_\text$.

$\widehat = W + W_\text$
$F = \widehat _T \frac \widehat$

Here, the thrust specific fuel consumption has been adjusted down and the virtual aircraft weight has been adjusted up to maintain the proper fuel flow while making the adjusted thrust specific fuel consumption truly constant (not a function of virtual weight).

Then, the modified Breguet range equation becomes
$R = \frac\frac \ln\frac$

The above equation combines the energy characteristics of the fuel with the efficiency of the jet engine. It is often useful to separate these terms. Doing so completes the nondimensionalization of the range equation into fundamental design disciplines of aeronautics.

$R=Z_f\frac\frac\ln\frac$
where
* $Z_f$ is the geopotential energy height of the fuel (km)
* $\frac$ is the overall propulsive efficiency (nondimensional) $\eta_\text$
* $\frac$ is the aerodynamic efficiency (non-dimensional) $\eta_\text$
* $\ln\frac$ is the structural efficiency (non-dimensional) $\eta_\text$

giving the final form of the theoretical range equation (not including operational factors such as wind and routing)
$R = Z_f \eta_\text \eta_\text \eta_\text$

The geopotential energy height of the fuel is an intensive property. A physical interpretation is a height that a quantity of fuel could lift itself in the Earth's gravity field (assumed constant) by converting its chemical energy into potential energy. $Z_f$ for kerosene jet fuel is or 11% of the Earth's polar circumference. As an example, with an overall engine efficiency of 40%, a lift-to-drag ratio of 18:1, and a structural efficiency of 50%, the cruise range would be

Operational Considerations

The range equation may be further extended to consider operational factors by including an operational efficiency ("ops" for flight operations)
$R = Z_f \eta_\text \eta_\text \eta_\text \eta_\text$

The operational efficiency $\eta_$ may be expressed as the product of individual operational efficiency terms.
For example, average wind may be accounted for using the relationship between average GroundSpeed (GS), True AirSpeed (TAS, assumed constant), and average HeadWind (HW) component.

$\eta_\text = \frac=\frac$

Routing efficiency may be defined as the great-circle distance divided by the actual route distance
$\eta_\text = \frac$

Off-nominal temperatures may be accounted for with a temperature efficiency factor $\eta_\text$ (e.g. 99% at 10 deg C above International Standard Atmosphere (ISA) temperature)

All of the operational efficiency factors may be collected into a single term
$\eta_\text = \eta_\text \eta_\text \eta_\text \cdots$

See also

* Flight length
* Flight distance record
* Endurance
* Specific energy
* Geopotential height
* Energy conversion efficiency
* Jet engine performance
* Lift-to-drag ratio
* Fuel fraction, Mass ratio
* Newton's laws of motion

References

* G. J. J. Ruijgrok. ''Elements of Airplane Performance''. Delft University Press. .

Prof. Z. S. Spakovszky


' MIT turbines, 2002
* Martinez, Isidoro. http://imartinez.etsiae.upm.es/~isidoro/bk3/c17/Aircraft%20propulsion.pdf#page29 Aircraft propulsion. Range and endurance: Breguet's equation page 25.
* Marchman, James, III. (2021)
Aerodynamics and Aircraft Performance.
Blacksburg: VA: University Libraries at Virginia Tech. CC BY 4.0.
* David W. Anderson & Scott Eberhardt. ''Understanding Flight, Second Edition'' 2010 McGraw-Hill. (eBook) {{ISBN, 9780071626965 (print)

Aeronautics
Aircraft performance