Problem of Apollonius on:
[Wikipedia]
[Google]
[Amazon]

 In
In
Several other geometrical solutions to Apollonius' problem were developed in the 19th century. The most notable solutions are those of
and
 The solution of
The solution of  Instead of solving for the two hyperbolas, Newton constructs their directrix lines instead. For any hyperbola, the ratio of distances from a point Z to a focus A and to the directrix is a fixed constant called the
Instead of solving for the two hyperbolas, Newton constructs their directrix lines instead. For any hyperbola, the ratio of distances from a point Z to a focus A and to the directrix is a fixed constant called the
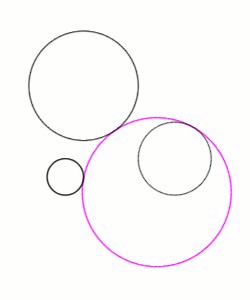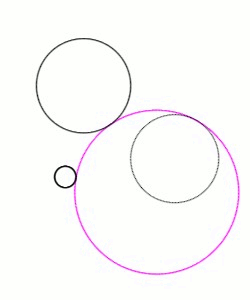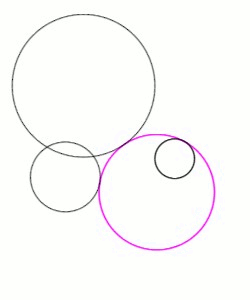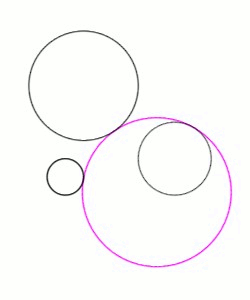 Viète began by solving the PPP case (three points) following the method of
Viète began by solving the PPP case (three points) following the method of
 A natural setting for problem of Apollonius is
A natural setting for problem of Apollonius is
 Solutions to Apollonius's problem generally occur in pairs; for each solution circle, there is a conjugate solution circle (Figure 6). One solution circle excludes the given circles that are enclosed by its conjugate solution, and vice versa. For example, in Figure 6, one solution circle (pink, upper left) encloses two given circles (black), but excludes a third; conversely, its conjugate solution (also pink, lower right) encloses that third given circle, but excludes the other two. The two conjugate solution circles are related by
Solutions to Apollonius's problem generally occur in pairs; for each solution circle, there is a conjugate solution circle (Figure 6). One solution circle excludes the given circles that are enclosed by its conjugate solution, and vice versa. For example, in Figure 6, one solution circle (pink, upper left) encloses two given circles (black), but excludes a third; conversely, its conjugate solution (also pink, lower right) encloses that third given circle, but excludes the other two. The two conjugate solution circles are related by
 When two of the given circles are concentric, Apollonius's problem can be solved easily using a method of
When two of the given circles are concentric, Apollonius's problem can be solved easily using a method of
 Gergonne's approach is to consider the solution circles in pairs. Let a pair of solution circles be denoted as ''C''A and ''C''B (the pink circles in Figure 6), and let their tangent points with the three given circles be denoted as A1, A2, A3, and B1, B2, B3, respectively. Gergonne's solution aims to locate these six points, and thus solve for the two solution circles.
Gergonne's insight was that if a line ''L''1 could be constructed such that A1 and B1 were guaranteed to fall on it, those two points could be identified as the intersection points of ''L''1 with the given circle ''C''1 (Figure 6). The remaining four tangent points would be located similarly, by finding lines ''L''2 and ''L''3 that contained A2 and B2, and A3 and B3, respectively. To construct a line such as ''L''1, two points must be identified that lie on it; but these points need not be the tangent points. Gergonne was able to identify two other points for each of the three lines. One of the two points has already been identified: the
Gergonne's approach is to consider the solution circles in pairs. Let a pair of solution circles be denoted as ''C''A and ''C''B (the pink circles in Figure 6), and let their tangent points with the three given circles be denoted as A1, A2, A3, and B1, B2, B3, respectively. Gergonne's solution aims to locate these six points, and thus solve for the two solution circles.
Gergonne's insight was that if a line ''L''1 could be constructed such that A1 and B1 were guaranteed to fall on it, those two points could be identified as the intersection points of ''L''1 with the given circle ''C''1 (Figure 6). The remaining four tangent points would be located similarly, by finding lines ''L''2 and ''L''3 that contained A2 and B2, and A3 and B3, respectively. To construct a line such as ''L''1, two points must be identified that lie on it; but these points need not be the tangent points. Gergonne was able to identify two other points for each of the three lines. One of the two points has already been identified: the  Gergonne found the radical axis ''R'' of the unknown solution circles as follows. Any pair of circles has two centers of similarity; these two points are the two possible intersections of two tangent lines to the two circles. Therefore, the three given circles have six centers of similarity, two for each distinct pair of given circles. Remarkably, these six points lie on four lines, three points on each line; moreover, each line corresponds to the
Gergonne found the radical axis ''R'' of the unknown solution circles as follows. Any pair of circles has two centers of similarity; these two points are the two possible intersections of two tangent lines to the two circles. Therefore, the three given circles have six centers of similarity, two for each distinct pair of given circles. Remarkably, these six points lie on four lines, three points on each line; moreover, each line corresponds to the
These limiting cases often have fewer solutions than the general problem; for example, the replacement of a given circle by a given point halves the number of solutions, since a point can be construed as an infinitesimal circle that is either internally or externally tangent.
 The problem of counting the number of solutions to different types of Apollonius' problem belongs to the field of
The problem of counting the number of solutions to different types of Apollonius' problem belongs to the field of
 Either Soddy circle, when taken together with the three given circles, produces a set of four circles that are mutually tangent at six points. The radii of these four circles are related by an equation known as Descartes' theorem. In a 1643 letter to Princess
Either Soddy circle, when taken together with the three given circles, produces a set of four circles that are mutually tangent at six points. The radii of these four circles are related by an equation known as Descartes' theorem. In a 1643 letter to Princess
MathWords online article
) and again in 1936 by
 Apollonius' problem can be extended from the plane to the
Apollonius' problem can be extended from the plane to the
which is higher than that of a regular (or rectifiable) curve (''d'' = 1) but less than that of a plane (''d'' = 2). The Apollonian gasket was first described by
Apollonius' problem can even be extended to ''d'' dimensions, to construct the
Euclidean plane geometry
Euclidean geometry is a mathematical system attributed to ancient Greek mathematician Euclid, which he described in his textbook on geometry: the '' Elements''. Euclid's approach consists in assuming a small set of intuitively appealing axio ...
, Apollonius's problem is to construct circles that are tangent
In geometry, the tangent line (or simply tangent) to a plane curve at a given point is the straight line that "just touches" the curve at that point. Leibniz defined it as the line through a pair of infinitely close points on the curve. Mo ...
to three given circles in a plane (Figure 1). Apollonius of Perga
Apollonius of Perga ( grc-gre, Ἀπολλώνιος ὁ Περγαῖος, Apollṓnios ho Pergaîos; la, Apollonius Pergaeus; ) was an Ancient Greek geometer and astronomer known for his work on conic sections. Beginning from the contributio ...
(c. 262 190 BC) posed and solved this famous problem in his work (', "Tangencies"); this work has been lost
Lost may refer to getting lost, or to:
Geography
* Lost, Aberdeenshire, a hamlet in Scotland
*Lake Okeechobee Scenic Trail, or LOST, a hiking and cycling trail in Florida, US
History
*Abbreviation of lost work, any work which is known to have bee ...
, but a 4th-century AD report of his results by Pappus of Alexandria
Pappus of Alexandria (; grc-gre, Πάππος ὁ Ἀλεξανδρεύς; AD) was one of the last great Greek mathematicians of antiquity known for his ''Synagoge'' (Συναγωγή) or ''Collection'' (), and for Pappus's hexagon theorem i ...
has survived. Three given circles generically have eight different circles that are tangent to them (Figure 2), a pair of solutions for each way to divide the three given circles in two subsets (there are 4 ways to divide a set of cardinality
In mathematics, the cardinality of a set is a measure of the number of elements of the set. For example, the set A = \ contains 3 elements, and therefore A has a cardinality of 3. Beginning in the late 19th century, this concept was generalized ...
3 in 2 parts).
In the 16th century, Adriaan van Roomen
Adriaan van Roomen (29 September 1561 – 4 May 1615), also known as Adrianus Romanus, was a mathematician, professor of medicine and medical astronomer from the Duchy of Brabant in the Habsburg Netherlands who was active throughout Central Europ ...
solved the problem using intersecting hyperbola
In mathematics, a hyperbola (; pl. hyperbolas or hyperbolae ; adj. hyperbolic ) is a type of smooth curve lying in a plane, defined by its geometric properties or by equations for which it is the solution set. A hyperbola has two pieces, ca ...
s, but this solution does not use only straightedge and compass
In geometry, straightedge-and-compass construction – also known as ruler-and-compass construction, Euclidean construction, or classical construction – is the construction of lengths, angles, and other geometric figures using only an ideal ...
constructions. François Viète
François Viète, Seigneur de la Bigotière ( la, Franciscus Vieta; 1540 – 23 February 1603), commonly know by his mononym, Vieta, was a French mathematician whose work on new algebra was an important step towards modern algebra, due to i ...
found such a solution by exploiting limiting cases: any of the three given circles can be shrunk to zero radius (a point) or expanded to infinite radius (a line). Viète's approach, which uses simpler limiting cases to solve more complicated ones, is considered a plausible reconstruction of Apollonius' method. The method of van Roomen was simplified by Isaac Newton
Sir Isaac Newton (25 December 1642 – 20 March 1726/27) was an English mathematician, physicist, astronomer, alchemist, Theology, theologian, and author (described in his time as a "natural philosophy, natural philosopher"), widely ...
, who showed that Apollonius' problem is equivalent to finding a position from the differences of its distances to three known points. This has applications in navigation and positioning systems such as LORAN
LORAN, short for long range navigation, was a hyperbolic radio navigation system developed in the United States during World War II. It was similar to the UK's Gee system but operated at lower frequencies in order to provide an improved range ...
.
Later mathematicians introduced algebraic methods, which transform a geometric problem into algebraic equations. These methods were simplified by exploiting symmetries inherent in the problem of Apollonius: for instance solution circles generically occur in pairs, with one solution enclosing the given circles that the other excludes (Figure 2). Joseph Diaz Gergonne
Joseph Diez Gergonne (19 June 1771 at Nancy, France – 4 May 1859 at Montpellier, France) was a French mathematician and logician.
Life
In 1791, Gergonne enlisted in the French army as a captain. That army was undergoing rapid expansion becau ...
used this symmetry to provide an elegant straightedge and compass solution, while other mathematicians used geometrical transformations such as reflection in a circle to simplify the configuration of the given circles. These developments provide a geometrical setting for algebraic methods (using Lie sphere geometry) and a classification of solutions according to 33 essentially different configurations of the given circles.
Apollonius' problem has stimulated much further work. Generalizations to three dimensions—constructing a sphere tangent to four given spheres—and beyond
Beyond may refer to:
Arts, entertainment, and media
Films
* ''Beyond'' (1921 film), an American silent film
* ''Beyond'' (2000 film), a Danish film directed by Åke Sandgren, OT: ''Dykkerne''
* ''Beyond'' (2010 film), a Swedish film directed ...
have been studied. The configuration of three mutually tangent circles has received particular attention. René Descartes
René Descartes ( or ; ; Latinized: Renatus Cartesius; 31 March 1596 – 11 February 1650) was a French philosopher, scientist, and mathematician, widely considered a seminal figure in the emergence of modern philosophy and science. Ma ...
gave a formula relating the radii of the solution circles and the given circles, now known as Descartes' theorem. Solving Apollonius' problem iteratively in this case leads to the Apollonian gasket
In mathematics, an Apollonian gasket or Apollonian net is a fractal generated by starting with a triple of circles, each tangent to the other two, and successively filling in more circles, each tangent to another three. It is named after Greek ...
, which is one of the earliest fractal
In mathematics, a fractal is a geometric shape containing detailed structure at arbitrarily small scales, usually having a fractal dimension strictly exceeding the topological dimension. Many fractals appear similar at various scales, as ill ...
s to be described in print, and is important in number theory
Number theory (or arithmetic or higher arithmetic in older usage) is a branch of pure mathematics devoted primarily to the study of the integers and integer-valued functions. German mathematician Carl Friedrich Gauss (1777–1855) said, "Ma ...
via Ford circles and the Hardy–Littlewood circle method.
Statement of the problem
The general statement of Apollonius' problem is to construct one or more circles that are tangent to three given objects in a plane, where an object may be a line, a point or a circle of any size. These objects may be arranged in any way and may cross one another; however, they are usually taken to be distinct, meaning that they do not coincide. Solutions to Apollonius' problem are sometimes called ''Apollonius circles'', although the term is also used for other types of circles associated with Apollonius. The property of tangency is defined as follows. First, a point, line or circle is assumed to be tangent to itself; hence, if a given circle is already tangent to the other two given objects, it is counted as a solution to Apollonius' problem. Two distinct geometrical objects are said to ''intersect'' if they have a point in common. By definition, a point is tangent to a circle or a line if it intersects them, that is, if it lies on them; thus, two distinct points cannot be tangent. If the angle between lines or circles at an intersection point is zero, they are said to be ''tangent''; the intersection point is called a ''tangent point'' or a ''point of tangency''. (The word "tangent" derives from theLatin
Latin (, or , ) is a classical language belonging to the Italic languages, Italic branch of the Indo-European languages. Latin was originally a dialect spoken in the lower Tiber area (then known as Latium) around present-day Rome, but through ...
present participle
In linguistics, a participle () (from Latin ' a "sharing, partaking") is a nonfinite verb form that has some of the characteristics and functions of both verbs and adjectives. More narrowly, ''participle'' has been defined as "a word derived fro ...
, ''tangens'', meaning "touching".) In practice, two distinct circles are tangent if they intersect at only one point; if they intersect at zero or two points, they are not tangent. The same holds true for a line and a circle. Two distinct lines cannot be tangent in the plane, although two parallel
Parallel is a geometric term of location which may refer to:
Computing
* Parallel algorithm
* Parallel computing
* Parallel metaheuristic
* Parallel (software), a UNIX utility for running programs in parallel
* Parallel Sysplex, a cluster o ...
lines can be considered as tangent at a point at infinity
In geometry, a point at infinity or ideal point is an idealized limiting point at the "end" of each line.
In the case of an affine plane (including the Euclidean plane), there is one ideal point for each pencil of parallel lines of the plane. ...
in inversive geometry
Inversive activities are processes which self internalise the action concerned. For example, a person who has an Inversive personality internalises his emotion
Emotions are mental states brought on by neurophysiological changes, variou ...
(see below
Below may refer to:
*Earth
* Ground (disambiguation)
*Soil
*Floor
* Bottom (disambiguation)
*Less than
*Temperatures below freezing
*Hell or underworld
People with the surname
*Ernst von Below (1863–1955), German World War I general
*Fred Below ...
).
The solution circle may be either internally or externally tangent to each of the given circles. An ''external'' tangency is one where the two circles bend away from each other at their point of contact; they lie on opposite sides of the tangent line
In geometry, the tangent line (or simply tangent) to a plane curve at a given point is the straight line that "just touches" the curve at that point. Leibniz defined it as the line through a pair of infinitely close points on the curve. Mo ...
at that point, and they exclude one another. The distance between their centers equals the sum of their radii. By contrast, an ''internal'' tangency is one in which the two circles curve in the same way at their point of contact; the two circles lie on the same side of the tangent line, and one circle encloses the other. In this case, the distance between their centers equals the difference of their radii. As an illustration, in Figure 1, the pink solution circle is internally tangent to the medium-sized given black circle on the right, whereas it is externally tangent to the smallest and largest given circles on the left.
Apollonius' problem can also be formulated as the problem of locating one or more points such that the ''differences'' of its distances to three given points equal three known values. Consider a solution circle of radius ''r''''s'' and three given circles of radii ''r''1, ''r''2 and ''r''3. If the solution circle is externally tangent to all three given circles, the distances between the center of the solution circle and the centers of the given circles equal , and , respectively. Therefore, differences in these distances are constants, such as ; they depend only on the known radii of the given circles and not on the radius ''r''''s'' of the solution circle, which cancels out. This second formulation of Apollonius' problem can be generalized to internally tangent solution circles (for which the center-center distance equals the difference of radii), by changing the corresponding differences of distances to sums of distances, so that the solution-circle radius ''r''''s'' again cancels out. The re-formulation in terms of center-center distances is useful in the solutions below of Adriaan van Roomen
Adriaan van Roomen (29 September 1561 – 4 May 1615), also known as Adrianus Romanus, was a mathematician, professor of medicine and medical astronomer from the Duchy of Brabant in the Habsburg Netherlands who was active throughout Central Europ ...
and Isaac Newton
Sir Isaac Newton (25 December 1642 – 20 March 1726/27) was an English mathematician, physicist, astronomer, alchemist, Theology, theologian, and author (described in his time as a "natural philosophy, natural philosopher"), widely ...
, and also in hyperbolic positioning or trilateration, which is the task of locating a position from differences in distances to three known points. For example, navigation systems such as LORAN
LORAN, short for long range navigation, was a hyperbolic radio navigation system developed in the United States during World War II. It was similar to the UK's Gee system but operated at lower frequencies in order to provide an improved range ...
identify a receiver's position from the differences in arrival times of signals from three fixed positions, which correspond to the differences in distances to those transmitters.
History
A rich repertoire of geometrical and algebraic methods have been developed to solve Apollonius' problem, which has been called "the most famous of all" geometry problems. The original approach ofApollonius of Perga
Apollonius of Perga ( grc-gre, Ἀπολλώνιος ὁ Περγαῖος, Apollṓnios ho Pergaîos; la, Apollonius Pergaeus; ) was an Ancient Greek geometer and astronomer known for his work on conic sections. Beginning from the contributio ...
has been lost, but reconstructions have been offered by François Viète
François Viète, Seigneur de la Bigotière ( la, Franciscus Vieta; 1540 – 23 February 1603), commonly know by his mononym, Vieta, was a French mathematician whose work on new algebra was an important step towards modern algebra, due to i ...
and others, based on the clues in the description by Pappus of Alexandria
Pappus of Alexandria (; grc-gre, Πάππος ὁ Ἀλεξανδρεύς; AD) was one of the last great Greek mathematicians of antiquity known for his ''Synagoge'' (Συναγωγή) or ''Collection'' (), and for Pappus's hexagon theorem i ...
. The first new solution method was published in 1596 by Adriaan van Roomen
Adriaan van Roomen (29 September 1561 – 4 May 1615), also known as Adrianus Romanus, was a mathematician, professor of medicine and medical astronomer from the Duchy of Brabant in the Habsburg Netherlands who was active throughout Central Europ ...
, who identified the centers of the solution circles as the intersection points of two hyperbola
In mathematics, a hyperbola (; pl. hyperbolas or hyperbolae ; adj. hyperbolic ) is a type of smooth curve lying in a plane, defined by its geometric properties or by equations for which it is the solution set. A hyperbola has two pieces, ca ...
s. Van Roomen's method was refined in 1687 by Isaac Newton
Sir Isaac Newton (25 December 1642 – 20 March 1726/27) was an English mathematician, physicist, astronomer, alchemist, Theology, theologian, and author (described in his time as a "natural philosophy, natural philosopher"), widely ...
in his '' Principia'', and by John Casey in 1881.
Although successful in solving Apollonius' problem, van Roomen's method has a drawback. A prized property in classical Euclidean geometry
Euclidean geometry is a mathematical system attributed to ancient Greek mathematician Euclid, which he described in his textbook on geometry: the '' Elements''. Euclid's approach consists in assuming a small set of intuitively appealing axioms ...
is the ability to solve problems using only a compass and a straightedge. Many constructions are impossible using only these tools, such as dividing an angle in three equal parts. However, many such "impossible" problems can be solved by intersecting curves such as hyperbolas, ellipse
In mathematics, an ellipse is a plane curve surrounding two focal points, such that for all points on the curve, the sum of the two distances to the focal points is a constant. It generalizes a circle, which is the special type of ellipse in ...
s and parabola
In mathematics, a parabola is a plane curve which is mirror-symmetrical and is approximately U-shaped. It fits several superficially different mathematical descriptions, which can all be proved to define exactly the same curves.
One descri ...
s (conic section
In mathematics, a conic section, quadratic curve or conic is a curve obtained as the intersection of the surface of a cone with a plane. The three types of conic section are the hyperbola, the parabola, and the ellipse; the circle is a ...
s). For example, doubling the cube
Doubling the cube, also known as the Delian problem, is an ancient geometric problem. Given the edge of a cube, the problem requires the construction of the edge of a second cube whose volume is double that of the first. As with the related probl ...
(the problem of constructing a cube of twice the volume of a given cube) cannot be done using only a straightedge and compass, but Menaechmus :''There is also a Menaechmus in Plautus' play, ''The Menaechmi''.''
Menaechmus ( el, Μέναιχμος, 380–320 BC) was an ancient Greek mathematician, geometer and philosopher born in Alopeconnesus or Prokonnesos in the Thracian Chersones ...
showed that the problem can be solved by using the intersections of two parabola
In mathematics, a parabola is a plane curve which is mirror-symmetrical and is approximately U-shaped. It fits several superficially different mathematical descriptions, which can all be proved to define exactly the same curves.
One descri ...
s. Therefore, van Roomen's solution—which uses the intersection of two hyperbolas—did not determine if the problem satisfied the straightedge-and-compass property.
Van Roomen's friend François Viète
François Viète, Seigneur de la Bigotière ( la, Franciscus Vieta; 1540 – 23 February 1603), commonly know by his mononym, Vieta, was a French mathematician whose work on new algebra was an important step towards modern algebra, due to i ...
, who had urged van Roomen to work on Apollonius' problem in the first place, developed a method that used only compass and straightedge. Prior to Viète's solution, Regiomontanus
Johannes Müller von Königsberg (6 June 1436 – 6 July 1476), better known as Regiomontanus (), was a mathematician, astrologer and astronomer of the German Renaissance, active in Vienna, Buda and Nuremberg. His contributions were instrument ...
doubted whether Apollonius' problem could be solved by straightedge and compass. Viète first solved some simple special cases of Apollonius' problem, such as finding a circle that passes through three given points which has only one solution if the points are distinct; he then built up to solving more complicated special cases, in some cases by shrinking or swelling the given circles. According to the 4th-century report of Pappus, Apollonius' own book on this problem—entitled (', "Tangencies"; Latin: ''De tactionibus'', ''De contactibus'')—followed a similar progressive approach. Hence, Viète's solution is considered to be a plausible reconstruction of Apollonius' solution, although other reconstructions have been published independently by three different authors. Simson R (1734) ''Mathematical Collection'', volume VII, p. 117.Several other geometrical solutions to Apollonius' problem were developed in the 19th century. The most notable solutions are those of
Jean-Victor Poncelet
Jean-Victor Poncelet (; 1 July 1788 – 22 December 1867) was a French engineer and mathematician who served most notably as the Commanding General of the École Polytechnique. He is considered a reviver of projective geometry, and his work '' ...
(1811) and of Joseph Diaz Gergonne
Joseph Diez Gergonne (19 June 1771 at Nancy, France – 4 May 1859 at Montpellier, France) was a French mathematician and logician.
Life
In 1791, Gergonne enlisted in the French army as a captain. That army was undergoing rapid expansion becau ...
(1814). Whereas Poncelet's proof relies on homothetic centers of circles and the power of a point
In elementary plane geometry, the power of a point is a real number that reflects the relative distance of a given point from a given circle. It was introduced by Jakob Steiner in 1826.
Specifically, the power \Pi(P) of a point P with respect ...
theorem, Gergonne's method exploits the conjugate relation between lines and their poles
Poles,, ; singular masculine: ''Polak'', singular feminine: ''Polka'' or Polish people, are a West Slavic nation and ethnic group, who share a common history, culture, the Polish language and are identified with the country of Poland in ...
in a circle. Methods using circle inversion
A circle is a shape consisting of all points in a plane that are at a given distance from a given point, the centre. Equivalently, it is the curve traced out by a point that moves in a plane so that its distance from a given point is const ...
were pioneered by Julius Petersen
Julius Peter Christian Petersen (16 June 1839, Sorø, West Zealand – 5 August 1910, Copenhagen) was a Danish mathematician. His contributions to the field of mathematics led to the birth of graph theory.
Biography
Petersen's interest ...
in 1879; one example is the annular solution method of HSM Coxeter. Another approach uses Lie sphere geometry, which was developed by Sophus Lie
Marius Sophus Lie ( ; ; 17 December 1842 – 18 February 1899) was a Norwegian mathematician. He largely created the theory of continuous symmetry and applied it to the study of geometry and differential equations.
Life and career
Marius S ...
.
Algebraic solutions to Apollonius' problem were pioneered in the 17th century by René Descartes
René Descartes ( or ; ; Latinized: Renatus Cartesius; 31 March 1596 – 11 February 1650) was a French philosopher, scientist, and mathematician, widely considered a seminal figure in the emergence of modern philosophy and science. Ma ...
and Princess Elisabeth of Bohemia
Elisabeth of the Palatinate (26 December 1618 – 11 February 1680), also known as Elisabeth of Bohemia, Princess Elisabeth of the Palatinate, or Princess-Abbess of Herford Abbey, was the eldest daughter of Frederick V, Elector Palatine (who was b ...
, although their solutions were rather complex. Practical algebraic methods were developed in the late 18th and 19th centuries by several mathematicians, including Leonhard Euler
Leonhard Euler ( , ; 15 April 170718 September 1783) was a Swiss mathematician, physicist, astronomer, geographer, logician and engineer who founded the studies of graph theory and topology and made pioneering and influential discoveries ...
, Nicolas Fuss
Nicolas Fuss (29 January 1755 – 4 January 1826), also known as Nikolai Fuss, was a Swiss mathematician, living most of his life in Imperial Russia.
Biography
Fuss was born in Basel, Switzerland. He moved to Saint Petersburg to serve as a mat ...
, Carl Friedrich Gauss
Johann Carl Friedrich Gauss (; german: Gauß ; la, Carolus Fridericus Gauss; 30 April 177723 February 1855) was a German mathematician and physicist who made significant contributions to many fields in mathematics and science. Sometimes refer ...
, Lazare Carnot
Lazare Nicolas Marguerite, Count Carnot (; 13 May 1753 – 2 August 1823) was a French mathematician, physicist and politician. He was known as the "Organizer of Victory" in the French Revolutionary Wars and Napoleonic Wars.
Education and early ...
,and
Augustin Louis Cauchy
Baron Augustin-Louis Cauchy (, ; ; 21 August 178923 May 1857) was a French mathematician, engineer, and physicist who made pioneering contributions to several branches of mathematics, including mathematical analysis and continuum mechanics. He w ...
.
Solution methods
Intersecting hyperbolas
Adriaan van Roomen
Adriaan van Roomen (29 September 1561 – 4 May 1615), also known as Adrianus Romanus, was a mathematician, professor of medicine and medical astronomer from the Duchy of Brabant in the Habsburg Netherlands who was active throughout Central Europ ...
(1596) is based on the intersection of two hyperbola
In mathematics, a hyperbola (; pl. hyperbolas or hyperbolae ; adj. hyperbolic ) is a type of smooth curve lying in a plane, defined by its geometric properties or by equations for which it is the solution set. A hyperbola has two pieces, ca ...
s. Let the given circles be denoted as ''C''1, ''C''2 and ''C''3. Van Roomen solved the general problem by solving a simpler problem, that of finding the circles that are tangent to ''two'' given circles, such as ''C''1 and ''C''2. He noted that the center of a circle tangent to both given circles must lie on a hyperbola
In mathematics, a hyperbola (; pl. hyperbolas or hyperbolae ; adj. hyperbolic ) is a type of smooth curve lying in a plane, defined by its geometric properties or by equations for which it is the solution set. A hyperbola has two pieces, ca ...
whose foci are the centers of the given circles. To understand this, let the radii of the solution circle and the two given circles be denoted as ''r''''s'', ''r''''1'' and ''r''''2'', respectively (Figure 3). The distance ''d''1 between the centers of the solution circle and ''C''1 is either or , depending on whether these circles are chosen to be externally or internally tangent, respectively. Similarly, the distance ''d''2 between the centers of the solution circle and ''C''2 is either or , again depending on their chosen tangency. Thus, the difference between these distances is always a constant that is independent of ''r''''s''. This property, of having a fixed difference between the distances to the foci, characterizes hyperbolas, so the possible centers of the solution circle lie on a hyperbola. A second hyperbola can be drawn for the pair of given circles ''C''2 and ''C''3, where the internal or external tangency of the solution and ''C''2 should be chosen consistently with that of the first hyperbola. An intersection of these two hyperbolas (if any) gives the center of a solution circle that has the chosen internal and external tangencies to the three given circles. The full set of solutions to Apollonius' problem can be found by considering all possible combinations of internal and external tangency of the solution circle to the three given circles.
Isaac Newton
Sir Isaac Newton (25 December 1642 – 20 March 1726/27) was an English mathematician, physicist, astronomer, alchemist, Theology, theologian, and author (described in his time as a "natural philosophy, natural philosopher"), widely ...
(1687) refined van Roomen's solution, so that the solution-circle centers were located at the intersections of a line with a circle. Newton formulates Apollonius' problem as a problem in trilateration Trilateration is the use of distances (or "ranges") for determining the unknown position coordinates of a point of interest, often around Earth (geopositioning).
When more than three distances are involved, it may be called multilateration, for e ...
: to locate a point Z from three given points A, B and C, such that the differences in distances from Z to the three given points have known values. These four points correspond to the center of the solution circle (Z) and the centers of the three given circles (A, B and C).
eccentricity
Eccentricity or eccentric may refer to:
* Eccentricity (behavior), odd behavior on the part of a person, as opposed to being "normal"
Mathematics, science and technology Mathematics
* Off-Centre (geometry), center, in geometry
* Eccentricity (g ...
. The two directrices intersect at a point T, and from their two known distance ratios, Newton constructs a line passing through T on which Z must lie. However, the ratio of distances TZ/TA is also known; hence, Z also lies on a known circle, since Apollonius had shown that a circle
A circle is a shape consisting of all points in a plane that are at a given distance from a given point, the centre. Equivalently, it is the curve traced out by a point that moves in a plane so that its distance from a given point is cons ...
can be defined as the set of points that have a given ratio of distances to two fixed points. (As an aside, this definition is the basis of bipolar coordinates.) Thus, the solutions to Apollonius' problem are the intersections of a line with a circle.
Viète's reconstruction
As describedbelow
Below may refer to:
*Earth
*Ground (disambiguation)
*Soil
*Floor
*Bottom (disambiguation)
*Less than
*Temperatures below freezing
*Hell or underworld
People with the surname
*Ernst von Below (1863–1955), German World War I general
*Fred Below ( ...
, Apollonius' problem has ten special cases, depending on the nature of the three given objects, which may be a circle (C), line (L) or point (P). By custom, these ten cases are distinguished by three letter codes such as CCP. Viète solved all ten of these cases using only compass and straightedge constructions, and used the solutions of simpler cases to solve the more complex cases.
 Viète began by solving the PPP case (three points) following the method of
Viète began by solving the PPP case (three points) following the method of Euclid
Euclid (; grc-gre, Εὐκλείδης; BC) was an ancient Greek mathematician active as a geometer and logician. Considered the "father of geometry", he is chiefly known for the '' Elements'' treatise, which established the foundations of ...
in his '' Elements''. From this, he derived a lemma
Lemma may refer to:
Language and linguistics
* Lemma (morphology), the canonical, dictionary or citation form of a word
* Lemma (psycholinguistics), a mental abstraction of a word about to be uttered
Science and mathematics
* Lemma (botany), ...
corresponding to the power of a point
In elementary plane geometry, the power of a point is a real number that reflects the relative distance of a given point from a given circle. It was introduced by Jakob Steiner in 1826.
Specifically, the power \Pi(P) of a point P with respect ...
theorem, which he used to solve the LPP case (a line and two points). Following Euclid a second time, Viète solved the LLL case (three lines) using the angle bisectors
In geometry, bisection is the division of something into two equal or congruent parts, usually by a line, which is then called a ''bisector''. The most often considered types of bisectors are the ''segment bisector'' (a line that passes throug ...
. He then derived a lemma for constructing the line perpendicular to an angle bisector that passes through a point, which he used to solve the LLP problem (two lines and a point). This accounts for the first four cases of Apollonius' problem, those that do not involve circles.
To solve the remaining problems, Viète exploited the fact that the given circles and the solution circle may be re-sized in tandem while preserving their tangencies (Figure 4). If the solution-circle radius is changed by an amount Δ''r'', the radius of its internally tangent given circles must be likewise changed by Δ''r'', whereas the radius of its externally tangent given circles must be changed by −Δ''r''. Thus, as the solution circle swells, the internally tangent given circles must swell in tandem, whereas the externally tangent given circles must shrink, to maintain their tangencies.
Viète used this approach to shrink one of the given circles to a point, thus reducing the problem to a simpler, already solved case. He first solved the CLL case (a circle and two lines) by shrinking the circle into a point, rendering it an LLP case. He then solved the CLP case (a circle, a line and a point) using three lemmas. Again shrinking one circle to a point, Viète transformed the CCL case into a CLP case. He then solved the CPP case (a circle and two points) and the CCP case (two circles and a point), the latter case by two lemmas. Finally, Viète solved the general CCC case (three circles) by shrinking one circle to a point, rendering it a CCP case.
Algebraic solutions
Apollonius' problem can be framed as a system of three equations for the center and radius of the solution circle. Since the three given circles and any solution circle must lie in the same plane, their positions can be specified in terms of the (''x'', ''y'')coordinates
In geometry, a coordinate system is a system that uses one or more numbers, or coordinates, to uniquely determine the position of the points or other geometric elements on a manifold such as Euclidean space. The order of the coordinates is sig ...
of their centers. For example, the center positions of the three given circles may be written as (''x''1, ''y''1), (''x''2, ''y''2) and (''x''3, ''y''3), whereas that of a solution circle can be written as (''x''''s'', ''y''''s''). Similarly, the radii of the given circles and a solution circle can be written as ''r''1, ''r''2, ''r''3 and ''r''''s'', respectively. The requirement that a solution circle must exactly touch each of the three given circles can be expressed as three coupled
''Coupled'' is an American dating game show that aired on Fox from May 17 to August 2, 2016. It was hosted by television personality, Terrence J and created by Mark Burnett, of '' Survivor'', ''The Apprentice'', '' Are You Smarter Than a 5th G ...
quadratic equation
In algebra, a quadratic equation () is any equation that can be rearranged in standard form as
ax^2 + bx + c = 0\,,
where represents an unknown value, and , , and represent known numbers, where . (If and then the equation is linear, not qu ...
s for ''x''''s'', ''y''''s'' and ''r''''s'':
:
:
:
The three numbers ''s''1, ''s''2 and ''s''3 on the right-hand side
In mathematics, LHS is informal shorthand for the left-hand side of an equation. Similarly, RHS is the right-hand side. The two sides have the same value, expressed differently, since equality is symmetric.resultant
In mathematics, the resultant of two polynomials is a polynomial expression of their coefficients, which is equal to zero if and only if the polynomials have a common root (possibly in a field extension), or, equivalently, a common factor (ov ...
s. When multiplied out, all three equations have on the left-hand side, and ''r''''s''2 on the right-hand side. Subtracting one equation from another eliminates these quadratic terms; the remaining linear terms may be re-arranged to yield formulae for the coordinates ''x''''s'' and ''y''''s''
:
:
where ''M'', ''N'', ''P'' and ''Q'' are known functions of the given circles and the choice of signs. Substitution of these formulae into one of the initial three equations gives a quadratic equation for ''r''''s'', which can be solved by the quadratic formula
In elementary algebra, the quadratic formula is a formula that provides the solution(s) to a quadratic equation. There are other ways of solving a quadratic equation instead of using the quadratic formula, such as factoring (direct factoring, ...
. Substitution of the numerical value of ''r''''s'' into the linear formulae yields the corresponding values of ''x''''s'' and ''y''''s''.
The signs ''s''1, ''s''2 and ''s''3 on the right-hand sides of the equations may be chosen in eight possible ways, and each choice of signs gives up to two solutions, since the equation for ''r''''s'' is quadratic. This might suggest (incorrectly) that there are up to sixteen solutions of Apollonius' problem. However, due to a symmetry of the equations, if (''r''''s'', ''x''''s'', ''y''''s'') is a solution, with signs ''s''''i'', then so is (−''r''''s'', ''x''''s'', ''y''''s''), with opposite signs −''s''''i'', which represents the same solution circle. Therefore, Apollonius' problem has at most eight independent solutions (Figure 2). One way to avoid this double-counting is to consider only solution circles with non-negative radius.
The two roots of any quadratic equation may be of three possible types: two different real number
In mathematics, a real number is a number that can be used to measure a ''continuous'' one-dimensional quantity such as a distance, duration or temperature. Here, ''continuous'' means that values can have arbitrarily small variations. Every ...
s, two identical real numbers (i.e., a degenerate double root), or a pair of complex conjugate
In mathematics, the complex conjugate of a complex number is the number with an equal real part and an imaginary part equal in magnitude but opposite in sign. That is, (if a and b are real, then) the complex conjugate of a + bi is equal to a - ...
roots. The first case corresponds to the usual situation; each pair of roots corresponds to a pair of solutions that are related by circle inversion
A circle is a shape consisting of all points in a plane that are at a given distance from a given point, the centre. Equivalently, it is the curve traced out by a point that moves in a plane so that its distance from a given point is const ...
, as described below (Figure 6). In the second case, both roots are identical, corresponding to a solution circle that transforms into itself under inversion. In this case, one of the given circles is itself a solution to the Apollonius problem, and the number of distinct solutions is reduced by one. The third case of complex conjugate radii does not correspond to a geometrically possible solution for Apollonius' problem, since a solution circle cannot have an imaginary radius; therefore, the number of solutions is reduced by two. Apollonius' problem cannot have seven solutions, although it may have any other number of solutions from zero to eight.
Lie sphere geometry
The same algebraic equations can be derived in the context of Lie sphere geometry. That geometry represents circles, lines and points in a unified way, as a five-dimensional vector ''X'' = (''v'', ''c''''x'', ''c''''y'', ''w'', ''sr''), where c = (''c''''x'', ''c''''y'') is the center of the circle, and ''r'' is its (non-negative) radius. If ''r'' is not zero, the sign ''s'' may be positive or negative; for visualization, ''s'' represents the orientation of the circle, with counterclockwise circles having a positive ''s'' and clockwise circles having a negative ''s''. The parameter ''w'' is zero for a straight line, and one otherwise. In this five-dimensional world, there is a bilinear product similar to thedot product
In mathematics, the dot product or scalar productThe term ''scalar product'' means literally "product with a scalar as a result". It is also used sometimes for other symmetric bilinear forms, for example in a pseudo-Euclidean space. is an alg ...
:
:
The Lie quadric is defined as those vectors whose product with themselves (their square norm) is zero, (''X'', ''X'') = 0. Let ''X''1 and ''X''2 be two vectors belonging to this quadric; the norm of their difference equals
:
The product distributes over addition and subtraction (more precisely, it is bilinear):
:
Since (''X''1, ''X''1) = (''X''2, ''X''2) = 0 (both belong to the Lie quadric) and since ''w''1 = ''w''2 = 1 for circles, the product of any two such vectors on the quadric equals
:
where the vertical bars sandwiching represent the length of that difference vector, i.e., the Euclidean norm
Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, that is, in Euclid's ''Elements'', it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are Euclidean ...
. This formula shows that if two quadric vectors ''X''1 and ''X''2 are orthogonal (perpendicular) to one another—that is, if (''X''1, ''X''2)=0—then their corresponding circles are tangent. For if the two signs ''s''1 and ''s''2 are the same (i.e. the circles have the same "orientation"), the circles are internally tangent; the distance between their centers equals the ''difference'' in the radii
:
Conversely, if the two signs ''s''1 and ''s''2 are different (i.e. the circles have opposite "orientations"), the circles are externally tangent; the distance between their centers equals the ''sum'' of the radii
:
Therefore, Apollonius' problem can be re-stated in Lie geometry as a problem of finding perpendicular vectors on the Lie quadric; specifically, the goal is to identify solution vectors ''X''sol that belong to the Lie quadric and are also orthogonal (perpendicular) to the vectors ''X''1, ''X''2 and ''X''3 corresponding to the given circles.
:
The advantage of this re-statement is that one can exploit theorems from linear algebra
Linear algebra is the branch of mathematics concerning linear equations such as:
:a_1x_1+\cdots +a_nx_n=b,
linear maps such as:
:(x_1, \ldots, x_n) \mapsto a_1x_1+\cdots +a_nx_n,
and their representations in vector spaces and through matrice ...
on the maximum number of linearly independent
In the theory of vector spaces, a set of vectors is said to be if there is a nontrivial linear combination of the vectors that equals the zero vector. If no such linear combination exists, then the vectors are said to be . These concepts are ...
, simultaneously perpendicular vectors. This gives another way to calculate the maximum number of solutions and extend the theorem to higher-dimensional spaces.
Inversive methods
inversive geometry
Inversive activities are processes which self internalise the action concerned. For example, a person who has an Inversive personality internalises his emotion
Emotions are mental states brought on by neurophysiological changes, variou ...
. The basic strategy of inversive methods is to transform a given Apollonius problem into another Apollonius problem that is simpler to solve; the solutions to the original problem are found from the solutions of the transformed problem by undoing the transformation. Candidate transformations must change one Apollonius problem into another; therefore, they must transform the given points, circles and lines to other points, circles and lines, and no other shapes. Circle inversion
A circle is a shape consisting of all points in a plane that are at a given distance from a given point, the centre. Equivalently, it is the curve traced out by a point that moves in a plane so that its distance from a given point is const ...
has this property and allows the center and radius of the inversion circle to be chosen judiciously. Other candidates include the Euclidean plane isometries; however, they do not simplify the problem, since they merely shift, rotate
Rotation, or spin, is the circular movement of an object around a '' central axis''. A two-dimensional rotating object has only one possible central axis and can rotate in either a clockwise or counterclockwise direction. A three-dimensional ...
, and mirror
A mirror or looking glass is an object that reflects an image. Light that bounces off a mirror will show an image of whatever is in front of it, when focused through the lens of the eye or a camera. Mirrors reverse the direction of the im ...
the original problem.
Inversion in a circle with center O and radius ''R'' consists of the following operation (Figure 5): every point P is mapped into a new point P' such that O, P, and P' are collinear, and the product of the distances of P and P' to the center O equal the radius ''R'' squared
:
Thus, if P lies outside the circle, then P' lies within, and vice versa. When P is the same as O, the inversion is said to send P to infinity. (In complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates Function (mathematics), functions of complex numbers. It is helpful in many branches of mathemati ...
, "infinity" is defined in terms of the Riemann sphere
In mathematics, the Riemann sphere, named after Bernhard Riemann, is a model of the extended complex plane: the complex plane plus one point at infinity. This extended plane represents the extended complex numbers, that is, the complex numbers ...
.) Inversion has the useful property that lines and circles are always transformed into lines and circles, and points are always transformed into points. Circles are generally transformed into other circles under inversion; however, if a circle passes through the center of the inversion circle, it is transformed into a straight line, and vice versa. Importantly, if a circle crosses the circle of inversion at right angles (intersects perpendicularly), it is left unchanged by the inversion; it is transformed into itself.
Circle inversions correspond to a subset of Möbius transformation
In geometry and complex analysis, a Möbius transformation of the complex plane is a rational function of the form
f(z) = \frac
of one complex variable ''z''; here the coefficients ''a'', ''b'', ''c'', ''d'' are complex numbers satisfying ''ad' ...
s on the Riemann sphere
In mathematics, the Riemann sphere, named after Bernhard Riemann, is a model of the extended complex plane: the complex plane plus one point at infinity. This extended plane represents the extended complex numbers, that is, the complex numbers ...
. The planar Apollonius problem can be transferred to the sphere by an inverse stereographic projection; hence, solutions of the planar Apollonius problem also pertain to its counterpart on the sphere. Other inversive solutions to the planar problem are possible besides the common ones described below.
Pairs of solutions by inversion
inversion
Inversion or inversions may refer to:
Arts
* , a French gay magazine (1924/1925)
* ''Inversion'' (artwork), a 2005 temporary sculpture in Houston, Texas
* Inversion (music), a term with various meanings in music theory and musical set theory
* ...
, by the following argument.
In general, any three distinct circles have a unique circle—the radical circle—that intersects all of them perpendicularly; the center of that circle is the radical center
The term radical center can refer to:
* Radical centrism, a political movement
* a mathematical construct: also called the power center (geometry)
In geometry, the power center of three circles, also called the radical center, is the interse ...
of the three circles. For illustration, the orange circle in Figure 6 crosses the black given circles at right angles. Inversion
Inversion or inversions may refer to:
Arts
* , a French gay magazine (1924/1925)
* ''Inversion'' (artwork), a 2005 temporary sculpture in Houston, Texas
* Inversion (music), a term with various meanings in music theory and musical set theory
* ...
in the radical circle leaves the given circles unchanged, but transforms the two conjugate pink solution circles into one another. Under the same inversion, the corresponding points of tangency of the two solution circles are transformed into one another; for illustration, in Figure 6, the two blue points lying on each green line are transformed into one another. Hence, the lines connecting these conjugate tangent points are invariant under the inversion; therefore, they must pass through the center of inversion, which is the radical center (green lines intersecting at the orange dot in Figure 6).
Inversion to an annulus
If two of the three given circles do not intersect, a center of inversion can be chosen so that those two given circles becomeconcentric
In geometry, two or more objects are said to be concentric, coaxal, or coaxial when they share the same center or axis. Circles, regular polygons and regular polyhedra, and spheres may be concentric to one another (sharing the same center p ...
. Under this inversion, the solution circles must fall within the annulus
Annulus (or anulus) or annular indicates a ring- or donut-shaped area or structure. It may refer to:
Human anatomy
* ''Anulus fibrosus disci intervertebralis'', spinal structure
* Annulus of Zinn, a.k.a. annular tendon or ''anulus tendineus com ...
between the two concentric circles. Therefore, they belong to two one-parameter families. In the first family (Figure 7), the solutions do ''not'' enclose the inner concentric circle, but rather revolve like ball bearings in the annulus. In the second family (Figure 8), the solution circles enclose the inner concentric circle. There are generally four solutions for each family, yielding eight possible solutions, consistent with the algebraic solution
A solution in radicals or algebraic solution is a closed-form expression, and more specifically a closed-form algebraic expression, that is the solution of a polynomial equation, and relies only on addition, subtraction, multiplication, divisi ...
.
Gauss
Johann Carl Friedrich Gauss (; german: Gauß ; la, Carolus Fridericus Gauss; 30 April 177723 February 1855) was a German mathematician and physicist who made significant contributions to many fields in mathematics and science. Sometimes refer ...
. The radii of the three given circles are known, as is the distance ''d''non from the common concentric center to the non-concentric circle (Figure 7). The solution circle can be determined from its radius ''r''s, the angle θ, and the distances ''d''s and ''d''T from its center to the common concentric center and the center of the non-concentric circle, respectively. The radius and distance ''d''s are known (Figure 7), and the distance ''d''T = ''r''s ± ''r''non, depending on whether the solution circle is internally or externally tangent to the non-concentric circle. Therefore, by the law of cosines
In trigonometry, the law of cosines (also known as the cosine formula, cosine rule, or al-Kashi's theorem) relates the lengths of the sides of a triangle to the cosine of one of its angles. Using notation as in Fig. 1, the law of cosines states ...
,
:
Here, a new constant ''C'' has been defined for brevity, with the subscript indicating whether the solution is externally or internally tangent. A simple trigonometric rearrangement yields the four solutions
:
This formula represents four solutions, corresponding to the two choices of the sign of θ, and the two choices for ''C''. The remaining four solutions can be obtained by the same method, using the substitutions for ''r''s and ''d''s indicated in Figure 8. Thus, all eight solutions of the general Apollonius problem can be found by this method.
Any initial two disjoint given circles can be rendered concentric as follows. The radical axis
In Euclidean geometry, the radical axis of two non-concentric circles is the set of points whose power with respect to the circles are equal. For this reason the radical axis is also called the power line or power bisector of the two circles. ...
of the two given circles is constructed; choosing two arbitrary points P and Q on this radical axis, two circles can be constructed that are centered on P and Q and that intersect the two given circles orthogonally. These two constructed circles intersect each other in two points. Inversion in one such intersection point F renders the constructed circles into straight lines emanating from F and the two given circles into concentric circles, with the third given circle becoming another circle (in general). This follows because the system of circles is equivalent to a set of Apollonian circles
In geometry, Apollonian circles are two families (pencils) of circles such that every circle in the first family intersects every circle in the second family orthogonally, and vice versa. These circles form the basis for bipolar coordinates. Th ...
, forming a bipolar coordinate system.
Resizing and inversion
The usefulness ofinversion
Inversion or inversions may refer to:
Arts
* , a French gay magazine (1924/1925)
* ''Inversion'' (artwork), a 2005 temporary sculpture in Houston, Texas
* Inversion (music), a term with various meanings in music theory and musical set theory
* ...
can be increased significantly by resizing. As noted in Viète's reconstruction, the three given circles and the solution circle can be resized in tandem while preserving their tangencies. Thus, the initial Apollonius problem is transformed into another problem that may be easier to solve. For example, the four circles can be resized so that one given circle is shrunk to a point; alternatively, two given circles can often be resized so that they are tangent to one another. Thirdly, given circles that intersect can be resized so that they become non-intersecting, after which the method for inverting to an annulus can be applied. In all such cases, the solution of the original Apollonius problem is obtained from the solution of the transformed problem by undoing the resizing and inversion.
= Shrinking one given circle to a point
= In the first approach, the given circles are shrunk or swelled (appropriately to their tangency) until one given circle is shrunk to a point P. In that case, Apollonius' problem degenerates to the CCP limiting case, which is the problem of finding a solution circle tangent to the two remaining given circles that passes through the point P. Inversion in a circle centered on P transforms the two given circles into new circles, and the solution circle into a line. Therefore, the transformed solution is a line that is tangent to the two transformed given circles. There are four such solution lines, which may be constructed from the external and internalhomothetic center
In geometry, a homothetic center (also called a center of similarity or a center of similitude) is a point from which at least two geometrically similar figures can be seen as a dilation or contraction of one another. If the center is ''externa ...
s of the two circles. Re-inversion in P and undoing the resizing transforms such a solution line into the desired solution circle of the original Apollonius problem. All eight general solutions can be obtained by shrinking and swelling the circles according to the differing internal and external tangencies of each solution; however, different given circles may be shrunk to a point for different solutions.
= Resizing two given circles to tangency
= In the second approach, the radii of the given circles are modified appropriately by an amount Δ''r'' so that two of them are tangential (touching). Their point of tangency is chosen as the center of inversion in a circle that intersects each of the two touching circles in two places. Upon inversion, the touching circles become two parallel lines: Their only point of intersection is sent to infinity under inversion, so they cannot meet. The same inversion transforms the third circle into another circle. The solution of the inverted problem must either be (1) a straight line parallel to the two given parallel lines and tangent to the transformed third given circle; or (2) a circle of constant radius that is tangent to the two given parallel lines and the transformed given circle. Re-inversion and adjusting the radii of all circles by Δ''r'' produces a solution circle tangent to the original three circles.Gergonne's solution
radical center
The term radical center can refer to:
* Radical centrism, a political movement
* a mathematical construct: also called the power center (geometry)
In geometry, the power center of three circles, also called the radical center, is the interse ...
G lies on all three lines (Figure 6).
To locate a second point on the lines ''L''1, ''L''2 and ''L''3, Gergonne noted a reciprocal relationship between those lines and the radical axis
In Euclidean geometry, the radical axis of two non-concentric circles is the set of points whose power with respect to the circles are equal. For this reason the radical axis is also called the power line or power bisector of the two circles. ...
''R'' of the solution circles, ''C''A and ''C''B. To understand this reciprocal relationship, consider the two tangent lines to the circle ''C''1 drawn at its tangent points A1 and B1 with the solution circles; the intersection of these tangent lines is the pole
Pole may refer to:
Astronomy
*Celestial pole, the projection of the planet Earth's axis of rotation onto the celestial sphere; also applies to the axis of rotation of other planets
*Pole star, a visible star that is approximately aligned with the ...
point of ''L''1 in ''C''1. Since the distances from that pole point to the tangent points A1 and B1 are equal, this pole point must also lie on the radical axis ''R'' of the solution circles, by definition (Figure 9). The relationship between pole points and their polar lines is reciprocal; if the pole of ''L''1 in ''C''1 lies on ''R'', the pole of ''R'' in ''C''1 must conversely lie on ''L''1. Thus, if we can construct ''R'', we can find its pole P1 in ''C''1, giving the needed second point on ''L''1 (Figure 10).
radical axis
In Euclidean geometry, the radical axis of two non-concentric circles is the set of points whose power with respect to the circles are equal. For this reason the radical axis is also called the power line or power bisector of the two circles. ...
of a potential pair of solution circles. To show this, Gergonne considered lines through corresponding points of tangency on two of the given circles, e.g., the line defined by A1/A2 and the line defined by B1/B2. Let X3 be a center of similitude for the two circles ''C''1 and ''C''2; then, A1/A2 and B1/B2 are pairs of antihomologous points, and their lines intersect at X3. It follows, therefore, that the products of distances are equal
:
which implies that X3 lies on the radical axis of the two solution circles. The same argument can be applied to the other pairs of circles, so that three centers of similitude for the given three circles must lie on the radical axes of pairs of solution circles.
In summary, the desired line ''L''1 is defined by two points: the radical center G of the three given circles and the pole in ''C''1 of one of the four lines connecting the homothetic centers. Finding the same pole in ''C''2 and ''C''3 gives ''L''2 and ''L''3, respectively; thus, all six points can be located, from which one pair of solution circles can be found. Repeating this procedure for the remaining three homothetic-center lines yields six more solutions, giving eight solutions in all. However, if a line ''L''''k'' does not intersect its circle ''C''''k'' for some ''k'', there is no pair of solutions for that homothetic-center line.
Intersection theory
The techniques of modernalgebraic geometry
Algebraic geometry is a branch of mathematics, classically studying zeros of multivariate polynomials. Modern algebraic geometry is based on the use of abstract algebraic techniques, mainly from commutative algebra, for solving geometrical ...
, and in particular intersection theory
In mathematics, intersection theory is one of the main branches of algebraic geometry, where it gives information about the intersection of two subvarieties of a given variety. The theory for varieties is older, with roots in Bézout's theorem o ...
, can be used to solve Apollonius's problem. In this approach, the problem is reinterpreted as a statement about circles in the complex projective plane
In mathematics, the complex projective plane, usually denoted P2(C), is the two-dimensional complex projective space. It is a complex manifold of complex dimension 2, described by three complex coordinates
:(Z_1,Z_2,Z_3) \in \mathbf^3,\qquad (Z_1, ...
. Solutions involving complex numbers are allowed and degenerate situations are counted with multiplicity. When this is done, there are always eight solutions to the problem.Eisenbud, David and Harris, Joe, ''3264 and All That: A Second Course in Algebraic Geometry''. Cambridge University Press, 2016. . pp. 66–68.
Every quadratic equation in , , and determines a unique conic, its vanishing locus. Conversely, every conic in the complex projective plane has an equation, and that equation is unique up to an overall scaling factor (because rescaling an equation does not change its vanishing locus). Therefore, the set of all conics may be parametrized by five-dimensional projective space , where the correspondence is
:
A ''circle'' in the complex projective plane is defined to be a conic that passes through the two points and , where denotes a square root of . The points and are called the ''circular points''. The projective variety
In algebraic geometry, a projective variety over an algebraically closed field ''k'' is a subset of some projective ''n''-space \mathbb^n over ''k'' that is the zero-locus of some finite family of homogeneous polynomials of ''n'' + 1 variables wi ...
of all circles is the subvariety of consisting of those points which correspond to conics passing through the circular points. Substituting the circular points into the equation for a generic conic yields the two equations
:
:
Taking the sum and difference of these equations shows that it is equivalent to impose the conditions
: and .
Therefore, the variety of all circles is a three-dimensional linear subspace of . After rescaling and completing the square
:
In elementary algebra, completing the square is a technique for converting a quadratic polynomial of the form
:ax^2 + bx + c
to the form
:a(x-h)^2 + k
for some values of ''h'' and ''k''.
In other words, completing the square places a perfe ...
, these equations also demonstrate that every conic passing through the circular points has an equation of the form
:
which is the homogenization of the usual equation of a circle in the affine plane. Therefore, studying circles in the above sense is nearly equivalent to studying circles in the conventional sense. The only difference is that the above sense permits degenerate circles which are the union of two lines. The non-degenerate circles are called ''smooth circles'', while the degenerate ones are called ''singular
Singular may refer to:
* Singular, the grammatical number that denotes a unit quantity, as opposed to the plural and other forms
* Singular homology
* SINGULAR, an open source Computer Algebra System (CAS)
* Singular or sounder, a group of boar ...
circles.'' There are two types of singular circles. One is the union of the line at infinity with another line in the projective plane (possibly the line at infinity again), and the other is union of two lines in the projective plane, one through each of the two circular points. These are the limits of smooth circles as the radius tends to and , respectively. In the latter case, no point on either of the two lines has real coordinates except for the origin .
Let be a fixed smooth circle. If is any other circle, then, by the definition of a circle, and intersect at the circular points and . Because and are conics, Bézout's theorem
Bézout's theorem is a statement in algebraic geometry concerning the number of common zeros of polynomials in indeterminates. In its original form the theorem states that ''in general'' the number of common zeros equals the product of the deg ...
implies and intersect in four points total, when those points are counted with the proper intersection multiplicity
In mathematics, and especially in algebraic geometry, the intersection number generalizes the intuitive notion of counting the number of times two curves intersect to higher dimensions, multiple (more than 2) curves, and accounting properly for ta ...
. That is, there are four points of intersection , , , and , but some of these points might collide. Appolonius' problem is concerned with the situation where , meaning that the intersection multiplicity at that point is ; if is also equal to a circular point, this should be interpreted as the intersection multiplicity being .
Let be the variety of circles tangent to . This variety is a quadric cone in the of all circles. To see this, consider the incidence correspondence
:
For a curve that is the vanishing locus of a single equation , the condition that the curve meets at with multiplicity means that the Taylor series
In mathematics, the Taylor series or Taylor expansion of a function is an infinite sum of terms that are expressed in terms of the function's derivatives at a single point. For most common functions, the function and the sum of its Taylor ser ...
expansion of vanishes to order at ; it is therefore linear conditions on the coefficients of . This shows that, for each , the fiber of over is a cut out by two linear equations in the space of circles. Consequently, is irreducible of dimension . Since it is possible to exhibit a circle that is tangent to at only a single point, a generic element of must be tangent at only a single point. Therefore, the projection sending to is a birational morphism. It follows that the image of , which is , is also irreducible and two dimensional.
To determine the shape of , fix two distinct circles and , not necessarily tangent to . These two circles determine a pencil
A pencil () is a writing or drawing implement with a solid pigment core in a protective casing that reduces the risk of core breakage, and keeps it from marking the user's hand.
Pencils create marks by physical abrasion, leaving a tra ...
, meaning a line in the of circles. If the equations of and are and , respectively, then the points on correspond to the circles whose equations are , where is a point of . The points where meets are precisely the circles in the pencil that are tangent to .
There are two possibilities for the number of points of intersections. One is that either or , say , is the equation for . In this case, is a line through . If is tangent to , then so is every circle in the pencil, and therefore is contained in . The other possibility is that neither nor is the equation for . In this case, the function is a quotient of quadratics, neither of which vanishes identically. Therefore, it vanishes at two points and has poles
Poles,, ; singular masculine: ''Polak'', singular feminine: ''Polka'' or Polish people, are a West Slavic nation and ethnic group, who share a common history, culture, the Polish language and are identified with the country of Poland in ...
at two points. These are the points in and , respectively, counted with multiplicity and with the circular points deducted. The rational function determines a morphism of degree two. The fiber over is the set of points for which . These are precisely the points at which the circle whose equation is meets . The branch point
In the mathematical field of complex analysis, a branch point of a multi-valued function (usually referred to as a "multifunction" in the context of complex analysis) is a point such that if the function is n-valued (has n values) at that point, ...
s of this morphism are the circles tangent to . By the Riemann–Hurwitz formula In mathematics, the Riemann–Hurwitz formula, named after Bernhard Riemann and Adolf Hurwitz, describes the relationship of the Euler characteristics of two surfaces when one is a ''ramified covering'' of the other. It therefore connects ramifi ...
, there are precisely two branch points, and therefore meets in two points. Together, these two possibilities for the intersection of and demonstrate that is a quadric cone. All such cones in are the same up to a change of coordinates, so this completely determines the shape of .
To conclude the argument, let , , and be three circles. If the intersection is finite, then it has degree , and therefore there are eight solutions to the problem of Apollonius, counted with multiplicity. To prove that the intersection is generically finite, consider the incidence correspondence
:
There is a morphism which projects onto its final factor of . The fiber over is . This has dimension , so has dimension . Because also has dimension , the generic fiber of the projection from to the first three factors cannot have positive dimension. This proves that generically, there are eight solutions counted with multiplicity. Since it is possible to exhibit a configuration where the eight solutions are distinct, the generic configuration must have all eight solutions distinct.
Radii
In the generic problem with eight solution circles, The reciprocals of the radii of four of the solution circles sum to the same value as do the reciprocals of the radii of the other four solution circlesSpecial cases
Ten combinations of points, circles, and lines
Apollonius problem is to construct one or more circles tangent to three given objects in a plane, which may be circles, points, or lines. This gives rise to ten types of Apollonius' problem, one corresponding to each combination of circles, lines and points, which may be labeled with three letters, either C, L, or P, to denote whether the given elements are a circle, line or point, respectively (Table 1
Table may refer to:
* Table (furniture), a piece of furniture with a flat surface and one or more legs
* Table (landform), a flat area of land
* Table (information), a data arrangement with rows and columns
* Table (database), how the table data ...
). As an example, the type of Apollonius problem with a given circle, line, and point is denoted as CLP.
Some of these special case
In logic, especially as applied in mathematics, concept is a special case or specialization of concept precisely if every instance of is also an instance of but not vice versa, or equivalently, if is a generalization of . A limiting case ...
s are much easier to solve than the general case of three given circles. The two simplest cases are the problems of drawing a circle through three given points (PPP) or tangent to three lines (LLL), which were solved first by Euclid
Euclid (; grc-gre, Εὐκλείδης; BC) was an ancient Greek mathematician active as a geometer and logician. Considered the "father of geometry", he is chiefly known for the '' Elements'' treatise, which established the foundations of ...
in his '' Elements''. For example, the PPP problem can be solved as follows. The center of the solution circle is equally distant from all three points, and therefore must lie on the perpendicular bisector
In geometry, bisection is the division of something into two equal or congruent parts, usually by a line, which is then called a ''bisector''. The most often considered types of bisectors are the ''segment bisector'' (a line that passes through ...
line of any two. Hence, the center is the point of intersection of any two perpendicular bisectors. Similarly, in the LLL case, the center must lie on a line bisecting the angle at the three intersection points between the three given lines; hence, the center lies at the intersection point of two such angle bisectors. Since there are two such bisectors at every intersection point of the three given lines, there are four solutions to the general LLL problem.
Points and lines may be viewed as special cases of circles; a point can be considered as a circle of infinitely small radius, and a line may be thought of an infinitely large circle whose center is also at infinity. From this perspective, the general Apollonius problem is that of constructing circles tangent to three given circles. The nine other cases involving points and lines may be viewed as limiting cases of the general problem.These limiting cases often have fewer solutions than the general problem; for example, the replacement of a given circle by a given point halves the number of solutions, since a point can be construed as an infinitesimal circle that is either internally or externally tangent.
Number of solutions
enumerative geometry
In mathematics, enumerative geometry is the branch of algebraic geometry concerned with counting numbers of solutions to geometric questions, mainly by means of intersection theory.
History
The problem of Apollonius is one of the earliest examp ...
. The general number of solutions for each of the ten types of Apollonius' problem is given in Table 1 above. However, special arrangements of the given elements may change the number of solutions. For illustration, Apollonius' problem has no solution if one circle separates the two (Figure 11); to touch both the solid given circles, the solution circle would have to cross the dashed given circle; but that it cannot do, if it is to touch the dashed circle tangentially. Conversely, if three given circles are all tangent at the same point, then ''any'' circle tangent at the same point is a solution; such Apollonius problems have an infinite number of solutions. If any of the given circles are identical, there is likewise an infinity of solutions. If only two given circles are identical, there are only two distinct given circles; the centers of the solution circles form a hyperbola
In mathematics, a hyperbola (; pl. hyperbolas or hyperbolae ; adj. hyperbolic ) is a type of smooth curve lying in a plane, defined by its geometric properties or by equations for which it is the solution set. A hyperbola has two pieces, ca ...
, as used in one solution to Apollonius' problem.
An exhaustive enumeration of the number of solutions for all possible configurations of three given circles, points or lines was first undertaken by Muirhead in 1896, although earlier work had been done by Stoll and Study. However, Muirhead's work was incomplete; it was extended in 1974 and a definitive enumeration, with 33 distinct cases, was published in 1983. Although solutions to Apollonius' problem generally occur in pairs related by inversion
Inversion or inversions may refer to:
Arts
* , a French gay magazine (1924/1925)
* ''Inversion'' (artwork), a 2005 temporary sculpture in Houston, Texas
* Inversion (music), a term with various meanings in music theory and musical set theory
* ...
, an odd number of solutions is possible in some cases, e.g., the single solution for PPP, or when one or three of the given circles are themselves solutions. (An example of the latter is given in the section
Section, Sectioning or Sectioned may refer to:
Arts, entertainment and media
* Section (music), a complete, but not independent, musical idea
* Section (typography), a subdivision, especially of a chapter, in books and documents
** Section sig ...
on Descartes' theorem.) However, there are no Apollonius problems with seven solutions. Alternative solutions based on the geometry of circles and spheres have been developed and used in higher dimensions.
Mutually tangent given circles: Soddy's circles and Descartes' theorem
If the three given circles are mutually tangent, Apollonius' problem has five solutions. Three solutions are the given circles themselves, since each is tangent to itself and to the other two given circles. The remaining two solutions (shown in red in Figure 12) correspond to theinscribed
{{unreferenced, date=August 2012
An inscribed triangle of a circle
In geometry, an inscribed planar shape or solid is one that is enclosed by and "fits snugly" inside another geometric shape or solid. To say that "figure F is inscribed in figu ...
and circumscribed circle
In geometry, the circumscribed circle or circumcircle of a polygon is a circle that passes through all the vertices of the polygon. The center of this circle is called the circumcenter and its radius is called the circumradius.
Not every polyg ...
s, and are called ''Soddy's circles''. This special case of Apollonius' problem is also known as the four coins problem. The three given circles of this Apollonius problem form a Steiner chain
In geometry, a Steiner chain is a set of circles, all of which are tangent to two given non-intersecting circles (blue and red in Figure 1), where is finite and each circle in the chain is tangent to the previous and next circles in the chain. ...
tangent to the two Soddy's circles.
Elizabeth of Bohemia
Elizabeth Stuart (19 August 159613 February 1662) was Electress of the Palatinate and briefly Queen of Bohemia as the wife of Frederick V of the Palatinate. Since her husband's reign in Bohemia lasted for just one winter, she is called the Wi ...
, René Descartes
René Descartes ( or ; ; Latinized: Renatus Cartesius; 31 March 1596 – 11 February 1650) was a French philosopher, scientist, and mathematician, widely considered a seminal figure in the emergence of modern philosophy and science. Ma ...
showed that
:
where ''k''''s'' = 1/''r''''s'' and ''r''''s'' are the curvature
In mathematics, curvature is any of several strongly related concepts in geometry. Intuitively, the curvature is the amount by which a curve deviates from being a straight line, or a surface deviates from being a plane.
For curves, the can ...
and radius of the solution circle, respectively, and similarly for the curvatures ''k''1, ''k''2 and ''k''3 and radii ''r''1, ''r''2 and ''r''3 of the three given circles. For every set of four mutually tangent circles, there is a second set of four mutually tangent circles that are tangent at the same six points.
Descartes' theorem was rediscovered independently in 1826 by Jakob Steiner
Jakob Steiner (18 March 1796 – 1 April 1863) was a Swiss mathematician who worked primarily in geometry.
Life
Steiner was born in the village of Utzenstorf, Canton of Bern. At 18, he became a pupil of Heinrich Pestalozzi and afterwards st ...
, in 1842 by Philip Beecroft,MathWords online article
) and again in 1936 by
Frederick Soddy
Frederick Soddy FRS (2 September 1877 – 22 September 1956) was an English radiochemist who explained, with Ernest Rutherford, that radioactivity is due to the transmutation of elements, now known to involve nuclear reactions. He also prov ...
. Soddy published his findings in the scientific journal ''Nature
Nature, in the broadest sense, is the physical world or universe. "Nature" can refer to the phenomena of the physical world, and also to life in general. The study of nature is a large, if not the only, part of science. Although humans are ...
'' as a poem, ''The Kiss Precise'', of which the first two stanzas are reproduced below. The first stanza describes Soddy's circles, whereas the second stanza gives Descartes' theorem. In Soddy's poem, two circles are said to "kiss" if they are tangent, whereas the term "bend" refers to the curvature ''k'' of the circle.
:: ''For pairs of lips to kiss maybe''
:: ''Involves no trigonometry.''
:: Tis not so when four circles kiss''
:: ''Each one the other three.''
:: ''To bring this off the four must be''
:: ''As three in one or one in three.''
:: ''If one in three, beyond a doubt''
:: ''Each gets three kisses from without.''
:: ''If three in one, then is that one''
:: ''Thrice kissed internally.''
: ''Four circles to the kissing come.''
: ''The smaller are the benter.''
: ''The bend is just the inverse of''
: ''The distance from the center.''
: ''Though their intrigue left Euclid dumb''
: ''There's now no need for rule of thumb.''
: ''Since zero bend's a dead straight line''
: ''And concave bends have minus sign,''
: ''The sum of the squares of all four bends''
: ''Is half the square of their sum.''
Sundry extensions of Descartes' theorem have been derived by Daniel Pedoe.
Generalizations
Apollonius' problem can be extended to construct all the circles that intersect three given circles at a precise angle θ, or at three specified crossing angles θ1, θ2 and θ3; the ordinary Apollonius' problem corresponds to a special case in which the crossing angle is zero for all three given circles. Another generalization is the dual of the first extension, namely, to construct circles with three specified tangential distances from the three given circles.sphere
A sphere () is a geometrical object that is a three-dimensional analogue to a two-dimensional circle. A sphere is the set of points that are all at the same distance from a given point in three-dimensional space.. That given point is the c ...
and other quadratic surfaces. For the sphere, the problem is to construct all the circles (the boundaries of spherical cap
In geometry, a spherical cap or spherical dome is a portion of a sphere or of a ball cut off by a plane. It is also a spherical segment of one base, i.e., bounded by a single plane. If the plane passes through the center of the sphere (formin ...
s) that are tangent to three given circles on the sphere. This spherical problem can be rendered into a corresponding planar problem using stereographic projection
In mathematics, a stereographic projection is a perspective projection of the sphere, through a specific point on the sphere (the ''pole'' or ''center of projection''), onto a plane (the ''projection plane'') perpendicular to the diameter thro ...
. Once the solutions to the planar problem have been constructed, the corresponding solutions to the spherical problem can be determined by inverting the stereographic projection. Even more generally, one can consider the problem of four tangent curves that result from the intersections of an arbitrary quadratic surface and four planes, a problem first considered by Charles Dupin
Baron Pierre Charles François Dupin (6 October 1784, Varzy, Nièvre – 18 January 1873, Paris, France) was a French Catholic mathematician, engineer, economist and politician, particularly known for work in the field of mathematics, where the ...
.
By solving Apollonius' problem repeatedly to find the inscribed circle, the interstices between mutually tangential circles can be filled arbitrarily finely, forming an Apollonian gasket
In mathematics, an Apollonian gasket or Apollonian net is a fractal generated by starting with a triple of circles, each tangent to the other two, and successively filling in more circles, each tangent to another three. It is named after Greek ...
, also known as a ''Leibniz packing'' or an ''Apollonian packing''. This gasket is a fractal
In mathematics, a fractal is a geometric shape containing detailed structure at arbitrarily small scales, usually having a fractal dimension strictly exceeding the topological dimension. Many fractals appear similar at various scales, as ill ...
, being self-similar and having a dimension
In physics and mathematics, the dimension of a mathematical space (or object) is informally defined as the minimum number of coordinates needed to specify any point within it. Thus, a line has a dimension of one (1D) because only one coord ...
''d'' that is not known exactly but is roughly 1.3,which is higher than that of a regular (or rectifiable) curve (''d'' = 1) but less than that of a plane (''d'' = 2). The Apollonian gasket was first described by
Gottfried Leibniz
Gottfried Wilhelm (von) Leibniz . ( – 14 November 1716) was a German polymath active as a mathematician, philosopher, scientist and diplomat. He is one of the most prominent figures in both the history of philosophy and the history of mathem ...
in the 17th century, and is a curved precursor of the 20th-century Sierpiński triangle. The Apollonian gasket also has deep connections to other fields of mathematics; for example, it is the limit set of Kleinian group
In mathematics, a Kleinian group is a discrete subgroup of the group of orientation-preserving isometries of hyperbolic 3-space . The latter, identifiable with , is the quotient group of the 2 by 2 complex matrices of determinant 1 by their ...
s.
The configuration of a circle tangent to ''four'' circles in the plane has special properties, which have been elucidated by Larmor (1891) and Lachlan (1893). Such a configuration is also the basis for Casey's theorem, itself a generalization of Ptolemy's theorem
In Euclidean geometry, Ptolemy's theorem is a relation between the four sides and two diagonals of a cyclic quadrilateral (a quadrilateral whose vertices lie on a common circle). The theorem is named after the Greek astronomer and mathematici ...
.
The extension of Apollonius' problem to three dimensions, namely, the problem of finding a fifth sphere that is tangent to four given spheres, can be solved by analogous methods. For example, the given and solution spheres can be resized so that one given sphere is shrunk to point while maintaining tangency. Inversion in this point reduces Apollonius' problem to finding a plane that is tangent to three given spheres. There are in general eight such planes, which become the solutions to the original problem by reversing the inversion and the resizing. This problem was first considered by Pierre de Fermat
Pierre de Fermat (; between 31 October and 6 December 1607 – 12 January 1665) was a French mathematician who is given credit for early developments that led to infinitesimal calculus, including his technique of adequality. In particular, he ...
, and many alternative solution methods have been developed over the centuries. Reprinted in Euler's ''Opera Omnia'', series 1, volume 26, pp. 334–343.Apollonius' problem can even be extended to ''d'' dimensions, to construct the
hypersphere
In mathematics, an -sphere or a hypersphere is a topological space that is homeomorphic to a ''standard'' -''sphere'', which is the set of points in -dimensional Euclidean space that are situated at a constant distance from a fixed point, call ...
s tangent to a given set of hyperspheres. Following the publication of Frederick Soddy
Frederick Soddy FRS (2 September 1877 – 22 September 1956) was an English radiochemist who explained, with Ernest Rutherford, that radioactivity is due to the transmutation of elements, now known to involve nuclear reactions. He also prov ...
's re-derivation of the Descartes theorem in 1936, several people solved (independently) the mutually tangent case corresponding to Soddy's circles in ''d'' dimensions.
Applications
The principal application of Apollonius' problem, as formulated by Isaac Newton, is hyperbolic trilateration, which seeks to determine a position from the ''differences'' in distances to at least three points. For example, a ship may seek to determine its position from the differences in arrival times of signals from three synchronized transmitters. Solutions to Apollonius' problem were used inWorld War I
World War I (28 July 1914 11 November 1918), often abbreviated as WWI, was List of wars and anthropogenic disasters by death toll, one of the deadliest global conflicts in history. Belligerents included much of Europe, the Russian Empire, ...
to determine the location of an artillery piece from the time a gunshot was heard at three different positions, and hyperbolic trilateration is the principle used by the Decca Navigator System
The Decca Navigator System was a hyperbolic radio navigation system which allowed ships and aircraft to determine their position by using radio signals from a dedicated system of static radio transmitters. The system used phase comparison of t ...
and LORAN
LORAN, short for long range navigation, was a hyperbolic radio navigation system developed in the United States during World War II. It was similar to the UK's Gee system but operated at lower frequencies in order to provide an improved range ...
. Similarly, the location of an aircraft may be determined from the difference in arrival times of its transponder
In telecommunications, a transponder is a device that, upon receiving a signal, emits a different signal in response. The term is a blend of ''transmitter'' and ''responder''.
In air navigation or radio frequency identification, a flight trans ...
signal at four receiving stations. This multilateration Trilateration is the use of distances (or "ranges") for determining the unknown position coordinates of a point of interest, often around Earth (geopositioning).
When more than three distances are involved, it may be called multilateration, for e ...
problem is equivalent to the three-dimensional generalization of Apollonius' problem and applies to global navigation satellite systems
A satellite navigation or satnav system is a system that uses satellites to provide autonomous geo-spatial positioning. It allows satellite navigation devices to determine their location (longitude, latitude, and altitude/elevation) to high pr ...
(see GPS#Geometric interpretation). It is also used to determine the position of calling animals (such as birds and whales), although Apollonius' problem does not pertain if the speed of sound
The speed of sound is the distance travelled per unit of time by a sound wave as it propagates through an elastic medium. At , the speed of sound in air is about , or one kilometre in or one mile in . It depends strongly on temperature as we ...
varies with direction (i.e., the transmission medium
A transmission medium is a system or substance that can mediate the propagation of signals for the purposes of telecommunication. Signals are typically imposed on a wave of some kind suitable for the chosen medium. For example, data can modulat ...
not isotropic
Isotropy is uniformity in all orientations; it is derived . Precise definitions depend on the subject area. Exceptions, or inequalities, are frequently indicated by the prefix ' or ', hence '' anisotropy''. ''Anisotropy'' is also used to describ ...
).
Apollonius' problem has other applications. In Book 1, Proposition 21 in his '' Principia'', Isaac Newton
Sir Isaac Newton (25 December 1642 – 20 March 1726/27) was an English mathematician, physicist, astronomer, alchemist, Theology, theologian, and author (described in his time as a "natural philosophy, natural philosopher"), widely ...
used his solution of Apollonius' problem to construct an orbit in celestial mechanics
Celestial mechanics is the branch of astronomy that deals with the motions of objects in outer space. Historically, celestial mechanics applies principles of physics (classical mechanics) to astronomical objects, such as stars and planets, ...
from the center of attraction and observations of tangent lines to the orbit corresponding to instantaneous velocity
Velocity is the directional speed of an object in motion as an indication of its rate of change in position as observed from a particular frame of reference and as measured by a particular standard of time (e.g. northbound). Velocity i ...
. The special case of the problem of Apollonius when all three circles are tangent is used in the Hardy–Littlewood circle method of analytic number theory
In mathematics, analytic number theory is a branch of number theory that uses methods from mathematical analysis to solve problems about the integers. It is often said to have begun with Peter Gustav Lejeune Dirichlet's 1837 introduction of Diri ...
to construct Hans Rademacher
Hans Adolph Rademacher (; 3 April 1892, Wandsbeck, now Hamburg-Wandsbek – 7 February 1969, Haverford, Pennsylvania, USA) was a German-born American mathematician, known for work in mathematical analysis and number theory.
Biography
Rademacher r ...
's contour for complex integration, given by the boundaries of an infinite set
In set theory, an infinite set is a set that is not a finite set. Infinite sets may be countable or uncountable.
Properties
The set of natural numbers (whose existence is postulated by the axiom of infinity) is infinite. It is the only s ...
of Ford circles each of which touches several others. Finally, Apollonius' problem has been applied to some types of packing problem
Packing problems are a class of optimization problems in mathematics that involve attempting to pack objects together into containers. The goal is to either pack a single container as densely as possible or pack all objects using as few conta ...
s, which arise in disparate fields such as the error-correcting code
In computing, telecommunication, information theory, and coding theory, an error correction code, sometimes error correcting code, (ECC) is used for controlling errors in data over unreliable or noisy communication channels. The central idea i ...
s used on DVDs and the design of pharmaceuticals that bind in a particular enzyme
Enzymes () are proteins that act as biological catalysts by accelerating chemical reactions. The molecules upon which enzymes may act are called substrates, and the enzyme converts the substrates into different molecules known as products ...
of a pathogenic bacterium
Bacteria (; singular: bacterium) are ubiquitous, mostly free-living organisms often consisting of one biological cell. They constitute a large domain of prokaryotic microorganisms. Typically a few micrometres in length, bacteria were am ...
.
See also
* Apollonius point *Apollonius' theorem
In geometry, Apollonius's theorem is a theorem relating the length of a median of a triangle to the lengths of its sides.
It states that "the sum of the squares of any two sides of any triangle equals twice the square on half the third side ...
* Isodynamic point
In Euclidean geometry, the isodynamic points of a triangle are points associated with the triangle, with the properties that an inversion centered at one of these points transforms the given triangle into an equilateral triangle, and that the dis ...
of a triangle
References
Further reading
* * * * * Trans., introd., and notes by Paul Ver Eecke. * *External links
* * * * * {{DEFAULTSORT:Problem Of Apollonius Conformal geometry Euclidean plane geometry Incidence geometry History of geometry