
Newton's laws of motion are three basic
law
Law is a set of rules that are created and are enforceable by social or governmental institutions to regulate behavior,Robertson, ''Crimes against humanity'', 90. with its precise definition a matter of longstanding debate. It has been vario ...
s of
classical mechanics
Classical mechanics is a physical theory describing the motion of macroscopic objects, from projectiles to parts of machinery, and astronomical objects, such as spacecraft, planets, stars, and galaxies. For objects governed by classi ...
that describe the relationship between the
motion of an object and the
forces acting on it. These laws can be paraphrased as follows:
# A body remains at rest, or in motion at a constant speed in a straight line, unless acted upon by a force.
# When a body is acted upon by a force, the time rate of change of its
momentum equals the force.
# If two bodies exert forces on each other, these forces have the same magnitude but opposite directions.
The three laws of motion were first stated by
Isaac Newton in his ''
Philosophiæ Naturalis Principia Mathematica'' (''Mathematical Principles of Natural Philosophy''), originally published in 1687. Newton used them to investigate and explain the motion of many physical objects and systems, which laid the foundation for classical mechanics. In the time since Newton, the conceptual content of classical physics has been reformulated in alternative ways, involving different mathematical approaches that have yielded insights which were obscured in the original, Newtonian formulation. Limitations to Newton's laws have also been discovered; new theories are necessary when objects move at very high speeds (
special relativity), are very massive (
general relativity
General relativity, also known as the general theory of relativity and Einstein's theory of gravity, is the geometric theory of gravitation published by Albert Einstein in 1915 and is the current description of gravitation in modern physics ...
), or are very small (
quantum mechanics
Quantum mechanics is a fundamental theory in physics that provides a description of the physical properties of nature at the scale of atoms and subatomic particles. It is the foundation of all quantum physics including quantum chemistr ...
).
Prerequisites
Newton's laws are often stated in terms of ''point'' or ''particle'' masses, that is, bodies whose volume is negligible. This is a reasonable approximation for real bodies when the motion of internal parts can be neglected, and when the separation between bodies is much larger than the size of each. For instance, the Earth and the Sun can both be approximated as pointlike when considering the orbit of the former around the latter, but the Earth is not pointlike when considering activities on its surface.
The mathematical description of motion, or
kinematics, is based on the idea of specifying positions using numerical coordinates. Movement is represented by these numbers changing over time: a body's trajectory is represented by a function that assigns to each value of a time variable the values of all the position coordinates. The simplest case is one-dimensional, that is, when a body is constrained to move only along a straight line. Its position can then be given by a single number, indicating where it is relative to some chosen reference point. For example, a body might be free to slide along a track that runs left to right, and so its location can be specified by its distance from a convenient zero point, or
origin, with negative numbers indicating positions to the left and positive numbers indicating positions to the right. If the body's location as a function of time is
, then its average velocity over the time interval from
to
is
Here, the Greek letter
(
delta) is used, per tradition, to mean "change in". A positive average velocity means that the position coordinate
increases over the interval in question, a negative average velocity indicates a net decrease over that interval, and an average velocity of zero means that the body ends the time interval in the same place as it began.
Calculus
Calculus, originally called infinitesimal calculus or "the calculus of infinitesimals", is the mathematical study of continuous change, in the same way that geometry is the study of shape, and algebra is the study of generalizations of arithm ...
gives the means to define an ''instantaneous'' velocity, a measure of a body's speed and direction of movement at a single moment of time, rather than over an interval. One notation for the instantaneous velocity is to replace
with the symbol
, for example,
This denotes that the instantaneous velocity is the
derivative
In mathematics, the derivative of a function of a real variable measures the sensitivity to change of the function value (output value) with respect to a change in its argument (input value). Derivatives are a fundamental tool of calculus. ...
of the position with respect to time. It can roughly be thought of as the ratio between an infinitesimally small change in position
to the infinitesimally small time interval
over which it occurs.
More carefully, the velocity and all other derivatives can be defined using the concept of a
limit.
A function
has a limit of
at a given input value
if the difference between
and
can be made arbitrarily small by choosing an input sufficiently close to
. One writes,
Instantaneous velocity can be defined as the limit of the average velocity as the time interval shrinks to zero:
''Acceleration'' is to velocity as velocity is to position: it is the derivative of the velocity with respect to time. Acceleration can likewise be defined as a limit:
Consequently, the acceleration is the ''second derivative'' of position,
often written
.
Position, when thought of as a displacement from an origin point, is a
vector
Vector most often refers to:
*Euclidean vector, a quantity with a magnitude and a direction
*Vector (epidemiology), an agent that carries and transmits an infectious pathogen into another living organism
Vector may also refer to:
Mathematic ...
: a quantity with both magnitude and direction.
Velocity and acceleration are vector quantities as well. The mathematical tools of vector algebra provide the means to describe motion in two, three or more dimensions. Vectors are often denoted with an arrow, as in
, or in bold typeface, such as
. Often, vectors are represented visually as arrows, with the direction of the vector being the direction of the arrow, and the magnitude of the vector indicated by the length of the arrow. Numerically, a vector can be represented as a list; for example, a body's velocity vector might be
, indicating that it is moving at 3 metres per second along a horizontal axis and 4 metres per second along the vertical axis. The same motion described in a different
coordinate system will be represented by different numbers, and vector algebra can be used to translate between these alternatives.
The physics concept of ''force'' makes quantitative the everyday idea of a push or a pull. Forces in Newtonian mechanics are often due to strings and ropes, friction, muscle effort, gravity, and so forth. Like displacement, velocity, and acceleration, force is a vector quantity.
Laws
First

Translated from the Latin, Newton's first law reads,
:''Every body continues in its state of rest, or of uniform motion in a straight line, unless it is compelled to change that state by forces impressed upon it.''
Newton's first law expresses the principle of
inertia
Inertia is the idea that an object will continue its current motion until some force causes its speed or direction to change. The term is properly understood as shorthand for "the principle of inertia" as described by Newton in his first law ...
: the natural behavior of a body is to move in a straight line at constant speed. In the absence of outside influences, a body's motion preserves the status quo.
The modern understanding of Newton's first law is that no
inertial observer
In classical physics and special relativity, an inertial frame of reference (also called inertial reference frame, inertial frame, inertial space, or Galilean reference frame) is a frame of reference that is not undergoing any acceleratio ...
is privileged over any other. The concept of an inertial observer makes quantitative the everyday idea of feeling no effects of motion. For example, a person standing on the ground watching a train go past is an inertial observer. If the observer on the ground sees the train moving smoothly in a straight line at a constant speed, then a passenger sitting on the train will also be an inertial observer: the train passenger ''feels'' no motion. The principle expressed by Newton's first law is that there is no way to say which inertial observer is "really" moving and which is "really" standing still. One observer's state of rest is another observer's state of uniform motion in a straight line, and no experiment can deem either point of view to be correct or incorrect. There is no absolute standard of rest.
Second
:''The change of motion of an object is proportional to the force impressed; and is made in the direction of the straight line in which the force is impressed.''
By "motion", Newton meant the quantity now called
momentum, which depends upon the amount of matter contained in a body, the speed at which that body is moving, and the direction in which it is moving. In modern notation, the momentum of a body is the product of its mass and its velocity:
Newton's second law, in modern form, states that the time derivative of the momentum is the force:
If the mass
does not change with time, then the derivative acts only upon the velocity, and so the force equals the product of the mass and the time derivative of the velocity, which is the acceleration:
As the acceleration is the second derivative of position with respect to time, this can also be written

The forces acting on a body
add as vectors, and so the total force on a body depends upon both the magnitudes and the directions of the individual forces. When the net force on a body is equal to zero, then by Newton's second law, the body does not accelerate, and it is said to be in
mechanical equilibrium
In classical mechanics, a particle is in mechanical equilibrium if the net force on that particle is zero. By extension, a physical system made up of many parts is in mechanical equilibrium if the net force on each of its individual parts is zero ...
. A state of mechanical equilibrium is ''stable'' if, when the position of the body is changed slightly, the body remains near that equilibrium. Otherwise, the equilibrium is ''unstable.''
A common visual representation of forces acting in concert is the
free body diagram
A free body diagram consists of a diagrammatic representation of a single body or a subsystem of bodies isolated from its surroundings showing all the forces acting on it.
In physics and engineering, a free body diagram (FBD; also called a force ...
, which schematically portrays a body of interest and the forces applied to it by outside influences. For example, a free body diagram of a block sitting upon an
inclined plane can illustrate the combination of gravitational force,
"normal" force, friction, and string tension.
Newton's second law is sometimes presented as a ''definition'' of force, i.e., a force is that which exists when an inertial observer sees a body accelerating. In order for this to be more than a
tautology — acceleration implies force, force implies acceleration — some other statement about force must also be made. For example, an equation detailing the force might be specified, like
Newton's law of universal gravitation
Newton's law of universal gravitation is usually stated as that every particle attracts every other particle in the universe with a force that is proportional to the product of their masses and inversely proportional to the square of the distan ...
. By inserting such an expression for
into Newton's second law, an equation with predictive power can be written. Newton's second law has also been regarded as setting out a research program for physics, establishing that important goals of the subject are to identify the forces present in nature and to catalogue the constituents of matter.
Third
:''To every action, there is always opposed an equal reaction; or, the mutual actions of two bodies upon each other are always equal, and directed to contrary parts.''

Overly brief paraphrases of the third law, like "action equals
reaction
Reaction may refer to a process or to a response to an action, event, or exposure:
Physics and chemistry
*Chemical reaction
*Nuclear reaction
* Reaction (physics), as defined by Newton's third law
*Chain reaction (disambiguation).
Biology and m ...
" might have caused confusion among generations of students: the "action" and "reaction" apply to different bodies. For example, consider a book at rest on a table. The Earth's gravity pulls down upon the book. The "reaction" to that "action" is ''not'' the support force from the table holding up the book, but the gravitational pull of the book acting on the Earth.
Newton's third law relates to a more fundamental principle, the
conservation of momentum
In Newtonian mechanics, momentum (more specifically linear momentum or translational momentum) is the product of the mass and velocity of an object. It is a vector quantity, possessing a magnitude and a direction. If is an object's mass an ...
. The latter remains true even in cases where Newton's statement does not, for instance when
force fields as well as material bodies carry momentum, and when momentum is defined properly, in
quantum mechanics
Quantum mechanics is a fundamental theory in physics that provides a description of the physical properties of nature at the scale of atoms and subatomic particles. It is the foundation of all quantum physics including quantum chemistr ...
as well. In Newtonian mechanics, if two bodies have momenta
and
respectively, then the total momentum of the pair is
, and the rate of change of
is
By Newton's second law, the first term is the total force upon the first body, and the second term is the total force upon the second body. If the two bodies are isolated from outside influences, the only force upon the first body can be that from the second, and vice versa. By Newton's third law, these forces have equal magnitude but opposite direction, so they cancel when added, and
is constant. Alternatively, if
is known to be constant, it follows that the forces have equal magnitude and opposite direction.
Candidates for additional laws
Various sources have proposed elevating other ideas used in classical mechanics to the status of Newton's laws. For example, in Newtonian mechanics, the total mass of a body made by bringing together two smaller bodies is the sum of their individual masses.
Frank Wilczek
Frank Anthony Wilczek (; born May 15, 1951) is an American theoretical physicist, mathematician and Nobel laureate. He is currently the Herman Feshbach Professor of Physics at the Massachusetts Institute of Technology (MIT), Founding Direc ...
has suggested calling attention to this assumption by designating it "Newton's Zeroth Law". Another candidate for a "zeroth law" is the fact that at any instant, a body reacts to the forces applied to it at that instant. Likewise, the idea that forces add like vectors (or in other words obey the
superposition principle), and the idea that forces change the energy of a body, have both been described as a "fourth law".
Work and energy
Physicists developed the concept of
energy after Newton's time, but it has become an inseparable part of what is considered "Newtonian" physics. Energy can broadly be classified into
kinetic, due to a body's motion, and
potential
Potential generally refers to a currently unrealized ability. The term is used in a wide variety of fields, from physics to the social sciences to indicate things that are in a state where they are able to change in ways ranging from the simple r ...
, due to a body's position relative to others.
Thermal energy
The term "thermal energy" is used loosely in various contexts in physics and engineering. It can refer to several different well-defined physical concepts. These include the internal energy or enthalpy of a body of matter and radiation; heat, de ...
, the energy carried by heat flow, is a type of kinetic energy not associated with the macroscopic motion of objects but instead with the movements of the atoms and molecules of which they are made. According to the
work-energy theorem, when a force acts upon a body while that body moves along the line of the force, the force does ''work'' upon the body, and the amount of work done is equal to the change in the body's kinetic energy. In many cases of interest, the net work done by a force when a body moves in a closed loop — starting at a point, moving along some trajectory, and returning to the initial point — is zero. If this is the case, then the force can be written in terms of the
gradient of a function called a
scalar potential
In mathematical physics, scalar potential, simply stated, describes the situation where the difference in the potential energies of an object in two different positions depends only on the positions, not upon the path taken by the object in trav ...
:
This is true for many forces including that of gravity, but not for friction; indeed, almost any problem in a mechanics textbook that does not involve friction can be expressed in this way.
The fact that the force can be written in this way can be understood from the
conservation of energy. Without friction to dissipate a body's energy into heat, the body's energy will trade between potential and (non-thermal) kinetic forms while the total amount remains constant. Any gain of kinetic energy, which occurs when the net force on the body accelerates it to a higher speed, must be accompanied by a loss of potential energy. So, the net force upon the body is determined by the manner in which the potential energy decreases.
Examples
Uniformly accelerated motion
If a body falls from rest near the surface of the Earth, then in the absence of air resistance, it will accelerate at a constant rate. This is known as
free fall
In Newtonian physics, free fall is any motion of a body where gravity is the only force acting upon it. In the context of general relativity, where gravitation is reduced to a space-time curvature, a body in free fall has no force acting on ...
. The speed attained during free fall is proportional to the elapsed time, and the distance traveled is proportional to the square of the elapsed time. Importantly, the acceleration is the same for all bodies, independently of their mass. This follows from combining Newton's second law of motion with his
law of universal gravitation. The latter states that the magnitude of the gravitational force from the Earth upon the body is
where
is the mass of the falling body,
is the mass of the Earth,
is Newton's constant, and
is the distance from the center of the Earth to the body's location, which is very nearly the radius of the Earth. Setting this equal to
, the body's mass
cancels from both sides of the equation, leaving an acceleration that depends upon
,
, and
, and
can be taken to be constant. This particular value of acceleration is typically denoted
:
If the body is not released from rest but instead launched upwards and/or horizontally with nonzero velocity, then free fall becomes
projectile motion
Projectile motion is a form of motion experienced by an object or particle (a projectile) that is projected in a gravitational field, such as from Earth's surface, and moves along a curved path under the action of gravity only. In the particul ...
. When air resistance can be neglected, projectiles follow
parabola
In mathematics, a parabola is a plane curve which is Reflection symmetry, mirror-symmetrical and is approximately U-shaped. It fits several superficially different Mathematics, mathematical descriptions, which can all be proved to define exact ...
-shaped trajectories, because gravity affects the body's vertical motion and not its horizontal. At the peak of the projectile's trajectory, its vertical velocity is zero, but its acceleration is
downwards, as it is at all times. Setting the wrong vector equal to zero is a common confusion among physics students.
Uniform circular motion

When a body is in uniform circular motion, the force on it changes the direction of its motion but not its speed. For a body moving in a circle of radius
at a constant speed
, its acceleration has a magnitude
and is directed toward the center of the circle. The force required to sustain this acceleration, called the
centripetal force, is therefore also directed toward the center of the circle and has magnitude
. Many
orbits, such as that of the Moon around the Earth, can be approximated by uniform circular motion. In such cases, the centripetal force is gravity, and by Newton's law of universal gravitation has magnitude
, where
is the mass of the larger body being orbited. Therefore, the mass of a body can be calculated from observations of another body orbiting around it.
Newton's cannonball is a
thought experiment that interpolates between projectile motion and uniform circular motion. A cannonball that is lobbed weakly off the edge of a tall cliff will hit the ground in the same amount of time as if it were dropped from rest, because the force of gravity only affects the cannonball's momentum in the downward direction, and its effect is not diminished by horizontal movement. If the cannonball is launched with a greater initial horizontal velocity, then it will travel farther before it hits the ground, but it will still hit the ground in the same amount of time. However, if the cannonball is launched with an even larger initial velocity, then the curvature of the Earth becomes significant: the ground itself will curve away from the falling cannonball. A very fast cannonball will fall away from the inertial straight-line trajectory at the same rate that the Earth curves away beneath it; in other words, it will be in orbit (imagining that it is not slowed by air resistance or obstacles).
Harmonic motion
Consider a body of mass
able to move along the
axis, and suppose an equilibrium point exists at the position
. That is, at
, the net force upon the body is the zero vector, and by Newton's second law, the body will not accelerate. If the force upon the body is proportional to the displacement from the equilibrium point, and directed to the equilibrium point, then the body will perform
simple harmonic motion
In mechanics and physics, simple harmonic motion (sometimes abbreviated ) is a special type of periodic motion of a body resulting from a dynamic equilibrium between an inertial force, proportional to the acceleration of the body away from the ...
. Writing the force as
, Newton's second law becomes
This differential equation has the solution
where the frequency
is equal to
, and the constants
and
can be calculated knowing, for example, the position and velocity the body has at a given time, like
.
One reason that the harmonic oscillator is a conceptually important example is that it is good approximation for many systems near a stable mechanical equilibrium. For example, a
pendulum has a stable equilibrium in the vertical position: if motionless there, it will remain there, and if pushed slightly, it will swing back and forth. Neglecting air resistance and friction in the pivot, the force upon the pendulum is gravity, and Newton's second law becomes
where
is the length of the pendulum and
is its angle from the vertical. When the angle
is small, the
sine of
is nearly equal to
(see
Taylor series), and so this expression simplifies to the equation for a simple harmonic oscillator with frequency
.
A harmonic oscillator can be ''damped,'' often by friction or viscous drag, in which case energy bleeds out of the oscillator and the amplitude of the oscillations decreases over time. Also, a harmonic oscillator can be ''driven'' by an applied force, which can lead to the phenomenon of
resonance.
Objects with variable mass

Newtonian physics treats matter as being neither created nor destroyed, though it may be rearranged. It can be the case that an object of interest gains or loses mass because matter is added to or removed from it. In such a situation, Newton's laws can be applied to the individual pieces of matter, keeping track of which pieces belong to the object of interest over time. For instance, if a rocket of mass
, moving at velocity
, ejects matter at a velocity
relative to the rocket, then
where
is the net external force (e.g., a planet's gravitational pull).
Rigid-body motion and rotation
A rigid body is an object whose size is too large to neglect and which maintains the same shape over time. In Newtonian mechanics, the motion of a rigid body is often understood by separating it into movement of the body's
center of mass and movement around the center of mass.
Center of mass

Significant aspects of the motion of an extended body can be understood by imagining the mass of that body concentrated to a single point, known as the center of mass. The location of a body's center of mass depends upon how that body's material is distributed. For a collection of pointlike objects with masses
at positions
, the center of mass is located at
where
is the total mass of the collection. In the absence of a net external force, the center of mass moves at a constant speed in a straight line. This applies, for example, to a collision between two bodies. If the total external force is not zero, then the center of mass changes velocity as though it were a point body of mass
. This follows from the fact that the internal forces within the collection, the forces that the objects exert upon each other, occur in balanced pairs by Newton's third law. In a system of two bodies with one much more massive than the other, the center of mass will approximately coincide with the location of the more massive body.
Rotational analogues of Newton's laws
When Newton's laws are applied to rotating extended bodies, they lead to new quantities that are analogous to those invoked in the original laws. The analogue of mass is the
moment of inertia, the counterpart of momentum is
angular momentum
In physics, angular momentum (rarely, moment of momentum or rotational momentum) is the rotational analog of linear momentum. It is an important physical quantity because it is a conserved quantity—the total angular momentum of a closed syst ...
, and the counterpart of force is
torque.
Angular momentum is calculated with respect to a reference point. If the displacement vector from a reference point to a body is
and the body has momentum
, then the body's angular momentum with respect to that point is, using the vector
cross product,
Taking the time derivative of the angular momentum gives
The first term vanishes because
and
point in the same direction. The remaining term is the torque,
When the torque is zero, the angular momentum is constant, just as when the force is zero, the momentum is constant.
The torque can vanish even when the force is non-zero, if the body is located at the reference point (
) or if the force
and the displacement vector
are directed along the same line.
The angular momentum of a collection of point masses, and thus of an extended body, is found by adding the contributions from each of the points. This provides a means to characterize a body's rotation about an axis, by adding up the angular momenta of its individual pieces. The result depends on the chosen axis, the shape of the body, and the rate of rotation.
Multi-body gravitational system

Newton's law of universal gravitation states that any body attracts any other body along the straight line connecting them. The size of the attracting force is proportional to the product of their masses, and inversely proportional to the square of the distance between them. Finding the shape of the orbits that an inverse-square force law will produce is known as the
Kepler problem. The Kepler problem can be solved in multiple ways, including by demonstrating that the
Laplace–Runge–Lenz vector
In classical mechanics, the Laplace–Runge–Lenz (LRL) vector is a vector used chiefly to describe the shape and orientation of the orbit of one astronomical body around another, such as a binary star or a planet revolving around a star. For t ...
is constant, or by applying a duality transformation to a 2-dimensional harmonic oscillator. However it is solved, the result is that orbits will be
conic sections, that is,
ellipses (including circles),
parabola
In mathematics, a parabola is a plane curve which is Reflection symmetry, mirror-symmetrical and is approximately U-shaped. It fits several superficially different Mathematics, mathematical descriptions, which can all be proved to define exact ...
s, or
hyperbolas. The
eccentricity
Eccentricity or eccentric may refer to:
* Eccentricity (behavior), odd behavior on the part of a person, as opposed to being "normal"
Mathematics, science and technology Mathematics
* Off-Centre (geometry), center, in geometry
* Eccentricity (g ...
of the orbit, and thus the type of conic section, is determined by the energy and the angular momentum of the orbiting body. Planets do not have sufficient energy to escape the Sun, and so their orbits are ellipses, to a good approximation; because the planets pull on one another, actual orbits are not exactly conic sections.
If a third mass is added, the Kepler problem becomes the three-body problem, which in general has no exact solution in
closed form. That is, there is no way to start from the differential equations implied by Newton's laws and, after a finite sequence of standard mathematical operations, obtain equations that express the three bodies' motions over time.
can be applied to obtain useful, albeit approximate, results for the three-body problem. The positions and velocities of the bodies can be stored in
variables within a computer's memory; Newton's laws are used to calculate how the velocities will change over a short interval of time, and knowing the velocities, the changes of position over that time interval can be computed. This process is
looped to calculate, approximately, the bodies' trajectories. Generally speaking, the shorter the time interval, the more accurate the approximation.
Chaos and unpredictability
Nonlinear dynamics
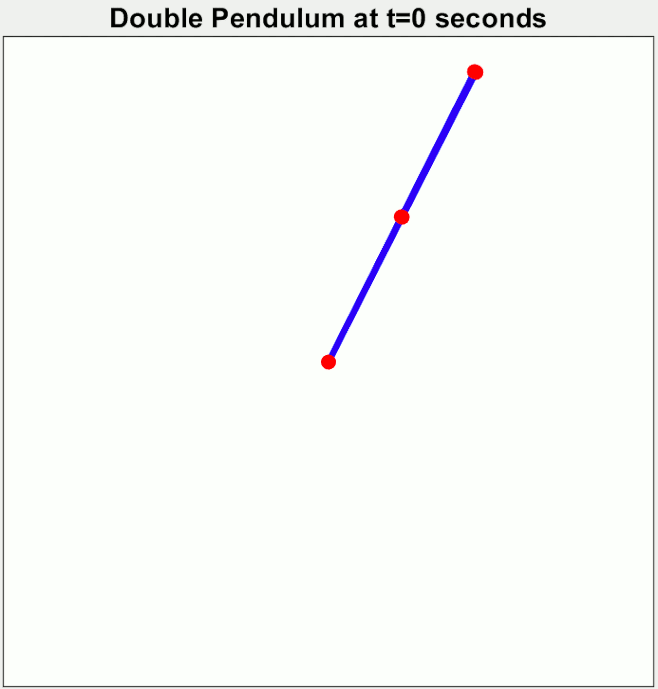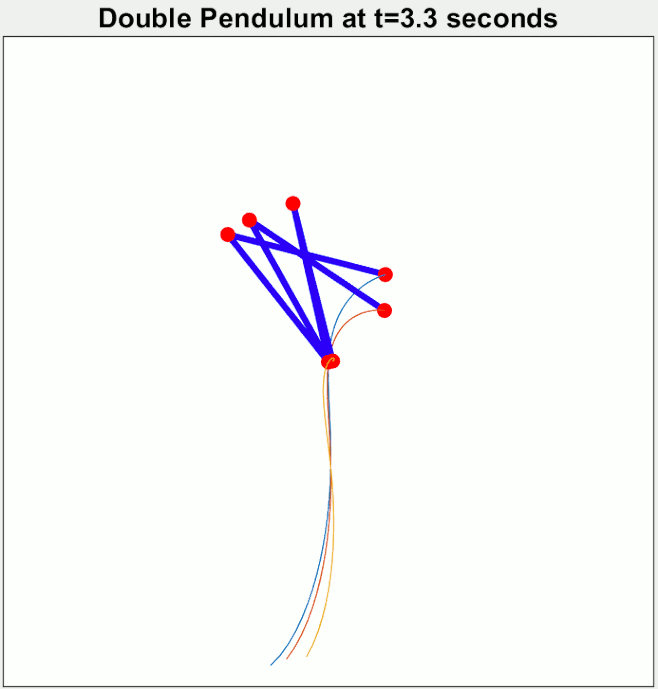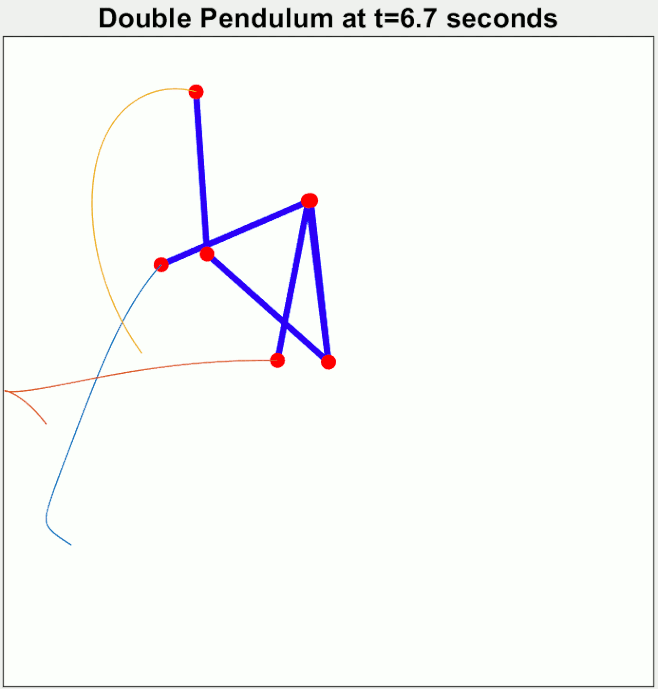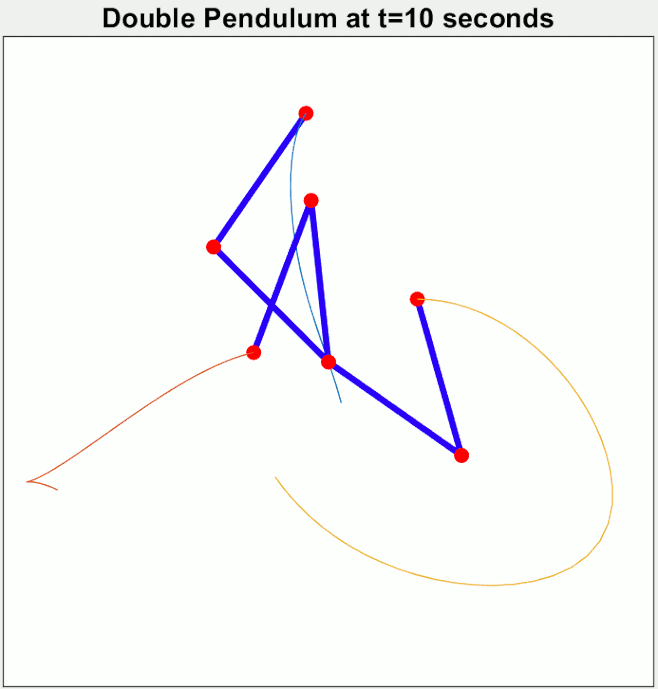
Newton's laws of motion allow the possibility of
chaos
Chaos or CHAOS may refer to:
Arts, entertainment and media Fictional elements
* Chaos (''Kinnikuman'')
* Chaos (''Sailor Moon'')
* Chaos (''Sesame Park'')
* Chaos (''Warhammer'')
* Chaos, in ''Fabula Nova Crystallis Final Fantasy''
* Cha ...
.
That is, qualitatively speaking, physical systems obeying Newton's laws can exhibit sensitive dependence upon their initial conditions: a slight change of the position or velocity of one part of a system can lead to the whole system behaving in a radically different way within a short time. Noteworthy examples include the three-body problem, the
double pendulum,
dynamical billiards
A dynamical billiard is a dynamical system in which a particle alternates between free motion (typically as a straight line) and specular reflections from a boundary. When the particle hits the boundary it reflects from it without loss of speed ...
, and the
Fermi–Pasta–Ulam–Tsingou problem
In physics, the Fermi–Pasta–Ulam–Tsingou problem or formerly the Fermi–Pasta–Ulam problem was the apparent paradox in chaos theory that many complicated enough physical systems exhibited almost exactly periodic behavior – called Fermi ...
.
Newton's laws can be applied to
fluids by considering a fluid as composed of infinitesimal pieces, each exerting forces upon neighboring pieces. The
Euler momentum equation is an expression of Newton's second law adapted to fluid dynamics.
A fluid is described by a velocity field, i.e., a function
that assigns a velocity vector to each point in space and time. A small object being carried along by the fluid flow can change velocity for two reasons: first, because the velocity field at its position is changing over time, and second, because it moves to a new location where the velocity field has a different value. Consequently, when Newton's second law is applied to an infinitesimal portion of fluid, the acceleration
has two terms, a combination known as a
''total'' or ''material'' derivative. The mass of an infinitesimal portion depends upon the fluid
density
Density (volumetric mass density or specific mass) is the substance's mass per unit of volume. The symbol most often used for density is ''ρ'' (the lower case Greek letter rho), although the Latin letter ''D'' can also be used. Mathematical ...
, and there is a net force upon it if the fluid pressure varies from one side of it to another. Accordingly,
becomes
where
is the density,
is the pressure, and
stands for an external influence like a gravitational pull. Incorporating the effect of
viscosity turns the Euler equation into a
Navier–Stokes equation:
where
is the
kinematic viscosity
The viscosity of a fluid is a measure of its resistance to deformation at a given rate. For liquids, it corresponds to the informal concept of "thickness": for example, syrup has a higher viscosity than water.
Viscosity quantifies the int ...
.
Singularities
It is mathematically possible for a collection of point masses, moving in accord with Newton's laws, to launch some of themselves away so forcefully that they fly off to infinity in a finite time. This unphysical behavior, known as a "noncollision singularity",
depends upon the masses being pointlike and able to approach one another arbitrarily closely, as well as the lack of a
relativistic speed limit in Newtonian physics.
It is not yet known whether or not the Euler and Navier–Stokes equations exhibit the analogous behavior of initially smooth solutions "blowing up" in finite time. The question of
existence and smoothness of Navier–Stokes solutions is one of the
Millennium Prize Problems
The Millennium Prize Problems are seven well-known complex mathematical problems selected by the Clay Mathematics Institute in 2000. The Clay Institute has pledged a US$1 million prize for the first correct solution to each problem. According ...
.
Relation to other formulations of classical physics
Classical mechanics can be mathematically formulated in multiple different ways, other than the "Newtonian" description (which itself, of course, incorporates contributions from others both before and after Newton). The physical content of these different formulations is the same as the Newtonian, but they provide different insights and facilitate different types of calculations. For example,
Lagrangian mechanics
In physics, Lagrangian mechanics is a formulation of classical mechanics founded on the stationary-action principle (also known as the principle of least action). It was introduced by the Italian-French mathematician and astronomer Joseph- ...
helps make apparent the connection between symmetries and conservation laws, and it is useful when calculating the motion of constrained bodies, like a mass restricted to move along a curving track or on the surface of a sphere.
Hamiltonian mechanics
Hamiltonian mechanics emerged in 1833 as a reformulation of Lagrangian mechanics. Introduced by Sir William Rowan Hamilton, Hamiltonian mechanics replaces (generalized) velocities \dot q^i used in Lagrangian mechanics with (generalized) ''momenta ...
is convenient for
statistical physics
Statistical physics is a branch of physics that evolved from a foundation of statistical mechanics, which uses methods of probability theory and statistics, and particularly the mathematical tools for dealing with large populations and approxim ...
,
leads to further insight about symmetry,
and can be developed into sophisticated techniques for
perturbation theory.
Due to the breadth of these topics, the discussion here will be confined to concise treatments of how they reformulate Newton's laws of motion.
Lagrangian
Lagrangian mechanics
In physics, Lagrangian mechanics is a formulation of classical mechanics founded on the stationary-action principle (also known as the principle of least action). It was introduced by the Italian-French mathematician and astronomer Joseph- ...
differs from the Newtonian formulation by considering entire trajectories at once rather than predicting a body's motion at a single instant.
It is traditional in Lagrangian mechanics to denote position with
and velocity with
. The simplest example is a massive point particle, the Lagrangian for which can be written as the difference between its kinetic and potential energies:
where the kinetic energy is
and the potential energy is some function of the position,
. The physical path that the particle will take between an initial point
and a final point
is the path for which the integral of the Lagrangian is "stationary". That is, the physical path has the property that small perturbations of it will, to a first approximation, not change the integral of the Lagrangian.
Calculus of variations provides the mathematical tools for finding this path.
Applying the calculus of variations to the task of finding the path yields the
Euler–Lagrange equation
In the calculus of variations and classical mechanics, the Euler–Lagrange equations are a system of second-order ordinary differential equations whose solutions are stationary points of the given action functional. The equations were discovered ...
for the particle,
Evaluating the
partial derivatives of the Lagrangian gives
which is a restatement of Newton's second law. The left-hand side is the time derivative of the momentum, and the right-hand side is the force, represented in terms of the potential energy.
argue that the Lagrangian formulation makes the conceptual content of classical mechanics more clear than starting with Newton's laws.
Lagrangian mechanics provides a convenient framework in which to prove
Noether's theorem
Noether's theorem or Noether's first theorem states that every differentiable symmetry of the action of a physical system with conservative forces has a corresponding conservation law. The theorem was proven by mathematician Emmy Noether ...
, which relates symmetries and conservation laws. The conservation of momentum can be derived by applying Noether's theorem to a Lagrangian for a multi-particle system, and so, Newton's third law is a theorem rather than an assumption.
Hamiltonian

In
Hamiltonian mechanics
Hamiltonian mechanics emerged in 1833 as a reformulation of Lagrangian mechanics. Introduced by Sir William Rowan Hamilton, Hamiltonian mechanics replaces (generalized) velocities \dot q^i used in Lagrangian mechanics with (generalized) ''momenta ...
, the dynamics of a system are represented by a function called the Hamiltonian, which in many cases of interest is equal to the total energy of the system.
The Hamiltonian is a function of the positions and the momenta of all the bodies making up the system, and it may also depend explicitly upon time. The time derivatives of the position and momentum variables are given by partial derivatives of the Hamiltonian, via
Hamilton's equations.
The simplest example is a point mass
constrained to move in a straight line, under the effect of a potential. Writing
for the position coordinate and
for the body's momentum, the Hamiltonian is
In this example, Hamilton's equations are
and
Evaluating these partial derivatives, the former equation becomes
which reproduces the familiar statement that a body's momentum is the product of its mass and velocity. The time derivative of the momentum is
which, upon identifying the negative derivative of the potential with the force, is just Newton's second law once again.
As in the Lagrangian formulation, in Hamiltonian mechanics the conservation of momentum can be derived using Noether's theorem, making Newton's third law an idea that is deduced rather than assumed.
Among the proposals to reform the standard introductory-physics curriculum is one that teaches the concept of energy before that of force, essentially "introductory Hamiltonian mechanics".
Hamilton–Jacobi
The
Hamilton–Jacobi equation
In physics, the Hamilton–Jacobi equation, named after William Rowan Hamilton and Carl Gustav Jacob Jacobi, is an alternative formulation of classical mechanics, equivalent to other formulations such as Newton's laws of motion, Lagrangian mecha ...
provides yet another formulation of classical mechanics, one which makes it mathematically analogous to
wave optics
In physics, physical optics, or wave optics, is the branch of optics that studies interference, diffraction, polarization, and other phenomena for which the ray approximation of geometric optics is not valid. This usage tends not to include effe ...
.
This formulation also uses Hamiltonian functions, but in a different way than the formulation described above. The paths taken by bodies or collections of bodies are deduced from a function
of positions
and time
. The Hamiltonian is incorporated into the Hamilton–Jacobi equation, a
differential equation
In mathematics, a differential equation is an equation that relates one or more unknown functions and their derivatives. In applications, the functions generally represent physical quantities, the derivatives represent their rates of change, an ...
for
. Bodies move over time in such a way that their trajectories are perpendicular to the surfaces of constant
, analogously to how a light ray propagates in the direction perpendicular to its wavefront. This is simplest to express for the case of a single point mass, in which
is a function
, and the point mass moves in the direction along which
changes most steeply. In other words, the momentum of the point mass is the
gradient of
:
The Hamilton–Jacobi equation for a point mass is
The relation to Newton's laws can be seen by considering a point mass moving in a time-independent potential
, in which case the Hamilton–Jacobi equation becomes
Taking the gradient of both sides, this becomes
Interchanging the order of the partial derivatives on the left-hand side, and using the
power
Power most often refers to:
* Power (physics), meaning "rate of doing work"
** Engine power, the power put out by an engine
** Electric power
* Power (social and political), the ability to influence people or events
** Abusive power
Power may a ...
and
chain rule
In calculus, the chain rule is a formula that expresses the derivative of the composition of two differentiable functions and in terms of the derivatives of and . More precisely, if h=f\circ g is the function such that h(x)=f(g(x)) for every , ...
s on the first term on the right-hand side,
Gathering together the terms that depend upon the gradient of
,
This is another re-expression of Newton's second law. The expression in brackets is a
''total'' or ''material'' derivative as mentioned above, in which the first term indicates how the function being differentiated changes over time at a fixed location, and the second term captures how a moving particle will see different values of that function as it travels from place to place:
Relation to other physical theories
Thermodynamics and statistical physics

In
statistical physics
Statistical physics is a branch of physics that evolved from a foundation of statistical mechanics, which uses methods of probability theory and statistics, and particularly the mathematical tools for dealing with large populations and approxim ...
, the
kinetic theory of gases applies Newton's laws of motion to large numbers (typically on the order of
Avogadro's number) of particles. Kinetic theory can explain, for example, the
pressure that a gas exerts upon the container holding it as the aggregate of many impacts of atoms, each imparting a tiny amount of momentum.
The
Langevin equation is a special case of Newton's second law, adapted for the case of describing a small object bombarded stochastically by even smaller ones.
It can be written
where
is a
drag coefficient
In fluid dynamics, the drag coefficient (commonly denoted as: c_\mathrm, c_x or c_) is a dimensionless quantity that is used to quantify the drag or resistance of an object in a fluid environment, such as air or water. It is used in the drag e ...
and
is a force that varies randomly from instant to instant, representing the net effect of collisions with the surrounding particles. This is used to model
Brownian motion
Brownian motion, or pedesis (from grc, πήδησις "leaping"), is the random motion of particles suspended in a medium (a liquid or a gas).
This pattern of motion typically consists of random fluctuations in a particle's position insi ...
.
Electromagnetism
Newton's three laws can be applied to phenomena involving
electricity and
magnetism, though subtleties and caveats exist.
Coulomb's law for the electric force between two stationary,
electrically charged bodies has much the same mathematical form as Newton's law of universal gravitation: the force is proportional to the product of the charges, inversely proportional to the square of the distance between them, and directed along the straight line between them. The Coulomb force that a charge
exerts upon a charge
is equal in magnitude to the force that
exerts upon
, and it points in the exact opposite direction. Coulomb's law is thus consistent with Newton's third law.
Electromagnetism treats forces as produced by ''fields'' acting upon charges. The
Lorentz force law provides an expression for the force upon a charged body that can be plugged into Newton's second law in order to calculate its acceleration. According to the Lorentz force law, a charged body in an electric field experiences a force in the direction of that field, a force proportional to its charge
and to the strength of the electric field. In addition, a ''moving'' charged body in a magnetic field experiences a force that is also proportional to its charge, in a direction perpendicular to both the field and the body's direction of motion. Using the vector
cross product,
If the electric field vanishes (
), then the force will be perpendicular to the charge's motion, just as in the case of uniform circular motion studied above, and the charge will circle (or more generally move in a
helix
A helix () is a shape like a corkscrew or spiral staircase. It is a type of smooth space curve with tangent lines at a constant angle to a fixed axis. Helices are important in biology, as the DNA molecule is formed as two intertwined helic ...
) around the magnetic field lines at the
cyclotron frequency
Cyclotron resonance describes the interaction of external forces with charged particles experiencing a magnetic field, thus already moving on a circular path. It is named after the cyclotron, a cyclic particle accelerator that utilizes an oscillati ...
.
works by applying electric and/or magnetic fields to moving charges and measuring the resulting acceleration, which by the Lorentz force law yields the
mass-to-charge ratio.
Collections of charged bodies do not always obey Newton's third law: there can be a change of one body's momentum without a compensatory change in the momentum of another. The discrepancy is accounted for by momentum carried by the electromagnetic field itself. The momentum per unit volume of the electromagnetic field is proportional to the
Poynting vector.
There is subtle conceptual conflict between electromagnetism and Newton's first law:
Maxwell's theory of electromagnetism
In physics, electromagnetism is an interaction that occurs between particles with electric charge. It is the second-strongest of the four fundamental interactions, after the strong force, and it is the dominant force in the interactions o ...
predicts that electromagnetic waves will travel through empty space at a constant, definite speed. Thus, some inertial observers seemingly have a privileged status over the others, namely those who measure the
speed of light and find it to be the value predicted by the Maxwell equations. In other words, light provides an absolute standard for speed, yet the principle of inertia holds that there should be no such standard. This tension is resolved in the theory of special relativity, which revises the notions of ''space'' and ''time'' in such a way that all inertial observers will agree upon the speed of light in vacuum.
Special relativity
In special relativity, the rule that Wilczek called "Newton's Zeroth Law" breaks down: the mass of a composite object is not merely the sum of the masses of the individual pieces.
Newton's first law, inertial motion, remains true. A form of Newton's second law, that force is the rate of change of momentum, also holds, as does the conservation of momentum. However, the definition of momentum is modified. Among the consequences of this is the fact that the more quickly a body moves, the harder it is to accelerate, and so, no matter how much force is applied, a body cannot be accelerated to the speed of light. Depending on the problem at hand, momentum in special relativity can be represented as a three-dimensional vector,
, where
is the body's
rest mass
The invariant mass, rest mass, intrinsic mass, proper mass, or in the case of bound systems simply mass, is the portion of the total mass of an object or system of objects that is independent of the overall motion of the system. More precisely, i ...
and
is the
Lorentz factor
The Lorentz factor or Lorentz term is a quantity expressing how much the measurements of time, length, and other physical properties change for an object while that object is moving. The expression appears in several equations in special relativit ...
, which depends upon the body's speed. Alternatively, momentum and force can be represented as
four-vector
In special relativity, a four-vector (or 4-vector) is an object with four components, which transform in a specific way under Lorentz transformations. Specifically, a four-vector is an element of a four-dimensional vector space considered as a ...
s.
Newtonian mechanics is a good approximation to special relativity when the speeds involved are small compared to that of light.
General relativity
General relativity
General relativity, also known as the general theory of relativity and Einstein's theory of gravity, is the geometric theory of gravitation published by Albert Einstein in 1915 and is the current description of gravitation in modern physics ...
is theory of gravity that advances beyond that of Newton. In general relativity, gravitational force is reimagined as curvature of
spacetime. A curved path like an orbit is not the result of a force deflecting a body from an ideal straight-line path, but rather the body's attempt to fall freely through a background that is itself curved by the presence of other masses. A remark by
John Archibald Wheeler
John Archibald Wheeler (July 9, 1911April 13, 2008) was an American theoretical physicist. He was largely responsible for reviving interest in general relativity in the United States after World War II. Wheeler also worked with Niels Bohr in ...
that has become proverbial among physicists summarizes the theory: "Spacetime tells matter how to move; matter tells spacetime how to curve."
Wheeler himself thought of this reciprocal relationship as a modern, generalized form of Newton's third law.
The relation between matter distribution and spacetime curvature is given by the
Einstein field equations
In the general theory of relativity, the Einstein field equations (EFE; also known as Einstein's equations) relate the geometry of spacetime to the distribution of matter within it.
The equations were published by Einstein in 1915 in the form ...
, which require
tensor calculus
In mathematics, tensor calculus, tensor analysis, or Ricci calculus is an extension of vector calculus to tensor fields (tensors that may vary over a manifold, e.g. in spacetime).
Developed by Gregorio Ricci-Curbastro and his student Tullio Levi ...
to express.
The Newtonian theory of gravity is a good approximation to the predictions of general relativity when gravitational effects are weak and objects are moving slowly compared to the speed of light.
Quantum mechanics
Quantum mechanics
Quantum mechanics is a fundamental theory in physics that provides a description of the physical properties of nature at the scale of atoms and subatomic particles. It is the foundation of all quantum physics including quantum chemistr ...
is a theory of physics originally developed in order to understand microscopic phenomena: behavior at the scale of molecules, atoms or subatomic particles. Generally and loosely speaking, the smaller a system is, the more an adequate mathematical model will require understanding quantum effects. The conceptual underpinning of quantum physics is
very different from that of classical physics. Instead of thinking about quantities like position, momentum, and energy as properties that an object ''has'', one considers what result might ''appear'' when a
measurement of a chosen type is performed. Quantum mechanics allows the physicist to calculate the probability that a chosen measurement will elicit a particular result. The
expectation value
In probability theory, the expected value (also called expectation, expectancy, mathematical expectation, mean, average, or first moment) is a generalization of the weighted average. Informally, the expected value is the arithmetic mean of a l ...
for a measurement is the average of the possible results it might yield, weighted by their probabilities of occurrence.
The
Ehrenfest theorem provides a connection between quantum expectation values and Newton's second law, a connection that is necessarily inexact, as quantum physics is fundamentally different from classical. In quantum physics, position and momentum are represented by mathematical entities known as
Hermitian operators, and the
Born rule
The Born rule (also called Born's rule) is a key postulate of quantum mechanics which gives the probability that a measurement of a quantum system will yield a given result. In its simplest form, it states that the probability density of findi ...
is used to calculate the expectation values of a position measurement or a momentum measurement. These expectation values will generally change over time; that is, depending on the time at which (for example) a position measurement is performed, the probabilities for its different possible outcomes will vary. The Ehrenfest theorem says, roughly speaking, that the equations describing how these expectation values change over time have a form reminiscent of Newton's second law. However, the more pronounced quantum effects are in a given situation, the more difficult it is to derive meaningful conclusions from this resemblance.
History
The concepts invoked in Newton's laws of motion — mass, velocity, momentum, force — have predecessors in earlier work, and the content of Newtonian physics was further developed after Newton's time. Newton combined knowledge of celestial motions with the study of events on Earth and showed that one theory of mechanics could encompass both.
Antiquity and medieval background
The subject of physics is often traced back to
Aristotle
Aristotle (; grc-gre, Ἀριστοτέλης ''Aristotélēs'', ; 384–322 BC) was a Greek philosopher and polymath during the Classical period in Ancient Greece. Taught by Plato, he was the founder of the Peripatetic school of ph ...
; however, the history of the concepts involved is obscured by multiple factors. An exact correspondence between Aristotelian and modern concepts is not simple to establish: Aristotle did not clearly distinguish what we would call speed and force, and he used the same term for
density
Density (volumetric mass density or specific mass) is the substance's mass per unit of volume. The symbol most often used for density is ''ρ'' (the lower case Greek letter rho), although the Latin letter ''D'' can also be used. Mathematical ...
and
viscosity; he conceived of motion as always through a medium, rather than through space. In addition, some concepts often termed "Aristotelian" might better be attributed to his followers and commentators upon him. These commentators found that Aristotelian physics had difficulty explaining projectile motion. Aristotle divided motion into two types: "natural" and "violent". The "natural" motion of terrestrial solid matter was to fall downwards, whereas a "violent" motion could push a body sideways. Moreover, in Aristotelian physics, a "violent" motion requires an immediate cause; separated from the cause of its "violent" motion, a body would revert to its "natural" behavior. Yet a javelin continues moving after it leaves the hand of its thrower. Aristotle concluded that the air around the javelin must be imparted with the ability to move the javelin forward.
John Philoponus
John Philoponus (Greek: ; ; c. 490 – c. 570), also known as John the Grammarian or John of Alexandria, was a Byzantine Greek philologist, Aristotelian commentator, Christian theologian and an author of a considerable number of philosophical tr ...
, a
Byzantine Greek thinker active during the sixth century, found this absurd: the same medium, air, was somehow responsible both for sustaining motion and for impeding it. If Aristotle's idea were true, Philoponus said, armies would launch weapons by blowing upon them with bellows. Philoponus argued that setting a body into motion imparted a quality,
impetus, that would be contained within the body itself. As long as its impetus was sustained, the body would continue to move. In the following centuries, versions of impetus theory were advanced by individuals including
Nur ad-Din al-Bitruji,
Avicenna,
Abu'l-Barakāt al-Baghdādī
Abu'l-Barakāt Hibat Allah ibn Malkā al-Baghdādī ( ar, أبو البركات هبة الله بن ملكا البغدادي; c. 1080 – 1164 or 1165 CE) was an Islamic philosopher, physician and physicist of Jewish descent from Baghdad, Iraq. ...
,
John Buridan, and
Albert of Saxony. In retrospect, the idea of impetus can be seen as a forerunner of the modern concept of momentum. (The intuition that objects move according to some kind of impetus persists in many students of introductory physics.)
Inertia and the first law
The modern concept of inertia is credited to
Galileo. Based on his experiments, Galileo concluded that the "natural" behavior of a moving body was to keep moving, until something else interfered with it. Galileo recognized that in projectile motion, the Earth's gravity affects vertical but not horizontal motion. However, Galileo's idea of inertia was not exactly the one that would be codified into Newton's first law. Galileo thought that a body moving a long distance inertially would follow the curve of the Earth. This idea was corrected by
Isaac Beeckman
Isaac Beeckman (10 December 1588van Berkel, p10 – 19 May 1637) was a Dutch philosopher and scientist, who, through his studies and contact with leading natural philosophers, may have "virtually given birth to modern atomism".Harold J. Cook, in ...
,
René Descartes, and
Pierre Gassendi, who recognized that inertial motion should be motion in a straight line.
Force and the second law
Christiaan Huygens, in his ''
Horologium Oscillatorium
(English: ''The Pendulum Clock: or Geometrical Demonstrations Concerning the Motion of Pendula as Applied to Clocks'') is a book published by Dutch physicist Christiaan Huygens in 1673 and his major work on pendulums and horology. It is regarde ...
'' (1673), put forth the hypothesis that "By the action of gravity, whatever its sources, it happens that bodies are moved by a motion composed both of a uniform motion in one direction or another and of a motion downward due to gravity." Newton's second law generalized this hypothesis from gravity to all forces.
One important characteristic of Newtonian physics is that forces can
act at a distance without requiring physical contact. For example, the Sun and the Earth pull on each other gravitationally, despite being separated by millions of kilometres. This contrasts with the idea, championed by Descartes among others, that the Sun's gravity held planets in orbit by swirling them in a vortex of transparent matter, ''
aether''. Newton considered aetherial explanations of force but ultimately rejected them.
The study of magnetism by
William Gilbert and others created a precedent for thinking of ''immaterial'' forces,
and unable to find a quantitatively satisfactory explanation of his law of gravity in terms of an aetherial model, Newton eventually declared, "
I feign no hypotheses": whether or not a model like Descartes's vortices could be found to underlie the ''Principia''
's theories of motion and gravity, the first grounds for judging them must be the successful predictions they made. And indeed, since Newton's time
every attempt at such a model has failed.
Momentum conservation and the third law
Johannes Kepler suggested that gravitational attractions were reciprocal — that, for example, the Moon pulls on the Earth while the Earth pulls on the Moon — but he did not argue that such pairs are equal and opposite. In his ''
Principles of Philosophy'' (1644), Descartes introduced the idea that during a collision between bodies, a "quantity of motion" remains unchanged. Descartes defined this quantity somewhat imprecisely by adding up the products of the speed and "size" of each body, where "size" for him incorporated both volume and surface area. Moreover, Descartes thought of the universe as a
plenum
Plenum may refer to:
* Plenum chamber, a chamber intended to contain air, gas, or liquid at positive pressure
* Plenism, or ''Horror vacui'' (physics) the concept that "nature abhors a vacuum"
* Plenum (meeting), a meeting of a deliberative asse ...
, that is, filled with matter, so all motion required a body to displace a medium as it moved. During the 1650s, Huygens studied collisions between hard spheres and deduced a principle that is now identified as the conservation of momentum.
Christopher Wren would later deduce the same rules for
elastic collisions that Huygens had, and
John Wallis would apply momentum conservation to study
inelastic collisions
An inelastic collision, in contrast to an elastic collision, is a collision in which kinetic energy is not conserved due to the action of internal friction.
In collisions of macroscopic bodies, some kinetic energy is turned into vibrational energ ...
. Newton cited the work of Huygens, Wren, and Wallis to support the validity of his third law.
Newton arrived at his set of three laws incrementally. In a
1684 manuscript written to Huygens, he listed four laws: the principle of inertia, the change of motion by force, a statement about relative motion that would today be called
Galilean invariance
Galilean invariance or Galilean relativity states that the laws of motion are the same in all inertial frames of reference. Galileo Galilei first described this principle in 1632 in his ''Dialogue Concerning the Two Chief World Systems'' using th ...
, and the rule that interactions between bodies do not change the motion of their center of mass. In a later manuscript, Newton added a law of action and reaction, while saying that this law and the law regarding the center of mass implied one another. Newton probably settled on the presentation in the ''Principia,'' with three primary laws and then other statements reduced to corollaries, during 1685.
After the ''Principia''
Newton expressed his second law by saying that the force on a body is proportional to its change of motion, or momentum. By the time he wrote the ''Principia,'' he had already developed calculus (which he called "
the science of fluxions"), but in the ''Principia'' he made no explicit use of it, perhaps because he believed geometrical arguments in the tradition of
Euclid to be more rigorous. Consequently, the ''Principia'' does not express acceleration as the second derivative of position, and so it does not give the second law as
. This form of the second law was written (for the special case of constant force) at least as early as 1716, by
Jakob Hermann
Jakob Hermann (16 July 1678 – 11 July 1733) was a mathematician who worked on problems in classical mechanics. He is the author of ''Phoronomia'', an early treatise on Mechanics in Latin, which has been translated by Ian Bruce in 2015-16. In 172 ...
;
Leonhard Euler would employ it as a basic premise in the 1740s. Euler pioneered the study of rigid bodies and established the basic theory of fluid dynamics.
Pierre-Simon Laplace's five-volume ''
Traité de mécanique céleste'' (1798–1825) forsook geometry and developed mechanics purely through algebraic expressions, while resolving questions that the ''Principia'' had left open, like a full theory of the
tides.
The concept of energy became a key part of Newtonian mechanics in the post-Newton period. Huygens' solution of the collision of hard spheres showed that in that case, not only is momentum conserved, but kinetic energy is as well (or, rather, a quantity that in retrospect we can identify as one-half the total kinetic energy). The question of what is conserved during all other processes, like inelastic collisions and motion slowed by friction, was not resolved until the 19th century. Debates on this topic overlapped with philosophical disputes between the metaphysical views of Newton and Leibniz, and variants of the term "force" were sometimes used to denote what we would call types of energy. For example, in 1742,
Émilie du Châtelet wrote, "Dead force consists of a simple tendency to motion: such is that of a spring ready to relax;
living force is that which a body has when it is in actual motion." In modern terminology, "dead force" and "living force" correspond to potential energy and kinetic energy respectively. Conservation of energy was not established as a universal principle until it was understood that the energy of mechanical work can be dissipated into heat. With the concept of energy given a solid grounding, Newton's laws could then be derived within formulations of classical mechanics that put energy first, as in the Lagrangian and Hamiltonian formulations described above.
Modern presentations of Newton's laws use the mathematics of vectors, a topic that was not developed until the late 19th and early 20th centuries. Vector algebra, pioneered by
Josiah Willard Gibbs and
Oliver Heaviside, stemmed from and largely supplanted the earlier system of
quaternions invented by
William Rowan Hamilton.
See also
*
History of classical mechanics
This article deals with the history of classical mechanics.
Precursors to classical mechanics
Antiquity
The ancient Greek philosophers, Aristotle in particular, were among the first to propose that abstract principles govern nature. Aris ...
*
List of eponymous laws
*
List of equations in classical mechanics
Classical mechanics is the branch of physics used to describe the motion of macroscopic objects. It is the most familiar of the theories of physics. The concepts it covers, such as mass, acceleration, and force, are commonly used and known. The sub ...
*
List of scientific laws named after people
*
List of textbooks on classical mechanics and quantum mechanics
*
Norton's dome
Notes
References
Further reading
*
*
{{DEFAULTSORT:Newton's Laws Of Motion
Classical mechanics
Isaac Newton
Latin texts
Equations of physics
Scientific observation
Experimental physics
Copernican Revolution
Articles containing video clips
Scientific laws
 Newton's laws of motion are three basic
Newton's laws of motion are three basic  Translated from the Latin, Newton's first law reads,
:''Every body continues in its state of rest, or of uniform motion in a straight line, unless it is compelled to change that state by forces impressed upon it.''
Newton's first law expresses the principle of
Translated from the Latin, Newton's first law reads,
:''Every body continues in its state of rest, or of uniform motion in a straight line, unless it is compelled to change that state by forces impressed upon it.''
Newton's first law expresses the principle of  Overly brief paraphrases of the third law, like "action equals
Overly brief paraphrases of the third law, like "action equals  When a body is in uniform circular motion, the force on it changes the direction of its motion but not its speed. For a body moving in a circle of radius at a constant speed , its acceleration has a magnitudeand is directed toward the center of the circle. The force required to sustain this acceleration, called the centripetal force, is therefore also directed toward the center of the circle and has magnitude . Many orbits, such as that of the Moon around the Earth, can be approximated by uniform circular motion. In such cases, the centripetal force is gravity, and by Newton's law of universal gravitation has magnitude , where is the mass of the larger body being orbited. Therefore, the mass of a body can be calculated from observations of another body orbiting around it.
Newton's cannonball is a thought experiment that interpolates between projectile motion and uniform circular motion. A cannonball that is lobbed weakly off the edge of a tall cliff will hit the ground in the same amount of time as if it were dropped from rest, because the force of gravity only affects the cannonball's momentum in the downward direction, and its effect is not diminished by horizontal movement. If the cannonball is launched with a greater initial horizontal velocity, then it will travel farther before it hits the ground, but it will still hit the ground in the same amount of time. However, if the cannonball is launched with an even larger initial velocity, then the curvature of the Earth becomes significant: the ground itself will curve away from the falling cannonball. A very fast cannonball will fall away from the inertial straight-line trajectory at the same rate that the Earth curves away beneath it; in other words, it will be in orbit (imagining that it is not slowed by air resistance or obstacles).
When a body is in uniform circular motion, the force on it changes the direction of its motion but not its speed. For a body moving in a circle of radius at a constant speed , its acceleration has a magnitudeand is directed toward the center of the circle. The force required to sustain this acceleration, called the centripetal force, is therefore also directed toward the center of the circle and has magnitude . Many orbits, such as that of the Moon around the Earth, can be approximated by uniform circular motion. In such cases, the centripetal force is gravity, and by Newton's law of universal gravitation has magnitude , where is the mass of the larger body being orbited. Therefore, the mass of a body can be calculated from observations of another body orbiting around it.
Newton's cannonball is a thought experiment that interpolates between projectile motion and uniform circular motion. A cannonball that is lobbed weakly off the edge of a tall cliff will hit the ground in the same amount of time as if it were dropped from rest, because the force of gravity only affects the cannonball's momentum in the downward direction, and its effect is not diminished by horizontal movement. If the cannonball is launched with a greater initial horizontal velocity, then it will travel farther before it hits the ground, but it will still hit the ground in the same amount of time. However, if the cannonball is launched with an even larger initial velocity, then the curvature of the Earth becomes significant: the ground itself will curve away from the falling cannonball. A very fast cannonball will fall away from the inertial straight-line trajectory at the same rate that the Earth curves away beneath it; in other words, it will be in orbit (imagining that it is not slowed by air resistance or obstacles).
 Newtonian physics treats matter as being neither created nor destroyed, though it may be rearranged. It can be the case that an object of interest gains or loses mass because matter is added to or removed from it. In such a situation, Newton's laws can be applied to the individual pieces of matter, keeping track of which pieces belong to the object of interest over time. For instance, if a rocket of mass , moving at velocity , ejects matter at a velocity relative to the rocket, then
where is the net external force (e.g., a planet's gravitational pull).
Newtonian physics treats matter as being neither created nor destroyed, though it may be rearranged. It can be the case that an object of interest gains or loses mass because matter is added to or removed from it. In such a situation, Newton's laws can be applied to the individual pieces of matter, keeping track of which pieces belong to the object of interest over time. For instance, if a rocket of mass , moving at velocity , ejects matter at a velocity relative to the rocket, then
where is the net external force (e.g., a planet's gravitational pull).
 Significant aspects of the motion of an extended body can be understood by imagining the mass of that body concentrated to a single point, known as the center of mass. The location of a body's center of mass depends upon how that body's material is distributed. For a collection of pointlike objects with masses at positions , the center of mass is located at where is the total mass of the collection. In the absence of a net external force, the center of mass moves at a constant speed in a straight line. This applies, for example, to a collision between two bodies. If the total external force is not zero, then the center of mass changes velocity as though it were a point body of mass . This follows from the fact that the internal forces within the collection, the forces that the objects exert upon each other, occur in balanced pairs by Newton's third law. In a system of two bodies with one much more massive than the other, the center of mass will approximately coincide with the location of the more massive body.
Significant aspects of the motion of an extended body can be understood by imagining the mass of that body concentrated to a single point, known as the center of mass. The location of a body's center of mass depends upon how that body's material is distributed. For a collection of pointlike objects with masses at positions , the center of mass is located at where is the total mass of the collection. In the absence of a net external force, the center of mass moves at a constant speed in a straight line. This applies, for example, to a collision between two bodies. If the total external force is not zero, then the center of mass changes velocity as though it were a point body of mass . This follows from the fact that the internal forces within the collection, the forces that the objects exert upon each other, occur in balanced pairs by Newton's third law. In a system of two bodies with one much more massive than the other, the center of mass will approximately coincide with the location of the more massive body.
 Newton's law of universal gravitation states that any body attracts any other body along the straight line connecting them. The size of the attracting force is proportional to the product of their masses, and inversely proportional to the square of the distance between them. Finding the shape of the orbits that an inverse-square force law will produce is known as the Kepler problem. The Kepler problem can be solved in multiple ways, including by demonstrating that the
Newton's law of universal gravitation states that any body attracts any other body along the straight line connecting them. The size of the attracting force is proportional to the product of their masses, and inversely proportional to the square of the distance between them. Finding the shape of the orbits that an inverse-square force law will produce is known as the Kepler problem. The Kepler problem can be solved in multiple ways, including by demonstrating that the  Newton's laws of motion allow the possibility of
Newton's laws of motion allow the possibility of  In
In  In
In