Molecular orbital on:
[Wikipedia]
[Google]
[Amazon]
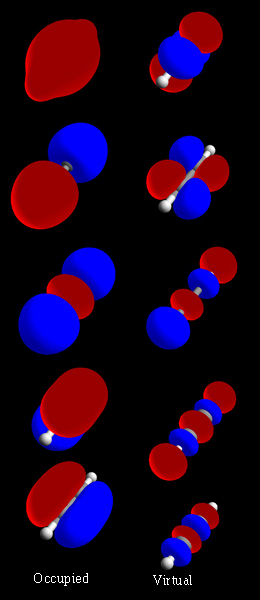 In chemistry, a molecular orbital is a
In chemistry, a molecular orbital is a
'' is symmetric), while an antibonding MO with σ-symmetry the orbital is σu, because inversion of s' – s'' is antisymmetric.
For a bonding MO with π-symmetry the orbital is πu because inversion through the center of symmetry for would produce a sign change (the two p atomic orbitals are in phase with each other but the two lobes have opposite signs), while an antibonding MO with π-symmetry is πg because inversion through the center of symmetry for would not produce a sign change (the two p orbitals are antisymmetric by phase).
 As a simple MO example, consider the electrons in a
As a simple MO example, consider the electrons in a
 In chemistry, a molecular orbital is a
In chemistry, a molecular orbital is a mathematical function
In mathematics, a function from a set to a set assigns to each element of exactly one element of .; the words map, mapping, transformation, correspondence, and operator are often used synonymously. The set is called the domain of the functi ...
describing the location and wave-like behavior of an electron
The electron ( or ) is a subatomic particle with a negative one elementary electric charge. Electrons belong to the first generation of the lepton particle family,
and are generally thought to be elementary particles because they have no ...
in a molecule
A molecule is a group of two or more atoms held together by attractive forces known as chemical bonds; depending on context, the term may or may not include ions which satisfy this criterion. In quantum physics, organic chemistry, and bioche ...
. This function can be used to calculate chemical and physical properties such as the probability of finding an electron
The electron ( or ) is a subatomic particle with a negative one elementary electric charge. Electrons belong to the first generation of the lepton particle family,
and are generally thought to be elementary particles because they have no ...
in any specific region. The terms ''atomic orbital'' and ''molecular orbital'' were introduced by Robert S. Mulliken
Robert Sanderson Mulliken Note Longuet-Higgins' amusing title for reference B238 1965 on page 354 of this Biographical Memoir. The title should be "Selected papers of Robert S Mulliken." (June 7, 1896 – October 31, 1986) was an American ph ...
in 1932 to mean ''one-electron orbital wave functions''. At an elementary level, they are used to describe the ''region'' of space in which a function has a significant amplitude.
In an isolated atom
Every atom is composed of a nucleus and one or more electrons bound to the nucleus. The nucleus is made of one or more protons and a number of neutrons. Only the most common variety of hydrogen has no neutrons.
Every solid, liquid, gas, ...
, the orbital electrons' location is determined by functions called atomic orbital
In atomic theory and quantum mechanics, an atomic orbital is a function describing the location and wave-like behavior of an electron in an atom. This function can be used to calculate the probability of finding any electron of an atom in an ...
s. When multiple atoms combine chemically into a molecule
A molecule is a group of two or more atoms held together by attractive forces known as chemical bonds; depending on context, the term may or may not include ions which satisfy this criterion. In quantum physics, organic chemistry, and bioche ...
, the electrons' locations are determined by the molecule as a whole, so the atomic orbitals combine to form molecular orbitals. The electrons from the constituent atoms occupy the molecular orbitals. Mathematically, molecular orbitals are an approximate solution to the Schrödinger equation
The Schrödinger equation is a linear partial differential equation that governs the wave function of a quantum-mechanical system. It is a key result in quantum mechanics, and its discovery was a significant landmark in the development of th ...
for the electrons in the field of the molecule's atomic nuclei. They are usually constructed by combining atomic orbital
In atomic theory and quantum mechanics, an atomic orbital is a function describing the location and wave-like behavior of an electron in an atom. This function can be used to calculate the probability of finding any electron of an atom in an ...
s or hybrid orbitals from each atom
Every atom is composed of a nucleus and one or more electrons bound to the nucleus. The nucleus is made of one or more protons and a number of neutrons. Only the most common variety of hydrogen has no neutrons.
Every solid, liquid, gas, ...
of the molecule, or other molecular orbitals from groups of atoms. They can be quantitatively calculated using the Hartree–Fock or self-consistent field (SCF) methods.
Molecular orbitals are of three types: ''bonding orbital
In theoretical chemistry, the bonding orbital is used in molecular orbital (MO) theory to describe the attractive interactions between the atomic orbitals of two or more atoms in a molecule. In MO theory, electrons are portrayed to move in waves. ...
s'' which have an energy lower than the energy of the atomic orbitals which formed them, and thus promote the chemical bonds which hold the molecule together; '' antibonding orbitals'' which have an energy higher than the energy of their constituent atomic orbitals, and so oppose the bonding of the molecule, and ''non-bonding orbital
A non-bonding orbital, also known as ''non-bonding molecular orbital'' (NBMO), is a molecular orbital whose occupation by electrons neither increases nor decreases the bond order between the involved atoms. Non-bonding orbitals are often designat ...
s'' which have the same energy as their constituent atomic orbitals and thus have no effect on the bonding of the molecule.
Overview
A molecular orbital (MO) can be used to represent the regions in amolecule
A molecule is a group of two or more atoms held together by attractive forces known as chemical bonds; depending on context, the term may or may not include ions which satisfy this criterion. In quantum physics, organic chemistry, and bioche ...
where an electron
The electron ( or ) is a subatomic particle with a negative one elementary electric charge. Electrons belong to the first generation of the lepton particle family,
and are generally thought to be elementary particles because they have no ...
occupying that orbital is likely to be found. Molecular orbitals are approximate solutions to the Schrödinger equation
The Schrödinger equation is a linear partial differential equation that governs the wave function of a quantum-mechanical system. It is a key result in quantum mechanics, and its discovery was a significant landmark in the development of th ...
for the electrons in the electric field of the molecule's atomic nuclei. However calculating the orbitals directly from this equation is far too intractable a problem. Instead they are obtained from the combination of atomic orbitals, which predict the location of an electron in an atom. A molecular orbital can specify the electron configuration of a molecule: the spatial distribution and energy of one (or one pair of) electron(s). Most commonly a MO is represented as a linear combination of atomic orbitals
A linear combination of atomic orbitals or LCAO is a quantum superposition of atomic orbitals and a technique for calculating molecular orbitals in quantum chemistry. In quantum mechanics, electron configurations of atoms are described as wavefun ...
(the LCAO-MO method), especially in qualitative or very approximate usage. They are invaluable in providing a simple model of bonding in molecules, understood through molecular orbital theory.
Most present-day methods in computational chemistry begin by calculating the MOs of the system. A molecular orbital describes the behavior of one electron in the electric field generated by the nuclei and some average distribution of the other electrons. In the case of two electrons occupying the same orbital, the Pauli principle
In quantum mechanics, the Pauli exclusion principle states that two or more identical particles with half-integer spins (i.e. fermions) cannot occupy the same quantum state within a quantum system simultaneously. This principle was formula ...
demands that they have opposite spin. Necessarily this is an approximation, and highly accurate descriptions of the molecular electronic wave function do not have orbitals (see configuration interaction
Configuration interaction (CI) is a post-Hartree–Fock linear variational method for solving the nonrelativistic Schrödinger equation within the Born–Oppenheimer approximation for a quantum chemical multi-electron system. Mathematical ...
).
Molecular orbitals are, in general, delocalized throughout the entire molecule. Moreover, if the molecule has symmetry elements, its nondegenerate molecular orbitals are either symmetric or antisymmetric with respect to any of these symmetries. In other words, application of a symmetry operation S (e.g., a reflection, rotation, or inversion) to molecular orbital ψ results in the molecular orbital being unchanged or reversing its mathematical sign: Sψ = ±ψ. In planar molecules, for example, molecular orbitals are either symmetric ( sigma) or antisymmetric ( pi) with respect to reflection in the molecular plane. If molecules with degenerate orbital energies are also considered, a more general statement that molecular orbitals form bases for the irreducible representations of the molecule's symmetry group holds. The symmetry properties of molecular orbitals means that delocalization is an inherent feature of molecular orbital theory and makes it fundamentally different from (and complementary to) valence bond theory, in which bonds are viewed as localized electron pairs, with allowance for resonance
Resonance describes the phenomenon of increased amplitude that occurs when the frequency of an applied Periodic function, periodic force (or a Fourier analysis, Fourier component of it) is equal or close to a natural frequency of the system ...
to account for delocalization.
In contrast to these symmetry-adapted ''canonical'' molecular orbitals, localized molecular orbitals Localized molecular orbitals are molecular orbitals which are concentrated in a limited spatial region of a molecule, such as a specific bond or lone pair on a specific atom. They can be used to relate molecular orbital calculations to simple bondin ...
can be formed by applying certain mathematical transformations to the canonical orbitals. The advantage of this approach is that the orbitals will correspond more closely to the "bonds" of a molecule as depicted by a Lewis structure. As a disadvantage, the energy levels of these localized orbitals no longer have physical meaning. (The discussion in the rest of this article will focus on canonical molecular orbitals. For further discussions on localized molecular orbitals, see: natural bond orbital and sigma-pi and equivalent-orbital models.)
Formation of molecular orbitals
Molecular orbitals arise from allowed interactions betweenatomic orbital
In atomic theory and quantum mechanics, an atomic orbital is a function describing the location and wave-like behavior of an electron in an atom. This function can be used to calculate the probability of finding any electron of an atom in an ...
s, which are allowed if the symmetries (determined from group theory
In abstract algebra, group theory studies the algebraic structures known as group (mathematics), groups.
The concept of a group is central to abstract algebra: other well-known algebraic structures, such as ring (mathematics), rings, field ...
) of the atomic orbitals are compatible with each other. Efficiency of atomic orbital interactions is determined from the overlap
Overlap may refer to:
* In set theory, an overlap of elements shared between sets is called an intersection, as in a Venn diagram.
* In music theory, overlap is a synonym for reinterpretation of a chord at the boundary of two musical phrases
* O ...
(a measure of how well two orbitals constructively interact with one another) between two atomic orbitals, which is significant if the atomic orbitals are close in energy. Finally, the number of molecular orbitals formed must be equal to the number of atomic orbitals in the atoms being combined to form the molecule.
Qualitative discussion
For an imprecise, but qualitatively useful, discussion of the molecular structure, the molecular orbitals can be obtained from the " Linear combination of atomic orbitals molecular orbital method"ansatz
In physics and mathematics, an ansatz (; , meaning: "initial placement of a tool at a work piece", plural Ansätze ; ) is an educated guess or an additional assumption made to help solve a problem, and which may later be verified to be part of the ...
. Here, the molecular orbitals are expressed as linear combinations of atomic orbital
In atomic theory and quantum mechanics, an atomic orbital is a function describing the location and wave-like behavior of an electron in an atom. This function can be used to calculate the probability of finding any electron of an atom in an ...
s.
Linear combinations of atomic orbitals (LCAO)
Molecular orbitals were first introduced byFriedrich Hund
Friedrich Hermann Hund (4 February 1896 – 31 March 1997) was a German physicist from Karlsruhe known for his work on atoms and molecules.
Scientific career
Hund worked at the Universities of Rostock, Leipzig, Jena, Frankfurt am Main, and Göt ...
and Robert S. Mulliken
Robert Sanderson Mulliken Note Longuet-Higgins' amusing title for reference B238 1965 on page 354 of this Biographical Memoir. The title should be "Selected papers of Robert S Mulliken." (June 7, 1896 – October 31, 1986) was an American ph ...
in 1927 and 1928. The linear combination of atomic orbitals
A linear combination of atomic orbitals or LCAO is a quantum superposition of atomic orbitals and a technique for calculating molecular orbitals in quantum chemistry. In quantum mechanics, electron configurations of atoms are described as wavefun ...
or "LCAO" approximation for molecular orbitals was introduced in 1929 by Sir John Lennard-Jones. His ground-breaking paper showed how to derive the electronic structure of the fluorine and oxygen
Oxygen is the chemical element with the symbol O and atomic number 8. It is a member of the chalcogen group in the periodic table, a highly reactive nonmetal, and an oxidizing agent that readily forms oxides with most elements as ...
molecules from quantum principles. This qualitative approach to molecular orbital theory is part of the start of modern quantum chemistry.
Linear combinations of atomic orbitals (LCAO) can be used to estimate the molecular orbitals that are formed upon bonding between the molecule's constituent atoms. Similar to an atomic orbital, a Schrödinger equation, which describes the behavior of an electron, can be constructed for a molecular orbital as well. Linear combinations of atomic orbitals, or the sums and differences of the atomic wavefunctions, provide approximate solutions to the Hartree–Fock equations which correspond to the independent-particle approximation of the molecular Schrödinger equation
The Schrödinger equation is a linear partial differential equation that governs the wave function of a quantum-mechanical system. It is a key result in quantum mechanics, and its discovery was a significant landmark in the development of th ...
. For simple diatomic molecules, the wavefunctions obtained are represented mathematically by the equations
:
:
where and are the molecular wavefunctions for the bonding and antibonding molecular orbitals, respectively, and are the atomic wavefunctions from atoms a and b, respectively, and and are adjustable coefficients. These coefficients can be positive or negative, depending on the energies and symmetries of the individual atomic orbitals. As the two atoms become closer together, their atomic orbitals overlap to produce areas of high electron density, and, as a consequence, molecular orbitals are formed between the two atoms. The atoms are held together by the electrostatic attraction between the positively charged nuclei and the negatively charged electrons occupying bonding molecular orbitals.
Bonding, antibonding, and nonbonding MOs
When atomic orbitals interact, the resulting molecular orbital can be of three types: bonding, antibonding, or nonbonding. Bonding MOs: * Bonding interactions between atomic orbitals are constructive (in-phase) interactions. * Bonding MOs are lower in energy than the atomic orbitals that combine to produce them. Antibonding MOs: * Antibonding interactions between atomic orbitals are destructive (out-of-phase) interactions, with a nodal plane where the wavefunction of the antibonding orbital is zero between the two interacting atoms * Antibonding MOs are higher in energy than the atomic orbitals that combine to produce them. Nonbonding MOs: * Nonbonding MOs are the result of no interaction between atomic orbitals because of lack of compatible symmetries. * Nonbonding MOs will have the same energy as the atomic orbitals of one of the atoms in the molecule.Sigma and pi labels for MOs
The type of interaction between atomic orbitals can be further categorized by the molecular-orbital symmetry labels σ (sigma), π (pi), δ (delta), φ (phi), γ (gamma) etc. These are the Greek letters corresponding to the atomic orbitals s, p, d, f and g respectively. The number of nodal planes containing the internuclear axis between the atoms concerned is zero for σ MOs, one for π, two for δ, three for φ and four for γ.σ symmetry
A MO with σ symmetry results from the interaction of either two atomic s-orbitals or two atomic pz-orbitals. An MO will have σ-symmetry if the orbital is symmetric with respect to the axis joining the two nuclear centers, the internuclear axis. This means that rotation of the MO about the internuclear axis does not result in a phase change. A σ* orbital, sigma antibonding orbital, also maintains the same phase when rotated about the internuclear axis. The σ* orbital has a nodal plane that is between the nuclei and perpendicular to the internuclear axis.Catherine E. Housecroft, Alan G. Sharpe, ''Inorganic Chemistry'', Pearson Prentice Hall; 2nd Edition, 2005, p. 29-33.π symmetry
A MO with π symmetry results from the interaction of either two atomic px orbitals or py orbitals. An MO will have π symmetry if the orbital is asymmetric with respect to rotation about the internuclear axis. This means that rotation of the MO about the internuclear axis will result in a phase change. There is one nodal plane containing the internuclear axis, if real orbitals are considered. A π* orbital, pi antibonding orbital, will also produce a phase change when rotated about the internuclear axis. The π* orbital also has a second nodal plane between the nuclei.δ symmetry
A MO with δ symmetry results from the interaction of two atomic dxy or dx2-y2 orbitals. Because these molecular orbitals involve low-energy d atomic orbitals, they are seen in transition-metal complexes. A δ bonding orbital has two nodal planes containing the internuclear axis, and a δ* antibonding orbital also has a third nodal plane between the nuclei.φ symmetry
Theoretical chemists have conjectured that higher-order bonds, such as phi bonds corresponding to overlap of f atomic orbitals, are possible. There is no known example of a molecule purported to contain a phi bond.Gerade and ungerade symmetry
For molecules that possess a center of inversion ( centrosymmetric molecules) there are additional labels of symmetry that can be applied to molecular orbitals. Centrosymmetric molecules include: *Homonuclear
Homonuclear molecules, or homonuclear species, are molecules composed of only one element. Homonuclear molecules may consist of various numbers of atoms. The size of the molecule an element can form depends on the element's properties, and some el ...
diatomics, X2
* Octahedral
In geometry, an octahedron (plural: octahedra, octahedrons) is a polyhedron with eight faces. The term is most commonly used to refer to the regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet a ...
, EX6
* Square planar, EX4.
Non-centrosymmetric molecules include:
* Heteronuclear diatomics, XY
* Tetrahedral
In geometry, a tetrahedron (plural: tetrahedra or tetrahedrons), also known as a triangular pyramid, is a polyhedron composed of four triangular faces, six straight edges, and four vertex corners. The tetrahedron is the simplest of all the ...
, EX4.
If inversion through the center of symmetry in a molecule results in the same phases for the molecular orbital, then the MO is said to have gerade (g) symmetry, from the German word for even.
If inversion through the center of symmetry in a molecule results in a phase change for the molecular orbital, then the MO is said to have ungerade (u) symmetry, from the German word for odd.
For a bonding MO with σ-symmetry, the orbital is σg (s' + sMO diagrams
The qualitative approach of MO analysis uses a molecular orbital diagram to visualize bonding interactions in a molecule. In this type of diagram, the molecular orbitals are represented by horizontal lines; the higher a line the higher the energy of the orbital, and degenerate orbitals are placed on the same level with a space between them. Then, the electrons to be placed in the molecular orbitals are slotted in one by one, keeping in mind the Pauli exclusion principle and Hund's rule of maximum multiplicity (only 2 electrons, having opposite spins, per orbital; place as many unpaired electrons on one energy level as possible before starting to pair them). For more complicated molecules, the wave mechanics approach loses utility in a qualitative understanding of bonding (although is still necessary for a quantitative approach). Some properties: * A basis set of orbitals includes those atomic orbitals that are available for molecular orbital interactions, which may be bonding or antibonding * The number of molecular orbitals is equal to the number of atomic orbitals included in the linear expansion or the basis set * If the molecule has some symmetry, the degenerate atomic orbitals (with the same atomic energy) are grouped in linear combinations (called symmetry-adapted atomic orbitals (SO)), which belong to the representation of the symmetry group, so thewave function
A wave function in quantum physics is a mathematical description of the quantum state of an isolated quantum system. The wave function is a complex-valued probability amplitude, and the probabilities for the possible results of measurements ...
s that describe the group are known as symmetry-adapted linear combinations (SALC).
* The number of molecular orbitals belonging to one group representation is equal to the number of symmetry-adapted atomic orbitals belonging to this representation
* Within a particular representation, the symmetry-adapted atomic orbitals mix more if their atomic energy level
A quantum mechanical system or particle that is bound—that is, confined spatially—can only take on certain discrete values of energy, called energy levels. This contrasts with classical particles, which can have any amount of energy. The t ...
s are closer.
The general procedure for constructing a molecular orbital diagram for a reasonably simple molecule can be summarized as follows:
1. Assign a point group to the molecule.
2. Look up the shapes of the SALCs.
3. Arrange the SALCs of each molecular fragment in increasing order of energy, first noting whether they stem from ''s'', ''p'', or ''d'' orbitals
(and put them in the order ''s'' < ''p'' < ''d''), and then their number of internuclear nodes.
4. Combine SALCs of the same symmetry type from the two fragments, and from N SALCs form N molecular orbitals.
5. Estimate the relative energies of the molecular orbitals from considerations of overlap and relative energies of the parent orbitals, and draw the levels on a molecular orbital energy level diagram (showing the origin of the orbitals).
6. Confirm, correct, and revise this qualitative order by carrying out a molecular orbital calculation by using commercial software.
Bonding in molecular orbitals
Orbital degeneracy
Molecular orbitals are said to be degenerate if they have the same energy. For example, in the homonuclear diatomic molecules of the first ten elements, the molecular orbitals derived from the px and the py atomic orbitals result in two degenerate bonding orbitals (of low energy) and two degenerate antibonding orbitals (of high energy).Ionic bonds
When the energy difference between the atomic orbitals of two atoms is quite large, one atom's orbitals contribute almost entirely to the bonding orbitals, and the other atom's orbitals contribute almost entirely to the antibonding orbitals. Thus, the situation is effectively that one or more electrons have been transferred from one atom to the other. This is called an (mostly)ionic bond
Ionic bonding is a type of chemical bonding that involves the electrostatic attraction between oppositely charged ions, or between two atoms with sharply different electronegativities, and is the primary interaction occurring in ionic compounds ...
.
Bond order
The bond order, or number of bonds, of a molecule can be determined by combining the number of electrons in bonding and antibonding molecular orbitals. A pair of electrons in a bonding orbital creates a bond, whereas a pair of electrons in an antibonding orbital negates a bond. For example, N2, with eight electrons in bonding orbitals and two electrons in antibonding orbitals, has a bond order of three, which constitutes a triple bond.Bond strength
In chemistry, bond energy (''BE''), also called the mean bond enthalpy or average bond enthalpy is the measure of bond strength in a chemical bond. IUPAC defines bond energy as the average value of the gas-phase bond-dissociation energy (usually at ...
is proportional to bond order—a greater amount of bonding produces a more stable bond—and bond length
In molecular geometry, bond length or bond distance is defined as the average distance between nuclei of two bonded atoms in a molecule. It is a transferable property of a bond between atoms of fixed types, relatively independent of the rest of ...
is inversely proportional to it—a stronger bond is shorter.
There are rare exceptions to the requirement of molecule having a positive bond order. Although Be2 has a bond order of 0 according to MO analysis, there is experimental evidence of a highly unstable Be2 molecule having a bond length of 245 pm and bond energy of 10 kJ/mol.
HOMO and LUMO
The highest occupied molecular orbital and lowest unoccupied molecular orbital are often referred to as the HOMO and LUMO, respectively. The difference of the energies of the HOMO and LUMO is called the HOMO-LUMO gap. This notion is often the matter of confusion in literature and should be considered with caution. Its value is usually located between the fundamental gap (difference between ionization potential and electron affinity) and the optical gap. In addition, HOMO-LUMO gap can be related to a bulk materialband gap
In solid-state physics, a band gap, also called an energy gap, is an energy range in a solid where no electronic states can exist. In graphs of the electronic band structure of solids, the band gap generally refers to the energy difference ( ...
or transport gap, which is usually much smaller than fundamental gap.
Examples
Homonuclear diatomics
Homonuclear diatomic MOs contain equal contributions from each atomic orbital in the basis set. This is shown in the homonuclear diatomic MO diagrams for H2, He2, and Li2, all of which containing symmetric orbitals.H2
 As a simple MO example, consider the electrons in a
As a simple MO example, consider the electrons in a hydrogen
Hydrogen is the chemical element with the symbol H and atomic number 1. Hydrogen is the lightest element. At standard conditions hydrogen is a gas of diatomic molecules having the formula . It is colorless, odorless, tasteless, non-toxic ...
molecule, H2 (see molecular orbital diagram
A molecular orbital diagram, or MO diagram, is a qualitative descriptive tool explaining chemical bonding in molecules in terms of molecular orbital theory in general and the linear combination of atomic orbitals (LCAO) method in particular. A f ...
), with the two atoms labelled H' and H". The lowest-energy atomic orbitals, 1s' and 1s", do not transform according to the symmetries of the molecule. However, the following symmetry adapted atomic orbitals do:
The symmetric combination (called a bonding orbital) is lower in energy than the basis orbitals, and the antisymmetric combination (called an antibonding orbital) is higher. Because the H2 molecule has two electrons, they can both go in the bonding orbital, making the system lower in energy (hence more stable) than two free hydrogen atoms. This is called a covalent bond. The bond order is equal to the number of bonding electrons minus the number of antibonding electrons, divided by 2. In this example, there are 2 electrons in the bonding orbital and none in the antibonding orbital; the bond order is 1, and there is a single bond between the two hydrogen atoms.
He2
On the other hand, consider the hypothetical molecule of He2 with the atoms labeled He' and He". As with H2, the lowest energy atomic orbitals are the 1s' and 1s", and do not transform according to the symmetries of the molecule, while the symmetry adapted atomic orbitals do. The symmetric combination—the bonding orbital—is lower in energy than the basis orbitals, and the antisymmetric combination—the antibonding orbital—is higher. Unlike H2, with two valence electrons, He2 has four in its neutral ground state. Two electrons fill the lower-energy bonding orbital, σg(1s), while the remaining two fill the higher-energy antibonding orbital, σu*(1s). Thus, the resulting electron density around the molecule does not support the formation of a bond between the two atoms; without a stable bond holding the atoms together, the molecule would not be expected to exist. Another way of looking at it is that there are two bonding electrons and two antibonding electrons; therefore, the bond order is 0 and no bond exists (the molecule has one bound state supported by the Van der Waals potential).Li2
Dilithium Li2 is formed from the overlap of the 1s and 2s atomic orbitals (the basis set) of two Li atoms. Each Li atom contributes three electrons for bonding interactions, and the six electrons fill the three MOs of lowest energy, σg(1s), σu*(1s), and σg(2s). Using the equation for bond order, it is found that dilithium has a bond order of one, a single bond.Noble gases
Considering a hypothetical molecule of He2, since the basis set of atomic orbitals is the same as in the case of H2, we find that both the bonding and antibonding orbitals are filled, so there is no energy advantage to the pair. HeH would have a slight energy advantage, but not as much as H2 + 2 He, so the molecule is very unstable and exists only briefly before decomposing into hydrogen and helium. In general, we find that atoms such as He that have full energy shells rarely bond with other atoms. Except for short-lived Van der Waals complexes, there are very fewnoble gas compound
In chemistry, noble gas compounds are chemical compounds that include an element from the noble gases, group 18 of the periodic table. Although the noble gases are generally unreactive elements, many such compounds have been observed, particularl ...
s known.
Heteronuclear diatomics
While MOs for homonuclear diatomic molecules contain equal contributions from each interacting atomic orbital, MOs for heteronuclear diatomics contain different atomic orbital contributions. Orbital interactions to produce bonding or antibonding orbitals in heteronuclear diatomics occur if there is sufficient overlap between atomic orbitals as determined by their symmetries and similarity in orbital energies.HF
In hydrogen fluoride HF overlap between the H 1s and F 2s orbitals is allowed by symmetry but the difference in energy between the two atomic orbitals prevents them from interacting to create a molecular orbital. Overlap between the H 1s and F 2pz orbitals is also symmetry allowed, and these two atomic orbitals have a small energy separation. Thus, they interact, leading to creation of σ and σ* MOs and a molecule with a bond order of 1. Since HF is a non-centrosymmetric molecule, the symmetry labels g and u do not apply to its molecular orbitals.Catherine E. Housecroft, Alan G, Sharpe, Inorganic Chemistry, Pearson Prentice Hall; 2nd Edition, 2005, , p. 41-43.Quantitative approach
To obtain quantitative values for the molecularenergy level
A quantum mechanical system or particle that is bound—that is, confined spatially—can only take on certain discrete values of energy, called energy levels. This contrasts with classical particles, which can have any amount of energy. The t ...
s, one needs to have molecular orbitals that are such that the configuration interaction
Configuration interaction (CI) is a post-Hartree–Fock linear variational method for solving the nonrelativistic Schrödinger equation within the Born–Oppenheimer approximation for a quantum chemical multi-electron system. Mathematical ...
(CI) expansion converges fast towards the full CI limit. The most common method to obtain such functions is the Hartree–Fock method
In computational physics and chemistry, the Hartree–Fock (HF) method is a method of approximation for the determination of the wave function and the energy of a quantum many-body system in a stationary state.
The Hartree–Fock method often ...
, which expresses the molecular orbitals as eigenfunction
In mathematics, an eigenfunction of a linear operator ''D'' defined on some function space is any non-zero function f in that space that, when acted upon by ''D'', is only multiplied by some scaling factor called an eigenvalue. As an equation, th ...
s of the Fock operator. One usually solves this problem by expanding the molecular orbitals as linear combinations of Gaussian function
In mathematics, a Gaussian function, often simply referred to as a Gaussian, is a function of the base form
f(x) = \exp (-x^2)
and with parametric extension
f(x) = a \exp\left( -\frac \right)
for arbitrary real constants , and non-zero . It is ...
s centered on the atomic nuclei (see linear combination of atomic orbitals
A linear combination of atomic orbitals or LCAO is a quantum superposition of atomic orbitals and a technique for calculating molecular orbitals in quantum chemistry. In quantum mechanics, electron configurations of atoms are described as wavefun ...
and basis set (chemistry)). The equation for the coefficients of these linear combinations is a generalized eigenvalue equation known as the Roothaan equations, which are in fact a particular representation of the Hartree–Fock equation. There are a number of programs in which quantum chemical calculations of MOs can be performed, including Spartan
Sparta ( Doric Greek: Σπάρτα, ''Spártā''; Attic Greek: Σπάρτη, ''Spártē'') was a prominent city-state in Laconia, in ancient Greece. In antiquity, the city-state was known as Lacedaemon (, ), while the name Sparta refe ...
.
Simple accounts often suggest that experimental molecular orbital energies can be obtained by the methods of ultra-violet photoelectron spectroscopy for valence orbitals and X-ray photoelectron spectroscopy
X-ray photoelectron spectroscopy (XPS) is a surface-sensitive quantitative spectroscopic technique based on the photoelectric effect that can identify the elements that exist within a material (elemental composition) or are covering its surface, ...
for core orbitals. This, however, is incorrect as these experiments measure the ionization energy, the difference in energy between the molecule and one of the ions resulting from the removal of one electron. Ionization energies are linked approximately to orbital energies by Koopmans' theorem. While the agreement between these two values can be close for some molecules, it can be very poor in other cases.
Notes
References
{{Authority control Molecular physics Quantum chemistry Theoretical chemistry Computational chemistry Chemical bonding