Law of the iterated logarithm

In probability theory, the law of the iterated logarithm describes the magnitude of the fluctuations of a random walk. The original statement of the law of the iterated logarithm is due to A. Ya. Khinchin (1924). Another statement was given by A. N. Kolmogorov in 1929.

Statement

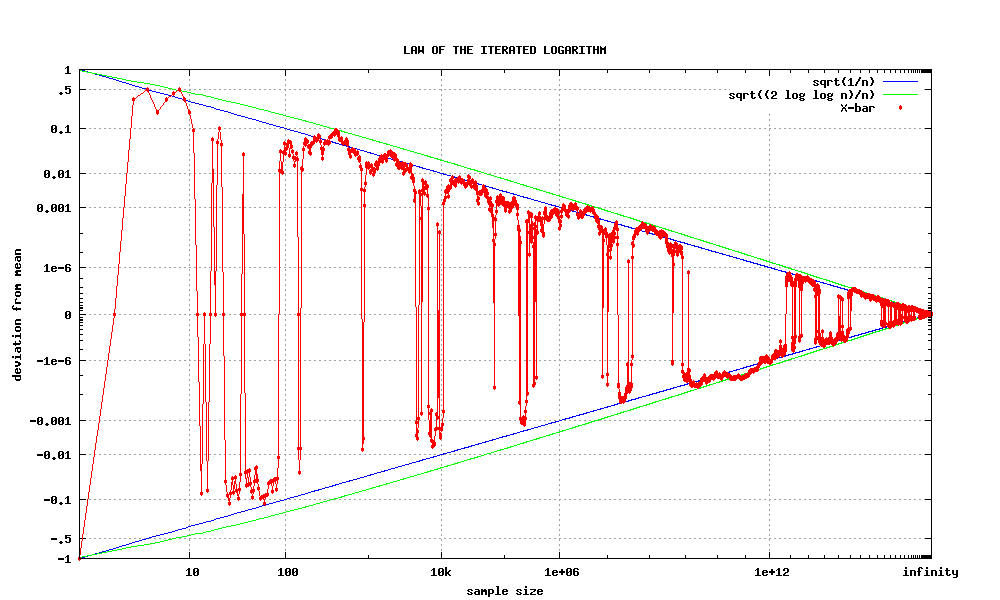
Let be independent, identically distributed random variables with means zero and unit variances. Let ''S''_''n'' = ''Y''₁ + ... + ''Y''_''n''. Then
: $\limsup_ \frac = 1 \quad \text,$
where “log” is the natural logarithm, “lim sup” denotes the limit superior, and “a.s.” stands for “almost surely”.

Discussion

The law of iterated logarithms operates “in between” the law of large numbers and the central limit theorem. There are two versions of the law of large numbers — the weak and the strong — and they both state that the sums ''S''_''n'', scaled by ''n''⁻¹, converge to zero, respectively in probability and almost surely:
: $\frac \ \xrightarrow\ 0, \qquad \frac \ \xrightarrow 0, \qquad \text\ \ n\to\infty.$

On the other hand, the central limit theorem states that the sums ''S''_''n'' scaled by the factor ''n''^−½ converge in distribution to a standard normal distribution. By Kolmogorov's zero–one law, for any fixed ''M'', the probability that the event
$\limsup_n \frac \geq M$
occurs is 0 or 1.
Then

: $\Pr\left( \limsup_n \frac \geq M \right) \geqslant \limsup_n \Pr\left( \frac \geq M \right) = \Pr\left( \mathcal(0, 1) \geq M \right) > 0$

so

:$\limsup_n \frac=\infty \qquad \text$

An identical argument shows that

:$\liminf_n \frac=-\infty \qquad \text$

This implies that these quantities cannot converge almost surely. In fact, they cannot even converge in probability, which follows from the equality

:$\frac-\frac = \frac1\frac - \left (1-\frac1\sqrt2 \right )\frac$

and the fact that the random variables

:$\frac\quad \text \quad \frac$

are independent and both converge in distribution to $\mathcal(0, 1).$

The ''law of the iterated logarithm'' provides the scaling factor where the two limits become different:
: $\frac \ \xrightarrow\ 0, \qquad \frac \ \stackrel\ 0, \qquad \text\ \ n\to\infty.$

Thus, although the absolute value of the quantity $S_n/\sqrt$ is less than any predefined ''ε'' > 0 with probability approaching one, it will nevertheless almost surely be greater than ''ε'' infinitely often; in fact, the quantity will be visiting the neighborhoods of any point in the interval (-1,1) almost surely.

Generalizations and variants

The law of the iterated logarithm (LIL) for a sum of independent and identically distributed (i.i.d.) random variables with zero mean and bounded increment dates back to Khinchin and Kolmogorov in the 1920s.

Since then, there has been a tremendous amount of work on the LIL for various kinds of
dependent structures and for stochastic processes. The following is a small sample of notable developments.

Hartman–Wintner (1940) generalized LIL to random walks with increments with zero mean and finite variance. De Acosta (1983) gave a simple proof of the Hartman–Wintner version of the LIL.

Strassen (1964) studied the LIL from the point of view of invariance principles.

Stout (1970) generalized the LIL to stationary ergodic martingales.

Wittmann (1985) generalized Hartman–Wintner version of LIL to random walks satisfying milder conditions.

Vovk (1987) derived a version of LIL valid for a single chaotic sequence (Kolmogorov random sequence). This is notable, as it is outside the realm of classical probability theory.

Yongge Wang (1996) showed that the law of the iterated logarithm holds for polynomial time pseudorandom sequences also. The Java-based softwar
testing tool
tests whether a pseudorandom generator outputs sequences that satisfy the LIL.

Balsubramani (2014) proved a non-asymptotic LIL that holds over finite-time martingale sample paths. This subsumes the martingale LIL as it provides matching finite-sample concentration and anti-concentration bounds, and enables sequential testing and other applications.C. Daskalakis and Y. Kawase:
Optimal Stopping Rules for Sequential Hypothesis Testing
. In 25th Annual European Symposium on Algorithms (ESA 2017). Schloss Dagstuhl-Leibniz-Zentrum fuer Informatik.

See also

* Iterated logarithm
* Brownian motion

Notes

{{reflist

Asymptotic theory (statistics)
Theorems in statistics
Stochastic processes