Kepler–Poinsot polyhedron

In geometry, a Kepler–Poinsot polyhedron is any of four regular star polyhedra.

They may be obtained by stellating the regular convex dodecahedron and icosahedron, and differ from these in having regular pentagrammic faces or vertex figures. They can all be seen as three-dimensional analogues of the pentagram in one way or another.

Characteristics

Non-convexity

These figures have pentagrams (star pentagons) as faces or vertex figures. The small and great stellated dodecahedron have nonconvex regular pentagram faces. The great dodecahedron and great icosahedron have convex polygonal faces, but pentagrammic vertex figures.

In all cases, two faces can intersect along a line that is not an edge of either face, so that part of each face passes through the interior of the figure. Such lines of intersection are not part of the polyhedral structure and are sometimes called false edges. Likewise where three such lines intersect at a point that is not a corner of any face, these points are false vertices. The images below show spheres at the true vertices, and blue rods along the true edges.

For example, the small stellated dodecahedron has 12 pentagram faces with the central pentagonal part hidden inside the solid. The visible parts of each face comprise five isosceles triangles which touch at five points around the pentagon. We could treat these triangles as 60 separate faces to obtain a new, irregular polyhedron which looks outwardly identical. Each edge would now be divided into three shorter edges (of two different kinds), and the 20 false vertices would become true ones, so that we have a total of 32 vertices (again of two kinds). The hidden inner pentagons are no longer part of the polyhedral surface, and can disappear. Now Euler's formula holds: 60 − 90 + 32 = 2. However, this polyhedron is no longer the one described by the Schläfli symbol , and so can not be a Kepler–Poinsot solid even though it still looks like one from outside.

Euler characteristic χ

A Kepler–Poinsot polyhedron covers its circumscribed sphere more than once, with the centers of faces acting as winding points in the figures which have pentagrammic faces, and the vertices in the others. Because of this, they are not necessarily topologically equivalent to the sphere as Platonic solids are, and in particular the Euler relation

:$\chi=V-E+F=2\$

does not always hold. Schläfli held that all polyhedra must have χ = 2, and he rejected the small stellated dodecahedron and great dodecahedron as proper polyhedra. This view was never widely held.

A modified form of Euler's formula, using density (''D'') of the vertex figures ($d_v$) and faces ($d_f$) was given by Arthur Cayley, and holds both for convex polyhedra (where the correction factors are all 1), and the Kepler–Poinsot polyhedra:
:$d_v V - E + d_f F = 2D.$

Duality and Petrie polygons

The Kepler–Poinsot polyhedra exist in dual pairs. Duals have the same Petrie polygon, or more precisely, Petrie polygons with the same two dimensional projection.

The following images show the two dual compounds with the same edge radius. They also show that the Petrie polygons are skew.
Two relationships described in the article below are also easily seen in the images: That the violet edges are the same, and that the green faces lie in the same planes.

Summary

Relationships among the regular polyhedra

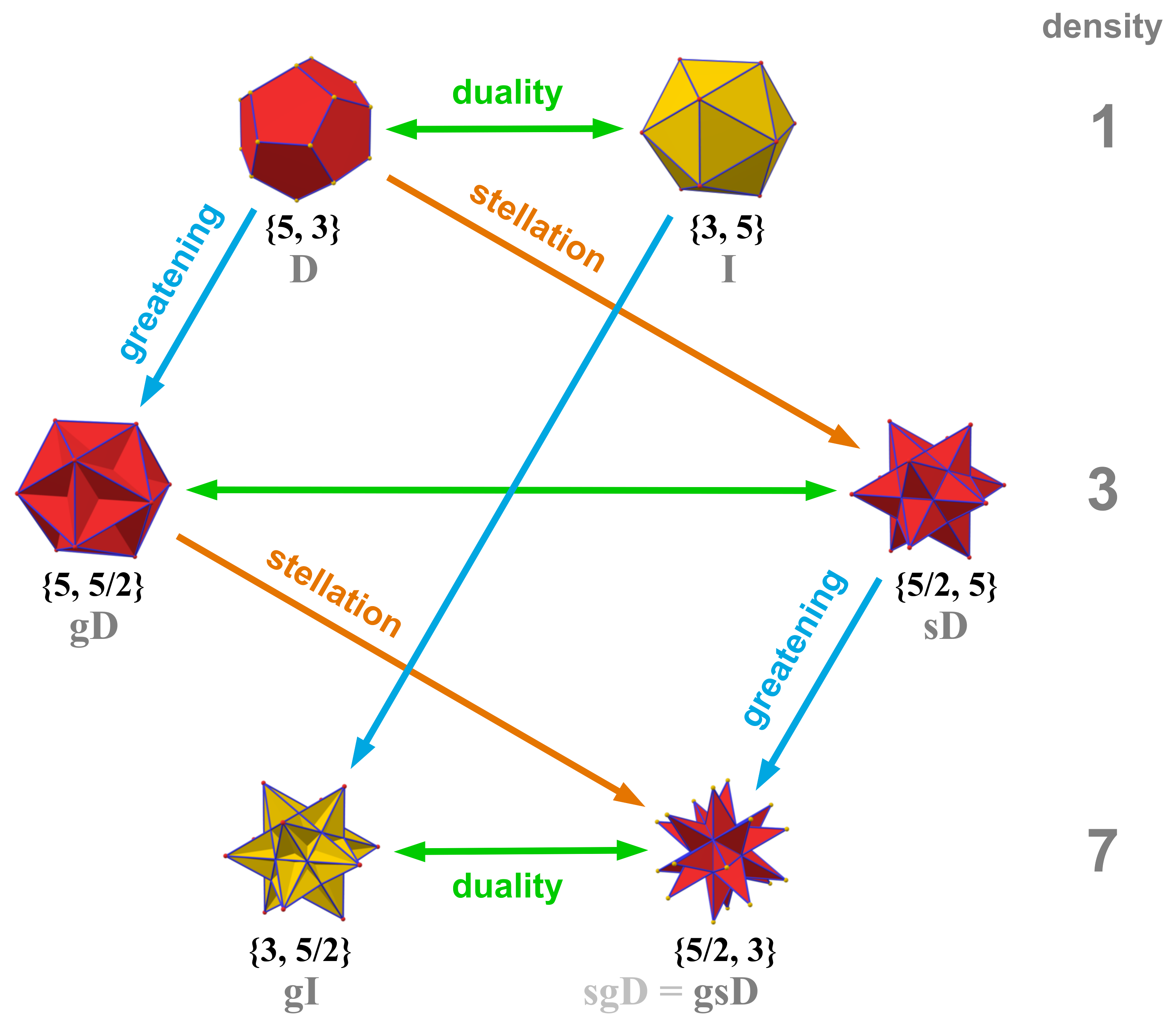
Conway's operational terminology

John Conway defines the Kepler–Poinsot polyhedra as ''greatenings'' and ''stellations'' of the convex solids.

In his naming convention the small stellated dodecahedron is just the ''stellated dodecahedron''.

''Stellation'' changes pentagonal faces into pentagrams. (In this sense stellation is a unique operation, and not to be confused with the more general stellation described below.)

''Greatening'' maintains the type of faces, shifting and resizing them into parallel planes.

Stellations and facetings

The great icosahedron is one of the stellations of the icosahedron. (See The Fifty-Nine Icosahedra)

The three others are all the stellations of the dodecahedron.

The great stellated dodecahedron is a faceting of the dodecahedron.

The three others are facetings of the icosahedron.

If the intersections are treated as new edges and vertices, the figures obtained will not be regular, but they can still be considered stellations.

(See also List of Wenninger polyhedron models)

Shared vertices and edges

The great stellated dodecahedron shares its vertices with the dodecahedron. The other three Kepler–Poinsot polyhedra share theirs with the icosahedron.

The stellated dodecahedra

Hull and core

The small and great stellated dodecahedron
can be seen as a regular and a great dodecahedron with their edges and faces extended until they intersect.

The pentagon faces of these cores are the invisible parts of the star polyhedra's pentagram faces.

For the small stellated dodecahedron the hull is $\varphi$ times bigger than the core, and for the great it is $\varphi + 1 = \varphi^2$ times bigger.


(The midradius is a common measure to compare the size of different polyhedra.)

Augmentations

Traditionally the two star polyhedra have been defined as ''augmentations'' (or ''cumulations''),

Kepler calls the small stellation an ''augmented dodecahedron'' (then nicknaming it ''hedgehog'').

These naïve definitions are still used.
E.g. MathWorld states that the two star polyhedra can be constructed by adding pyramids to the faces of the Platonic solids.

Symmetry

All Kepler–Poinsot polyhedra have full icosahedral symmetry, just like their convex hulls.

The great icosahedron and its dual resemble the icosahedron and its dual in that they have faces and vertices on the 3-fold (yellow) and 5-fold (red) symmetry axes.

In the great dodecahedron and its dual all faces and vertices are on 5-fold symmetry axes (so there are no yellow elements in these images).

The following table shows the solids in pairs of duals. In the top row they are shown with pyritohedral symmetry, in the bottom row with icosahedral symmetry (to which the mentioned colors refer).

The table below shows orthographic projections from the 5-fold (red), 3-fold (yellow) and 2-fold (blue) symmetry axes.

History

Most, if not all, of the Kepler-Poinsot polyhedra were known of in some form or other before Kepler. A small stellated dodecahedron appears in a marble tarsia (inlay panel) on the floor of St. Mark's Basilica, Venice, Italy. It dates from the 15th century and is sometimes attributed to Paolo Uccello.

In his ''Perspectiva corporum regularium'' (''Perspectives of the regular solids''), a book of woodcuts published in 1568, Wenzel Jamnitzer depicts the great stellated dodecahedron and a great dodecahedron (both shown below). There is also a truncated version of the small stellated dodecahedron. It is clear from the general arrangement of the book that he regarded only the five Platonic solids as regular.

The small and great stellated dodecahedra, sometimes called the Kepler polyhedra, were first recognized as regular by Johannes Kepler around 1619.H.S.M. Coxeter,P. Du Val, H.T. Flather and J.F. Petrie; ''The Fifty-Nine Icosahedra'', 3rd Edition, Tarquin, 1999. p.11 He obtained them by stellating the regular convex dodecahedron, for the first time treating it as a surface rather than a solid. He noticed that by extending the edges or faces of the convex dodecahedron until they met again, he could obtain star pentagons. Further, he recognized that these star pentagons are also regular. In this way he constructed the two stellated dodecahedra. Each has the central convex region of each face "hidden" within the interior, with only the triangular arms visible. Kepler's final step was to recognize that these polyhedra fit the definition of regularity, even though they were not convex, as the traditional Platonic solids were.

In 1809, Louis Poinsot rediscovered Kepler's figures, by assembling star pentagons around each vertex. He also assembled convex polygons around star vertices to discover two more regular stars, the great icosahedron and great dodecahedron. Some people call these two the Poinsot polyhedra. Poinsot did not know if he had discovered all the regular star polyhedra.

Three years later, Augustin Cauchy proved the list complete by stellating the Platonic solids, and almost half a century after that, in 1858, Bertrand provided a more elegant proof by faceting them.

The following year, Arthur Cayley gave the Kepler–Poinsot polyhedra the names by which they are generally known today.

A hundred years later, John Conway developed a systematic terminology for stellations in up to four dimensions. Within this scheme the small stellated dodecahedron is just the ''stellated dodecahedron''.

Regular star polyhedra in art and culture

A dissection of the great dodecahedron was used for the 1980s puzzle Alexander's Star.
Regular star polyhedra first appear in Renaissance art. A small stellated dodecahedron is depicted in a marble tarsia on the floor of St. Mark's Basilica, Venice, Italy, dating from ca. 1430 and sometimes attributed to Paulo Ucello.

In the 20th Century, Artist M. C. Escher's interest in geometric forms often led to works based on or including regular solids; ''Gravitation'' is based on a small stellated dodecahedron.

Norwegian artist Vebjørn Sand's sculpture ''The Kepler Star'' is displayed near Oslo Airport, Gardermoen. The star spans 14 meters, and consists of an icosahedron and a dodecahedron inside a great stellated dodecahedron.

See also

* Regular polytope
* Regular polyhedron
* List of regular polytopes
* Uniform polyhedron
* Uniform star polyhedron
* Polyhedral compound
* Regular star 4-polytope – the ten regular star 4-polytopes, 4-dimensional analogues of the Kepler–Poinsot polyhedra

References

Notes

Bibliography

* J. Bertrand, Note sur la théorie des polyèdres réguliers, ''Comptes rendus des séances de l'Académie des Sciences'', 46 (1858), pp. 79–82, 117.
* Augustin-Louis Cauchy, ''Recherches sur les polyèdres.'' J. de l'École Polytechnique 9, 68–86, 1813.
* Arthur Cayley, On Poinsot's Four New Regular Solids. ''Phil. Mag.'' 17, pp. 123–127 and 209, 1859.
* John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, ''The Symmetry of Things'' 2008, (Chapter 24, Regular Star-polytopes, pp. 404–408)
* ''Kaleidoscopes: Selected Writings of H. S. M. Coxeter'', edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995,

** (Paper 1) H.S.M. Coxeter, ''The Nine Regular Solids'' roc. Can. Math. Congress 1 (1947), 252–264, MR 8, 482** (Paper 10) H.S.M. Coxeter, ''Star Polytopes and the Schlafli Function f(α,β,γ)'' lemente der Mathematik 44 (2) (1989) 25–36* Theoni Pappas, (The Kepler–Poinsot Solids) ''The Joy of Mathematics''. San Carlos, CA: Wide World Publ./Tetra, p. 113, 1989.
* Louis Poinsot, Memoire sur les polygones et polyèdres. ''J. de l'École Polytechnique'' 9, pp. 16–48, 1810.
* Lakatos, Imre; ''Proofs and Refutations'', Cambridge University Press (1976) - discussion of proof of Euler characteristic
* , pp. 39–41.
* John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, ''The Symmetries of Things'' 2008, (Chapter 26. pp. 404: Regular star-polytopes Dimension 3)
* Chapter 8: Kepler Poisot polyhedra

External links

*
Paper models of Kepler–Poinsot polyhedraFree paper models (nets) of Kepler–Poinsot polyhedraThe Uniform Polyhedra
in Visual Polyhedra
Stella: Polyhedron Navigator
Software used to create many of the images on this page.

{{DEFAULTSORT:Kepler-Poinsot Polyhedron

Johannes Kepler
Nonconvex polyhedra