Halbach array on:
[Wikipedia]
[Google]
[Amazon]


 A Halbach array is a special arrangement of permanent
A Halbach array is a special arrangement of permanent
 Although this magnetic flux distribution seems somewhat counter-intuitive to those familiar with simple bar magnets or solenoids, the reason for this flux distribution can be intuitively visualised using Mallinson's original diagram (note that it uses the negative ''y'' component, unlike the diagram in Mallinson's article). The diagram shows the field from a strip of ferromagnetic material with alternating magnetization in the ''y'' direction (top left) and in the ''x'' direction (top right). Note that the field above the plane is in the ''same'' direction for both structures, but the field below the plane is in ''opposite'' directions. The effect of superimposing both of these structures is shown in the figure.
The crucial point is that the flux will ''cancel below the plane and reinforce itself above the plane''. In fact, any magnetization pattern where the components of magnetization are out of phase with each other will result in a one-sided flux. The mathematical transform that shifts the phase of all components of some function by is called a Hilbert transform; the components of the magnetization vector can therefore be any Hilbert-transform pair (the simplest of which is simply , as shown in the diagram above).
Although this magnetic flux distribution seems somewhat counter-intuitive to those familiar with simple bar magnets or solenoids, the reason for this flux distribution can be intuitively visualised using Mallinson's original diagram (note that it uses the negative ''y'' component, unlike the diagram in Mallinson's article). The diagram shows the field from a strip of ferromagnetic material with alternating magnetization in the ''y'' direction (top left) and in the ''x'' direction (top right). Note that the field above the plane is in the ''same'' direction for both structures, but the field below the plane is in ''opposite'' directions. The effect of superimposing both of these structures is shown in the figure.
The crucial point is that the flux will ''cancel below the plane and reinforce itself above the plane''. In fact, any magnetization pattern where the components of magnetization are out of phase with each other will result in a one-sided flux. The mathematical transform that shifts the phase of all components of some function by is called a Hilbert transform; the components of the magnetization vector can therefore be any Hilbert-transform pair (the simplest of which is simply , as shown in the diagram above).
 The field on the non-cancelling side of the ideal, continuously varying, infinite array is of the form
:
where
: is the field in the form ,
: is the magnitude of the field at the surface of the array,
: is the
The field on the non-cancelling side of the ideal, continuously varying, infinite array is of the form
:
where
: is the field in the form ,
: is the magnitude of the field at the surface of the array,
: is the
 The simplest example of a one-sided flux magnet is a refrigerator magnet. These are usually composed of powdered ferrite in a binder such as plastic or rubber. The
The simplest example of a one-sided flux magnet is a refrigerator magnet. These are usually composed of powdered ferrite in a binder such as plastic or rubber. The  Scaling up this design and adding a top sheet gives a wiggler magnet, used in
Scaling up this design and adding a top sheet gives a wiggler magnet, used in

 A series of magnetic rods, magnetized perpendicular to their axes, can be arranged into a Halbach array. If each rod is then rotated alternately through 90°, the resultant field moves from one side of plane of the rods to the other, as shown schematically in the figure.
This arrangement allows the field to effectively be turned on and off above or below the plane of the rods, depending on the rotation of the rods. Such a device makes an efficient mechanical magnetic latch requiring no power. A detailed study of this arrangement has shown that each rod is subject to a strong torque from its neighboring rods, and therefore requires mechanical stabilization. However, a simple and efficient solution, providing both stabilization and the ability to rotate each rod alternately, is simply to provide an equal-gearing arrangement on each rod, as shown in the figure.
A series of magnetic rods, magnetized perpendicular to their axes, can be arranged into a Halbach array. If each rod is then rotated alternately through 90°, the resultant field moves from one side of plane of the rods to the other, as shown schematically in the figure.
This arrangement allows the field to effectively be turned on and off above or below the plane of the rods, depending on the rotation of the rods. Such a device makes an efficient mechanical magnetic latch requiring no power. A detailed study of this arrangement has shown that each rod is subject to a strong torque from its neighboring rods, and therefore requires mechanical stabilization. However, a simple and efficient solution, providing both stabilization and the ability to rotate each rod alternately, is simply to provide an equal-gearing arrangement on each rod, as shown in the figure.

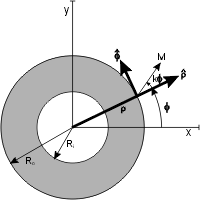 A Halbach cylinder is a magnetized cylinder composed of
A Halbach cylinder is a magnetized cylinder composed of
 For the special case of ''k'' = 2, the field inside the bore is uniform and is given by
:
where the inner and outer cylinder radii are ''R''i and ''R''o respectively. ''H'' is in the ''y'' direction. This is the simplest form of the Halbach cylinder, and it can be seen that if the ratio of outer to inner radii is greater than ''e'', the flux inside the bore actually exceeds the
For the special case of ''k'' = 2, the field inside the bore is uniform and is given by
:
where the inner and outer cylinder radii are ''R''i and ''R''o respectively. ''H'' is in the ''y'' direction. This is the simplest form of the Halbach cylinder, and it can be seen that if the ratio of outer to inner radii is greater than ''e'', the flux inside the bore actually exceeds the 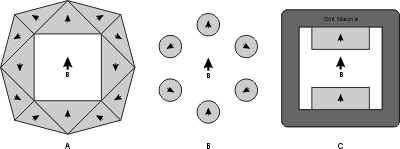 This cylindrical design is only one class of designs that produce a uniform field inside a cavity within an array of permanent magnets. Other classes of design include wedge designs, proposed by Abele and Jensen, in which wedges of magnetized material are arranged to provide uniform field within cavities inside the design as shown.
The direction of magnetization of the wedges in (A) can be calculated using a set of rules given by Abele and allows for great freedom in the shape of the cavity. Another class of design is the magnetic mangle (B), proposed by Coey and Cugat, in which uniformly magnetized rods are arranged such that their magnetization matches that of a Halbach cylinder, as shown for a 6-rod design. This design greatly increases access to the region of uniform field, at the expense of the volume of uniform field being smaller than in the cylindrical designs (although this area can be made larger by increasing the number of component rods). Rotating the rods relative to each other results in many possibilities, including a dynamically variable field and various dipolar configurations. It can be seen that the designs shown in (A) and (B) are closely related to the ''k'' = 2 Halbach cylinder. Other very simple designs for a uniform field include separated magnets with soft iron return paths, as shown in figure (C).
In recent years, these Halbach dipoles have been used to conduct low-field NMR experiments. Compared to commercially available ( Bruker Minispec) standard plate geometries (C) of permanent magnets, they, as explained above, offer a huge bore diameter, while still having a reasonably homogeneous field.
This cylindrical design is only one class of designs that produce a uniform field inside a cavity within an array of permanent magnets. Other classes of design include wedge designs, proposed by Abele and Jensen, in which wedges of magnetized material are arranged to provide uniform field within cavities inside the design as shown.
The direction of magnetization of the wedges in (A) can be calculated using a set of rules given by Abele and allows for great freedom in the shape of the cavity. Another class of design is the magnetic mangle (B), proposed by Coey and Cugat, in which uniformly magnetized rods are arranged such that their magnetization matches that of a Halbach cylinder, as shown for a 6-rod design. This design greatly increases access to the region of uniform field, at the expense of the volume of uniform field being smaller than in the cylindrical designs (although this area can be made larger by increasing the number of component rods). Rotating the rods relative to each other results in many possibilities, including a dynamically variable field and various dipolar configurations. It can be seen that the designs shown in (A) and (B) are closely related to the ''k'' = 2 Halbach cylinder. Other very simple designs for a uniform field include separated magnets with soft iron return paths, as shown in figure (C).
In recent years, these Halbach dipoles have been used to conduct low-field NMR experiments. Compared to commercially available ( Bruker Minispec) standard plate geometries (C) of permanent magnets, they, as explained above, offer a huge bore diameter, while still having a reasonably homogeneous field.

 A Halbach array is a special arrangement of permanent
A Halbach array is a special arrangement of permanent magnet
A magnet is a material or object that produces a magnetic field. This magnetic field is invisible but is responsible for the most notable property of a magnet: a force that pulls on other ferromagnetic materials, such as iron, steel, nicke ...
s that augments the magnetic field on one side of the array while cancelling the field to near zero on the other side. This is achieved by having a spatially rotating pattern of magnetisation.
The rotating pattern of permanent magnets (on the front face; on the left, up, right, down) can be continued indefinitely and have the same effect. The effect of this arrangement is roughly similar to many horseshoe magnets placed adjacent to each other, with similar poles touching.
The principle was first invented by James (Jim) M. Winey of Magnepan
Magnepan is a private high-end audio loudspeaker manufacturer in White Bear Lake, Minnesota, United States. Their loudspeaker technology was conceived and implemented by engineer Jim Winey in 1969.
Overview
Magnepan's speaker design, sold under ...
in 1970, for the ideal case of continuously rotating magnetization, induced by a one-sided stripe-shaped coil.
The effect was also discovered by John C. Mallinson in 1973, and these "one-sided flux" structures were initially described by him as a "curiosity", although at the time he recognized from this discovery the potential for significant improvements in magnetic tape
Magnetic tape is a medium for magnetic storage made of a thin, magnetizable coating on a long, narrow strip of plastic film. It was developed in Germany in 1928, based on the earlier magnetic wire recording from Denmark. Devices that use magnet ...
technology.
Physicist Klaus Halbach, while at the Lawrence Berkeley National Laboratory
Lawrence Berkeley National Laboratory (LBNL), commonly referred to as the Berkeley Lab, is a United States national laboratory that is owned by, and conducts scientific research on behalf of, the United States Department of Energy. Located in ...
during the 1980s, independently invented the Halbach array to focus particle accelerator beams.
Linear arrays
Magnetization
 Although this magnetic flux distribution seems somewhat counter-intuitive to those familiar with simple bar magnets or solenoids, the reason for this flux distribution can be intuitively visualised using Mallinson's original diagram (note that it uses the negative ''y'' component, unlike the diagram in Mallinson's article). The diagram shows the field from a strip of ferromagnetic material with alternating magnetization in the ''y'' direction (top left) and in the ''x'' direction (top right). Note that the field above the plane is in the ''same'' direction for both structures, but the field below the plane is in ''opposite'' directions. The effect of superimposing both of these structures is shown in the figure.
The crucial point is that the flux will ''cancel below the plane and reinforce itself above the plane''. In fact, any magnetization pattern where the components of magnetization are out of phase with each other will result in a one-sided flux. The mathematical transform that shifts the phase of all components of some function by is called a Hilbert transform; the components of the magnetization vector can therefore be any Hilbert-transform pair (the simplest of which is simply , as shown in the diagram above).
Although this magnetic flux distribution seems somewhat counter-intuitive to those familiar with simple bar magnets or solenoids, the reason for this flux distribution can be intuitively visualised using Mallinson's original diagram (note that it uses the negative ''y'' component, unlike the diagram in Mallinson's article). The diagram shows the field from a strip of ferromagnetic material with alternating magnetization in the ''y'' direction (top left) and in the ''x'' direction (top right). Note that the field above the plane is in the ''same'' direction for both structures, but the field below the plane is in ''opposite'' directions. The effect of superimposing both of these structures is shown in the figure.
The crucial point is that the flux will ''cancel below the plane and reinforce itself above the plane''. In fact, any magnetization pattern where the components of magnetization are out of phase with each other will result in a one-sided flux. The mathematical transform that shifts the phase of all components of some function by is called a Hilbert transform; the components of the magnetization vector can therefore be any Hilbert-transform pair (the simplest of which is simply , as shown in the diagram above).
wavenumber
In the physical sciences, the wavenumber (also wave number or repetency) is the '' spatial frequency'' of a wave, measured in cycles per unit distance (ordinary wavenumber) or radians per unit distance (angular wavenumber). It is analogous to te ...
(i.e., the spatial frequency)
Applications
The advantages of one-sided flux distributions are twofold: * The field is twice as large on the side on which the flux is confined (in the idealized case). * There is no stray field produced (in the ideal case) on the opposite side. This helps with field confinement, usually a problem in the design of magnetic structures. Although one-sided flux distributions may seem somewhat abstract, they have a surprising number of applications ranging from therefrigerator magnet
A refrigerator magnet or fridge magnet is a small magnet, often attached to an artistic or whimsical ornament, which may be used to post items such as shopping lists, Christmas cards, child art or reminders on a refrigerator door, or which sim ...
through industrial applications such as the brushless DC motor
A DC motor is any of a class of rotary electrical motors that converts direct current (DC) electrical energy into mechanical energy. The most common types rely on the forces produced by induced magnetic fields due to flowing current in the coil ...
, voice coil
A voice coil (consisting of a former, collar, and winding) is the coil of wire attached to the apex of a loudspeaker cone. It provides the motive force to the cone by the reaction of a magnetic field to the current passing through it. The te ...
s, magnetic drug targeting to high-tech applications such as wiggler magnets used in particle accelerator
A particle accelerator is a machine that uses electromagnetic fields to propel charged particles to very high speeds and energies, and to contain them in well-defined beams.
Large accelerators are used for fundamental research in particle ...
s and free-electron lasers.
This device is also a key component of the Inductrack Maglev train
Maglev (derived from '' magnetic levitation''), is a system of train transportation that uses two sets of electromagnets: one set to repel and push the train up off the track, and another set to move the elevated train ahead, taking advantage ...
and Inductrack rocket-launch system, wherein the Halbach array repels loops of wire that form the track after the train has been accelerated to a speed able to lift.
extruded
Extrusion is a process used to create objects of a fixed cross-sectional profile by pushing material through a die of the desired cross-section. Its two main advantages over other manufacturing processes are its ability to create very complex c ...
magnet is exposed to a rotating field giving the ferrite particles in the magnetic compound a magnetization resulting in a one-sided flux distribution. This distribution increases the holding force of the magnet when placed on a permeable surface, compared to the holding force from, say, a uniform magnetization of the magnetic compound.
 Scaling up this design and adding a top sheet gives a wiggler magnet, used in
Scaling up this design and adding a top sheet gives a wiggler magnet, used in synchrotron
A synchrotron is a particular type of cyclic particle accelerator, descended from the cyclotron, in which the accelerating particle beam travels around a fixed closed-loop path. The magnetic field which bends the particle beam into its closed ...
s and free-electron lasers. Wiggler magnets wiggle, or oscillate, an electron beam perpendicular to the magnetic field. As the electrons are undergoing acceleration, they radiate electromagnetic energy in their flight direction, and as they interact with the light already emitted, photons along its line are emitted in phase, resulting in a "laser-like" monochromatic and coherent beam.
The design shown above is usually known as a Halbach wiggler. The magnetization vectors in the magnetized sheets rotate in the opposite senses to each other; above, the top sheet's magnetization vector rotates clockwise, and the bottom sheet's magnetization vector rotates counter-clockwise. This design is chosen so that the ''x'' components of the magnetic fields from the sheets cancel, and the ''y'' components reinforce, so that the field is given by
:
where ''k'' is the wavenumber
In the physical sciences, the wavenumber (also wave number or repetency) is the '' spatial frequency'' of a wave, measured in cycles per unit distance (ordinary wavenumber) or radians per unit distance (angular wavenumber). It is analogous to te ...
of the magnetic sheet given by the spacing between magnetic blocks with the same magnetization vector.
Variable linear arrays

 A series of magnetic rods, magnetized perpendicular to their axes, can be arranged into a Halbach array. If each rod is then rotated alternately through 90°, the resultant field moves from one side of plane of the rods to the other, as shown schematically in the figure.
This arrangement allows the field to effectively be turned on and off above or below the plane of the rods, depending on the rotation of the rods. Such a device makes an efficient mechanical magnetic latch requiring no power. A detailed study of this arrangement has shown that each rod is subject to a strong torque from its neighboring rods, and therefore requires mechanical stabilization. However, a simple and efficient solution, providing both stabilization and the ability to rotate each rod alternately, is simply to provide an equal-gearing arrangement on each rod, as shown in the figure.
A series of magnetic rods, magnetized perpendicular to their axes, can be arranged into a Halbach array. If each rod is then rotated alternately through 90°, the resultant field moves from one side of plane of the rods to the other, as shown schematically in the figure.
This arrangement allows the field to effectively be turned on and off above or below the plane of the rods, depending on the rotation of the rods. Such a device makes an efficient mechanical magnetic latch requiring no power. A detailed study of this arrangement has shown that each rod is subject to a strong torque from its neighboring rods, and therefore requires mechanical stabilization. However, a simple and efficient solution, providing both stabilization and the ability to rotate each rod alternately, is simply to provide an equal-gearing arrangement on each rod, as shown in the figure.
Cylinder

 A Halbach cylinder is a magnetized cylinder composed of
A Halbach cylinder is a magnetized cylinder composed of ferromagnetic
Ferromagnetism is a property of certain materials (such as iron) which results in a large observed magnetic permeability, and in many cases a large magnetic coercivity allowing the material to form a permanent magnet. Ferromagnetic materials ...
material producing (in the idealized case) an intense magnetic field confined entirely within the cylinder, with zero field outside. The cylinders can also be magnetized such that the magnetic field is entirely outside the cylinder, with zero field inside. Several magnetization distributions are shown in the figures.
The direction of magnetization within the ferromagnetic material, in plane perpendicular to the axis of the cylinder, is given by
:
where ''Mr'' is the ferromagnetic remanence
Remanence or remanent magnetization or residual magnetism is the magnetization left behind in a ferromagnetic material (such as iron) after an external magnetic field is removed. Colloquially, when a magnet is "magnetized", it has remanence. The ...
(A/m). A positive value of ''k'' − 1 gives an internal magnetic field, and a negative one gives an external magnetic field.
Ideally, these structures would be created from an infinite-length cylinder of magnetic material with the direction of magnetization continuously varying. The magnetic flux produced by this ideal design would be perfectly uniform and be entirely confined to either the bore of the cylinder or the outside of the cylinder. Of course, the ideal case of infinite length is not realizable, and in practice the finite length of the cylinders produces ''end effects'', which introduce non-uniformities in the field. The difficulty of manufacturing a cylinder with a continuously varying magnetization also usually leads to the design being broken into segments.
Applications
These cylindrical structures are used in devices such as brushless AC motors, magnetic couplings and high-field cylinders. Both brushless motors and coupling devices use multipole field arrangements: * Brushless motors or alternators typically use cylindrical designs in which all the flux is confined to the centre of the bore (such as ''k'' = 4 above, a 6-pole rotor) with the AC coils also contained within the bore. Such self-shielding motor or alternator designs are more efficient and produce higher torque or output than conventional motor or alternator designs. * Magnetic-coupling devices transmit torque through magnetically transparent barriers (that is, the barrier is non-magnetic or is magnetic but not affected by an applied magnetic field), for instance, between sealed containers or pressurised vessels. The optimal torque couplings consists of a pair of coaxially nested cylinders with opposite +''k'' and −''k'' flux magnetization patterns, as this configuration is the only system for infinitely long cylinders that produces a torque. In the lowest-energy state, the outer flux of the inner cylinder exactly matches the internal flux of the outer cylinder. Rotating one cylinder relative to the other from this state results in a restoring torque.Uniform fields
 For the special case of ''k'' = 2, the field inside the bore is uniform and is given by
:
where the inner and outer cylinder radii are ''R''i and ''R''o respectively. ''H'' is in the ''y'' direction. This is the simplest form of the Halbach cylinder, and it can be seen that if the ratio of outer to inner radii is greater than ''e'', the flux inside the bore actually exceeds the
For the special case of ''k'' = 2, the field inside the bore is uniform and is given by
:
where the inner and outer cylinder radii are ''R''i and ''R''o respectively. ''H'' is in the ''y'' direction. This is the simplest form of the Halbach cylinder, and it can be seen that if the ratio of outer to inner radii is greater than ''e'', the flux inside the bore actually exceeds the remanence
Remanence or remanent magnetization or residual magnetism is the magnetization left behind in a ferromagnetic material (such as iron) after an external magnetic field is removed. Colloquially, when a magnet is "magnetized", it has remanence. The ...
of the magnetic material used to create the cylinder. However, care has to be taken not to produce a field that exceeds the coercivity of the permanent magnets used, as this can result in demagnetization of the cylinder and the production of a much lower field than intended.
 This cylindrical design is only one class of designs that produce a uniform field inside a cavity within an array of permanent magnets. Other classes of design include wedge designs, proposed by Abele and Jensen, in which wedges of magnetized material are arranged to provide uniform field within cavities inside the design as shown.
The direction of magnetization of the wedges in (A) can be calculated using a set of rules given by Abele and allows for great freedom in the shape of the cavity. Another class of design is the magnetic mangle (B), proposed by Coey and Cugat, in which uniformly magnetized rods are arranged such that their magnetization matches that of a Halbach cylinder, as shown for a 6-rod design. This design greatly increases access to the region of uniform field, at the expense of the volume of uniform field being smaller than in the cylindrical designs (although this area can be made larger by increasing the number of component rods). Rotating the rods relative to each other results in many possibilities, including a dynamically variable field and various dipolar configurations. It can be seen that the designs shown in (A) and (B) are closely related to the ''k'' = 2 Halbach cylinder. Other very simple designs for a uniform field include separated magnets with soft iron return paths, as shown in figure (C).
In recent years, these Halbach dipoles have been used to conduct low-field NMR experiments. Compared to commercially available ( Bruker Minispec) standard plate geometries (C) of permanent magnets, they, as explained above, offer a huge bore diameter, while still having a reasonably homogeneous field.
This cylindrical design is only one class of designs that produce a uniform field inside a cavity within an array of permanent magnets. Other classes of design include wedge designs, proposed by Abele and Jensen, in which wedges of magnetized material are arranged to provide uniform field within cavities inside the design as shown.
The direction of magnetization of the wedges in (A) can be calculated using a set of rules given by Abele and allows for great freedom in the shape of the cavity. Another class of design is the magnetic mangle (B), proposed by Coey and Cugat, in which uniformly magnetized rods are arranged such that their magnetization matches that of a Halbach cylinder, as shown for a 6-rod design. This design greatly increases access to the region of uniform field, at the expense of the volume of uniform field being smaller than in the cylindrical designs (although this area can be made larger by increasing the number of component rods). Rotating the rods relative to each other results in many possibilities, including a dynamically variable field and various dipolar configurations. It can be seen that the designs shown in (A) and (B) are closely related to the ''k'' = 2 Halbach cylinder. Other very simple designs for a uniform field include separated magnets with soft iron return paths, as shown in figure (C).
In recent years, these Halbach dipoles have been used to conduct low-field NMR experiments. Compared to commercially available ( Bruker Minispec) standard plate geometries (C) of permanent magnets, they, as explained above, offer a huge bore diameter, while still having a reasonably homogeneous field.
Derivation in the ideal case
The method used to find the field created by the cylinder is mathematically very similar to that used to investigate a uniformly magnetised sphere. Because of the symmetry of the arrangement along the cylinder's axis, the problem can be treated as two-dimensional. Work in plane-polar coordinates with associated unit vectors and , and let the cylinder have radial extent . Then the magnetisation in the cylinder walls, which has magnitude , rotates smoothly as : while the magnetisation vanishes outside the walls, that is for the bore and surroundings . By definition, the auxiliary magnetic field strength is related to the magnetisation and magnetic flux density by . UsingGauss' law
In physics and electromagnetism, Gauss's law, also known as Gauss's flux theorem, (or sometimes simply called Gauss's theorem) is a law relating the distribution of electric charge to the resulting electric field. In its integral form, it s ...
, this is equivalently
Since the problem is static there are no free currents and all time derivatives vanish, so Ampère's law additionally requires , where is the magnetic scalar potential (up to a sign under some definitions). Substituting this back into the previous Equation governing and , we find that we need to solve
which has the form of Poisson's equation
Poisson's equation is an elliptic partial differential equation of broad utility in theoretical physics. For example, the solution to Poisson's equation is the potential field caused by a given electric charge or mass density distribution; with ...
.
Consider now the boundary conditions at the cylinder-air interfaces and . Integrating over a small loop straddling the boundary and applying Stokes' theorem
Stokes's theorem, also known as the Kelvin–Stokes theorem Nagayoshi Iwahori, et al.:"Bi-Bun-Seki-Bun-Gaku" Sho-Ka-Bou(jp) 1983/12Written in Japanese)Atsuo Fujimoto;"Vector-Kai-Seki Gendai su-gaku rekucha zu. C(1)" :ja:培風館, Bai-Fu-Kan( ...
requires that the parallel component of is continuous. This in turn requires that is continuous across the boundary. (More properly this implies that must differ by a ''constant'' across the boundary, but since the physical quantities we are interested in depend on gradients of this potential, we can arbitrarily set the constant to zero for convenience.) To obtain a second set of conditions, integrate Equation across a small volume straddling the boundary and apply the divergence theorem
In vector calculus, the divergence theorem, also known as Gauss's theorem or Ostrogradsky's theorem, reprinted in is a theorem which relates the '' flux'' of a vector field through a closed surface to the ''divergence'' of the field in the ...
to find
:
where the notation