George Boole

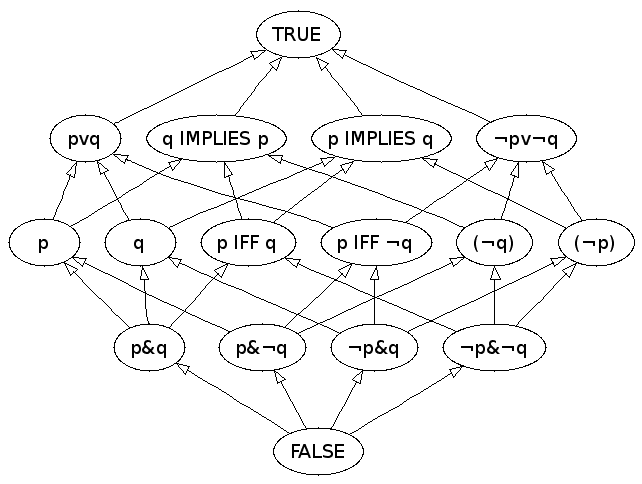
George Boole (; 2 November 1815 – 8 December 1864) was a largely self-taught English mathematician, philosopher, and logician, most of whose short career was spent as the first professor of mathematics at Queen's College, Cork in Ireland. He worked in the fields of differential equations and algebraic logic, and is best known as the author of ''The Laws of Thought'' (1854) which contains Boolean algebra. Boolean logic is credited with laying the foundations for the Information Age.

Early life

Boole was born in 1815 in Lincoln, Lincolnshire, England, the son of John Boole senior (1779–1848), a shoemaker and Mary Ann Joyce. He had a primary school education, and received lessons from his father, but due to a serious decline in business, he had little further formal and academic teaching. William Brooke, a bookseller in Lincoln, may have helped him with Latin, which he may also have learned at the school of Thomas Bainbridge. He was self-taught in modern languages.Hill, p. 149
Google Books
. In fact, when a local newspaper printed his translation of a Latin poem, a scholar accused him of plagiarism under the pretence that he was not capable of such achievements. At age 16, Boole became the breadwinner for his parents and three younger siblings, taking up a junior teaching position in Doncaster at Heigham's School. Rhees, Rush. (1954) "George Boole as Student and Teacher. By Some of His Friends and Pupils", ''Proceedings of the Royal Irish Academy. Section A: Mathematical and Physical Sciences''. Vol. 57. Royal Irish Academy He taught briefly in Liverpool.

Boole participated in the Lincoln Mechanics' Institute, in the Greyfriars, Lincoln, which was founded in 1833. Edward Bromhead, who knew John Boole through the institution, helped George Boole with mathematics books and he was given the calculus text of Sylvestre François Lacroix by the Rev. George Stevens Dickson of St Swithin's, Lincoln. Without a teacher, it took him many years to master calculus.

At age 19, Boole successfully established his own school in Lincoln: Free School Lane. Four years later he took over Hall's Academy in Waddington, outside Lincoln, following the death of Robert Hall. In 1840, he moved back to Lincoln, where he ran a boarding school. Boole immediately became involved in the Lincoln Topographical Society, serving as a member of the committee, and presenting a paper entitled "On the origin, progress, and tendencies of polytheism", especially amongst the ancient Egyptians and Persians, and in modern India.'

Boole became a prominent local figure, an admirer of John Kaye, the bishop. He took part in the local campaign for early closing. With Edmund Larken and others he set up a building society in 1847. He associated also with the Chartist Thomas Cooper, whose wife was a relation.

From 1838 onwards, Boole was making contacts with sympathetic British academic mathematicians and reading more widely. He studied algebra in the form of symbolic methods, as far as these were understood at the time, and began to publish research papers.

Professorship and Life in Cork

Boole's status as a mathematician was recognised by his appointment in 1849 as the first professor of mathematics at Queen's College, Cork (now University College Cork (UCC)) in Ireland. He met his future wife, Mary Everest, there in 1850 while she was visiting her uncle John Ryall who was professor of Greek. They married some years later in 1855. He maintained his ties with Lincoln, working there with E. R. Larken in a campaign to reduce prostitution.Hill, p. 138 note 4
Google Books
.

Honours and awards

In 1844, Boole's paper "On a General Method in Analysis" won the first gold prize for mathematics awarded by the Royal Society. He was awarded the Keith Medal by the Royal Society of Edinburgh in 1855 and was elected a Fellow of the Royal Society (FRS) in 1857. He received honorary degrees of LL.D. from the University of Dublin and the University of Oxford.

Works

Boole's first published paper was "Researches in the theory of analytical transformations, with a special application to the reduction of the general equation of the second order", printed in the '' Cambridge Mathematical Journal'' in February 1840 (Volume 2, No. 8, pp. 64–73), and it led to a friendship between Boole and Duncan Farquharson Gregory, the editor of the journal. His works are in about 50 articles and a few separate publications.

In 1841, Boole published an influential paper in early invariant theory. He received a medal from the Royal Society for his memoir of 1844, "On a General Method in Analysis". It was a contribution to the theory of linear differential equations, moving from the case of constant coefficients on which he had already published, to variable coefficients. The innovation in operational methods is to admit that operations may not commute. In 1847, Boole published ''The Mathematical Analysis of Logic'', the first of his works on symbolic logic.

Differential equations

Boole completed two systematic treatises on mathematical subjects during his lifetime. The ''Treatise on Differential Equations'' appeared in 1859, and was followed, the next year, by a ''Treatise on the Calculus of Finite Differences'', a sequel to the former work.

Analysis

In 1857, Boole published the treatise "On the Comparison of Transcendent, with Certain Applications to the Theory of Definite Integrals", in which he studied the sum of residues of a rational function. Among other results, he proved what is now called Boole's identity:
:$\mathrm \left\ = \frac$
for any real numbers ''a''_''k'' > 0, ''b''_''k'', and ''t'' > 0. Generalisations of this identity play an important role in the theory of the Hilbert transform.

Symbolic logic

In 1847, Boole published the pamphlet ''Mathematical Analysis of Logic''. He later regarded it as a flawed exposition of his logical system and wanted '' An Investigation of the Laws of Thought on Which are Founded the Mathematical Theories of Logic and Probabilities'' to be seen as the mature statement of his views. Contrary to widespread belief, Boole never intended to criticise or disagree with the main principles of Aristotle's logic. Rather he intended to systematise it, to provide it with a foundation, and to extend its range of applicability. Boole's initial involvement in logic was prompted by a current debate on quantification, between Sir William Hamilton who supported the theory of "quantification of the predicate", and Boole's supporter Augustus De Morgan who advanced a version of De Morgan duality, as it is now called. Boole's approach was ultimately much further reaching than either sides' in the controversy. It founded what was first known as the "algebra of logic" tradition.Witold Marciszewski (editor), ''Dictionary of Logic as Applied in the Study of Language'' (1981), pp. 194–5.

Among his many innovations is his principle of wholistic reference, which was later, and probably independently, adopted by Gottlob Frege and by logicians who subscribe to standard first-order logic. A 2003 article provides a systematic comparison and critical evaluation of Aristotelian logic and Boolean logic; it also reveals the centrality of holistic reference in Boole's philosophy of logic.

1854 definition of the universe of discourse

In every discourse, whether of the mind conversing with its own thoughts, or of the individual in his intercourse with others, there is an assumed or expressed limit within which the subjects of its operation are confined. The most unfettered discourse is that in which the words we use are understood in the widest possible application, and for them, the limits of discourse are co-extensive with those of the universe itself. But more usually we confine ourselves to a less spacious field. Sometimes, in discoursing of men we imply (without expressing the limitation) that it is of men only under certain circumstances and conditions that we speak, as of civilised men, or of men in the vigour of life, or of men under some other condition or relation. Now, whatever may be the extent of the field within which all the objects of our discourse are found, that field may properly be termed the universe of discourse. Furthermore, this universe of discourse is in the strictest sense the ultimate subject of the discourse.

Treatment of addition in logic

Boole conceived of "elective symbols" of his kind as an algebraic structure. But this general concept was not available to him: he did not have the segregation standard in abstract algebra of postulated (axiomatic) properties of operations, and deduced properties. Andrei Nikolaevich Kolmogorov, Adolf Pavlovich Yushkevich, ''Mathematics of the 19th century: mathematical logic, algebra, number theory, probability theory'' (2001), pp. 15 (note 15)–16
Google Books
. His work was a beginning to the algebra of sets, again not a concept available to Boole as a familiar model. His pioneering efforts encountered specific difficulties, and the treatment of addition was an obvious difficulty in the early days.

Boole replaced the operation of multiplication by the word "and" and addition by the word "or". But in Boole's original system, + was a partial operation: in the language of set theory it would correspond only to disjoint union of subsets. Later authors changed the interpretation, commonly reading it as exclusive or, or in set theory terms symmetric difference; this step means that addition is always defined.

In fact, there is the other possibility, that + should be read as disjunction. This other possibility extends from the disjoint union case, where exclusive or and non-exclusive or both give the same answer. Handling this ambiguity was an early problem of the theory, reflecting the modern use of both Boolean rings and Boolean algebras (which are simply different aspects of one type of structure). Boole and Jevons struggled over just this issue in 1863, in the form of the correct evaluation of ''x'' + ''x''. Jevons argued for the result ''x'', which is correct for + as disjunction. Boole kept the result as something undefined. He argued against the result 0, which is correct for exclusive or, because he saw the equation ''x'' + ''x'' = 0 as implying ''x'' = 0, a false analogy with ordinary algebra.

Probability theory

The second part of the ''Laws of Thought'' contained a corresponding attempt to discover a general method in probabilities. Here the goal was algorithmic: from the given probabilities of any system of events, to determine the consequent probability of any other event logically connected with those events.

Death

In late November 1864, Boole walked, in heavy rain, from his home at Lichfield Cottage in Ballintemple to the university, a distance of three miles, and lectured wearing his wet clothes. He soon became ill, developing pneumonia. As his wife believed that remedies should resemble their cause, she wrapped him in wet blankets – the wet having brought on his illness. Boole's condition worsened and on 8 December 1864, he died of fever-induced pleural effusion.

He was buried in the Church of Ireland cemetery of St Michael's, Church Road, Blackrock (a suburb of Cork). There is a commemorative plaque inside the adjoining church.

Legacy

Boole is the namesake of the branch of algebra known as Boolean algebra, as well as the namesake of the lunar crater Boole. The keyword ''Bool'' represents a Boolean datatype in many programming languages, though Pascal and Java, among others, both use the full name ''Boolean''. The library, underground lecture theatre complex and the Boole Centre for Research in Informatics at University College Cork are named in his honour. A road called ''Boole Heights'' in Bracknell, Berkshire is named after him.

19th-century development

Boole's work was extended and refined by a number of writers, beginning with William Stanley Jevons, who also authored the article about Boole in the ''Encyclopaedia Britannica''. Augustus De Morgan had worked on the logic of relations, and Charles Sanders Peirce integrated his work with Boole's during the 1870s. Ivor Grattan-Guinness, Gérard Bornet, ''George Boole: Selected manuscripts on logic and its philosophy'' (1997), p. xlvi
Google Books
. Other significant figures were Platon Sergeevich Poretskii, and William Ernest Johnson. The conception of a Boolean algebra structure on equivalent statements of a propositional calculus is credited to Hugh MacColl (1877), in work surveyed 15 years later by Johnson. Surveys of these developments were published by Ernst Schröder, Louis Couturat, and Clarence Irving Lewis.

20th-century development

In 1921, the economist John Maynard Keynes published a book on probability theory, ''A Treatise of Probability''. Keynes believed that Boole had made a fundamental error in his definition of independence which vitiated much of his analysis. In his book ''The Last Challenge Problem'', David Miller provides a general method in accord with Boole's system and attempts to solve the problems recognised earlier by Keynes and others. Theodore Hailperin showed much earlier that Boole had used the correct mathematical definition of independence in his worked out problems.

Boole's work and that of later logicians initially appeared to have no engineering uses. Claude Shannon attended a philosophy class at the University of Michigan which introduced him to Boole's studies. Shannon recognised that Boole's work could form the basis of mechanisms and processes in the real world and that it was therefore highly relevant. In 1937 Shannon went on to write a master's thesis, at the Massachusetts Institute of Technology, in which he showed how Boolean algebra could optimise the design of systems of electromechanical relays then used in telephone routing switches. He also proved that circuits with relays could solve Boolean algebra problems. Employing the properties of electrical switches to process logic is the basic concept that underlies all modern electronic digital computers. Victor Shestakov at Moscow State University (1907–1987) proposed a theory of electric switches based on Boolean logic even earlier than Claude Shannon in 1935 on the testimony of Soviet logicians and mathematicians Sofya Yanovskaya, Gaaze-Rapoport, Roland Dobrushin, Lupanov, Medvedev and Uspensky, though they presented their academic theses in the same year, 1938. But the first publication of Shestakov's result took place only in 1941 (in Russian). Hence, Boolean algebra became the foundation of practical digital circuit design; and Boole, via Shannon and Shestakov, provided the theoretical grounding for the Information Age.

21st-century celebration

The year 2015 saw the 200th anniversary of Boole's birth. To mark the bicentenary year, University College Cork joined admirers of Boole around the world to celebrate his life and legacy.

UCC's George Boole 200 project, featured events, student outreach activities and academic conferences on Boole's legacy in the digital age, including a new edition of Desmond MacHale's 1985 biography '' The Life and Work of George Boole: A Prelude to the Digital Age'', 2014.

The search engine Google marked the 200th anniversary of his birth on 2 November 2015 with an algebraic reimaging of its Google Doodle.

Views

Boole's views were given in four published addresses: ''The Genius of Sir Isaac Newton''; ''The Right Use of Leisure''; ''The Claims of Science''; and ''The Social Aspect of Intellectual Culture''. The first of these was from 1835 when Charles Anderson-Pelham, 1st Earl of Yarborough gave a bust of Newton to the Mechanics' Institute in Lincoln. The second justified and celebrated in 1847 the outcome of the successful campaign for early closing in Lincoln, headed by Alexander Leslie-Melville, of Branston Hall. ''The Claims of Science'' was given in 1851 at Queen's College, Cork. ''The Social Aspect of Intellectual Culture'' was also given in Cork, in 1855 to the Cuvierian Society.

Though his biographer Des MacHale describes Boole as an "agnostic deist", Boole read a wide variety of Christian theology. Combining his interests in mathematics and theology, he compared the Christian trinity of Father, Son, and Holy Ghost with the three dimensions of space, and was attracted to the Hebrew conception of God as an absolute unity. Boole considered converting to Judaism but in the end was said to have chosen Unitarianism. ^{eference?/sup> Boole came to speak against what he saw as "prideful" scepticism, and instead favoured the belief in a "Supreme Intelligent Cause". He also declared "I firmly believe, for the accomplishment of a purpose of the Divine Mind." In addition, he stated that he perceived "teeming evidences of surrounding design" and concluded that "the course of this world is not abandoned to chance and inexorable fate."}

Two influences on Boole were later claimed by his wife, Mary Everest Boole: a universal mysticism tempered by Jewish thought, and Indian logic.Jonardon Ganeri (2001), ''Indian Logic: a reader'', Routledge, p. 7,
Google Books
. Mary Boole stated that an adolescent mystical experience provided for his life's work:

My husband told me that when he was a lad of seventeen a thought struck him suddenly, which became the foundation of all his future discoveries. It was a flash of psychological insight into the conditions under which a mind most readily accumulates knowledge ..For a few years he supposed himself to be convinced of the truth of "the Bible" as a whole, and even intended to take orders as a clergyman of the English Church. But by the help of a learned Jew in Lincoln he found out the true nature of the discovery which had dawned on him. This was that man's mind works by means of some mechanism which "functions normally towards Monism."Boole, Mary Everest ''Indian Thought and Western Science in the Nineteenth Century'', Boole, Mary Everest ''Collected Works'' eds. E. M. Cobham and E. S. Dummer, London, Daniel 1931 pp.947–967

In Ch. 13 of ''Laws of Thought'' Boole used examples of propositions from Baruch Spinoza and Samuel Clarke. The work contains some remarks on the relationship of logic to religion, but they are slight and cryptic. Boole was apparently disconcerted at the book's reception just as a mathematical toolset:

George afterwards learned, to his great joy, that the same conception of the basis of Logic was held by Leibniz, the contemporary of Newton. De Morgan, of course, understood the formula in its true sense; he was Boole's collaborator all along. Herbert Spencer, Jowett, and Robert Leslie Ellis understood, I feel sure; and a few others, but nearly all the logicians and mathematicians ignored 53the statement that the book was meant to throw light on the nature of the human mind; and treated the formula entirely as a wonderful new method of reducing to logical order masses of evidence about external fact.

Mary Boole claimed that there was profound influence – via her uncle George Everest – of Indian thought in general and Indian logic, in particular, on George Boole, as well as on Augustus De Morgan and Charles Babbage:

Think what must have been the effect of the intense Hinduizing of three such men as Babbage, De Morgan, and George Boole on the mathematical atmosphere of 1830–65. What share had it in generating the Vector Analysis and the mathematics by which investigations in physical science are now conducted?

Boole maintained that:

Family

In 1855, Boole married Mary Everest (niece of George Everest), who later wrote several educational works on her husband's principles.

The Booles had five daughters:
* Mary Ellen (1856–1908) who married the mathematician and author Charles Howard Hinton and had four children: George (1882–1943), Eric (*1884), William (1886–1909) and Sebastian (1887–1923), inventor of the Jungle gym. After the sudden death of her husband, Mary Ellen committed suicide in Washington, D.C. in May 1908. Sebastian had three children:
** Jean Hinton (married name Rosner) (1917–2002), a peace activist.
** William H. Hinton (1919–2004) visited China in the 1930s and 40s and wrote an influential account of the Communist land reform.
** Joan Hinton (1921–2010) worked for the Manhattan Project and lived in China from 1948 until her death on 8 June 2010; she was married to Sid Engst.
* Margaret (1858–1935), married Edward Ingram Taylor, an artist.
** Their elder son Geoffrey Ingram Taylor became a mathematician and a Fellow of the Royal Society.
** Their younger son Julian Taylor was a professor of surgery.
* Alicia (1860–1940), who made important contributions to four-dimensional geometry.
** Her son Leonard Stott, a medical doctor and tuberculosis pioneer, invented a portable X-ray machine, a pneumothorax apparatus, and system of navigation based on spherical coordinates.D. MacHale, ''The Life and Work of George Boole: A Prelude to the Digital Age'', Cork University Press, 2014. cited in
The Extraordinary Case of the Boole Family
'' by Moira Chas
* Lucy Everest (1862–1904), who was the first female professor of chemistry in England.
* Ethel Lilian (1864–1960), who married the Polish scientist and revolutionary Wilfrid Michael Voynich and was the author of the novel ''The Gadfly''.

See also

Concepts

* Boolean algebra, a logical calculus of truth values or set membership
* Boolean algebra (structure), a set with operations resembling logical ones
* Boolean circuit, a mathematical model for digital logical circuits.
* Boolean data type is a data type, having two values (usually denoted true and false)
* Boolean expression, an expression in a programming language that produces a Boolean value when evaluated
* Boolean function, a function that determines Boolean values or operators
* Boolean model (probability theory), a model in stochastic geometry
* Boolean network, a certain network consisting of a set of Boolean variables whose state is determined by other variables in the network
* Boolean processor, a 1-bit variables computing unit
* Boolean ring, a ring consisting of idempotent elements
* Boolean satisfiability problem
* Boole's syllogistic is a logic invented by 19th-century British mathematician George Boole, which attempts to incorporate the "empty set".
* Laws of thought
* Principle of wholistic reference

Other

* List of Boolean algebra topics
* List of pioneers in computer science

Notes

References

* Walker, A. (ed) (2019) ''George Boole's Lincoln, 1815–49.'' The Survey of Lincoln, Vol.16.
* University College Cork, ''George Boole 200 Bicentenary Celebration''
GeorgeBoole.com

* Ivor Grattan-Guinness, ''The Search for Mathematical Roots 1870–1940''. Princeton University Press. 2000.
* Francis Hill (1974), ''Victorian Lincoln''
Google Books
.
* Des MacHale, '' George Boole: His Life and Work''
Boole Press
1985.
* Des MacHale, '' The Life and Work of George Boole: A Prelude to the Digital Age'' (new edition)
Cork University Press
. 2014
* Stephen Hawking, '' God Created the Integers''. Running Press, Philadelphia. 2007.

External links

Roger Parsons' article on Boole
*
*


by George Boole; a transcription of an article which originally appeared in ''Cambridge and Dublin Mathematical Journal'', Vol. III (1848), pp. 183–98.

George Boole's work as first Professor of Mathematics in University College, Cork, Ireland


George Boole website

Author profile
in the database zbMATH
*

{{DEFAULTSORT:Boole, George
1815 births
1864 deaths
19th-century British mathematicians
19th-century British non-fiction writers
19th-century British philosophers
19th-century British writers
19th-century English mathematicians
19th-century English non-fiction writers
19th-century English philosophers
19th-century English writers
19th-century essayists
19th-century translators
Academics of Queens College Cork
Boolean algebra
British deists
British essayists
British innovators
British male non-fiction writers
British mathematicians
British translators
British Unitarians
Respiratory disease deaths in Ireland
English essayists
English innovators
English logicians
English mathematicians
English non-fiction writers
English translators
English Unitarians
Fellows of the Royal Society
History of algebra
History of logic
History of mathematics
History of philosophy
History of science
Mathematical logicians
People from Lincoln, England
Philosophers of logic
Philosophers of mathematics
Probability theorists
Royal Medal winners
Victorian writers