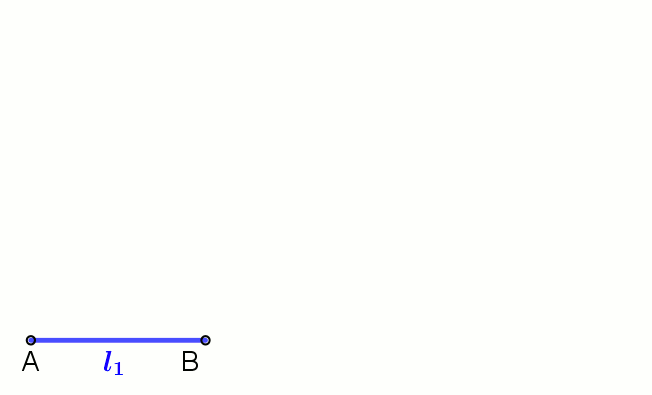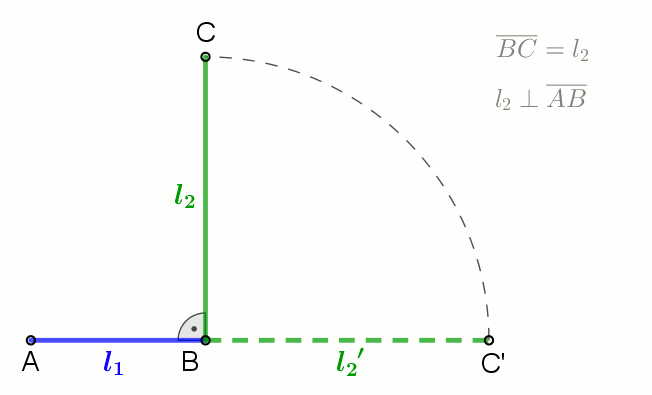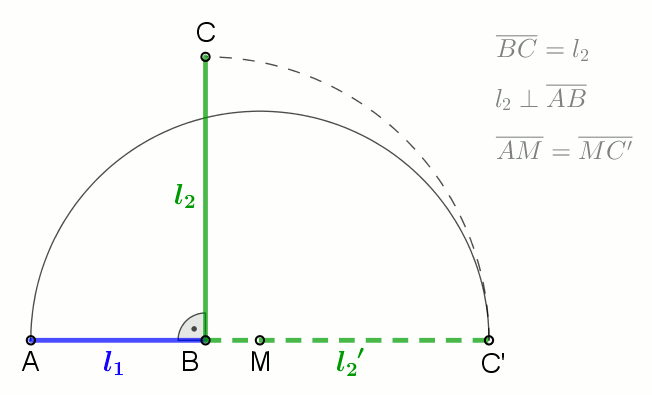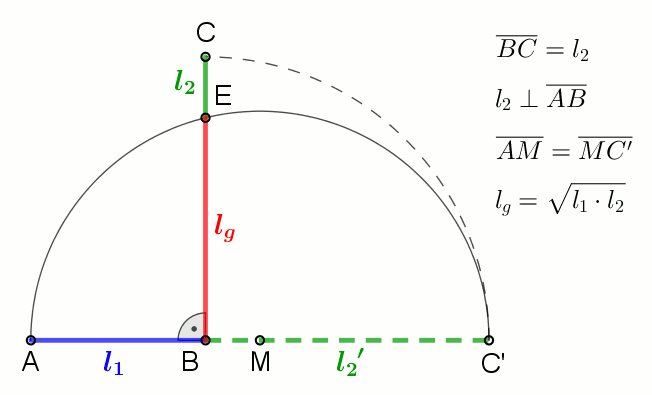
In mathematics, the geometric mean is a
mean
There are several kinds of mean in mathematics, especially in statistics. Each mean serves to summarize a given group of data, often to better understand the overall value ( magnitude and sign) of a given data set.
For a data set, the '' ar ...
or
average
In ordinary language, an average is a single number taken as representative of a list of numbers, usually the sum of the numbers divided by how many numbers are in the list (the arithmetic mean). For example, the average of the numbers 2, 3, 4, 7 ...
which indicates a
central tendency of a set of numbers by using the product of their values (as opposed to the
arithmetic mean
In mathematics and statistics, the arithmetic mean ( ) or arithmetic average, or just the '' mean'' or the ''average'' (when the context is clear), is the sum of a collection of numbers divided by the count of numbers in the collection. The co ...
which uses their sum). The geometric mean is defined as the
th root of the
product of numbers, i.e., for a set of numbers , the geometric mean is defined as
:
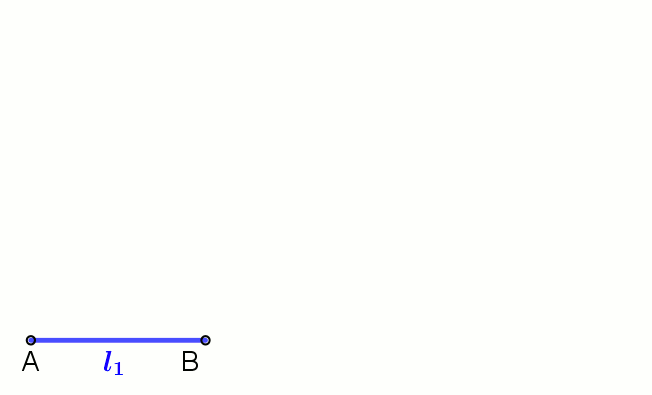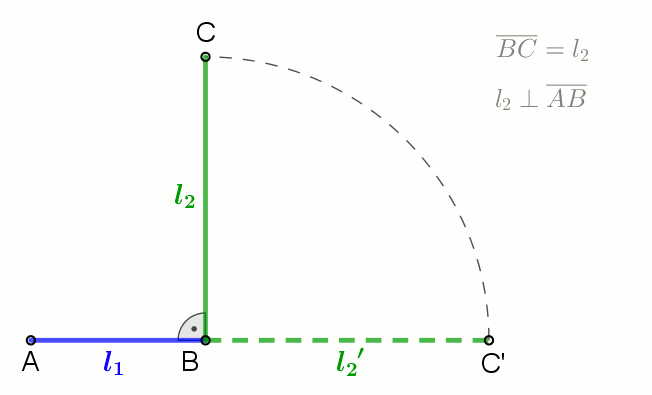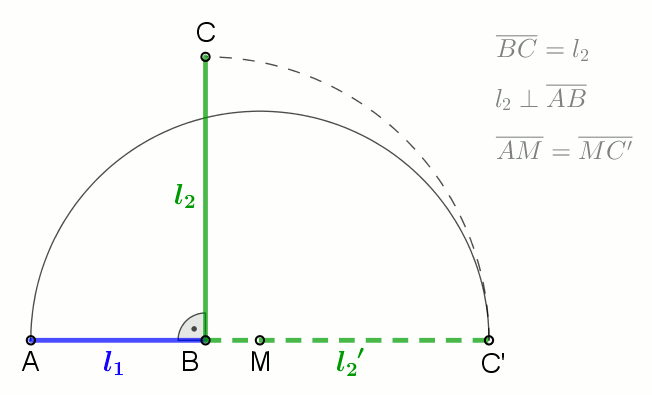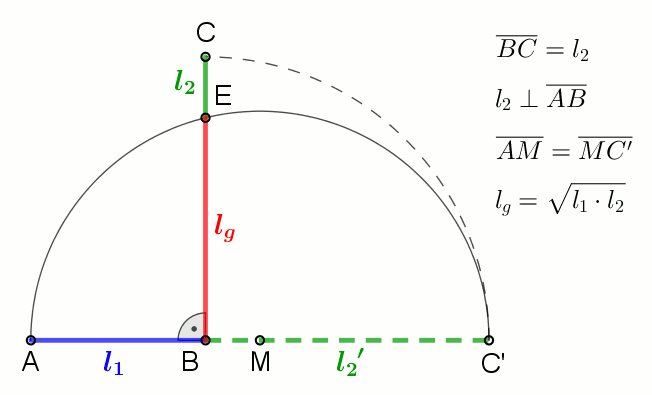 In mathematics, the geometric mean is a
In mathematics, the geometric mean is a
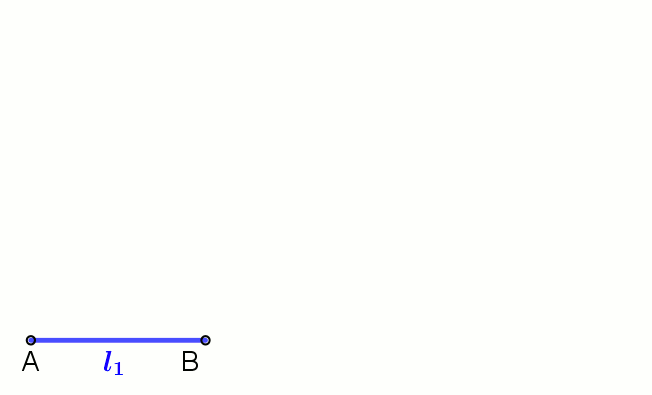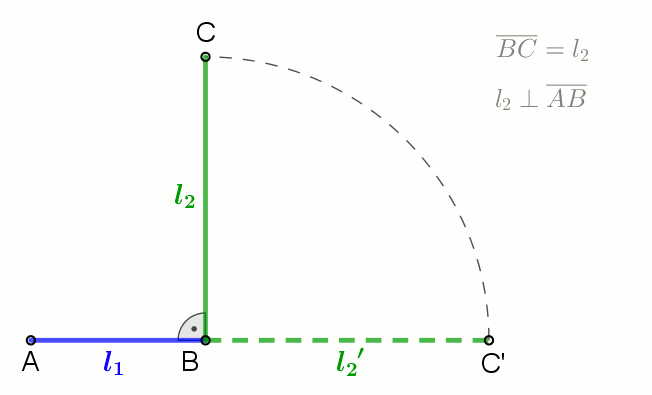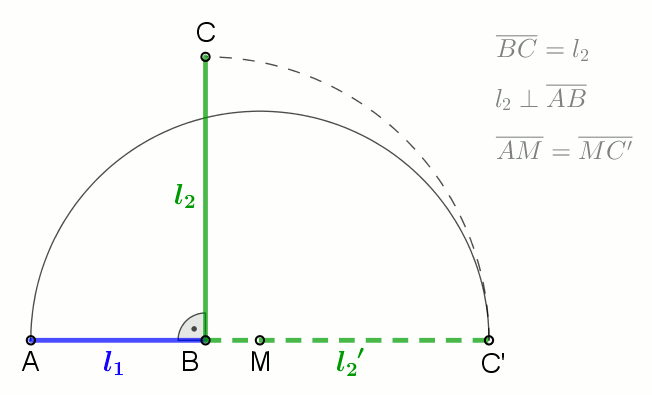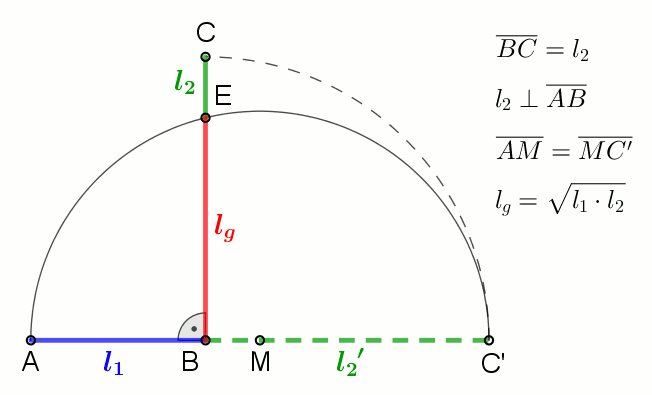 In mathematics, the geometric mean is a
In mathematics, the geometric mean is a