Gamma distribution

In probability theory and statistics, the gamma distribution is a two-parameter family of continuous probability distributions. The exponential distribution, Erlang distribution, and chi-square distribution are special cases of the gamma distribution. There are two equivalent parameterizations in common use:
#With a shape parameter $k$ and a scale parameter $\theta$.
#With a shape parameter $\alpha = k$ and an inverse scale parameter $\beta = 1/ \theta$ , called a rate parameter.
In each of these forms, both parameters are positive real numbers.

The gamma distribution is the maximum entropy probability distribution (both with respect to a uniform base measure and a $1/x$ base measure) for a random variable $X$ for which E 'X''= ''kθ'' = ''α''/''β'' is fixed and greater than zero, and E n(''X'')= ''ψ''(''k'') + ln(''θ'') = ''ψ''(''α'') − ln(''β'') is fixed (''ψ'' is the digamma function).

Definitions

The parameterization with ''k'' and ''θ'' appears to be more common in econometrics and other applied fields, where the gamma distribution is frequently used to model waiting times. For instance, in life testing, the waiting time until death is a random variable that is frequently modeled with a gamma distribution. See Hogg and Craig for an explicit motivation.

The parameterization with $\alpha$ and $\beta$ is more common in Bayesian statistics, where the gamma distribution is used as a conjugate prior distribution for various types of inverse scale (rate) parameters, such as the ''λ'' of an exponential distribution or a Poisson distribution – or for that matter, the ''β'' of the gamma distribution itself. The closely related inverse-gamma distribution is used as a conjugate prior for scale parameters, such as the variance of a normal distribution.

If ''k'' is a positive integer, then the distribution represents an Erlang distribution; i.e., the sum of ''k'' independent exponentially distributed random variables, each of which has a mean of ''θ''.

Characterization using shape ''α'' and rate ''β''

The gamma distribution can be parameterized in terms of a shape parameter ''α'' = ''k'' and an inverse scale parameter ''β'' = 1/''θ'', called a rate parameter. A random variable ''X'' that is gamma-distributed with shape ''α'' and rate ''β'' is denoted

:$X \sim \Gamma(\alpha, \beta) \equiv \operatorname(\alpha,\beta)$

The corresponding probability density function in the shape-rate parameterization is

:
\begin
f(x;\alpha,\beta) & = \frac \quad \text x > 0 \quad \alpha, \beta > 0, \\ pt\end

where $\Gamma(\alpha)$ is the gamma function.
For all positive integers, $\Gamma(\alpha)=(\alpha-1)!$.

The cumulative distribution function is the regularized gamma function:

:$F(x;\alpha,\beta) = \int_0^x f(u;\alpha,\beta)\,du= \frac,$

where $\gamma(\alpha, \beta x)$ is the lower incomplete gamma function.

If ''α'' is a positive integer (i.e., the distribution is an Erlang distribution), the cumulative distribution function has the following series expansion:

:$F(x;\alpha,\beta) = 1-\sum_^ \frac e^ = e^ \sum_^ \frac.$

Characterization using shape ''k'' and scale ''θ''

A random variable ''X'' that is gamma-distributed with shape ''k'' and scale ''θ'' is denoted by

:$X \sim \Gamma(k, \theta) \equiv \operatorname(k, \theta)$

The probability density function using the shape-scale parametrization is

:$f(x;k,\theta) = \frac \quad \text x > 0 \text k, \theta > 0.$

Here Γ(''k'') is the gamma function evaluated at ''k''.

The cumulative distribution function is the regularized gamma function:

:$F(x;k,\theta) = \int_0^x f(u;k,\theta)\,du = \frac,$

where $\gamma\left(k, \frac\right)$ is the lower incomplete gamma function.

It can also be expressed as follows, if ''k'' is a positive integer (i.e., the distribution is an Erlang distribution):Papoulis, Pillai, ''Probability, Random Variables, and Stochastic Processes'', Fourth Edition

:$F(x;k,\theta) = 1-\sum_^ \frac \left(\frac \right)^i e^ = e^ \sum_^\infty \frac \left( \frac \right)^i.$

Both parametrizations are common because either can be more convenient depending on the situation.

Properties

Mean and variance

The mean of gamma distribution is given by the product of its shape and scale parameters:
:$\mu = k\theta = \alpha/\beta$
The variance is:
:$\sigma^2 = k \theta^2 = \alpha/\beta^2$
The square root of the inverse shape parameter gives the coefficient of variation:
:$\sigma/\mu = k^ = 1/\sqrt$

Skewness

The skewness of the gamma distribution only depends on its shape parameter, ''k'', and it is equal to $2/\sqrt.$

Higher moments

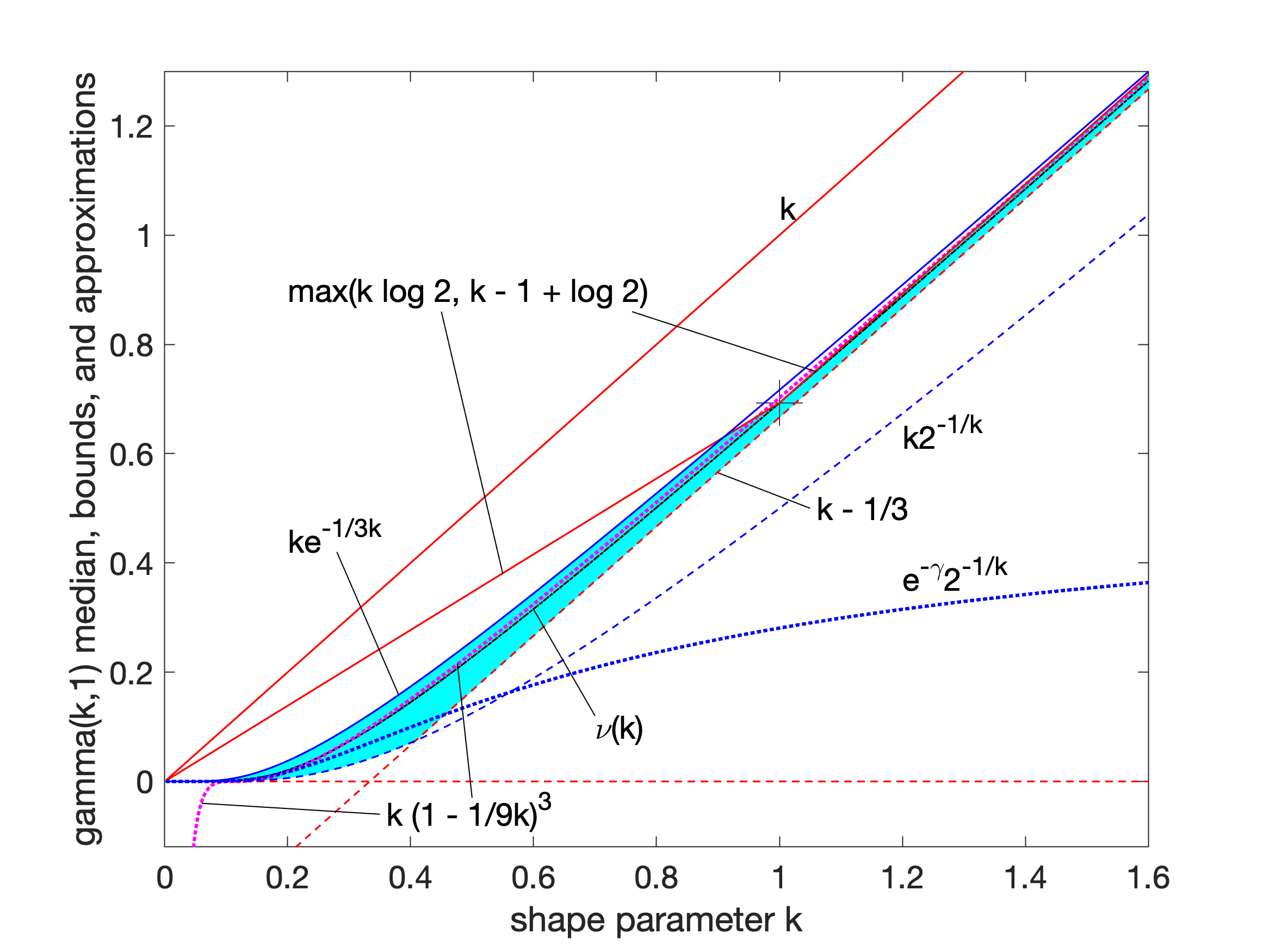
The ''n''th raw moment is given by:
:
\mathrm ^n= \theta^n \frac = \theta^n \prod_^n(k+i-1) \; \text n=1, 2, \ldots.

Median approximations and bounds

Unlike the mode and the mean, which have readily calculable formulas based on the parameters, the median does not have a closed-form equation. The median for this distribution is the value $\nu$ such that
: $\frac \int_0^ x^ e^ dx = \frac.$

A rigorous treatment of the problem of determining an asymptotic expansion and bounds for the median of the gamma distribution was handled first by Chen and Rubin, who proved that (for $\theta = 1$)
: $k - \frac < \nu(k) < k,$
where $\mu(k) = k$ is the mean and $\nu(k)$ is the median of the $\text(k,1)$ distribution. For other values of the scale parameter, the mean scales to $\mu = k\theta$, and the median bounds and approximations would be similarly scaled by $\theta$.

K. P. Choi found the first five terms in a Laurent series asymptotic approximation of the median by comparing the median to Ramanujan's $\theta$ function. Berg and Pedersen found more terms:
: $\nu(k) = k - \frac + \frac + \frac + \frac - \frac - O\left(\frac\right) + \cdots$

Partial sums of these series are good approximations for high enough $k$; they are not plotted in the figure, which is focused on the low-$k$ region that is less well approximated.

Berg and Pedersen also proved many properties of the median, showing that it is a convex function of $k$,Berg, Christian and Pedersen, Henrik L
"Convexity of the median in the gamma distribution"
and that the asymptotic behavior near $k = 0$ is $\nu(k) \approx e^2^$ (where $\gamma$ is the Euler–Mascheroni constant), and that for all $k > 0$ the median is bounded by $k 2^ < \nu(k) < k e^$.

A closer linear upper bound, for $k \ge 1$ only, was provided in 2021 by Gaunt and Merkle, relying on the Berg and Pedersen result that the slope of $\nu(k)$ is everywhere less than 1:
: $\nu(k) \le k - 1 + \log2 ~~$ for $k \ge 1$ (with equality at $k = 1$)
which can be extended to a bound for all $k > 0$ by taking the max with the chord shown in the figure, since the median was proved convex.

An approximation to the median that is asymptotically accurate at high $k$ and reasonable down to $k = 0.5$ or a bit lower follows from the Wilson–Hilferty transformation:
: $\nu(k) = k \left( 1 - \frac \right)^3$
which goes negative for $k < 1/9$.

In 2021, Lyon proposed several closed-form approximations of the form $\nu(k) \approx 2^(A + Bk)$. He conjectured closed-form values of $A$ and $B$ for which this approximation is an asymptotically tight upper or lower bound for all $k > 0$. In particular:

: $\nu_(k) = 2^(\log 2 - \frac + k) \quad$ is a lower bound, asymptotically tight as $k \to \infty$
: $\nu_U(k) = 2^(e^ + k) \quad$ is an upper bound, asymptotically tight as $k \to 0$

Lyon also derived two other lower bounds that are not closed-form expressions, including this one based on solving the integral expression substituting 1 for $e^$:
:$\nu(k) > \left( \frac \right)^ \quad$ (approaching equality as $k \to 0$)
and the tangent line at $k = 1$ where the derivative was found to be $\nu^\prime(1) \approx 0.9680448$:
:$\nu(k) \ge \nu(1) + (k-1) \nu^\prime(1) \quad$ (with equality at $k = 1$)
:$\nu(k) \ge \log(2) + (k-1) (\gamma - 2 \operatorname(-\log 2) - \log \log 2)$
where Ei is the exponential integral.

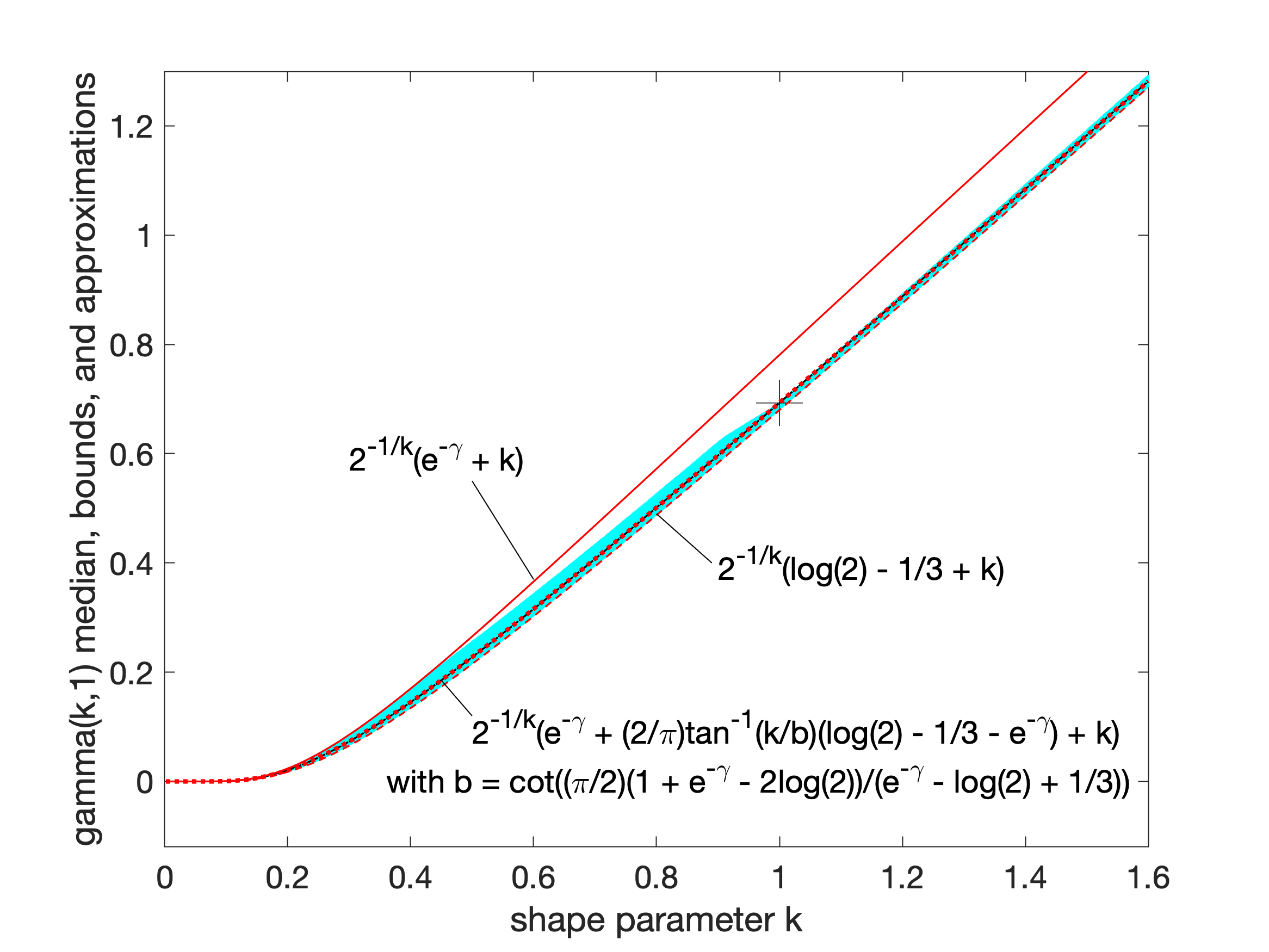
Additionally, he showed that interpolations between bounds could provide excellent approximations or tighter bounds to the median, including an approximation that is exact at $k = 1$ (where $\nu(1) = \log 2$) and has a maximum relative error less than 0.6%. Interpolated approximations and bounds are all of the form
:$\nu(k) \approx \tilde(k)\nu_(k) + (1 - \tilde(k))\nu_U(k)$
where $\tilde$ is an interpolating function running monotonically from 0 at low $k$ to 1 at high $k$, approximating an ideal, or exact, interpolator $g(k)$:
:$g(k) = \frac$
For the simplest interpolating function considered, a first-order rational function
:$\tilde_1(k) = \frac$
the tightest lower bound has
:$b_0 = \frac - \log 2 \approx 0.143472$
and the tightest upper bound has
:$b_0 = \frac \approx 0.374654$
The interpolated bounds are plotted (mostly inside the yellow region) in the log–log plot shown. Even tighter bounds are available using different interpolating functions, but not usually with closed-form parameters like these.

Summation

If ''X''_''i'' has a Gamma(''k''_''i'', ''θ'') distribution for ''i'' = 1, 2, ..., ''N'' (i.e., all distributions have the same scale parameter ''θ''), then

:$\sum_^N X_i \sim\mathrm \left( \sum_^N k_i, \theta \right)$

provided all ''X''_''i'' are independent.

For the cases where the ''X''_''i'' are independent but have different scale parameters, see Mathai or Moschopoulos.

The gamma distribution exhibits infinite divisibility.

Scaling

If
: $X \sim \mathrm(k, \theta),$

then, for any ''c'' > 0,

: $cX \sim \mathrm(k, c\,\theta),$ by moment generating functions,

or equivalently, if

: $X \sim \mathrm\left( \alpha,\beta \right)$ (shape-rate parameterization)

: $cX \sim \mathrm\left( \alpha, \frac \beta c \right),$

Indeed, we know that if ''X'' is an exponential r.v. with rate ''λ'', then ''cX'' is an exponential r.v. with rate ''λ''/''c''; the same thing is valid with Gamma variates (and this can be checked using the moment-generating function, see, e.g
these notes
10.4-(ii)): multiplication by a positive constant ''c'' divides the rate (or, equivalently, multiplies the scale).

Exponential family

The gamma distribution is a two-parameter exponential family with natural parameters ''k'' âˆ’ 1 and −1/''θ'' (equivalently, ''α'' âˆ’ 1 and −''β''), and natural statistics ''X'' and ln(''X'').

If the shape parameter ''k'' is held fixed, the resulting one-parameter family of distributions is a natural exponential family.

Logarithmic expectation and variance

One can show that

: \operatorname ln(X)= \psi(\alpha) - \ln(\beta)

or equivalently,

: \operatorname ln(X)= \psi(k) + \ln(\theta)

where $\psi$ is the digamma function. Likewise,

: \operatorname ln(X)= \psi^(\alpha) = \psi^(k)

where $\psi^$ is the trigamma function.

This can be derived using the exponential family formula for the moment generating function of the sufficient statistic, because one of the sufficient statistics of the gamma distribution is ln(''x'').

Information entropy

The information entropy is

:
\begin
\operatorname(X) & = \operatorname \ln(p(X))\\ pt& = \operatorname \alpha \ln(\beta) + \ln(\Gamma(\alpha)) - (\alpha-1)\ln(X) + \beta X\\ pt& = \alpha - \ln(\beta) + \ln(\Gamma(\alpha)) + (1-\alpha)\psi(\alpha).
\end

In the ''k'', ''θ'' parameterization, the information entropy is given by

: $\operatorname(X) =k + \ln(\theta) + \ln(\Gamma(k)) + (1-k)\psi(k).$

Kullback–Leibler divergence

The Kullback–Leibler divergence (KL-divergence), of Gamma(''α''_''p'', ''β''_''p'') ("true" distribution) from Gamma(''α''_''q'', ''β''_''q'') ("approximating" distribution) is given by

: $\begin D_(\alpha_p,\beta_p; \alpha_q, \beta_q) = & (\alpha_p-\alpha_q) \psi(\alpha_p) - \log\Gamma(\alpha_p) + \log\Gamma(\alpha_q) \\ & + \alpha_q(\log \beta_p - \log \beta_q) + \alpha_p\frac. \end$

Written using the ''k'', ''θ'' parameterization, the KL-divergence of Gamma(''k_p'', θ_''p'') from Gamma(''k_q'', ''θ''_''q'') is given by

: $\begin D_(k_p,\theta_p; k_q, \theta_q) = & (k_p-k_q)\psi(k_p) - \log\Gamma(k_p) + \log\Gamma(k_q) \\ & + k_q(\log \theta_q - \log \theta_p) + k_p \frac. \end$

Laplace transform

The Laplace transform of the gamma PDF is

:$F(s) = (1 + \theta s)^ = \frac .$

Related distributions

General

* Let $X_1, X_2, \ldots, X_n$ be $n$ independent and identically distributed random variables following an exponential distribution with rate parameter λ, then $\sum_i X_i$ ~ Gamma(n, λ) where n is the shape parameter and ''λ'' is the rate, and $\bar = \frac \sum_i X_i \sim \operatorname(n, n\lambda)$ where the rate changes ''nλ''.
* If ''X'' ~ Gamma(1, 1/''λ'') (in the shape–scale parametrization), then ''X'' has an exponential distribution with rate parameter ''λ''.
* If ''X'' ~ Gamma(''ν''/2, 2) (in the shape–scale parametrization), then ''X'' is identical to ''χ''²(''ν''), the chi-squared distribution with ''ν'' degrees of freedom. Conversely, if ''Q'' ~ ''χ''²(''ν'') and ''c'' is a positive constant, then ''cQ'' ~ Gamma(''ν''/2, 2''c'').
* If ''k'' is an integer, the gamma distribution is an Erlang distribution and is the probability distribution of the waiting time until the ''k''th "arrival" in a one-dimensional Poisson process with intensity 1/''θ''. If
::$X \sim \Gamma(k \in \mathbf, \theta), \qquad Y \sim \operatorname\left(\frac x \theta \right),$
:then
::$P(X > x) = P(Y < k).$
* If ''X'' has a Maxwell–Boltzmann distribution with parameter ''a'', then
::$X^2 \sim \Gamma\left(\frac, 2a^2\right).$

* If ''X'' ~ Gamma(''k'', ''θ''), then $\log X$ follows an exponential-gamma (abbreviated exp-gamma) distribution. It is sometimes referred to as the log-gamma distribution. Formulas for its mean and variance are in the section #Logarithmic expectation and variance.
* If ''X'' ~ Gamma(''k'', ''θ''), then $\sqrt$ follows a generalized gamma distribution with parameters ''p'' = 2, ''d'' = 2''k'', and $a = \sqrt$ .
* More generally, if ''X'' ~ Gamma(''k'',''θ''), then $X^q$ for $q > 0$ follows a generalized gamma distribution with parameters ''p'' = 1/''q'', ''d'' = ''k''/''q'', and $a = \theta^q$.
* If ''X'' ~ Gamma(''k'', ''θ'') with shape ''k'' and scale ''θ'', then 1/''X'' ~ Inv-Gamma(''k'', ''θ''^−1) (see Inverse-gamma distribution for derivation).
*Parametrization 1: If $X_k \sim \Gamma(\alpha_k,\theta_k)\,$ are independent, then $\frac \sim \mathrm(2\alpha_1, 2\alpha_2)$, or equivalently, $\frac \sim \beta'\left(\alpha_1, \alpha_2, 1, \frac\right)$
*Parametrization 2: If $X_k \sim \Gamma(\alpha_k,\beta_k)\,$ are independent, then $\frac \sim \mathrm(2\alpha_1, 2\alpha_2)$, or equivalently, $\frac \sim \beta'\left(\alpha_1, \alpha_2, 1, \frac\right)$
* If ''X'' ~ Gamma(''α'', ''θ'') and ''Y'' ~ Gamma(''β'', ''θ'') are independently distributed, then ''X''/(''X'' + ''Y'') has a beta distribution with parameters ''α'' and ''β'', and ''X''/(''X'' + ''Y'') is independent of ''X'' + ''Y'', which is Gamma(''α'' + ''β'', ''θ'')-distributed.
* If ''X''_''i'' ~ Gamma(''α''_''i'', 1) are independently distributed, then the vector (''X''₁/''S'', ..., ''X_n''/''S''), where ''S'' = ''X''₁ + ... + ''X_n'', follows a Dirichlet distribution with parameters ''α''₁, ..., ''α''_''n''.
* For large ''k'' the gamma distribution converges to normal distribution with mean ''μ'' = ''kθ'' and variance ''σ''² = ''kθ''².
* The gamma distribution is the conjugate prior for the precision of the normal distribution with known mean.
* The matrix gamma distribution and the Wishart distribution are multivariate generalizations of the gamma distribution (samples are positive-definite matrices rather than positive real numbers).
* The gamma distribution is a special case of the generalized gamma distribution, the generalized integer gamma distribution, and the generalized inverse Gaussian distribution.
* Among the discrete distributions, the negative binomial distribution is sometimes considered the discrete analog of the gamma distribution.
* Tweedie distributions – the gamma distribution is a member of the family of Tweedie exponential dispersion models.
* Modified Half-normal distribution – the Gamma distribution is a member of the family of Modified half-normal distribution. The corresponding density is $f(x\mid \alpha, \beta, \gamma)= \frac$, where $\Psi(\alpha,z)=_1\Psi_1\left(\begin\left(\alpha,\frac\right)\\(1,0)\end;z \right)$ denotes the Fox-Wright Psi function.

Compound gamma

If the shape parameter of the gamma distribution is known, but the inverse-scale parameter is unknown, then a gamma distribution for the inverse scale forms a conjugate prior. The compound distribution, which results from integrating out the inverse scale, has a closed-form solution known as the compound gamma distribution.

If, instead, the shape parameter is known but the mean is unknown, with the prior of the mean being given by another gamma distribution, then it results in K-distribution.

Weibull and Stable count

The gamma distribution $f(x;k) \, (k > 1)$ can be expressed as the product distribution of a Weibull distribution and a variant form of the stable count distribution.
Its shape parameter $k$ can be regarded as the inverse of Lévy's stability parameter in the stable count distribution:

f(x;k) =
\displaystyle\int_0^\infty \frac \, W_k(\frac)
\left k u^ \, \mathfrak_\left(u^k\right) \right\, du ,

where $\mathfrak_(\nu)$ is a standard stable count distribution of shape $\alpha = 1/k$, and $W_k(x)$ is a standard Weibull distribution of shape $k$.

Statistical inference

Parameter estimation

Maximum likelihood estimation

The likelihood function for ''N'' iid observations (''x''₁, ..., ''x''_''N'') is

:$L(k, \theta) = \prod_^N f(x_i;k,\theta)$

from which we calculate the log-likelihood function

:$\ell(k, \theta) = (k - 1) \sum_^N \ln(x_i) - \sum_^N \frac \theta - Nk\ln(\theta) - N\ln(\Gamma(k))$

Finding the maximum with respect to ''θ'' by taking the derivative and setting it equal to zero yields the maximum likelihood estimator of the ''θ'' parameter, which equals the sample mean $\bar$ divided by the shape parameter ''k'':

:$\hat = \frac\sum_^N x_i = \frac$

Substituting this into the log-likelihood function gives

:$\ell = (k-1)\sum_^N \ln(x_i) -Nk - Nk\ln \left(\frac \right) - N\ln(\Gamma(k))$

Finding the maximum with respect to ''k'' by taking the derivative and setting it equal to zero yields

:$\ln(k) - \psi(k) = \ln\left(\frac\sum_^N x_i\right) - \frac 1 N \sum_^N \ln(x_i) = \ln(\bar) - \overline$

where $\psi$ is the digamma function and $\overline$ is the sample mean of ln(''x''). There is no closed-form solution for ''k''. The function is numerically very well behaved, so if a numerical solution is desired, it can be found using, for example, Newton's method. An initial value of ''k'' can be found either using the method of moments, or using the approximation

:$\ln(k) - \psi(k) \approx \frac\left(1 + \frac\right)$

If we let

:$s = \ln \left(\frac 1 N \sum_^N x_i\right) - \frac 1 N \sum_^N \ln (x_i) = \ln(\bar) - \overline$

then ''k'' is approximately

: $k \approx \frac$

which is within 1.5% of the correct value. An explicit form for the Newton–Raphson update of this initial guess is:

:$k \leftarrow k - \frac.$

Closed-form estimators

Consistent closed-form estimators of ''k'' and ''θ'' exists that are derived from the likelihood of the generalized gamma distribution.

The estimate for the shape ''k'' is

: $\hat = \frac$

and the estimate for the scale ''θ'' is

: $\hat = \frac \left(N \sum_^N x_i \ln(x_i) - \sum_^N x_i \sum_^N \ln(x_i)\right)$

Using the sample mean of ''x'', the sample mean of ln(''x''), and the sample mean of the product ''x''·ln(''x'') simplifies the expressions to:

: $\hat = \bar / \hat$
: $\hat = \overline - \bar \overline.$

If the rate parameterization is used, the estimate of $\hat = 1/\hat$.

These estimators are not strictly maximum likelihood estimators, but are instead referred to as mixed type log-moment estimators. They have however similar efficiency as the maximum likelihood estimators.

Although these estimators are consistent, they have a small bias. A bias-corrected variant of the estimator for the scale ''θ'' is

: $\tilde = \frac \hat$

A bias correction for the shape parameter ''k'' is given as

: $\tilde = \hat - \frac \left(3 \hat - \frac \left(\frac\right) - \frac \frac \right)$

Bayesian minimum mean squared error

With known ''k'' and unknown ''θ'', the posterior density function for theta (using the standard scale-invariant prior for ''θ'') is

: $P(\theta \mid k, x_1, \dots, x_N) \propto \frac 1 \theta \prod_^N f(x_i; k, \theta)$

Denoting

:$y \equiv \sum_^Nx_i , \qquad P(\theta \mid k, x_1, \dots, x_N) = C(x_i) \theta^ e^$

Integration with respect to ''θ'' can be carried out using a change of variables, revealing that 1/''θ'' is gamma-distributed with parameters ''α'' = ''Nk'', ''β'' = ''y''.

:$\int_0^\infty \theta^ e^\, d\theta = \int_0^\infty x^ e^ \, dx = y^ \Gamma(Nk - m) \!$

The moments can be computed by taking the ratio (''m'' by ''m'' = 0)

: \operatorname ^m= \frac y^m

which shows that the mean ± standard deviation estimate of the posterior distribution for ''θ'' is

:$\frac y \pm \sqrt.$

Bayesian inference

Conjugate prior

In Bayesian inference, the gamma distribution is the conjugate prior to many likelihood distributions: the Poisson, exponential, normal (with known mean), Pareto, gamma with known shape ''σ'', inverse gamma with known shape parameter, and Gompertz with known scale parameter.

The gamma distribution's conjugate prior is:Fink, D. 199
A Compendium of Conjugate Priors
In progress report: Extension and enhancement of methods for setting data quality objectives. (DOE contract 95‑831).

: $p(k,\theta \mid p, q, r, s) = \frac \frac,$

where ''Z'' is the normalizing constant with no closed-form solution.
The posterior distribution can be found by updating the parameters as follows:

:$\begin p' &= p\prod\nolimits_i x_i,\\ q' &= q + \sum\nolimits_i x_i,\\ r' &= r + n,\\ s' &= s + n, \end$

where ''n'' is the number of observations, and ''x_i'' is the ''i''th observation.

Occurrence and applications

Consider a sequence of events, with the waiting time for each event being an exponential distribution with rate $\beta$. Then the waiting time for the $n$-th event to occur is the gamma distribution with integer shape $\alpha = n$. This construction of the gamma distribution allows it to model a wide variety of phenomena where several sub-events, each taking time with exponential distribution, must happen in sequence for a major event to occur. Examples include the waiting time of cell-division events, number of compensatory mutations for a given mutation, waiting time until a repair is necessary for a hydraulic system, and so on.

The gamma distribution has been used to model the size of insurance claims and rainfalls. This means that aggregate insurance claims and the amount of rainfall accumulated in a reservoir are modelled by a gamma process – much like the exponential distribution generates a Poisson process.

The gamma distribution is also used to model errors in multi-level Poisson regression models because a mixture of Poisson distributions with gamma-distributed rates has a known closed form distribution, called negative binomial.

In wireless communication, the gamma distribution is used to model the multi-path fading of signal power; see also Rayleigh distribution and Rician distribution.

In oncology, the age distribution of cancer incidence often follows the gamma distribution, wherein the shape and scale parameters predict, respectively, the number of driver events and the time interval between them.

In neuroscience, the gamma distribution is often used to describe the distribution of inter-spike intervals.J. G. Robson and J. B. Troy, "Nature of the maintained discharge of Q, X, and Y retinal ganglion cells of the cat", J. Opt. Soc. Am. A 4, 2301–2307 (1987)M.C.M. Wright, I.M. Winter, J.J. Forster, S. Bleeck "Response to best-frequency tone bursts in the ventral cochlear nucleus is governed by ordered inter-spike interval statistics", Hearing Research 317 (2014)

In bacterial gene expression, the copy number of a constitutively expressed protein often follows the gamma distribution, where the scale and shape parameter are, respectively, the mean number of bursts per cell cycle and the mean number of protein molecules produced by a single mRNA during its lifetime.N. Friedman, L. Cai and X. S. Xie (2006) "Linking stochastic dynamics to population distribution: An analytical framework of gene expression", ''Phys. Rev. Lett.'' 97, 168302.

In genomics, the gamma distribution was applied in peak calling step (i.e., in recognition of signal) in ChIP-chipDJ Reiss, MT Facciotti and NS Baliga (2008
"Model-based deconvolution of genome-wide DNA binding"
''Bioinformatics'', 24, 396–403 and ChIP-seqMA Mendoza-Parra, M Nowicka, W Van Gool, H Gronemeyer (2013
"Characterising ChIP-seq binding patterns by model-based peak shape deconvolution"
''BMC Genomics'', 14:834 data analysis.

In Bayesian statistics, the gamma distribution is widely used as a conjugate prior. It is the conjugate prior for the precision (i.e. inverse of the variance) of a normal distribution. It is also the conjugate prior for the exponential distribution.

Random variate generation

Given the scaling property above, it is enough to generate gamma variables with ''θ'' = 1, as we can later convert to any value of ''β'' with a simple division.

Suppose we wish to generate random variables from Gamma(''n'' + ''δ'', 1), where n is a non-negative integer and 0 < ''δ'' < 1. Using the fact that a Gamma(1, 1) distribution is the same as an Exp(1) distribution, and noting the method of generating exponential variables, we conclude that if ''U'' is uniformly distributed on (0, 1], then −ln(''U'') is distributed Gamma(1, 1) (i.e. inverse transform sampling). Now, using the "''α''-addition" property of gamma distribution, we expand this result:

: $-\sum_^n \ln U_k \sim \Gamma(n, 1)$

where ''U''_''k'' are all uniformly distributed on (0, 1] and independent. All that is left now is to generate a variable distributed as Gamma(''δ'', 1) for 0 < ''δ'' < 1 and apply the "''α''-addition" property once more. This is the most difficult part.

Random generation of gamma variates is discussed in detail by Devroye, See Chapter 9, Section 3. noting that none are uniformly fast for all shape parameters. For small values of the shape parameter, the algorithms are often not valid. For arbitrary values of the shape parameter, one can apply the Ahrens and Dieter. See Algorithm GD, p. 53. modified acceptance-rejection method Algorithm GD (shape ''k'' ≥ 1), or transformation method when 0 < ''k'' < 1. Also see Cheng and Feast Algorithm GKM 3 or Marsaglia's squeeze method.

The following is a version of the Ahrens-Dieter rejection sampling, acceptance–rejection method:

# Generate ''U'', ''V'' and ''W'' as iid uniform (0, 1] variates.
# If $U\le\frac e$ then $\xi=V^$ and $\eta=W\xi^$. Otherwise, $\xi=1-\ln V$ and $\eta=We^$.
# If $\eta>\xi^e^$ then go to step 1.
# ''ξ'' is distributed as Γ(''δ'', 1).

A summary of this is
: $\theta \left( \xi - \sum_^ \ln(U_i) \right) \sim \Gamma (k, \theta)$
where $\scriptstyle \lfloor k \rfloor$ is the integer part of ''k'', ''ξ'' is generated via the algorithm above with ''δ'' = (the fractional part of ''k'') and the ''U''_''k'' are all independent.

While the above approach is technically correct, Devroye notes that it is linear in the value of ''k'' and generally is not a good choice. Instead, he recommends using either rejection-based or table-based methods, depending on context.

For example, Marsaglia's simple transformation-rejection method relying on one normal variate ''X'' and one uniform variate ''U'':

# Set $d = a - \frac13$ and $c = \frac1$.
# Set $v=(1+cX)^3$.
# If $v > 0$ and $\ln U < \frac2 + d - dv + d\ln v$ return $dv$, else go back to step 2.

With $1 \le a = \alpha = k$ generates a gamma distributed random number in time that is approximately constant with ''k''. The acceptance rate does depend on ''k'', with an acceptance rate of 0.95, 0.98, and 0.99 for k=1, 2, and 4. For ''k'' < 1, one can use $\gamma_\alpha = \gamma_ U^$ to boost ''k'' to be usable with this method.

References

External links

*
*
* ModelAssist (2017
Uses of the gamma distribution in risk modeling, including applied examples in Excel

{{DEFAULTSORT:Gamma Distribution
Continuous distributions
Factorial and binomial topics
Conjugate prior distributions
Exponential family distributions
Infinitely divisible probability distributions
Survival analysis