Dipole antenna on:
[Wikipedia]
[Google]
[Amazon]


 In
In
 The feedpoint is usually at the center of the dipole as shown in the diagram. The current along dipole arms are approximately described as proportional to where is the distance to the end of the arm. In the case of a short dipole, that is essentially a linear drop from at the feedpoint to zero at the end. Therefore, this is comparable to a Hertzian dipole with an ''effective'' current h equal to the average current over the conductor, so With that substitution, the above equations closely approximate the fields generated by a short dipole fed by current
From the fields calculated above, one can find the radiated ''flux'' (power per unit area) at any point as the magnitude of the real part of the Poynting vector, , which is given by With and being at right angles and in phase, there is no imaginary part and is simply equal to with the phase factors (the exponentials) cancelling out leaving:
:
We have now expressed the flux in terms of the feedpoint current 0 and the ratio of the short dipole's length to the wavelength of radiation . The radiation pattern given by is seen to be similar to and only slightly less directional than that of the half-wave dipole.
The feedpoint is usually at the center of the dipole as shown in the diagram. The current along dipole arms are approximately described as proportional to where is the distance to the end of the arm. In the case of a short dipole, that is essentially a linear drop from at the feedpoint to zero at the end. Therefore, this is comparable to a Hertzian dipole with an ''effective'' current h equal to the average current over the conductor, so With that substitution, the above equations closely approximate the fields generated by a short dipole fed by current
From the fields calculated above, one can find the radiated ''flux'' (power per unit area) at any point as the magnitude of the real part of the Poynting vector, , which is given by With and being at right angles and in phase, there is no imaginary part and is simply equal to with the phase factors (the exponentials) cancelling out leaving:
:
We have now expressed the flux in terms of the feedpoint current 0 and the ratio of the short dipole's length to the wavelength of radiation . The radiation pattern given by is seen to be similar to and only slightly less directional than that of the half-wave dipole.
 Using the above expression for the radiation in the far field for a given feedpoint current, we can integrate over all solid angle to obtain the total radiated power.
:
From that, it is possible to infer the radiation resistance, equal to the resistive (real) part of the feedpoint impedance, neglecting a component due to ohmic losses. By setting total to the power supplied at the feedpoint we find:
:
Again, these become exact for Setting despite its use not quite being valid for so large a fraction of the wavelength, the formula would predict a radiation resistance of 49 Ω, instead of the actual value of 73 Ω produced by a half-wave dipole when more correct quarter-wave sinusoidal currents are used.
Using the above expression for the radiation in the far field for a given feedpoint current, we can integrate over all solid angle to obtain the total radiated power.
:
From that, it is possible to infer the radiation resistance, equal to the resistive (real) part of the feedpoint impedance, neglecting a component due to ohmic losses. By setting total to the power supplied at the feedpoint we find:
:
Again, these become exact for Setting despite its use not quite being valid for so large a fraction of the wavelength, the formula would predict a radiation resistance of 49 Ω, instead of the actual value of 73 Ω produced by a half-wave dipole when more correct quarter-wave sinusoidal currents are used.
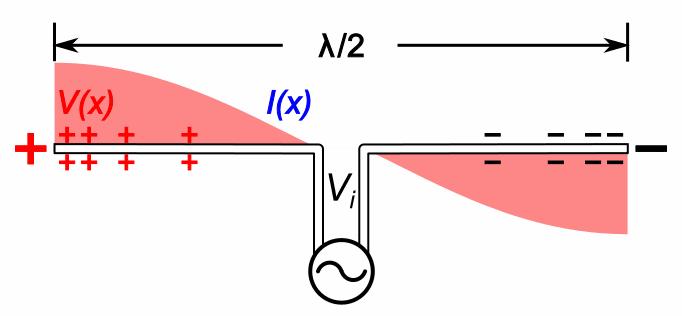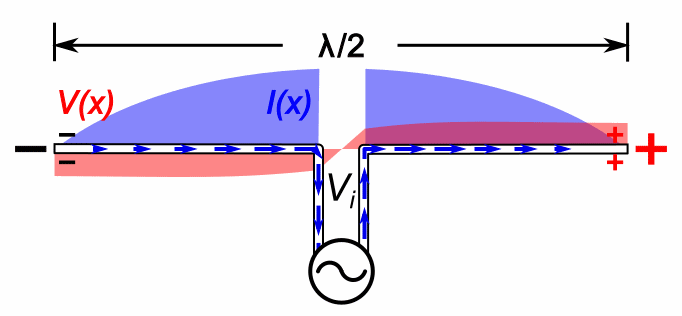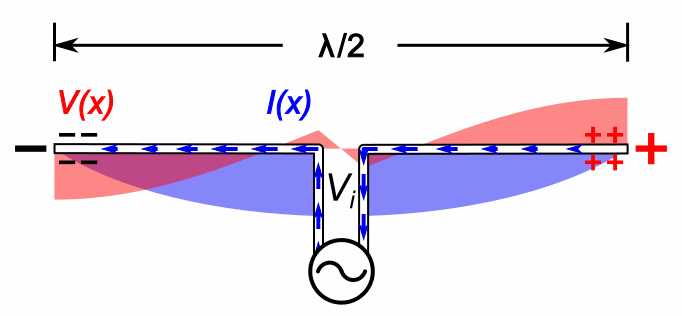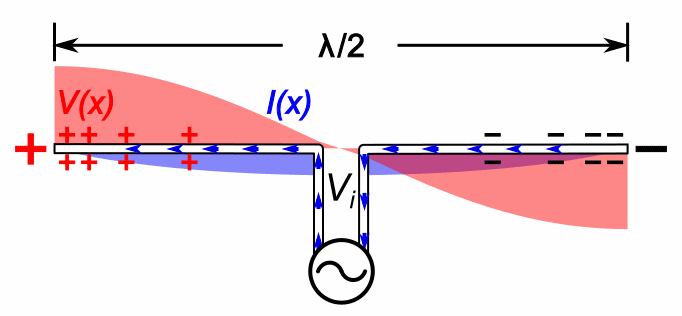 A half-wave dipole antenna consists of two quarter-wavelength conductors placed end to end for a total length of approximately ''L'' = λ/2. The current distribution is that of a
A half-wave dipole antenna consists of two quarter-wavelength conductors placed end to end for a total length of approximately ''L'' = λ/2. The current distribution is that of a
 * The '' cage dipole'' is a similar modification in which the bandwidth is increased by using fat cylindrical dipole elements made of a "cage" of wires (see photo). These are used in a few broadband array antennas in the medium wave and shortwave bands for applications such as over-the-horizon radar and radio telescopes.
* A '' halo antenna'' is a half-wave dipole bent into a circle for a nearly uniform radiation pattern in the plane of the circle. When the halo's circle is horizontal, it produces horizontally polarized radiation in a nearly omnidirectional pattern with little power wasted toward the sky, compared to a straight horizontal dipole. In practice, it is categorized both as a bent dipole and as a loop antenna, depending on author preference.
* A '' turnstile antenna'' comprises two dipoles crossed at a right angle and feed system which introduces a quarter-wave phase difference between the currents along the two. With that geometry, the two dipoles do not interact electrically but their fields add in the far-field producing a net radiation pattern which is rather close to
* The '' cage dipole'' is a similar modification in which the bandwidth is increased by using fat cylindrical dipole elements made of a "cage" of wires (see photo). These are used in a few broadband array antennas in the medium wave and shortwave bands for applications such as over-the-horizon radar and radio telescopes.
* A '' halo antenna'' is a half-wave dipole bent into a circle for a nearly uniform radiation pattern in the plane of the circle. When the halo's circle is horizontal, it produces horizontally polarized radiation in a nearly omnidirectional pattern with little power wasted toward the sky, compared to a straight horizontal dipole. In practice, it is categorized both as a bent dipole and as a loop antenna, depending on author preference.
* A '' turnstile antenna'' comprises two dipoles crossed at a right angle and feed system which introduces a quarter-wave phase difference between the currents along the two. With that geometry, the two dipoles do not interact electrically but their fields add in the far-field producing a net radiation pattern which is rather close to
 The "vertical", "Marconi", or monopole antenna is a single-element antenna usually fed at the bottom (with the shield side of its unbalanced transmission line connected to ground). It behaves essentially as a dipole antenna. The ground (or ground plane) is considered to be a conductive surface which works as a reflector (see effect of ground). Vertical currents in the reflected image have the same direction (thus are ''not'' reflected about the ground) and phase as the current in the real antenna. The conductor and its image together act as a dipole in the upper half of space. Like a dipole, in order to achieve resonance (resistive feedpoint impedance) the conductor must be close to a quarter wavelength in height (like each conductor in a half-wave dipole).
In this upper side of space, the emitted field has the same amplitude of the field radiated by a similar dipole fed with the same current. Therefore, the total emitted power is half the emitted power of a dipole fed with the same current. As the current is the same, the radiation resistance (real part of series impedance) will be half of the series impedance of the comparable dipole. A quarter-wave monopole, then, has an impedance of Ω. Another way of seeing this, is that a true dipole receiving a current I has voltages on its terminals of +V and −V, for an impedance across the terminals of 2V/I, whereas the comparable vertical antenna has the current I but an applied voltage of only V.
Since the fields above ground are the same as for the dipole, but only half the power is applied, the gain is doubled to 5.14 dBi. This is not an actual performance advantage per se, since in practice a dipole also reflects half of its power off the ground which (depending on the antenna height and sky angle) can augment (or cancel!) the direct signal. The vertical polarization of the monopole (as for a vertically oriented dipole) is advantageous at low elevation angles where the ground reflection combines with the direct wave approximately in phase.
The earth acts as a ground plane, but it can be a poor conductor leading to losses. Its conductivity can be improved (at cost) by laying a copper mesh. When an actual ground is not available (such as in a vehicle) other metallic surfaces can serve as a ground plane (typically the vehicle's roof). Alternatively, radial wires placed at the base of the antenna can form a ground plane. For VHF and UHF bands, the radiating and ground plane elements can be constructed from rigid rods or tubes. Using such an artificial ground plane allows for the entire antenna and "ground" to be mounted at an arbitrary height. One common modification has the radials forming the ground plane sloped down, which has the effect of raising the feedpoint impedance to around 50 Ω, matching common coaxial cable. No longer being a true ground, a balun (such as a simple choke balun) is then recommended.
The "vertical", "Marconi", or monopole antenna is a single-element antenna usually fed at the bottom (with the shield side of its unbalanced transmission line connected to ground). It behaves essentially as a dipole antenna. The ground (or ground plane) is considered to be a conductive surface which works as a reflector (see effect of ground). Vertical currents in the reflected image have the same direction (thus are ''not'' reflected about the ground) and phase as the current in the real antenna. The conductor and its image together act as a dipole in the upper half of space. Like a dipole, in order to achieve resonance (resistive feedpoint impedance) the conductor must be close to a quarter wavelength in height (like each conductor in a half-wave dipole).
In this upper side of space, the emitted field has the same amplitude of the field radiated by a similar dipole fed with the same current. Therefore, the total emitted power is half the emitted power of a dipole fed with the same current. As the current is the same, the radiation resistance (real part of series impedance) will be half of the series impedance of the comparable dipole. A quarter-wave monopole, then, has an impedance of Ω. Another way of seeing this, is that a true dipole receiving a current I has voltages on its terminals of +V and −V, for an impedance across the terminals of 2V/I, whereas the comparable vertical antenna has the current I but an applied voltage of only V.
Since the fields above ground are the same as for the dipole, but only half the power is applied, the gain is doubled to 5.14 dBi. This is not an actual performance advantage per se, since in practice a dipole also reflects half of its power off the ground which (depending on the antenna height and sky angle) can augment (or cancel!) the direct signal. The vertical polarization of the monopole (as for a vertically oriented dipole) is advantageous at low elevation angles where the ground reflection combines with the direct wave approximately in phase.
The earth acts as a ground plane, but it can be a poor conductor leading to losses. Its conductivity can be improved (at cost) by laying a copper mesh. When an actual ground is not available (such as in a vehicle) other metallic surfaces can serve as a ground plane (typically the vehicle's roof). Alternatively, radial wires placed at the base of the antenna can form a ground plane. For VHF and UHF bands, the radiating and ground plane elements can be constructed from rigid rods or tubes. Using such an artificial ground plane allows for the entire antenna and "ground" to be mounted at an arbitrary height. One common modification has the radials forming the ground plane sloped down, which has the effect of raising the feedpoint impedance to around 50 Ω, matching common coaxial cable. No longer being a true ground, a balun (such as a simple choke balun) is then recommended.
 The feedpoint impedance of a dipole antenna is sensitive to its electrical length and feedpoint position. Therefore, a dipole will generally only perform optimally over a rather narrow bandwidth, beyond which its impedance will become a poor match for the transmitter or receiver (and transmission line). The real (resistive) and imaginary (reactive) components of that impedance, as a function of electrical length, are shown in the accompanying graph. The detailed calculation of these numbers are described
The feedpoint impedance of a dipole antenna is sensitive to its electrical length and feedpoint position. Therefore, a dipole will generally only perform optimally over a rather narrow bandwidth, beyond which its impedance will become a poor match for the transmitter or receiver (and transmission line). The real (resistive) and imaginary (reactive) components of that impedance, as a function of electrical length, are shown in the accompanying graph. The detailed calculation of these numbers are described  A true half-wave dipole is one half of the wavelength λ in length, where in free space. Such a dipole has a feedpoint impedance consisting of 73Ω resistance and +43Ω reactance, thus presenting a slightly inductive reactance. To cancel that reactance, and present a pure resistance to the feedline, the element is shortened by the factor ''k'' for a net length '''' of:
:
where ''λ'' is the free-space wavelength, ''c'' is the
A true half-wave dipole is one half of the wavelength λ in length, where in free space. Such a dipole has a feedpoint impedance consisting of 73Ω resistance and +43Ω reactance, thus presenting a slightly inductive reactance. To cancel that reactance, and present a pure resistance to the feedline, the element is shortened by the factor ''k'' for a net length '''' of:
:
where ''λ'' is the free-space wavelength, ''c'' is the  For a typical ''k'' of about 0.95, the above formula for the corrected antenna length can be written, for a length in metres as 143/''f'', or a length in feet as 468/''f'' where ''f'' is the frequency in megahertz.
Dipole antennas of lengths approximately equal to any ''odd'' multiple of λ are also resonant, presenting a small reactance (which can be cancelled by a small length adjustment). However these are rarely used. One size that is more practical though is a dipole with a length of wavelengths. Not being close to wavelengths, this antenna's impedance has a large (negative) reactance and can only be used with an impedance matching network (a so-called
For a typical ''k'' of about 0.95, the above formula for the corrected antenna length can be written, for a length in metres as 143/''f'', or a length in feet as 468/''f'' where ''f'' is the frequency in megahertz.
Dipole antennas of lengths approximately equal to any ''odd'' multiple of λ are also resonant, presenting a small reactance (which can be cancelled by a small length adjustment). However these are rarely used. One size that is more practical though is a dipole with a length of wavelengths. Not being close to wavelengths, this antenna's impedance has a large (negative) reactance and can only be used with an impedance matching network (a so-called
 One of the most common applications of the dipole antenna is the ''rabbit ears'' or ''bunny ears'' television antenna, found atop broadcast television receivers. It is used to receive the VHF terrestrial television bands, consisting in the US of 54 to 88 MHz ( band I) and 174 to 216 MHz ( band III), with wavelengths of 5.5 to 1.4 m. Since this frequency range is much wider than a single fixed dipole antenna can cover, it is made with several degrees of adjustment. It is constructed of two telescoping rods that can each be extended out to about 1 m length (one quarter wavelength at 75 MHz). With control over the segments' length, angle with respect to vertical, and compass angle, one has much more flexibility in optimizing reception than available with a rooftop antenna even if equipped with an
One of the most common applications of the dipole antenna is the ''rabbit ears'' or ''bunny ears'' television antenna, found atop broadcast television receivers. It is used to receive the VHF terrestrial television bands, consisting in the US of 54 to 88 MHz ( band I) and 174 to 216 MHz ( band III), with wavelengths of 5.5 to 1.4 m. Since this frequency range is much wider than a single fixed dipole antenna can cover, it is made with several degrees of adjustment. It is constructed of two telescoping rods that can each be extended out to about 1 m length (one quarter wavelength at 75 MHz). With control over the segments' length, angle with respect to vertical, and compass angle, one has much more flexibility in optimizing reception than available with a rooftop antenna even if equipped with an
 Many types of array antennas are constructed using multiple dipoles, usually half-wave dipoles. The purpose of using multiple dipoles is to increase the directional
Many types of array antennas are constructed using multiple dipoles, usually half-wave dipoles. The purpose of using multiple dipoles is to increase the directional  On the other hand, for a rotating antenna (or one used only towards a particular direction) one may desire increased gain and directivity in a particular horizontal direction. If the broadside array discussed above (whether collinear or not) is turned horizontal, then the one obtains a greater gain in the horizontal direction perpendicular to the antennas, at the expense of most other directions. Unfortunately that also means that the direction ''opposite'' the desired direction also has a high gain, whereas high gain is usually desired in one single direction. The power which is wasted in the reverse direction, however, can be redirected, for instance by using a large planar reflector, as is accomplished in the reflective array antenna, increasing the gain in the desired direction by another 3 dB
An alternative realization of a uni-directional antenna is the ''end-fire array''. In this case the dipoles are again side by side (but not collinear), but fed in progressing phases, arranged so that their waves add coherently in one direction but cancel in the opposite direction. So now, rather than being perpendicular to the array direction as in a broadside array, the directivity is ''in'' the array direction (i.e. the direction of the line connecting their feedpoints) but with one of the opposite directions suppressed.
On the other hand, for a rotating antenna (or one used only towards a particular direction) one may desire increased gain and directivity in a particular horizontal direction. If the broadside array discussed above (whether collinear or not) is turned horizontal, then the one obtains a greater gain in the horizontal direction perpendicular to the antennas, at the expense of most other directions. Unfortunately that also means that the direction ''opposite'' the desired direction also has a high gain, whereas high gain is usually desired in one single direction. The power which is wasted in the reverse direction, however, can be redirected, for instance by using a large planar reflector, as is accomplished in the reflective array antenna, increasing the gain in the desired direction by another 3 dB
An alternative realization of a uni-directional antenna is the ''end-fire array''. In this case the dipoles are again side by side (but not collinear), but fed in progressing phases, arranged so that their waves add coherently in one direction but cancel in the opposite direction. So now, rather than being perpendicular to the array direction as in a broadside array, the directivity is ''in'' the array direction (i.e. the direction of the line connecting their feedpoints) but with one of the opposite directions suppressed.
 The ''Hertzian dipole'' or ''elementary doublet'' refers to a theoretical construction, rather than a physical antenna design: It is an idealized tiny segment of conductor carrying a RF current with constant amplitude and direction along its entire (short) length; a real antenna can be modeled as the combination of many Hertzian dipoles laid end-to-end.
The Hertzian dipole may be defined as a finite oscillating current (in a specified direction) of over a tiny or infinitesimal length at a specified position. The solution of the fields from a Hertzian dipole can be used as the basis for analytical or numerical calculation of the radiation from more complex antenna geometries (such as practical dipoles) by forming the superposition of fields from a large number of Hertzian dipoles comprising the current pattern of the actual antenna. As a function of position, taking the elementary current elements multiplied by infinitesimal lengths , the resulting field pattern then reduces to an
The ''Hertzian dipole'' or ''elementary doublet'' refers to a theoretical construction, rather than a physical antenna design: It is an idealized tiny segment of conductor carrying a RF current with constant amplitude and direction along its entire (short) length; a real antenna can be modeled as the combination of many Hertzian dipoles laid end-to-end.
The Hertzian dipole may be defined as a finite oscillating current (in a specified direction) of over a tiny or infinitesimal length at a specified position. The solution of the fields from a Hertzian dipole can be used as the basis for analytical or numerical calculation of the radiation from more complex antenna geometries (such as practical dipoles) by forming the superposition of fields from a large number of Hertzian dipoles comprising the current pattern of the actual antenna. As a function of position, taking the elementary current elements multiplied by infinitesimal lengths , the resulting field pattern then reduces to an  The far field pattern is thus seen to consist of a transverse electromagnetic (TEM) wave, with electric and magnetic fields at right angles to each other and at right angles to the direction of propagation (the direction of , as we assumed the source to be at the origin). The electric polarization, in the direction, is coplanar with the source current (in the direction), while the magnetic field is at right angles to that, in the direction. It can be seen from these equations, and also in the animation, that the fields at these distances are exactly ''in phase''. Both fields fall according to , with the power thus falling according to as dictated by the inverse square law.
The far field pattern is thus seen to consist of a transverse electromagnetic (TEM) wave, with electric and magnetic fields at right angles to each other and at right angles to the direction of propagation (the direction of , as we assumed the source to be at the origin). The electric polarization, in the direction, is coplanar with the source current (in the direction), while the magnetic field is at right angles to that, in the direction. It can be seen from these equations, and also in the animation, that the fields at these distances are exactly ''in phase''. Both fields fall according to , with the power thus falling according to as dictated by the inverse square law.
Electromagnetic Waves and Antennas
Electromagnetic Waves and Antennas, Sophocles J. Orfanidis.
Wire Antenna Resources including off center fed dipole (OCFD), dipole calculators and construction sites
Wayback Machine
*https://web.archive.org/web/20070926195106/http://www.nt.hs-bremen.de/peik/asc/asc_antenna_slides.pdf
* *
Jed Z. Buchwald, MIT and the Dibner Institute for the History of Science and Technology (link inactive February 2, 2007; archive accessed from Wayback, March 13, 2011)
AC6V's Homebrew Antennas LinksYour First HF Dipole
- simple yet complete tutorial from eham.net
Dipole articles
- s series of pages about the dipole in its various forms {{Authority control Antennas (radio) Heinrich Hertz Radio frequency antenna types Radio technology Articles containing video clips


 In
In radio
Radio is the technology of signaling and communicating using radio waves. Radio waves are electromagnetic waves of frequency between 30 hertz (Hz) and 300 gigahertz (GHz). They are generated by an electronic device called a tr ...
and telecommunications
Telecommunication is the transmission of information by various types of technologies over wire, radio, optical, or other electromagnetic systems. It has its origin in the desire of humans for communication over a distance greater than that ...
a dipole antenna or doublet is the simplest and most widely used class of antenna
Antenna ( antennas or antennae) may refer to:
Science and engineering
* Antenna (radio), also known as an aerial, a transducer designed to transmit or receive electromagnetic (e.g., TV or radio) waves
* Antennae Galaxies, the name of two collid ...
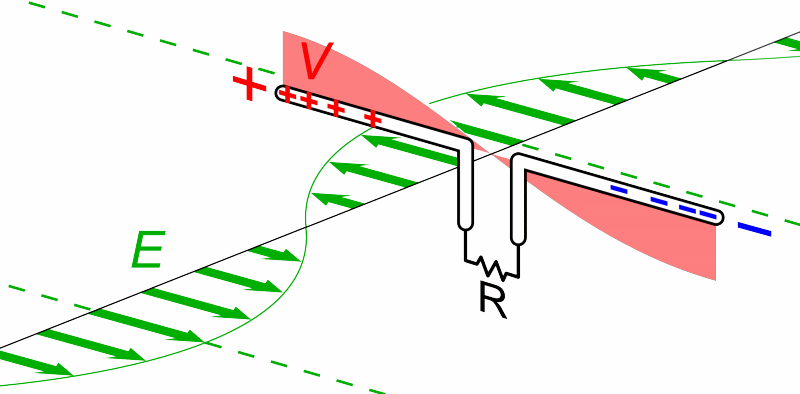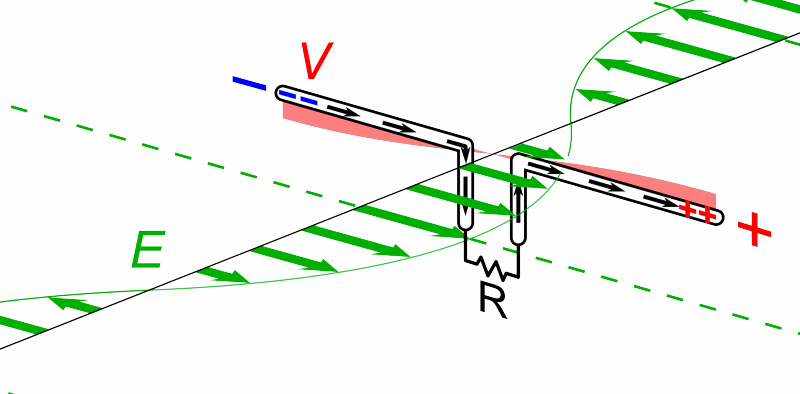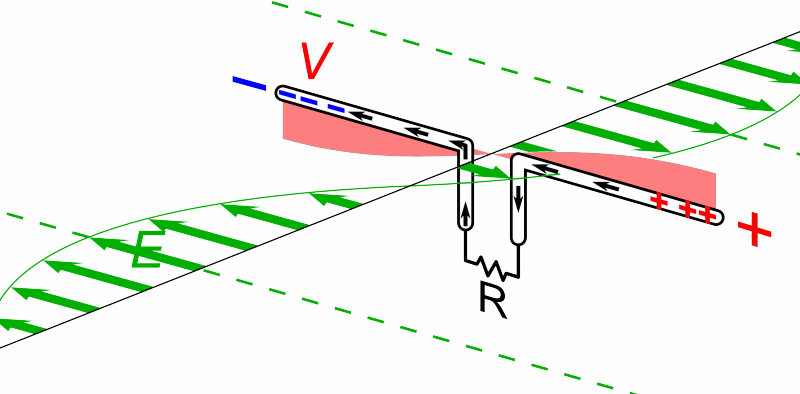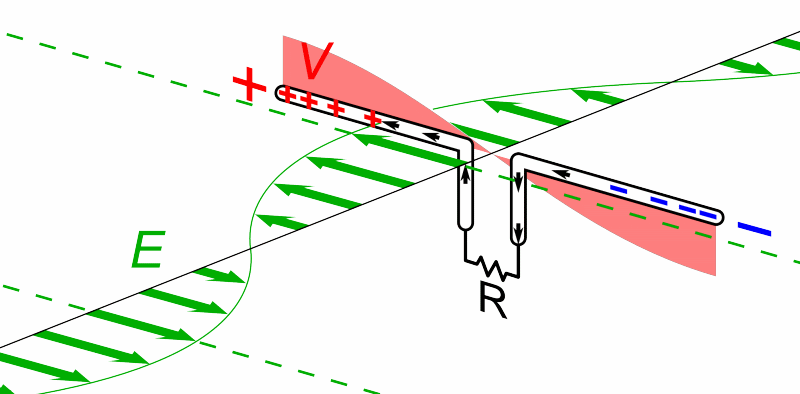
. The dipole is any one of a class of antennas producing a radiation pattern approximating that of an elementary electric dipole with a radiating structure supporting a line current so energized that the current has only one node at each end. A dipole antenna commonly consists of two identical conductive elements such as metal wires or rods. The driving current from the transmitter is applied, or for receiving antennas the output signal to the receiver is taken, between the two halves of the antenna. Each side of the feedline
In a radio antenna, the feed line (feedline), or feeder, is the cable or other transmission line that connects the antenna with the radio transmitter or receiver. In a transmitting antenna, it feeds the radio frequency (RF) current from t ...
to the transmitter or receiver is connected to one of the conductors. This contrasts with a monopole antenna, which consists of a single rod or conductor with one side of the feedline connected to it, and the other side connected to some type of ground. A common example of a dipole is the "rabbit ears" television antenna found on broadcast television sets.
The dipole is the simplest type of antenna from a theoretical point of view. Most commonly it consists of two conductors of equal length oriented end-to-end with the feedline connected between them. Dipoles are frequently used as resonant antennas. If the feedpoint of such an antenna is shorted, then it will be able to resonate at a particular frequency, just like a guitar string that is plucked. Using the antenna at around that frequency is advantageous in terms of feedpoint impedance (and thus standing wave ratio), so its length is determined by the intended wavelength
In physics, the wavelength is the spatial period of a periodic wave—the distance over which the wave's shape repeats.
It is the distance between consecutive corresponding points of the same phase on the wave, such as two adjacent crests, tr ...
(or frequency) of operation. The most commonly used is the center-fed half-wave dipole which is just under a half-wavelength long. The radiation pattern of the half-wave dipole is maximum perpendicular to the conductor, falling to zero in the axial direction, thus implementing an omnidirectional antenna if installed vertically, or (more commonly) a weakly directional antenna if horizontal.
Although they may be used as standalone low-gain antennas, dipoles are also employed as driven elements in more complex antenna designs such as the Yagi antenna and driven arrays. Dipole antennas (or such designs derived from them, including the monopole) are used to feed more elaborate directional antennas such as a horn antenna
A horn antenna or microwave horn is an antenna that consists of a flaring metal waveguide shaped like a horn to direct radio waves in a beam. Horns are widely used as antennas at UHF and microwave frequencies, above 300 MHz. They are ...
, parabolic reflector
A parabolic (or paraboloid or paraboloidal) reflector (or dish or mirror) is a reflective surface used to collect or project energy such as light, sound, or radio waves. Its shape is part of a circular paraboloid, that is, the surface genera ...
, or corner reflector. Engineers analyze vertical (or other monopole) antennas on the basis of dipole antennas of which they are one half.
History
German physicistHeinrich Hertz
Heinrich Rudolf Hertz ( ; ; 22 February 1857 – 1 January 1894) was a German physicist who first conclusively proved the existence of the electromagnetic waves predicted by James Clerk Maxwell's equations of electromagnetism. The uni ...
first demonstrated the existence of radio waves in 1887 using what we now know as a dipole antenna (with capacitative end-loading). On the other hand, Guglielmo Marconi empirically found that he could just ground the transmitter (or one side of a transmission line, if used) dispensing with one half of the antenna, thus realizing the ''vertical'' or monopole antenna. For the low frequencies Marconi employed to achieve long-distance communications, this form was more practical; when radio moved to higher frequencies (especially VHF
Very high frequency (VHF) is the ITU designation for the range of radio frequency electromagnetic waves (radio waves) from 30 to 300 megahertz (MHz), with corresponding wavelengths of ten meters to one meter.
Frequencies immediately below VHF ...
transmissions for FM radio and TV) it was advantageous for these much smaller antennas to be entirely atop a tower thus requiring a dipole antenna or one of its variations.
In the early days of radio, the thus-named Marconi antenna (monopole) and the doublet (dipole) were seen as distinct inventions. Now, however, the "monopole" antenna is understood as a special case of a dipole which has a virtual element "underground".
Dipole variations
Short dipole
A short dipole is a dipole formed by two conductors with a total length substantially less than a half wavelength (). Short dipoles are sometimes used in applications where a full half-wave dipole would be too large. They can be analyzed easily using the results obtainedbelow
Below may refer to:
*Earth
* Ground (disambiguation)
*Soil
*Floor
* Bottom (disambiguation)
*Less than
*Temperatures below freezing
*Hell or underworld
People with the surname
*Ernst von Below (1863–1955), German World War I general
*Fred Below ...
for the Hertzian dipole, a fictitious entity. Being shorter than a resonant antenna (half wavelength long) its feedpoint impedance includes a large capacitive reactance requiring a loading coil or other matching network in order to be practical, especially as a transmitting antenna.
To find the far-field electric and magnetic fields generated by a short dipole we use the result shown below for the Hertzian dipole (an infinitesimal current element) at a distance from the current and at an angle to the direction of the current, as being:
:
where the radiator consists of a current of over a short length and in electronics replaces the customary mathematical symbol for the "square root of −1". is the radian frequency () and is the wavenumber (). 0 is the impedance of free space (), which is the ratio of a free space plane wave's electric to magnetic field strength.
Dipole antennas of various lengths
The fundamental resonance of a thin linear conductor occurs at a frequency whose free-space wavelength is ''twice'' the wire's length; i.e. where the conductor is 1/2 wavelength long. Dipole antennas are frequently used at around that frequency and thus termed ''half-wave dipole'' antennas. This important case is dealt with in the next section. Thin linear conductors of length ''l'' are in fact resonant at any integer multiple of a half-wavelength: : where ''λ'' = ''c''/''f'' is the wavelength and ''n'' is an integer. For a center-fed dipole, however, there is a great dissimilarity between ''n'' being odd or being even. Dipoles which are an ''odd'' number of half-wavelengths in length have reasonably low driving point impedances (which are purely resistive at that resonant frequency). However ones which are an ''even'' number of half-wavelengths in length, that is, an integer number of wavelengths in length, have a ''high'' driving point impedance (albeit purely resistive at that resonant frequency). For instance, a full-wave dipole antenna can be made with two half-wavelength conductors placed end to end for a total length of approximately ''L'' = λ. This results in an additional gain over a half-wave dipole of about 2 dB. Full wave dipoles can be used in short wave broadcasting only by making the effective diameter very large and feeding from a high impedance balanced line. Cage dipoles are often used to get the large diameter. A 5/4-wave dipole antenna has a much lower but not purely resistive feedpoint impedance, which requires a matching network to the impedance of the transmission line. Its gain is about 3 dB greater than a half-wave dipole, the highest gain of any dipole of any similar length. Other reasonable lengths of dipole do not offer advantages and are seldom used. However the overtone resonances of a half-wave dipole antenna at odd multiples of its fundamental frequency are sometimes exploited. For instance, amateur radio antennas designed as half-wave dipoles at 7 MHz can also be used as 3/2-wave dipoles at 21 MHz; likewise VHF television antennas resonant at the low VHF television band (centered around 65 MHz) are also resonant at the high VHF television band (around 195 MHz).Half-wave dipole
 A half-wave dipole antenna consists of two quarter-wavelength conductors placed end to end for a total length of approximately ''L'' = λ/2. The current distribution is that of a
A half-wave dipole antenna consists of two quarter-wavelength conductors placed end to end for a total length of approximately ''L'' = λ/2. The current distribution is that of a standing wave
In physics, a standing wave, also known as a stationary wave, is a wave that oscillates in time but whose peak amplitude profile does not move in space. The peak amplitude of the wave oscillations at any point in space is constant with respect ...
, approximately sinusoidal along the length of the dipole, with a node at each end and an antinode (peak current) at the center (feedpoint):
:
where ''k'' = 2''π''/''λ'' and ''z'' runs from −''L''/2 to ''L''/2.
In the far field, this produces a radiation pattern whose electric field is given by
:
The directional factor cos ''π''/2)cos ''θ''sin ''θ'' is barely different from sin ''θ'' applying to the short dipole, resulting in a very similar radiation pattern as noted above.
A numerical integration of the radiated power over all solid angle, as we did for the short dipole, obtains a value for the total power Ptotal radiated by the dipole with a current having a peak value of ''I''0 as in the form specified above. Dividing ''P''total by 4π''R''2 supplies the flux at a distance ''R'' ''averaged'' over all directions. Dividing the flux in the direction (where it is at its peak) at distance R by that average flux, we find the directive gain to be 1.64. This can also be directly computed using the cosine integral
In mathematics, trigonometric integrals are a family of integrals involving trigonometric functions.
Sine integral
The different sine integral definitions are
\operatorname(x) = \int_0^x\frac\,dt
\operatorname(x) = -\int_x^\infty\frac ...
:
: (2.15 dBi)
(Note that the cosine integral
In mathematics, trigonometric integrals are a family of integrals involving trigonometric functions.
Sine integral
The different sine integral definitions are
\operatorname(x) = \int_0^x\frac\,dt
\operatorname(x) = -\int_x^\infty\frac ...
Cin(''x'') is not the same as the cosine integral Ci(''x''). Both MATLAB
MATLAB (an abbreviation of "MATrix LABoratory") is a proprietary multi-paradigm programming language and numeric computing environment developed by MathWorks. MATLAB allows matrix manipulations, plotting of functions and data, implementat ...
and Mathematica have inbuilt functions which compute Ci(''x''), but not Cin(''x''). See the Wikipedia page on cosine integral
In mathematics, trigonometric integrals are a family of integrals involving trigonometric functions.
Sine integral
The different sine integral definitions are
\operatorname(x) = \int_0^x\frac\,dt
\operatorname(x) = -\int_x^\infty\frac ...
for the relationship between these functions.)
We can now also find the radiation resistance as we did for the short dipole by solving:
:
to obtain:
:
Using the induced EMF method, the real part of the driving point impedance can also be written in terms of the cosine integral, obtaining the same result:
:
If a half-wave dipole is driven at a point other the center, then the feed point resistance will be higher. The radiation resistance is ''usually'' expressed relative to the maximum current present along an antenna element, which for the half-wave dipole (and most other antennas) is also the current at the feedpoint. However, if the dipole is fed at a different point at a distance ''x'' from a current maximum (the center in the case of a half-wave dipole), then the current there is not ''I''0 but only ''I''0 cos(''kx''). In order to supply the same power, the voltage at the feedpoint has to be similarly ''increased'' by the factor 1/cos(''kx''). Consequently, the resistive part of the feedpoint impedance Re(''V''/''I'') is increased by the factor 1/cos2(''kx''):
:
This equation can also be used for dipole antennas of other lengths, provided that ''R''radiation has been computed relative to the current maximum, which is ''not'' generally the same as the feedpoint current for dipoles longer than half-wave. Note that this equation breaks down when feeding an antenna near a current node, where cos(kx) approaches zero. Indeed, the driving point impedance rises greatly, but is nevertheless limited due to quadrature components of the elements' current which is ignored in the above model for the current distribution.
Folded dipole
A folded dipole is a half-wave dipole with an additional parallel wire connecting its two ends. If the additional wire has the same diameter and cross-section as the dipole, two nearly identical radiating currents are generated. The resulting far-field emission pattern is nearly identical to the one for the single-wire dipole described above, but at resonance its feedpoint impedance is four times the radiation resistance of a single-wire dipole. A folded "dipole" is, technically, a folded full-waveloop antenna
A loop antenna is a radio antenna consisting of a loop or coil of wire, tubing, or other electrical conductor, that is usually fed by a balanced source or feeding a balanced load. Within this physical description there are two (possibly three) ...
, where the loop has been bent at opposing ends and squashed into two parallel wires in a flat line. Although the broad bandwidth, high feedpoint impedance, and high efficiency are characteristics more similar to a full loop antenna, the folded dipole's radiation pattern is more like an ordinary dipole. Since the operation of a single halfwave dipole is easier to understand, both full loops and folded dipoles are often described as two halfwave dipoles in parallel, connected at the ends.
The high feedpoint impedance at resonance is because for a fixed amount of power, the total radiating current is equal to twice the current in each wire separately and thus equal to twice the current at the feed point. We equate the average radiated power to the average power delivered at the feedpoint, we may write
:,
where is the lower feedpoint impedance of the resonant halfwave dipole. It follows that
:
The folded dipole is therefore well matched to 300 ohm balanced transmission lines, such as twin-feed ribbon cable. The folded dipole has a wider bandwidth than a single dipole. They can be used for transforming the value of input impedance of the dipole over a broad range of step-up ratios by changing the thicknesses of the wire conductors for the fed- and folded-sides. Instead of altering thickness or spacing, one can add a third parallel wire to increase the antenna impedance to 9 times that of a single-wire dipole, raising the impedance to 658 Ω, making a good match for open wire feed cable, and further broadening the resonant frequency band of the antenna.
Half-wave folded dipoles are often used for FM radio antennas; versions made with twin lead
Twin-lead cable is a two-conductor flat cable used as a balanced transmission line to carry radio frequency (RF) signals. It is constructed of two stranded or solid copper or copper-clad steel wires, held a precise distance apart by a plastic ...
which can be hung on an inside wall often come with FM tuners. The T2FD
The ''Tilted Terminated Folded Dipole'' (T²FD, T2FD, or TTFD) or ''Balanced Termination, Folded Dipole'' (BTFD) - also known as W3HH antenna - is a general-purpose shortwave antenna developed in the late 1940s by the United States Navy. It per ...
antenna is a folded dipole. They are also widely used as driven elements for rooftop Yagi television antennas.
Other variants
There are numerous modifications to the shape of a dipole antenna which are useful in one way or another but result in similar radiation characteristics (low gain). This is not to mention the many directional antennas which include one or more dipole elements in their design as driven elements, many of which are linked to in the information box at the bottom of this page. * The ''bow-tie antenna'' is a dipole with flaring, triangular shaped arms. The shape gives it a much wider bandwidth than an ordinary dipole. It is widely used in UHF television antennas. * The '' cage dipole'' is a similar modification in which the bandwidth is increased by using fat cylindrical dipole elements made of a "cage" of wires (see photo). These are used in a few broadband array antennas in the medium wave and shortwave bands for applications such as over-the-horizon radar and radio telescopes.
* A '' halo antenna'' is a half-wave dipole bent into a circle for a nearly uniform radiation pattern in the plane of the circle. When the halo's circle is horizontal, it produces horizontally polarized radiation in a nearly omnidirectional pattern with little power wasted toward the sky, compared to a straight horizontal dipole. In practice, it is categorized both as a bent dipole and as a loop antenna, depending on author preference.
* A '' turnstile antenna'' comprises two dipoles crossed at a right angle and feed system which introduces a quarter-wave phase difference between the currents along the two. With that geometry, the two dipoles do not interact electrically but their fields add in the far-field producing a net radiation pattern which is rather close to
* The '' cage dipole'' is a similar modification in which the bandwidth is increased by using fat cylindrical dipole elements made of a "cage" of wires (see photo). These are used in a few broadband array antennas in the medium wave and shortwave bands for applications such as over-the-horizon radar and radio telescopes.
* A '' halo antenna'' is a half-wave dipole bent into a circle for a nearly uniform radiation pattern in the plane of the circle. When the halo's circle is horizontal, it produces horizontally polarized radiation in a nearly omnidirectional pattern with little power wasted toward the sky, compared to a straight horizontal dipole. In practice, it is categorized both as a bent dipole and as a loop antenna, depending on author preference.
* A '' turnstile antenna'' comprises two dipoles crossed at a right angle and feed system which introduces a quarter-wave phase difference between the currents along the two. With that geometry, the two dipoles do not interact electrically but their fields add in the far-field producing a net radiation pattern which is rather close to isotropic
Isotropy is uniformity in all orientations; it is derived . Precise definitions depend on the subject area. Exceptions, or inequalities, are frequently indicated by the prefix ' or ', hence '' anisotropy''. ''Anisotropy'' is also used to describ ...
, with horizontal polarization in the plane of the elements and circular or elliptical polarization at other angles. Turnstile antennas can be stacked and fed in phase to realize an omnidirectional broadside array or phased for an end-fire array with circular polarization.
* The ''batwing antenna
A batwing or super turnstile antenna is a type of broadcasting antenna used at VHF and UHF frequencies, named for its distinctive shape which resembles a bat wing or bow tie. Stacked arrays of batwing antennas are used as television broadcast ...
'' is a turnstile antenna with its linear elements widened as in a bow-tie antenna, again for the purpose of widening its resonant frequency and thus usable over a larger bandwidth, without re-tuning. When stacked to form an array the radiation is omnidirectional, horizontally polarized, and with increased gain at low elevations, making it ideal for television broadcasting.
* A V (or "Vee") antenna is a dipole with a bend in the middle so its arms are at an angle instead of co-linear.
* A ''quadrant'' antenna is a 'V' antenna with an unusual overall length of a ''full'' wavelength, with two half-wave horizontal elements meeting at a right angle where it is fed. Quadrant antennas produce mostly horizontal polarization at low to intermediate elevation angles and have nearly omnidirectional radiation patterns. One implementation uses "cage" elements (see above); the thickness of the resulting elements lowers the high driving point impedance of a full-wave dipole to a value that accommodates a reasonable match to open wire lines and increases the bandwidth (in terms of SWR) to a full octave. They are used for HF band transmissions.
* The '' G5RV antenna'' is a dipole antenna fed indirectly, through a carefully chosen length of 300 Ω or 450 Ω twin lead
Twin-lead cable is a two-conductor flat cable used as a balanced transmission line to carry radio frequency (RF) signals. It is constructed of two stranded or solid copper or copper-clad steel wires, held a precise distance apart by a plastic ...
, which acts as an impedance matching network to connect (through a balun) to a standard 50 Ω coaxial transmission line.
* The '' sloper antenna'' is a slanted vertical dipole antenna attached to the top of a single tower. The element can be center-fed or can be end-fed as an unbalanced monopole antenna from a transmission line at the top of the tower, in which case the monopole's "ground" connection can better be viewed as a second element comprising the tower and/or transmission line shield.
* The '' inverted "V" antenna'' is likewise supported using a single tower but is a balanced antenna with two symmetric elements angled toward the ground. It is thus a half-wave dipole with a bend in the middle. Like the sloper, this has the practical advantage of elevating the antenna but requiring only a ''single'' tower.
* The ''AS-2259 antenna'' is an inverted-‘V’ dipole antenna used for local communications via Near Vertical Incidence Skywave (NVIS).
Vertical (monopole) antennas
Dipole characteristics
Impedance of dipoles of various lengths
 The feedpoint impedance of a dipole antenna is sensitive to its electrical length and feedpoint position. Therefore, a dipole will generally only perform optimally over a rather narrow bandwidth, beyond which its impedance will become a poor match for the transmitter or receiver (and transmission line). The real (resistive) and imaginary (reactive) components of that impedance, as a function of electrical length, are shown in the accompanying graph. The detailed calculation of these numbers are described
The feedpoint impedance of a dipole antenna is sensitive to its electrical length and feedpoint position. Therefore, a dipole will generally only perform optimally over a rather narrow bandwidth, beyond which its impedance will become a poor match for the transmitter or receiver (and transmission line). The real (resistive) and imaginary (reactive) components of that impedance, as a function of electrical length, are shown in the accompanying graph. The detailed calculation of these numbers are described below
Below may refer to:
*Earth
* Ground (disambiguation)
*Soil
*Floor
* Bottom (disambiguation)
*Less than
*Temperatures below freezing
*Hell or underworld
People with the surname
*Ernst von Below (1863–1955), German World War I general
*Fred Below ...
. Note that the value of the reactance is highly dependent on the diameter of the conductors; this plot is for conductors with a diameter of 0.001 wavelengths.
Dipoles that are much smaller than one half the wavelength of the signal are called ''short dipoles''. These have a very low radiation resistance (and a high capacitive reactance) making them inefficient antennas. More of a transmitter's current is dissipated as heat due to the finite resistance of the conductors which is greater than the radiation resistance. However they can nevertheless be practical receiving antennas for longer wavelengths.
Dipoles whose length is approximately half the wavelength of the signal are called ''half-wave dipoles'' and are widely used as such or as the basis for derivative antenna designs. These have a radiation resistance which is much greater, closer to the characteristic impedances of available transmission lines, and normally much larger than the resistance of the conductors, so that their efficiency approaches 100%. In general radio engineering, the term ''dipole'', if not further qualified, is taken to mean a center-fed half-wave dipole.
 A true half-wave dipole is one half of the wavelength λ in length, where in free space. Such a dipole has a feedpoint impedance consisting of 73Ω resistance and +43Ω reactance, thus presenting a slightly inductive reactance. To cancel that reactance, and present a pure resistance to the feedline, the element is shortened by the factor ''k'' for a net length '''' of:
:
where ''λ'' is the free-space wavelength, ''c'' is the
A true half-wave dipole is one half of the wavelength λ in length, where in free space. Such a dipole has a feedpoint impedance consisting of 73Ω resistance and +43Ω reactance, thus presenting a slightly inductive reactance. To cancel that reactance, and present a pure resistance to the feedline, the element is shortened by the factor ''k'' for a net length '''' of:
:
where ''λ'' is the free-space wavelength, ''c'' is the speed of light
The speed of light in vacuum, commonly denoted , is a universal physical constant that is important in many areas of physics. The speed of light is exactly equal to ). According to the special theory of relativity, is the upper limit fo ...
in free space, and ''f'' is the frequency. The adjustment factor ''k'' which causes feedpoint reactance to be eliminated, depends on the diameter of the conductor, as is plotted in the accompanying graph. ''k'' ranges from about 0.98 for thin wires (diameter, 0.00001 wavelengths) to about 0.94 for thick conductors (diameter, 0.008 wavelengths). This is because the effect of antenna length on reactance (upper graph) is much greater for thinner conductors, so that a smaller deviation from the exact half wavelength is required in order to cancel the 43 Ω inductive reactance it has when exactly λ/2. For the same reason, antennas with thicker conductors have a wider operating bandwidth over which they attain a practical standing wave ratio which is degraded by any remaining reactance.
 For a typical ''k'' of about 0.95, the above formula for the corrected antenna length can be written, for a length in metres as 143/''f'', or a length in feet as 468/''f'' where ''f'' is the frequency in megahertz.
Dipole antennas of lengths approximately equal to any ''odd'' multiple of λ are also resonant, presenting a small reactance (which can be cancelled by a small length adjustment). However these are rarely used. One size that is more practical though is a dipole with a length of wavelengths. Not being close to wavelengths, this antenna's impedance has a large (negative) reactance and can only be used with an impedance matching network (a so-called
For a typical ''k'' of about 0.95, the above formula for the corrected antenna length can be written, for a length in metres as 143/''f'', or a length in feet as 468/''f'' where ''f'' is the frequency in megahertz.
Dipole antennas of lengths approximately equal to any ''odd'' multiple of λ are also resonant, presenting a small reactance (which can be cancelled by a small length adjustment). However these are rarely used. One size that is more practical though is a dipole with a length of wavelengths. Not being close to wavelengths, this antenna's impedance has a large (negative) reactance and can only be used with an impedance matching network (a so-called antenna tuner
An antenna tuner (and any of the names in the list below) is a device that is inserted between a radio transmitter and its antenna; when placed close by the antenna and properly adjusted (tuned) it optimizes power transfer by matching the im ...
). It is a desirable length because such an antenna has the highest gain for any dipole which isn't a great deal longer.
Radiation pattern and gain
A dipole is omnidirectional in the plane perpendicular to the wire axis, with the radiation falling to zero on the axis (off the ends of the antenna). In a half-wave dipole the radiation is maximum perpendicular to the antenna, declining as to zero on the axis. Its radiation pattern in three dimensions (see figure) would be plotted approximately as a toroid (doughnut shape) symmetric about the conductor. When mounted vertically this results in maximum radiation in horizontal directions. When mounted horizontally, the radiation peaks at right angles (90°) to the conductor, with nulls in the direction of the dipole. Neglecting electrical inefficiency, the antenna gain is equal to the directive gain, which is 1.5 (1.76 dBi) for a short dipole, increasing to 1.64 (2.15 dBi) for a half-wave dipole. For a 5/4 wave dipole the gain further increases to about 5.2 dBi, making this length desirable for that reason even though the antenna is then off-resonance. Longer dipoles than that have radiation patterns that are multi-lobed, with poorer gain (unless they are ''much'' longer) even along the strongest lobe. Other enhancements to the dipole (such as including a corner reflector or an array of dipoles) can be considered when more substantial directivity is desired. Such antenna designs, although based on the half-wave dipole, generally acquire their own names.Feeding a dipole antenna
Ideally, a half-wave dipole should be fed using a balanced transmission line matching its typical 65–70 Ω input impedance.Twin lead
Twin-lead cable is a two-conductor flat cable used as a balanced transmission line to carry radio frequency (RF) signals. It is constructed of two stranded or solid copper or copper-clad steel wires, held a precise distance apart by a plastic ...
with a similar impedance is available but seldom used and does not match the balanced antenna terminals of most radio and television receivers. Much more common is the use of common 300 Ω twin lead in conjunction with a ''folded dipole''. The driving point impedance of a half-wave folded dipole is 4 times that of a simple half-wave dipole, thus closely matching that 300 Ω characteristic impedance. Most FM broadcast band tuners and older analog televisions include balanced 300 Ω antenna input terminals. However twin lead has the drawback that it is electrically disturbed by any other nearby conductor (including earth); when used for transmitting, care must be taken not to place it near other conductors.
Many types of coaxial cable (or "coax") have a characteristic impedance of 75 Ω, which would otherwise be a good match for a half-wave dipole. However coax is a single-ended line whereas a center-fed dipole expects a balanced line (such as twin lead). By symmetry, one can see that the dipole's terminals have an equal but opposite voltage, whereas coax has one conductor grounded. Using coax regardless results in an unbalanced line, in which the currents along the two conductors of the transmission line are no longer equal and opposite. Since you then have a ''net current'' along the transmission line, the transmission line becomes an antenna itself, with unpredictable results (since it depends on the path of the transmission line).Baluns: What They Do And How They Do It (W7EL) http://www.eznec.com/Amateur/Articles/Baluns.pdf This will generally alter the antenna's intended radiation pattern, and change the impedance seen at the transmitter or receiver.
A balun is required to use coaxial cable with a dipole antenna. The balun transfers power between the single-ended coax and the balanced antenna, sometimes with an additional change in impedance. A balun can be implemented as a transformer
A transformer is a passive component that transfers electrical energy from one electrical circuit to another circuit, or multiple circuits. A varying current in any coil of the transformer produces a varying magnetic flux in the transformer' ...
which also allows for an impedance transformation. This is usually wound on a ferrite toroidal core. The toroid core material must be suitable for the frequency of use, and in a transmitting antenna it must be of sufficient size to avoid saturation. Other balun designs are mentioned below.
Current balun
A so-called current balun uses a transformer wound on a toroid or rod of magnetic material such as ferrite. All of the current seen at the input goes into one terminal of the balanced antenna. It forms a balun by choking common-mode current. The material isn't critical for 1:1 because there is no transformer action applied to the desired differential current. A related design involves ''two'' transformers and includes a 1:4 impedance transformation.Coax balun
A coax balun is a cost-effective method of eliminating feeder radiation, but is limited to a narrow set of operating frequencies. One easy way to make a balun is to use a length of coaxial cable equal to half a wavelength. The inner core of the cable is linked at each end to one of the balanced connections for a feeder or dipole. One of these terminals should be connected to the inner core of the coaxial feeder. All three braids should be connected together. This then forms a 4:1 balun, which works correctly at only a narrow band of frequencies.Sleeve balun
AtVHF
Very high frequency (VHF) is the ITU designation for the range of radio frequency electromagnetic waves (radio waves) from 30 to 300 megahertz (MHz), with corresponding wavelengths of ten meters to one meter.
Frequencies immediately below VHF ...
frequencies, a sleeve balun can also be built to remove feeder radiation.
Another narrow-band design is to use a ''λ''/4 length of metal pipe. The coaxial cable is placed inside the pipe; at one end the braid is wired to the pipe while at the other end no connection is made to the pipe. The balanced end of this balun is at the end where no connection is made to the pipe. The ''λ''/4 conductor acts as a transformer, converting the zero impedance at the short to the braid into an infinite impedance at the open end. This infinite impedance at the open end of the pipe prevents current flowing into the outer coax formed by the outside of the inner coax shield and the pipe, forcing the current to remain in the inside coax. This balun design is impractical for low frequencies because of the long length of pipe that will be needed.
Common applications
"Rabbit ears" TV antenna
 One of the most common applications of the dipole antenna is the ''rabbit ears'' or ''bunny ears'' television antenna, found atop broadcast television receivers. It is used to receive the VHF terrestrial television bands, consisting in the US of 54 to 88 MHz ( band I) and 174 to 216 MHz ( band III), with wavelengths of 5.5 to 1.4 m. Since this frequency range is much wider than a single fixed dipole antenna can cover, it is made with several degrees of adjustment. It is constructed of two telescoping rods that can each be extended out to about 1 m length (one quarter wavelength at 75 MHz). With control over the segments' length, angle with respect to vertical, and compass angle, one has much more flexibility in optimizing reception than available with a rooftop antenna even if equipped with an
One of the most common applications of the dipole antenna is the ''rabbit ears'' or ''bunny ears'' television antenna, found atop broadcast television receivers. It is used to receive the VHF terrestrial television bands, consisting in the US of 54 to 88 MHz ( band I) and 174 to 216 MHz ( band III), with wavelengths of 5.5 to 1.4 m. Since this frequency range is much wider than a single fixed dipole antenna can cover, it is made with several degrees of adjustment. It is constructed of two telescoping rods that can each be extended out to about 1 m length (one quarter wavelength at 75 MHz). With control over the segments' length, angle with respect to vertical, and compass angle, one has much more flexibility in optimizing reception than available with a rooftop antenna even if equipped with an antenna rotor
An antenna rotator (or antenna rotor) is a device used to change the orientation, within the horizontal plane, of a directional antenna. Most antenna rotators have two parts, the rotator unit and the controller. The controller is normally place ...
.
FM-broadcast-receiving antennas
In contrast to the wide television frequency bands, the FM broadcast band (88-108 MHz) is narrow enough that a dipole antenna can cover it. For fixed use in homes, hi-fi tuners are typically supplied with simple folded dipoles resonant near the center of that band. The feedpoint impedance of a folded dipole, which is quadruple the impedance of a simple dipole, is a good match for 300Ωtwin lead
Twin-lead cable is a two-conductor flat cable used as a balanced transmission line to carry radio frequency (RF) signals. It is constructed of two stranded or solid copper or copper-clad steel wires, held a precise distance apart by a plastic ...
, so that is usually used for the transmission line to the tuner. A common construction is to make the arms of the folded dipole out of twin lead also, shorted at their ends. This flexible antenna can be conveniently taped or nailed to walls, following the contours of mouldings.
Shortwave antenna
Horizontal wire dipole antennas are popular for use on the HF shortwave bands, both for transmitting and shortwave listening. They are usually constructed of two lengths of wire joined by a strain insulator in the center, which is the feedpoint. The ends can be attached to existing buildings, structures, or trees, taking advantage of their heights. If used for transmitting, it is essential that the ends of the antenna be attached to supports through strain insulators with a sufficiently high flashover voltage, since the antenna's high-voltageantinode
A node is a point along a standing wave where the wave has minimum amplitude. For instance, in a vibrating guitar string, the ends of the string are nodes. By changing the position of the end node through frets, the guitarist changes the effect ...
s occur there. Being a balanced antenna, they are best fed with a balun between the (coax) transmission line and the feedpoint.
These are simple to put up for temporary or field use. But they are also widely used by radio amateurs and short wave listeners in fixed locations due to their simple (and inexpensive) construction, while still realizing a resonant antenna at frequencies where resonant antenna elements need to be of quite some size. They are an attractive solution for these frequencies when significant directionality is not desired, and the cost of several such resonant antennas for different frequency bands, built at home, may still be much less than a single commercially produced antenna.
Dipole towers
Antennas for MF and LF radio stations are usually constructed as mast radiators, in which the verticalmast
Mast, MAST or MASt may refer to:
Engineering
* Mast (sailing), a vertical spar on a sailing ship
* Flagmast, a pole for flying a flag
* Guyed mast, a structure supported by guy-wires
* Mooring mast, a structure for docking an airship
* Radio mas ...
itself forms the antenna. Although mast radiators are most commonly monopoles
Monopole may refer to:
* Magnetic monopole, or Dirac monopole, a hypothetical particle that may be loosely described as a magnet with only one pole
* Monopole (mathematics), a connection over a principal bundle G with a section (the Higgs field) ...
, some are dipoles. The metal structure of the mast is divided at its midpoint into two insulated sections to make a vertical dipole, which is driven at the midpoint.
Dipole arrays
 Many types of array antennas are constructed using multiple dipoles, usually half-wave dipoles. The purpose of using multiple dipoles is to increase the directional
Many types of array antennas are constructed using multiple dipoles, usually half-wave dipoles. The purpose of using multiple dipoles is to increase the directional gain
Gain or GAIN may refer to:
Science and technology
* Gain (electronics), an electronics and signal processing term
* Antenna gain
* Gain (laser), the amplification involved in laser emission
* Gain (projection screens)
* Information gain in de ...
of the antenna over the gain of a single dipole; the radiation of the separate dipoles interferes to enhance power radiated in desired directions. In arrays with multiple dipole driven elements, the feedline
In a radio antenna, the feed line (feedline), or feeder, is the cable or other transmission line that connects the antenna with the radio transmitter or receiver. In a transmitting antenna, it feeds the radio frequency (RF) current from t ...
is split using an electrical network in order to provide power to the elements, with careful attention paid to the relative phase delays due to transmission between the common point and each element.
In order to increase antenna gain in horizontal directions (at the expense of radiation towards the sky or towards the ground) one can stack antennas in the vertical direction in a broadside array where the antennas are fed in phase. Doing so with horizontal dipole antennas retains those dipoles' directionality and null in the direction of their elements. However, if each dipole is vertically oriented, in a so-called collinear antenna array
In telecommunications, a collinear antenna array (sometimes colinear antenna array) is an array of dipole or quarter-wave antennas mounted in such a manner that the corresponding elements of each antenna are parallel and collinear; that is, t ...
(see graphic), that null direction becomes vertical and the array acquires an omnidirectional radiation pattern (in the horizontal plane) as is typically desired. Vertical collinear arrays are used in the VHF and UHF frequency bands at which wavelengths the size of the elements are small enough to practically stack several on a mast. They are a higher-gain alternative to quarter-wave ground plane antennas used in fixed base stations for mobile two-way radios, such as police, fire, and taxi dispatchers.
 On the other hand, for a rotating antenna (or one used only towards a particular direction) one may desire increased gain and directivity in a particular horizontal direction. If the broadside array discussed above (whether collinear or not) is turned horizontal, then the one obtains a greater gain in the horizontal direction perpendicular to the antennas, at the expense of most other directions. Unfortunately that also means that the direction ''opposite'' the desired direction also has a high gain, whereas high gain is usually desired in one single direction. The power which is wasted in the reverse direction, however, can be redirected, for instance by using a large planar reflector, as is accomplished in the reflective array antenna, increasing the gain in the desired direction by another 3 dB
An alternative realization of a uni-directional antenna is the ''end-fire array''. In this case the dipoles are again side by side (but not collinear), but fed in progressing phases, arranged so that their waves add coherently in one direction but cancel in the opposite direction. So now, rather than being perpendicular to the array direction as in a broadside array, the directivity is ''in'' the array direction (i.e. the direction of the line connecting their feedpoints) but with one of the opposite directions suppressed.
On the other hand, for a rotating antenna (or one used only towards a particular direction) one may desire increased gain and directivity in a particular horizontal direction. If the broadside array discussed above (whether collinear or not) is turned horizontal, then the one obtains a greater gain in the horizontal direction perpendicular to the antennas, at the expense of most other directions. Unfortunately that also means that the direction ''opposite'' the desired direction also has a high gain, whereas high gain is usually desired in one single direction. The power which is wasted in the reverse direction, however, can be redirected, for instance by using a large planar reflector, as is accomplished in the reflective array antenna, increasing the gain in the desired direction by another 3 dB
An alternative realization of a uni-directional antenna is the ''end-fire array''. In this case the dipoles are again side by side (but not collinear), but fed in progressing phases, arranged so that their waves add coherently in one direction but cancel in the opposite direction. So now, rather than being perpendicular to the array direction as in a broadside array, the directivity is ''in'' the array direction (i.e. the direction of the line connecting their feedpoints) but with one of the opposite directions suppressed.
Yagi antennas
The above described antennas with multiple driven elements require a complex feed system of signal splitting, phasing, distribution to the elements, and impedance matching. A different sort of end-fire array which is much more often used is based on the use of so-called '' parasitic elements''. In the popular high-gain Yagi antenna, only one of the dipoles is actually connected electrically, but the others receive and reradiate power supplied by the driven element. This time, the phasing is accomplished by careful choice of the lengths as well as positions of the parasitic elements, in order to concentrate gain in one direction and largely cancel radiation in the opposite direction (as well as all other directions). Although the realized gain is less than a driven array with the same number of elements, the simplicity of the electrical connections makes the Yagi more practical for consumer applications.Dipole as a reference standard
Antennagain
Gain or GAIN may refer to:
Science and technology
* Gain (electronics), an electronics and signal processing term
* Antenna gain
* Gain (laser), the amplification involved in laser emission
* Gain (projection screens)
* Information gain in de ...
is frequently measured as decibels relative to a half-wave dipole. One reason is that practical antenna measurements need a reference strength to compare the field strength of an antenna under test at a particular distance to. Of course there is no such thing as an isotropic radiator, but the half-wave dipole is well understood and behaved, and can be constructed to be nearly 100% efficient. It is also a fairer comparison, since the gain obtained by the dipole itself is essentially "free," given that almost no antenna design has a smaller directive gain.
For a gain measured relative to a dipole, one says the antenna has a gain
Gain or GAIN may refer to:
Science and technology
* Gain (electronics), an electronics and signal processing term
* Antenna gain
* Gain (laser), the amplification involved in laser emission
* Gain (projection screens)
* Information gain in de ...
of "''x'' dBd" (see decibel). More often, gains are expressed relative to an isotropic radiator, often for advertising reasons as this makes the gain appear higher. In consideration of the known gain of a half-wave dipole, 0 dBd is defined as 2.15 dBi; all gains in dBi are 2.15 higher than gains in dBd.
Hertzian dipole
 The ''Hertzian dipole'' or ''elementary doublet'' refers to a theoretical construction, rather than a physical antenna design: It is an idealized tiny segment of conductor carrying a RF current with constant amplitude and direction along its entire (short) length; a real antenna can be modeled as the combination of many Hertzian dipoles laid end-to-end.
The Hertzian dipole may be defined as a finite oscillating current (in a specified direction) of over a tiny or infinitesimal length at a specified position. The solution of the fields from a Hertzian dipole can be used as the basis for analytical or numerical calculation of the radiation from more complex antenna geometries (such as practical dipoles) by forming the superposition of fields from a large number of Hertzian dipoles comprising the current pattern of the actual antenna. As a function of position, taking the elementary current elements multiplied by infinitesimal lengths , the resulting field pattern then reduces to an
The ''Hertzian dipole'' or ''elementary doublet'' refers to a theoretical construction, rather than a physical antenna design: It is an idealized tiny segment of conductor carrying a RF current with constant amplitude and direction along its entire (short) length; a real antenna can be modeled as the combination of many Hertzian dipoles laid end-to-end.
The Hertzian dipole may be defined as a finite oscillating current (in a specified direction) of over a tiny or infinitesimal length at a specified position. The solution of the fields from a Hertzian dipole can be used as the basis for analytical or numerical calculation of the radiation from more complex antenna geometries (such as practical dipoles) by forming the superposition of fields from a large number of Hertzian dipoles comprising the current pattern of the actual antenna. As a function of position, taking the elementary current elements multiplied by infinitesimal lengths , the resulting field pattern then reduces to an integral
In mathematics, an integral assigns numbers to functions in a way that describes displacement, area, volume, and other concepts that arise by combining infinitesimal data. The process of finding integrals is called integration. Along with ...
over the path of an antenna conductor (modeled as a thin wire).
For the following derivation we shall take the current to be in the direction centered at the origin where , with the sinusoidal time dependence for all quantities being understood. The simplest approach is to use the calculation of the vector potential using the formula for the retarded potential. Although the value of is not unique, we shall constrain it according to the Lorenz gauge
In electromagnetism, the Lorenz gauge condition or Lorenz gauge, for Ludvig Lorenz, is a partial gauge fixing of the electromagnetic vector potential by requiring \partial_\mu A^\mu = 0. The name is frequently confused with Hendrik Lorentz, who ha ...
, and assuming sinusoidal current at radian frequency the retardation of the field is converted just into a phase factor , where the wavenumber in free space and is the distance between the point being considered to the origin (where we assumed the current source to be), thus . This results in a vector potential at position due to that current element only, which we find is purely in the direction (the direction of the current):
:
where is the permeability of free space
The vacuum magnetic permeability (variously ''vacuum permeability'', ''permeability of free space'', ''permeability of vacuum''), also known as the magnetic constant, is the magnetic permeability in a classical vacuum. It is a physical constan ...
. Then using
:
we can solve for the magnetic field , and from that (dependent on us having chosen the Lorenz gauge) the electric field using
:
In spherical coordinates we find that the magnetic field has only a component in the direction:
:
while the electric field has components both in the and directions:
:
where is the impedance of free space.
This solution includes near field terms which are very strong near the source but which are ''not'' radiated. As seen in the accompanying animation, the and fields very close to the source are almost 90° out of phase, thus contributing very little to the Poynting vector by which radiated flux is computed. The near field solution for an antenna element (from the integral using this formula over the length of that element) is the field that can be used to compute the mutual impedance between it and another nearby element.
For computation of the far field radiation pattern, the above equations are simplified as only the terms remain significant:
:.
Radiation resistance
If one knows the far field radiation pattern due to a given antenna current, then it is possible to compute the radiation resistance directly. For the above fields due to the Hertzian dipole, we can compute the power flux according to the Poynting vector, resulting in a power (as averaged over one cycle) of: : Although not required, it is simplest to do the following exercise at a large where the far field expressions for and apply. Consider a large sphere surrounding the source with a radius . We find the power per unit area crossing the surface of that sphere to be in the direction according to: : Integration of this flux over the complete sphere results in: : where is the free space wavelength corresponding to the radian frequency . By definition, the radiation resistance times the average of the square of the current is the net power radiated due to that current, so equating the above to we find: : This method can be used to compute the radiation resistance for any antenna whose far field radiation pattern has been found in terms of a specific antenna current. If ohmic losses in the conductors are neglected, the radiation resistance (considered relative to the feedpoint) is identical to the resistive (real) component of the feedpoint impedance. Unfortunately this exercise tells us nothing about the reactive (imaginary) component of feedpoint impedance, whose calculation is consideredbelow
Below may refer to:
*Earth
* Ground (disambiguation)
*Soil
*Floor
* Bottom (disambiguation)
*Less than
*Temperatures below freezing
*Hell or underworld
People with the surname
*Ernst von Below (1863–1955), German World War I general
*Fred Below ...
.
Directive gain
Using the above expression for the radiated flux given by the Poynting vector, it is also possible to compute the directive gain of the Hertzian dipole. Dividing the total power computed above by we can find the flux averaged over all directions as :. Dividing the flux radiated in a ''particular'' direction by we obtain the directive gain : : The commonly quoted antenna "gain", meaning the peak value of the gain pattern (radiation pattern), is found to be 1.5 to 1.76 dBi, lower than practically any other antenna configuration.Comparison with the short dipole
The Hertzian dipole is ''similar to'' but differs from the short dipole, discussed above. In both cases the conductor is very short compared to a wavelength, so the standing wave pattern present on a half-wave dipole (for instance) is absent. However, with the Hertzian dipole we specified that the current along that conductor is ''constant'' over its short length. This makes the Hertzian dipole useful for analysis of more complex antenna configurations, where every infinitesimal section of that ''real'' antenna's conductor can be modelled as a Hertzian dipole with the current found to be flowing in that real antenna. However a short conductor fed with a RF voltage will ''not'' have a uniform current even along that short range. Rather, a short dipole in real life has a current equal to the feedpoint current at the feedpoint but falling linearly to zero over the length of that short conductor. By placing a ''capacitive hat'', such as a metallic ball, at the end of the conductor, it is possible for its self capacitance to absorb the current from the conductor and better approximate the constant current assumed for the Hertzian dipole. But again, the Hertzian dipole is meant only as a theoretical construct for antenna analysis. The short dipole, with a feedpoint current of , has an ''average'' current over each conductor of only . The above field equations for the Hertzian dipole of length would then predict the ''actual'' fields for a short dipole using that effective current . This would result in a power measured in the far field of ''one quarter'' that given by the above equation for the Poynting vector if we had assumed an element current of . Consequently, it can be seen that the radiation resistance computed for the short dipole is one quarter of that computed above for the Hertzian dipole. But their radiation patterns (and gains) are identical.Detailed calculation of dipole feedpoint impedance
The impedance seen at the feedpoint of a dipole of various lengths has been plotted above, in terms of the real (resistive) component ''R''dipole and the imaginary ( reactive) component ''jX''dipole of that impedance. For the case of an antenna with perfect conductors (no ohmic loss), ''R''dipole is identical to the radiation resistance, which can more easily be computed from the total power in the far-field radiation pattern for a given applied current as we showed for the short dipole. The calculation of ''X''dipole is more difficult.Induced EMF method
Using the ''induced EMF method'' closed form expressions are obtained for both components of the feedpoint impedance; such results are plotted above. The solution depends on an assumption for the form of the current distribution along the antenna conductors. For wavelength to element diameter ratios greater than about 60, the current distribution along each antenna element of length is very well approximated as having the form of the sine function at points along the antenna , with the current reaching zero at the elements' ends, where as follows: : where is the wavenumber given by and the amplitude is set to match a specified driving point current at In cases where an approximately sinusoidal current distribution can be assumed, this method solves for the driving point impedance in closed form using the cosine and sine integral functions and . For a dipole of total length , the resistive and reactive components of the driving point impedance can be expressed as: : where is the radius of the conductors, is again the wavenumber as defined above, is the impedance of free space: and isEuler's constant
Euler's constant (sometimes also called the Euler–Mascheroni constant) is a mathematical constant usually denoted by the lowercase Greek letter gamma ().
It is defined as the limiting difference between the harmonic series and the natural ...
.
Integral methods
The induced EMF method is dependent on the assumption of a sinusoidal current distribution, delivering an accuracy better than about 10% as long as the wavelength to element diameter ratio is greater than about 60. However, for yet larger conductors numerical solutions are required which solve for the conductor's current distribution (rather than ''assuming'' a sinusoidal pattern). This can be based on approximating solutions for either ''Pocklington's integrodifferential equation'' or the ''Hallén integral equation''. These approaches also have greater generality, not being limited to linear conductors. Numerical solution of either is performed using the ''moment method solution'' which requires expansion of that current into a set of basis functions; one simple (but not the best) choice, for instance, is to break up the conductor into ''N'' segments with a constant current assumed along each. After setting an appropriate weighting function the cost may be minimized through the inversion of a ''N''×''N'' matrix. Determination of each matrix element requires at least one double integration involving the weighting functions, which may become computationally intensive. These are simplified if the weighting functions are simply delta functions, which corresponds to fitting the boundary conditions for the current along the conductor at only ''N'' discrete points. Then the ''N''×''N'' matrix must be inverted, which is also computationally intensive as ''N'' increases. In one simple example, Balanis (2011) performs this computation to find the antenna impedance with different ''N'' using Pocklington's method, and finds that with ''N'' > 60 the solutions approach their limiting values to within a few percent.See also
*AM broadcasting
AM broadcasting is radio broadcasting using amplitude modulation (AM) transmissions. It was the first method developed for making audio radio transmissions, and is still used worldwide, primarily for medium wave (also known as "AM band") trans ...
* Amateur radio
* Balun
* Coaxial antenna
*Dipole field strength in free space Dipole field strength in free space, in telecommunications, is the electric field strength caused by a half wave dipole under ideal conditions. The actual field strength in terrestrial environments is calculated by empirical formulas based on this ...
* Driven element
* Electronic symbol
*FM broadcasting
FM broadcasting is a method of radio broadcasting using frequency modulation (FM). Invented in 1933 by American engineer Edwin Armstrong, wide-band FM is used worldwide to provide high fidelity sound over broadcast radio. FM broadcasting is capab ...
* Isotropic antenna
* Omnidirectional antenna
* Shortwave listening
* T-antenna
*Whip antenna
A whip antenna is an antenna consisting of a straight flexible wire or rod. The bottom end of the whip is connected to the radio receiver or transmitter. A whip antenna is a form of monopole antenna. The antenna is designed to be flexible so ...
Notes
References
Elementary, short, and half-wave dipoles
* * *Electromagnetic Waves and Antennas
Electromagnetic Waves and Antennas, Sophocles J. Orfanidis.
Wire Antenna Resources including off center fed dipole (OCFD), dipole calculators and construction sites
Wayback Machine
*https://web.archive.org/web/20070926195106/http://www.nt.hs-bremen.de/peik/asc/asc_antenna_slides.pdf
* *
Jed Z. Buchwald, MIT and the Dibner Institute for the History of Science and Technology (link inactive February 2, 2007; archive accessed from Wayback, March 13, 2011)
External links
AC6V's Homebrew Antennas Links
- simple yet complete tutorial from eham.net
Dipole articles
- s series of pages about the dipole in its various forms {{Authority control Antennas (radio) Heinrich Hertz Radio frequency antenna types Radio technology Articles containing video clips