Cubic plane curve on:
[Wikipedia]
[Google]
[Amazon]
In mathematics, a cubic plane curve is a
 Trilinear equation:
Barycentric equation:
The
Trilinear equation:
Barycentric equation:
The
K001 at Berhard Gibert's Cubics in the Triangle Plane
 Trilinear equation:
Barycentric equation:
The Thomson cubic is the locus of a point such that is on the line , where is the centroid.
The Thomson cubic passes through the following points: incenter, centroid, circumcenter, orthocenter, symmedian point, other triangle centers, the vertices the excenters, the midpoints of sides and the midpoints of the altitudes of . For each point on the cubic but not on a sideline of the cubic, the isogonal conjugate of is also on the cubic.
For graphs and properties, se
Trilinear equation:
Barycentric equation:
The Thomson cubic is the locus of a point such that is on the line , where is the centroid.
The Thomson cubic passes through the following points: incenter, centroid, circumcenter, orthocenter, symmedian point, other triangle centers, the vertices the excenters, the midpoints of sides and the midpoints of the altitudes of . For each point on the cubic but not on a sideline of the cubic, the isogonal conjugate of is also on the cubic.
For graphs and properties, se
 Trilinear equation:
Barycentric equation:
The Darboux cubic is the locus of a point such that is on the line , where is the
Trilinear equation:
Barycentric equation:
The Darboux cubic is the locus of a point such that is on the line , where is the
K004 at Cubics in the Triangle Plane
K005 at Cubics in the Triangle Plane
 Trilinear equation:
Barycentric equation:
The Lucas cubic is the locus of a point such that the cevian triangle of is the pedal triangle of some point; the point lies on the Darboux cubic.
The Lucas cubic passes through the centroid, orthocenter, Gergonne point, Nagel point, de Longchamps point, other triangle centers, the vertices of the anticomplementary triangle, and the foci of the Steiner circumellipse.
For graphics and properties, se
Trilinear equation:
Barycentric equation:
The Lucas cubic is the locus of a point such that the cevian triangle of is the pedal triangle of some point; the point lies on the Darboux cubic.
The Lucas cubic passes through the centroid, orthocenter, Gergonne point, Nagel point, de Longchamps point, other triangle centers, the vertices of the anticomplementary triangle, and the foci of the Steiner circumellipse.
For graphics and properties, se
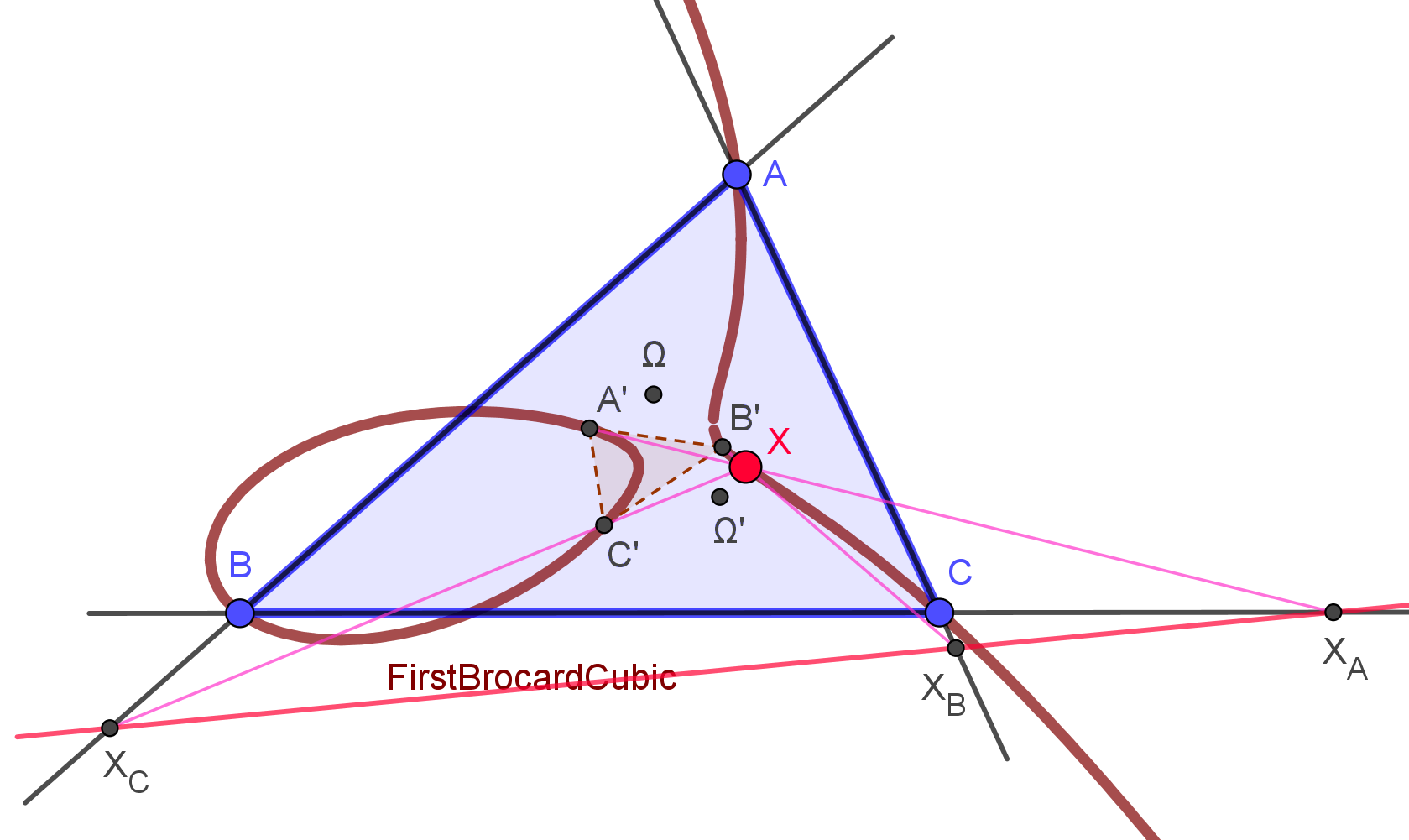 Trilinear equation:
Barycentric equation:
Let be the 1st Brocard triangle. For arbitrary point , let be the intersections of the lines with the sidelines respectively. The 1st Brocard cubic is the locus of for which the points are collinear.
The 1st Brocard cubic passes through the centroid, symmedian point, Steiner point, other triangle centers, and the vertices of the 1st and 3rd Brocard triangles.
For graphics and properties, se
Trilinear equation:
Barycentric equation:
Let be the 1st Brocard triangle. For arbitrary point , let be the intersections of the lines with the sidelines respectively. The 1st Brocard cubic is the locus of for which the points are collinear.
The 1st Brocard cubic passes through the centroid, symmedian point, Steiner point, other triangle centers, and the vertices of the 1st and 3rd Brocard triangles.
For graphics and properties, se
 Trilinear equation:
Barycentric equation:
The 1st equal areas cubic is the locus of a point such that area of the cevian triangle of equals the area of the cevian triangle of . Also, this cubic is the locus of for which is on the line , where is the Steiner point. ( in the
Trilinear equation:
Barycentric equation:
The 1st equal areas cubic is the locus of a point such that area of the cevian triangle of equals the area of the cevian triangle of . Also, this cubic is the locus of for which is on the line , where is the Steiner point. ( in the
K021 at Cubics in the Triangle Plane
K155 at Cubics in the Triangle Plane
A Catalog of Cubic Plane Curves
{{Algebraic curves navbox Algebraic curves
plane algebraic curve
In mathematics, an affine algebraic plane curve is the zero set of a polynomial in two variables. A projective algebraic plane curve is the zero set in a projective plane of a homogeneous polynomial in three variables. An affine algebraic plane c ...
defined by a cubic equation
In algebra, a cubic equation in one variable is an equation of the form
:ax^3+bx^2+cx+d=0
in which is nonzero.
The solutions of this equation are called roots of the cubic function defined by the left-hand side of the equation. If all of th ...
:
applied to homogeneous coordinates
In mathematics, homogeneous coordinates or projective coordinates, introduced by August Ferdinand Möbius in his 1827 work , are a system of coordinates used in projective geometry, just as Cartesian coordinates are used in Euclidean geometry. ...
for the projective plane
In mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect in a single point, but there are some pairs of lines (namely, parallel lines) that d ...
; or the inhomogeneous version for the affine space
In mathematics, an affine space is a geometric structure that generalizes some of the properties of Euclidean spaces in such a way that these are independent of the concepts of distance and measure of angles, keeping only the properties related ...
determined by setting in such an equation. Here is a non-zero linear combination of the third-degree monomial
In mathematics, a monomial is, roughly speaking, a polynomial which has only one term. Two definitions of a monomial may be encountered:
# A monomial, also called power product, is a product of powers of variables with nonnegative integer expone ...
s
:
These are ten in number; therefore the cubic curves form a projective space of dimension 9, over any given field
Field may refer to:
Expanses of open ground
* Field (agriculture), an area of land used for agricultural purposes
* Airfield, an aerodrome that lacks the infrastructure of an airport
* Battlefield
* Lawn, an area of mowed grass
* Meadow, a grass ...
. Each point imposes a single linear condition on , if we ask that pass through . Therefore, we can find some cubic curve through any nine given points, which may be degenerate, and may not be unique, but will be unique and non-degenerate if the points are in general position
In algebraic geometry and computational geometry, general position is a notion of genericity for a set of points, or other geometric objects. It means the ''general case'' situation, as opposed to some more special or coincidental cases that are ...
; compare to two points determining a line and how five points determine a conic
In Euclidean and projective geometry, just as two (distinct) points determine a line (a degree-1 plane curve), five points determine a conic (a degree-2 plane curve). There are additional subtleties for conics that do not exist for lines, and thu ...
. If two cubics pass through a given set of nine points, then in fact a pencil
A pencil () is a writing or drawing implement with a solid pigment core in a protective casing that reduces the risk of core breakage, and keeps it from marking the user's hand.
Pencils create marks by physical abrasion, leaving a trail ...
of cubics does, and the points satisfy additional properties; see Cayley–Bacharach theorem
In mathematics, the Cayley–Bacharach theorem is a statement about cubic curves (plane curves of degree three) in the projective plane . The original form states:
:Assume that two cubics and in the projective plane meet in nine (different) p ...
.
A cubic curve may have a singular point, in which case it has a parametrization in terms of a projective line
In mathematics, a projective line is, roughly speaking, the extension of a usual line by a point called a ''point at infinity''. The statement and the proof of many theorems of geometry are simplified by the resultant elimination of special cases; ...
. Otherwise a ''non-singular'' cubic curve is known to have nine points of inflection
In linguistic morphology, inflection (or inflexion) is a process of word formation in which a word is modified to express different grammatical categories such as tense, case, voice, aspect, person, number, gender, mood, animacy, and ...
, over an algebraically closed
In mathematics, a field is algebraically closed if every non-constant polynomial in (the univariate polynomial ring with coefficients in ) has a root in .
Examples
As an example, the field of real numbers is not algebraically closed, because ...
field such as the complex number
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the fo ...
s. This can be shown by taking the homogeneous version of the Hessian matrix
In mathematics, the Hessian matrix or Hessian is a square matrix of second-order partial derivatives of a scalar-valued function, or scalar field. It describes the local curvature of a function of many variables. The Hessian matrix was developed ...
, which defines again a cubic, and intersecting it with ; the intersections are then counted by Bézout's theorem
Bézout's theorem is a statement in algebraic geometry concerning the number of common zeros of polynomials in indeterminates. In its original form the theorem states that ''in general'' the number of common zeros equals the product of the deg ...
. However, only three of these points may be real, so that the others cannot be seen in the real projective plane by drawing the curve. The nine inflection points of a non-singular cubic have the property that every line passing through two of them contains exactly three inflection points.
The real points of cubic curves were studied by Isaac Newton
Sir Isaac Newton (25 December 1642 – 20 March 1726/27) was an English mathematician, physicist, astronomer, alchemist, theologian, and author (described in his time as a " natural philosopher"), widely recognised as one of the grea ...
. The real points of a non-singular projective cubic fall into one or two 'ovals'. One of these ovals crosses every real projective line, and thus is never bounded when the cubic is drawn in the Euclidean plane; it appears as one or three infinite branches, containing the three real inflection points. The other oval, if it exists, does not contain any real inflection point and appears either as an oval or as two infinite branches. Like for conic section
In mathematics, a conic section, quadratic curve or conic is a curve obtained as the intersection of the surface of a cone with a plane. The three types of conic section are the hyperbola, the parabola, and the ellipse; the circle is a spe ...
s, a line cuts this oval at, at most, two points.
A non-singular plane cubic defines an elliptic curve
In mathematics, an elliptic curve is a smooth, projective, algebraic curve of genus one, on which there is a specified point . An elliptic curve is defined over a field and describes points in , the Cartesian product of with itself. If ...
, over any field for which it has a point defined. Elliptic curves are now normally studied in some variant of Weierstrass's elliptic functions
In mathematics, the Weierstrass elliptic functions are elliptic functions that take a particularly simple form. They are named for Karl Weierstrass. This class of functions are also referred to as ℘-functions and they are usually denoted by t ...
, defining a quadratic extension
In mathematics, particularly in algebra, a field extension is a pair of fields E\subseteq F, such that the operations of ''E'' are those of ''F'' restricted to ''E''. In this case, ''F'' is an extension field of ''E'' and ''E'' is a subfield of ...
of the field of rational functions made by extracting the square root of a cubic. This does depend on having a -rational point
In number theory and algebraic geometry, a rational point of an algebraic variety is a point whose coordinates belong to a given field. If the field is not mentioned, the field of rational numbers is generally understood. If the field is the fiel ...
, which serves as the point at infinity
In geometry, a point at infinity or ideal point is an idealized limiting point at the "end" of each line.
In the case of an affine plane (including the Euclidean plane), there is one ideal point for each pencil of parallel lines of the plane. Ad ...
in Weierstrass form. There are many cubic curves that have no such point, for example when is the rational number
In mathematics, a rational number is a number that can be expressed as the quotient or fraction of two integers, a numerator and a non-zero denominator . For example, is a rational number, as is every integer (e.g. ). The set of all rat ...
field.
The singular points of an irreducible plane cubic curve are quite limited: one double point
In geometry, a singular point on a curve is one where the curve is not given by a smooth embedding of a parameter. The precise definition of a singular point depends on the type of curve being studied.
Algebraic curves in the plane
Algebraic curv ...
, or one cusp
A cusp is the most pointed end of a curve. It often refers to cusp (anatomy), a pointed structure on a tooth.
Cusp or CUSP may also refer to:
Mathematics
* Cusp (singularity), a singular point of a curve
* Cusp catastrophe, a branch of bifurc ...
. A reducible plane cubic curve is either a conic and a line or three lines, and accordingly have two double points or a tacnode
In classical algebraic geometry, a tacnode (also called a point of osculation or double cusp). is a kind of singular point of a curve. It is defined as a point where two (or more) osculating circles to the curve at that point are tangent
I ...
(if a conic and a line), or up to three double points or a single triple point (concurrent lines
In geometry, lines in a plane or higher-dimensional space are said to be concurrent if they intersect at a single point. They are in contrast to parallel lines.
Examples
Triangles
In a triangle, four basic types of sets of concurrent lines ...
) if three lines.
Cubic curves in the plane of a triangle
Suppose that is a triangle with sidelengths Relative to , many named cubics pass through well-known points. Examples shown below use two kinds of homogeneous coordinates: trilinear and barycentric. To convert from trilinear to barycentric in a cubic equation, substitute as follows: : to convert from barycentric to trilinear, use : Many equations for cubics have the form : In the examples below, such equations are written more succinctly in "cyclic sum notation", like this: :. The cubics listed below can be defined in terms of the isogonal conjugate, denoted by , of a point not on a sideline of . A construction of follows. Let be the reflection of line about the internal angle bisector of angle , and define and analogously. Then the three reflected lines concur in . In trilinear coordinates, if thenNeuberg cubic
 Trilinear equation:
Barycentric equation:
The
Trilinear equation:
Barycentric equation:
The Neuberg cubic
In Euclidean geometry, the Neuberg cubic is a special cubic plane curve associated with a reference triangle with several remarkable properties. It is named after Joseph Jean Baptiste Neuberg (30 October 1840 – 22 March 1926), a Luxembourger mat ...
(named after Joseph Jean Baptiste Neuberg
Joseph Jean Baptiste Neuberg (30 October 1840 – 22 March 1926) was a Luxembourger mathematician who worked primarily in geometry.
Biography
Neuberg was born on 30 October 1840 in Luxembourg City, Luxembourg. He first studied at a local scho ...
) is the locus
Locus (plural loci) is Latin for "place". It may refer to:
Entertainment
* Locus (comics), a Marvel Comics mutant villainess, a member of the Mutant Liberation Front
* ''Locus'' (magazine), science fiction and fantasy magazine
** ''Locus Award' ...
of a point such that is on the line , where is the Euler infinity point ( in the Encyclopedia of Triangle Centers
The Encyclopedia of Triangle Centers (ETC) is an online list of thousands of points or " centers" associated with the geometry of a triangle. It is maintained by Clark Kimberling, Professor of Mathematics at the University of Evansville.
, the ...
). Also, this cubic is the locus of such that the triangle is perspective to , where is the reflection of in the lines respectively
The Neuberg cubic passes through the following points: incenter
In geometry, the incenter of a triangle is a triangle center, a point defined for any triangle in a way that is independent of the triangle's placement or scale. The incenter may be equivalently defined as the point where the internal angle bis ...
, circumcenter
In geometry, the circumscribed circle or circumcircle of a polygon is a circle that passes through all the vertices of the polygon. The center of this circle is called the circumcenter and its radius is called the circumradius.
Not every polyg ...
, orthocenter
In geometry, an altitude of a triangle is a line segment through a vertex and perpendicular to (i.e., forming a right angle with) a line containing the base (the side opposite the vertex). This line containing the opposite side is called the '' ...
, both Fermat point
In Euclidean geometry, the Fermat point of a triangle, also called the Torricelli point or Fermat–Torricelli point, is a point such that the sum of the three distances from each of the three vertices of the triangle to the point is the smallest ...
s, both isodynamic point
In Euclidean geometry, the isodynamic points of a triangle are points associated with the triangle, with the properties that an inversion centered at one of these points transforms the given triangle into an equilateral triangle, and that the dis ...
s, the Euler infinity point, other triangle centers, the excenters, the reflections of in the sidelines of , and the vertices of the six equilateral triangles erected on the sides of .
For a graphical representation and extensive list of properties of the Neuberg cubic, seK001 at Berhard Gibert's Cubics in the Triangle Plane
Thomson cubic
Darboux cubic
 Trilinear equation:
Barycentric equation:
The Darboux cubic is the locus of a point such that is on the line , where is the
Trilinear equation:
Barycentric equation:
The Darboux cubic is the locus of a point such that is on the line , where is the de Longchamps point
In geometry, the de Longchamps point of a triangle is a triangle center named after French mathematician Gaston Albert Gohierre de Longchamps. It is the reflection of the orthocenter of the triangle about the circumcenter..
Definition
Let the ...
. Also, this cubic is the locus of such that the pedal triangle of is the cevian triangle of some point (which lies on the Lucas cubic). Also, this cubic is the locus of a point such that the pedal triangle of and the anticevian triangle of are perspective; the perspector lies on the Thomson cubic.
The Darboux cubic passes through the incenter, circumcenter, orthocenter, de Longchamps point, other triangle centers, the vertices the excenters, and the antipodes of on the circumcircle. For each point on the cubic but not on a sideline of the cubic, the isogonal conjugate of is also on the cubic.
For graphics and properties, seK004 at Cubics in the Triangle Plane
Napoleon–Feuerbach cubic
Trilinear equation: Barycentric equation: The Napoleon–Feuerbach cubic is the locus of a point is on the line , where is the nine-point center, ( in theEncyclopedia of Triangle Centers
The Encyclopedia of Triangle Centers (ETC) is an online list of thousands of points or " centers" associated with the geometry of a triangle. It is maintained by Clark Kimberling, Professor of Mathematics at the University of Evansville.
, the ...
).
The Napoleon–Feuerbach cubic passes through the incenter, circumcenter, orthocenter, 1st and 2nd Napoleon points, other triangle centers, the vertices the excenters, the projections of the centroid on the altitudes, and the centers of the 6 equilateral triangles erected on the sides of .
For a graphics and properties, seK005 at Cubics in the Triangle Plane
Lucas cubic
 Trilinear equation:
Barycentric equation:
The Lucas cubic is the locus of a point such that the cevian triangle of is the pedal triangle of some point; the point lies on the Darboux cubic.
The Lucas cubic passes through the centroid, orthocenter, Gergonne point, Nagel point, de Longchamps point, other triangle centers, the vertices of the anticomplementary triangle, and the foci of the Steiner circumellipse.
For graphics and properties, se
Trilinear equation:
Barycentric equation:
The Lucas cubic is the locus of a point such that the cevian triangle of is the pedal triangle of some point; the point lies on the Darboux cubic.
The Lucas cubic passes through the centroid, orthocenter, Gergonne point, Nagel point, de Longchamps point, other triangle centers, the vertices of the anticomplementary triangle, and the foci of the Steiner circumellipse.
For graphics and properties, se1st Brocard cubic
 Trilinear equation:
Barycentric equation:
Let be the 1st Brocard triangle. For arbitrary point , let be the intersections of the lines with the sidelines respectively. The 1st Brocard cubic is the locus of for which the points are collinear.
The 1st Brocard cubic passes through the centroid, symmedian point, Steiner point, other triangle centers, and the vertices of the 1st and 3rd Brocard triangles.
For graphics and properties, se
Trilinear equation:
Barycentric equation:
Let be the 1st Brocard triangle. For arbitrary point , let be the intersections of the lines with the sidelines respectively. The 1st Brocard cubic is the locus of for which the points are collinear.
The 1st Brocard cubic passes through the centroid, symmedian point, Steiner point, other triangle centers, and the vertices of the 1st and 3rd Brocard triangles.
For graphics and properties, se2nd Brocard cubic
Trilinear equation: Barycentric equation: The 2nd Brocard cubic is the locus of a point for which the pole of the line in the circumconic through and lies on the line of the circumcenter and the symmedian point (i.e., the Brocard axis). The cubic passes through the centroid, symmedian point, both Fermat points, both isodynamic points, the Parry point, other triangle centers, and the vertices of the 2nd and 4th Brocard triangles. For a graphics and properties, se1st equal areas cubic
 Trilinear equation:
Barycentric equation:
The 1st equal areas cubic is the locus of a point such that area of the cevian triangle of equals the area of the cevian triangle of . Also, this cubic is the locus of for which is on the line , where is the Steiner point. ( in the
Trilinear equation:
Barycentric equation:
The 1st equal areas cubic is the locus of a point such that area of the cevian triangle of equals the area of the cevian triangle of . Also, this cubic is the locus of for which is on the line , where is the Steiner point. ( in the Encyclopedia of Triangle Centers
The Encyclopedia of Triangle Centers (ETC) is an online list of thousands of points or " centers" associated with the geometry of a triangle. It is maintained by Clark Kimberling, Professor of Mathematics at the University of Evansville.
, the ...
).
The 1st equal areas cubic passes through the incenter, Steiner point, other triangle centers, the 1st and 2nd Brocard points, and the excenters.
For a graphics and properties, seK021 at Cubics in the Triangle Plane
2nd equal areas cubic
Trilinear equation: Barycentric equation: For any point (trilinears), let and The 2nd equal areas cubic is the locus of such that the area of the cevian triangle of equals the area of the cevian triangle of . The 2nd equal areas cubic passes through the incenter, centroid, symmedian point, and points inEncyclopedia of Triangle Centers
The Encyclopedia of Triangle Centers (ETC) is an online list of thousands of points or " centers" associated with the geometry of a triangle. It is maintained by Clark Kimberling, Professor of Mathematics at the University of Evansville.
, the ...
indexed as ''X''(31), ''X''(105), ''X''(238), ''X''(292), ''X''(365), ''X''(672), ''X''(1453), ''X''(1931), ''X''(2053), and others.
For a graphics and properties, seK155 at Cubics in the Triangle Plane
See also
*Cayley–Bacharach theorem
In mathematics, the Cayley–Bacharach theorem is a statement about cubic curves (plane curves of degree three) in the projective plane . The original form states:
:Assume that two cubics and in the projective plane meet in nine (different) p ...
, on the intersection of two cubic plane curves
* Twisted cubic
In mathematics, a twisted cubic is a smooth, rational curve ''C'' of degree three in projective 3-space P3. It is a fundamental example of a skew curve. It is essentially unique, up to projective transformation (''the'' twisted cubic, therefore). ...
, a cubic space curve
* Elliptic curve
In mathematics, an elliptic curve is a smooth, projective, algebraic curve of genus one, on which there is a specified point . An elliptic curve is defined over a field and describes points in , the Cartesian product of with itself. If ...
* Witch of Agnesi
In mathematics, the witch of Agnesi () is a cubic plane curve defined from two diametrically opposite points of a circle. It gets its name from Italian mathematician Maria Gaetana Agnesi, and from a mistranslation of an Italian word for a sail ...
* Catalogue of Triangle Cubics
The Catalogue of Triangle Cubics is an online resource containing detailed information about more than 1200 cubic curves in the plane of a reference triangle. The resource is maintained by Bernard Gilbert. Each cubic in the resource is assigned a ...
References
*. *. *. *. *. *. *. *. *. *. See Chapter 8 for cubics. *. *. *. *.External links
A Catalog of Cubic Plane Curves
{{Algebraic curves navbox Algebraic curves