Computation of radiowave attenuation in the atmosphere on:
[Wikipedia]
[Google]
[Amazon]
The computation of radiowave attenuation in the atmosphere is a series of
for download
and is available to the public.
 The document ITU-R pp. 676–78 of the
The document ITU-R pp. 676–78 of the
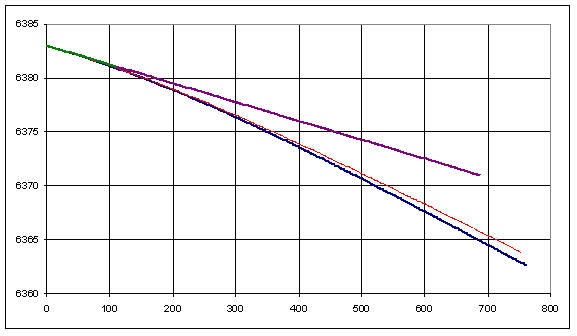 Note that 22.5 GHz is not a practical frequency but it is the most suitable for algorithms comparison. In the table, the first column gives the results in dB, the third gives the distance covered and the last gives the final altitude. Distances are in km. From the altitude 30 km up, the attenuation is negligible. The paths of the three are plotted:
Note: A
Note that 22.5 GHz is not a practical frequency but it is the most suitable for algorithms comparison. In the table, the first column gives the results in dB, the third gives the distance covered and the last gives the final altitude. Distances are in km. From the altitude 30 km up, the attenuation is negligible. The paths of the three are plotted:
Note: A
 Note the way the solution bvp bends over the straight line. A consequence of this property is that the ray can reach locations situated below the horizon of S. This is consistent with observations. The trajectory is a
Note the way the solution bvp bends over the straight line. A consequence of this property is that the ray can reach locations situated below the horizon of S. This is consistent with observations. The trajectory is a
ITU PublicationsJPL Publication 09-14
{{DEFAULTSORT:Radiowave Attenuation in the Atmosphere, Computation Of Applied mathematics Radio technology Atmospheric optical phenomena
radio propagation model
Radio propagation is the behavior of radio waves as they travel, or are propagated, from one point to another in vacuum, or into various parts of the atmosphere.
As a form of electromagnetic radiation, like light waves, radio waves are affected ...
s and methods to estimate the path loss
Path loss, or path attenuation, is the reduction in power density (attenuation) of an electromagnetic wave as it propagates through space. Path loss is a major component in the analysis and design of the link budget of a telecommunication system ...
due to attenuation
In physics, attenuation (in some contexts, extinction) is the gradual loss of flux intensity through a medium. For instance, dark glasses attenuate sunlight, lead attenuates X-rays, and water and air attenuate both light and sound at var ...
of the signal passing through the atmosphere
An atmosphere () is a layer of gas or layers of gases that envelop a planet, and is held in place by the gravity of the planetary body. A planet retains an atmosphere when the gravity is great and the temperature of the atmosphere is low. A ...
by the absorption
Absorption may refer to:
Chemistry and biology
*Absorption (biology), digestion
**Absorption (small intestine)
*Absorption (chemistry), diffusion of particles of gas or liquid into liquid or solid materials
*Absorption (skin), a route by which s ...
of its different components. There are many well-known facts on the phenomenon and qualitative treatments in textbook
A textbook is a book containing a comprehensive compilation of content in a branch of study with the intention of explaining it. Textbooks are produced to meet the needs of educators, usually at educational institutions. Schoolbooks are textbook ...
s.''Antennas and radiowave propagation''. Robert E. Collin. McGraw-Hill College, 1985 A document published by the International Telecommunication Union
The International Telecommunication Union is a specialized agency of the United Nations responsible for many matters related to information and communication technologies. It was established on 17 May 1865 as the International Telegraph Unio ...
(ITU)
''ITU recommendation ITU-R'' pp. 676–78, 2009
provides some basis for a quantitative assessment of the attenuation. That document describes a simplified model along with semi-empirical formulas based on data fitting. It also recommended an algorithm
In mathematics and computer science, an algorithm () is a finite sequence of rigorous instructions, typically used to solve a class of specific problems or to perform a computation. Algorithms are used as specifications for performing ...
to compute the attenuation of radiowave propagation in the atmosphere. NASA
The National Aeronautics and Space Administration (NASA ) is an independent agency of the US federal government responsible for the civil space program, aeronautics research, and space research.
NASA was established in 1958, succeedin ...
also published a study on a related subject.''http://trs-new.jpl.nasa.gov/dspace/handle/2014/41145'' . NASA progress report Free software from CNES
The (CNES; French: ''Centre national d'études spatiales'') is the French government space agency (administratively, a "public administration with industrial and commercial purpose"). Its headquarters are located in central Paris and it is und ...
based on ITU-R
The ITU Radiocommunication Sector (ITU-R) is one of the three sectors (divisions or units) of the International Telecommunication Union (ITU) and is responsible for radio communications.
Its role is to manage the international radio-frequency ...
recommendations is availablfor download
and is available to the public.
The model and the ITU recommendation
 The document ITU-R pp. 676–78 of the
The document ITU-R pp. 676–78 of the ITU-R
The ITU Radiocommunication Sector (ITU-R) is one of the three sectors (divisions or units) of the International Telecommunication Union (ITU) and is responsible for radio communications.
Its role is to manage the international radio-frequency ...
section considers the atmosphere as being divided into spherical homogeneous layers; each layer has a constant refraction index
In optics, the refractive index (or refraction index) of an optical medium is a dimensionless number that gives the indication of the light bending ability of that medium.
The refractive index determines how much the path of light is bent, or ...
. By the use of trigonometry
Trigonometry () is a branch of mathematics that studies relationships between side lengths and angles of triangles. The field emerged in the Hellenistic world during the 3rd century BC from applications of geometry to astronomical studies. ...
, a couple of formulas and an algorithm were derived.
Through the use of an invariant, the same results can be directly derived:
An incident ray
In optics a ray is an idealized geometrical model of light, obtained by choosing a curve that is perpendicular to the ''wavefronts'' of the actual light, and that points in the direction of energy flow. Rays are used to model the propagation o ...
at A under the angle Φ hits the layer B at the angle ''θ''. From basic Euclidean geometry
Euclidean geometry is a mathematical system attributed to ancient Greek mathematician Euclid, which he described in his textbook on geometry: the '' Elements''. Euclid's approach consists in assuming a small set of intuitively appealing axioms ...
:
:
By Snell's law
Snell's law (also known as Snell–Descartes law and ibn-Sahl law and the law of refraction) is a formula used to describe the relationship between the angles of incidence and refraction, when referring to light or other waves passing throug ...
:
:
so that
:
Notes:
* One proof starts from the Fermat's principle
Fermat's principle, also known as the principle of least time, is the link between ray optics and wave optics. In its original "strong" form, Fermat's principle states that the path taken by a ray between two given points is the pat ...
. As a result, one gets proof of the Snell's law along with this invariance. This invariant is valid in a more general situation; the spherical radius is then replaced by the radius of curvature
In differential geometry, the radius of curvature, , is the reciprocal of the curvature. For a curve, it equals the radius of the circular arc which best approximates the curve at that point. For surfaces, the radius of curvature is the radius o ...
at points along the ray. It is also used in equation (4) of the 2005 NASA's report in an application of satellite tracking.
* The assumption of the refraction index varying with the latitude is not strictly compatible with the notion of layers. However the variation of the index is very small, this point is usually ignored in practice.
The ITU recommended algorithm consists of launching a ray from a radio source, then at each step, a layer is chosen and a new incidence angle is then computed. The process is iterated until the altitude of the target is reached. At each step, the covered distance ''dL'' is multiplied by a specific attenuation coefficient
In mathematics, a coefficient is a multiplicative factor in some term of a polynomial, a series, or an expression; it is usually a number, but may be any expression (including variables such as , and ). When the coefficients are themselves var ...
''g'' expressed in dB/km. All the increments ''g'' ''dL'' are added to provide the total attenuation.
Note that the algorithm does not guaranty that the target is actually reached. For this, a much harder boundary value problem
In mathematics, in the field of differential equations, a boundary value problem is a differential equation together with a set of additional constraints, called the boundary conditions. A solution to a boundary value problem is a solution to t ...
would have to be solved.
The eikonal equation
This equation is discussed in the references.''Methods in Electromagnetic Wave Propagation''. D. S. Jones, Oxford, 1987 The equation is highly non-linear. Given that a smooth data fitting curve n(altitude) is provided by the ITU for the refraction index n, and that the values of n differs from 1 only by something of the order 10−4, anumerical solution
Numerical analysis is the study of algorithms that use numerical approximation (as opposed to symbolic manipulations) for the problems of mathematical analysis (as distinguished from discrete mathematics). It is the study of numerical methods th ...
of the eikonal equation
An eikonal equation (from Greek εἰκών, image) is a non-linear first-order partial differential equation that is encountered in problems of wave propagation.
The classical eikonal equation in geometric optics is a differential equation of ...
can be considered. Usually the equation is presented under the self-adjoint form, a more tractable equation for the ray head position vector r is given in generic parametric form:
:
Implementations
Three implementations to compute the attenuations exist: * Take the ray to be a straight line. * Use the optical invariant and apply the ITU recommendation. * Solve the eikonal equation. The first two are only of 1st order approximation (seeOrders of approximation
In science, engineering, and other quantitative disciplines, order of approximation refers to formal or informal expressions for how accurate an approximation is.
Usage in science and engineering
In formal expressions, the ordinal number used b ...
). For the eikonal equation
An eikonal equation (from Greek εἰκών, image) is a non-linear first-order partial differential equation that is encountered in problems of wave propagation.
The classical eikonal equation in geometric optics is a differential equation of ...
, many numerical schemes are available. Here only a simple second order scheme was chosen. For most standard configurations of source-target, the three methods differ little from each other. It is only in the case of rays grazing the ground that the differences are meaningful. The following was used for testing:
At the latitude of 10°, when a ray starts at 5 km altitude with an elevation angle of −1° to hit a target at the same longitude but at latitude 8.84° and altitude 30 km. At 22.5 GHz, the results are:
 Note that 22.5 GHz is not a practical frequency but it is the most suitable for algorithms comparison. In the table, the first column gives the results in dB, the third gives the distance covered and the last gives the final altitude. Distances are in km. From the altitude 30 km up, the attenuation is negligible. The paths of the three are plotted:
Note: A
Note that 22.5 GHz is not a practical frequency but it is the most suitable for algorithms comparison. In the table, the first column gives the results in dB, the third gives the distance covered and the last gives the final altitude. Distances are in km. From the altitude 30 km up, the attenuation is negligible. The paths of the three are plotted:
Note: A MATLAB
MATLAB (an abbreviation of "MATrix LABoratory") is a proprietary multi-paradigm programming language and numeric computing environment developed by MathWorks. MATLAB allows matrix manipulations, plotting of functions and data, implementation ...
version for the uplink (Telecommunications link
In a telecommunications network, a link is a communication channel that connects two or more devices for the purpose of data transmission. The link may be a dedicated physical link or a virtual circuit that uses one or more physical links or shar ...
) is available from the ITU
The boundary value problem
When a point S communicates with a point T, the orientation of the ray is specified by an elevation angle. In a naïve way, the angle can be given by tracing a straight line from S to T. This specification does not guarantee that the ray will reach T: the variation of refraction index bends the ray trajectory. The elevation angle has to be modified to take into account the bending effect. For the eikonal equation, this correction can be done by solving aboundary value problem
In mathematics, in the field of differential equations, a boundary value problem is a differential equation together with a set of additional constraints, called the boundary conditions. A solution to a boundary value problem is a solution to t ...
. As the equation is of second order, the problem is well defined. In spite of the lack of a firm theoretical basis for the ITU method, a trial-error by dichotomy (or binary search
In computer science, binary search, also known as half-interval search, logarithmic search, or binary chop, is a search algorithm that finds the position of a target value within a sorted array. Binary search compares the target value to the m ...
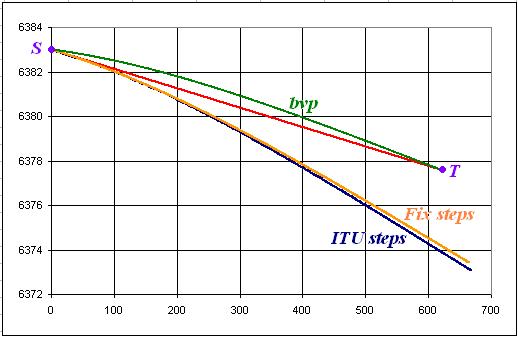
) can also be used. The next figure shows the results of numerical simulations.
The curve labeled as bvp is the trajectory found by correcting the elevation angle. The other two are from a fixed step and a variable step (chosen in accordance with the ITU recommendations) solutions without the elevation angle correction. The nominal elevation angle for this case is −0.5-degree. The numerical results obtained at 22.5 GHz were:
Concave function
In mathematics, a concave function is the negative of a convex function. A concave function is also synonymously called concave downwards, concave down, convex upwards, convex cap, or upper convex.
Definition
A real-valued function f on an in ...
is a consequence of the fact that the gradient of the refraction index is negative, so the Eikonal equation implies that the second derivative of the trajectory is negative. From the point where the ray is parallel to ground, relative to the chosen coordinates, the ray goes down but relative to ground level, the ray goes up.
Often engineers are interested in finding the limits of a system. In this case, a simple idea is to try some low elevation angle and let the ray reach the desired altitude. This point of view has a problem: if suffice to take the angle for which the ray has a tangent point of lowest altitude. For instance with the case of a source at 5 km altitude, of nominal elevation angle −0.5-degree and the target is at 30 km altitude; the attenuation found by the boundary value method is 11.33 dB. The previous point of view of worst case leads to an elevation angle of −1.87-degree and an attenuation of 170.77 dB. With this kind of attenuation, every system would be unusable! It was found also for this case that with the nominal elevation angle, the distance of the tangent point to ground is 5.84 km; that of the worst case is 2.69 km. The nominal distance from source to target is 6383.84 km; for the worst case, it is 990.36 km.
There are many numerical methods to solve boundary value problems.''Initial Value Methods for Boundary Value Problems''. Mayer. Academic Press, 1973 For the Eikonal equation, due to the good behavior of the refraction index just a simple Shooting method
In numerical analysis, the shooting method is a method for solving a boundary value problem by reducing it to an initial value problem. It involves finding solutions to the initial value problem for different initial conditions until one finds the ...
can be used.
See also
* Air mass (astronomy)#Calculation *Ray tracing (physics)
In physics, ray tracing is a method for calculating the path of waves or particles through a system with regions of varying propagation velocity, absorption characteristics, and reflecting surfaces. Under these circumstances, wavefronts may bend, ...
*Radio propagation model
Radio propagation is the behavior of radio waves as they travel, or are propagated, from one point to another in vacuum, or into various parts of the atmosphere.
As a form of electromagnetic radiation, like light waves, radio waves are affected ...
*Path loss
Path loss, or path attenuation, is the reduction in power density (attenuation) of an electromagnetic wave as it propagates through space. Path loss is a major component in the analysis and design of the link budget of a telecommunication system. ...
References
External links
ITU Publications
{{DEFAULTSORT:Radiowave Attenuation in the Atmosphere, Computation Of Applied mathematics Radio technology Atmospheric optical phenomena