Compass-and-straightedge construction on:
[Wikipedia]
[Google]
[Amazon]
 In
In

 The "straightedge" and "compass" of straightedge-and-compass constructions are idealized versions of real-world rulers and compasses.
*The straightedge is an infinitely long edge with no markings on it. It can only be used to draw a line segment between two points, or to extend an existing line segment.
*The compass can have an arbitrarily large radius with no markings on it (unlike certain real-world compasses). Circles and circular arcs can be drawn starting from two given points: the centre and a point on the circle. The compass may or may not collapse (i.e. fold after being taken off the page, erasing its 'stored' radius).
*Lines and circles constructed have infinite precision and zero width.
Actual compasses do not collapse and modern geometric constructions often use this feature. A 'collapsing compass' would appear to be a less powerful instrument. However, by the compass equivalence theorem in Proposition 2 of Book 1 of
The "straightedge" and "compass" of straightedge-and-compass constructions are idealized versions of real-world rulers and compasses.
*The straightedge is an infinitely long edge with no markings on it. It can only be used to draw a line segment between two points, or to extend an existing line segment.
*The compass can have an arbitrarily large radius with no markings on it (unlike certain real-world compasses). Circles and circular arcs can be drawn starting from two given points: the centre and a point on the circle. The compass may or may not collapse (i.e. fold after being taken off the page, erasing its 'stored' radius).
*Lines and circles constructed have infinite precision and zero width.
Actual compasses do not collapse and modern geometric constructions often use this feature. A 'collapsing compass' would appear to be a less powerful instrument. However, by the compass equivalence theorem in Proposition 2 of Book 1 of
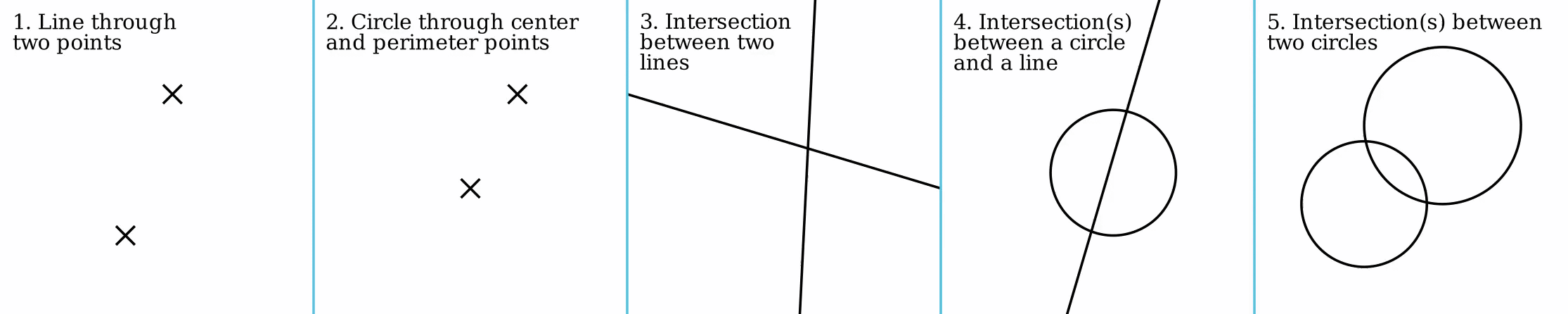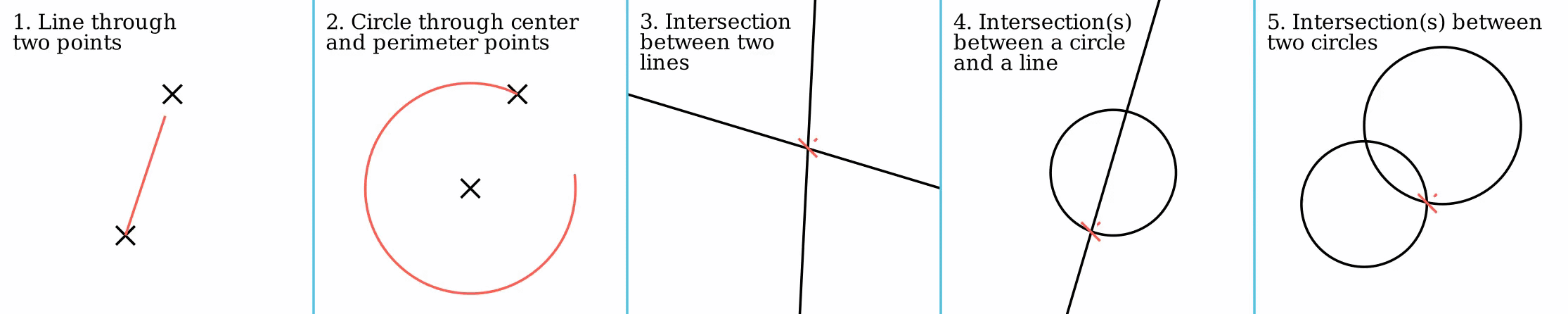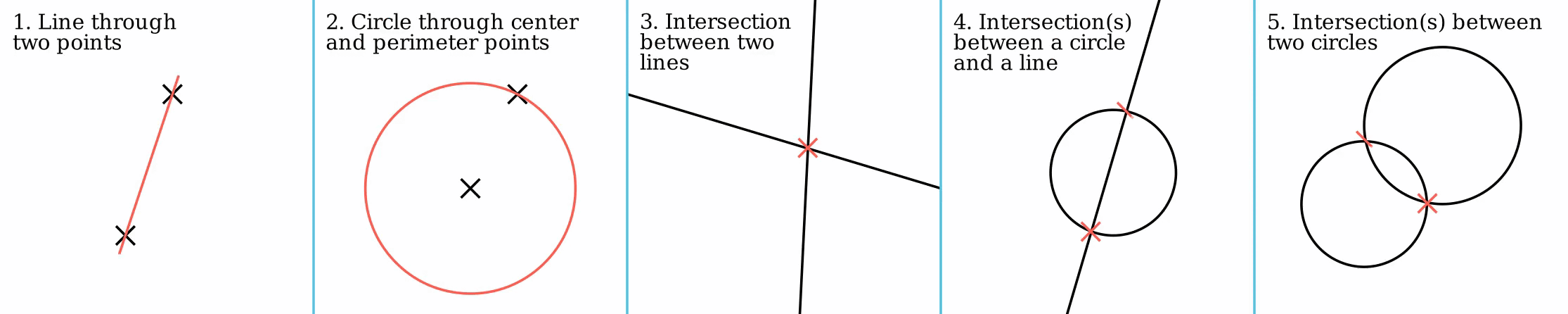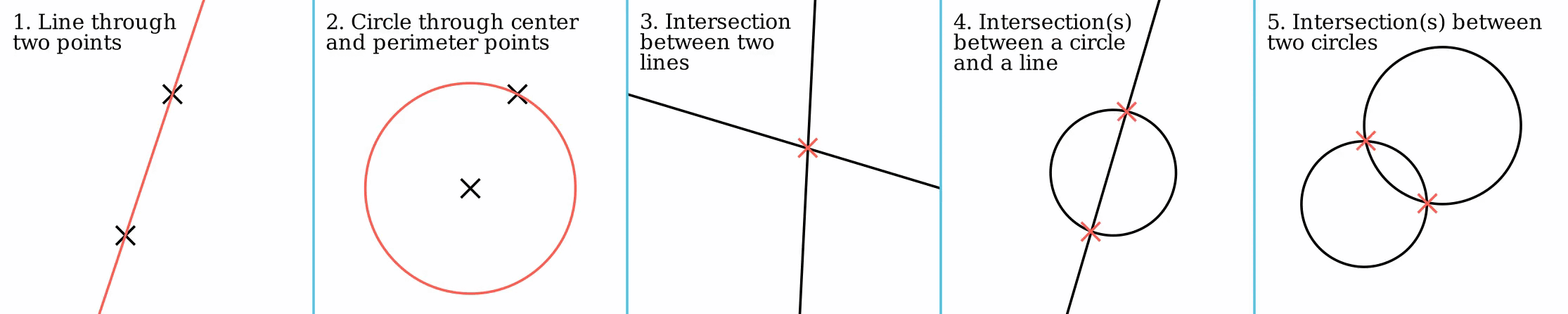 All straightedge-and-compass constructions consist of repeated application of five basic constructions using the points, lines and circles that have already been constructed. These are:
*Creating the
All straightedge-and-compass constructions consist of repeated application of five basic constructions using the points, lines and circles that have already been constructed. These are:
*Creating the
 Some regular polygons (e.g. a
Some regular polygons (e.g. a
Archimedes' trisection
or extract an arbitrary cube root (due to Nicomedes). Hence, any distance whose ratio to an existing distance is the solution of a cubic or a quartic equation is constructible. Using a markable ruler, regular polygons with solid constructions, like the heptagon, are constructible; and
 Given a straight line segment called AB, could this be divided in three new equal segments and in many parts required by the use of intercept theorem
Given a straight line segment called AB, could this be divided in three new equal segments and in many parts required by the use of intercept theorem
Regular polygon constructions
by Dr. Math at ''The Math Forum @ Drexel''
Construction with the Compass Only
at ''cut-the-knot''
Angle Trisection by Hippocrates
at ''cut-the-knot'' * {{Authority control Compass and straightedge constructions,
 In
In geometry
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is c ...
, straightedge-and-compass construction – also known as ruler-and-compass construction, Euclidean construction, or classical construction – is the construction of lengths, angle
In Euclidean geometry, an angle is the figure formed by two rays, called the '' sides'' of the angle, sharing a common endpoint, called the ''vertex'' of the angle.
Angles formed by two rays lie in the plane that contains the rays. Angles ...
s, and other geometric figures using only an idealized ruler and a pair of compass
A compass is a device that shows the cardinal directions used for navigation and geographic orientation. It commonly consists of a magnetized needle or other element, such as a compass card or compass rose, which can pivot to align itself with ...
es.
The idealized ruler, known as a straightedge
A straightedge or straight edge is a tool used for drawing straight lines, or checking their straightness. If it has equally spaced markings along its length, it is usually called a ruler.
Straightedges are used in the automotive service and m ...
, is assumed to be infinite in length, have only one edge, and no markings on it. The compass is assumed to have no maximum or minimum radius, and is assumed to "collapse" when lifted from the page, so may not be directly used to transfer distances. (This is an unimportant restriction since, using a multi-step procedure, a distance can be transferred even with a collapsing compass; see compass equivalence theorem. Note however that whilst a non-collapsing compass held against a straightedge might seem to be equivalent to marking it, the neusis construction is still impermissible and this is what unmarked really means: see Markable rulers below.) More formally, the only permissible constructions are those granted by the first three postulates of Euclid's ''Elements''.
It turns out to be the case that every point constructible using straightedge and compass may also be constructed using compass alone, or by straightedge alone if given a single circle and its center.
The ancient Greek mathematicians first conceived straightedge-and-compass constructions, and a number of ancient problems in plane geometry impose this restriction. The ancient Greeks developed many constructions, but in some cases were unable to do so. Gauss showed that some polygon
In geometry, a polygon () is a plane figure that is described by a finite number of straight line segments connected to form a closed '' polygonal chain'' (or ''polygonal circuit''). The bounded plane region, the bounding circuit, or the two ...
s are constructible but that most are not. Some of the most famous straightedge-and-compass problems were proved impossible by Pierre Wantzel in 1837 using field theory, namely trisecting an arbitrary angle and doubling the volume of a cube (see § impossible constructions). Many of these problems are easily solvable provided that other geometric transformations are allowed; for example, neusis construction can be used to solve the former two problems.
In terms of algebra
Algebra () is one of the broad areas of mathematics. Roughly speaking, algebra is the study of mathematical symbols and the rules for manipulating these symbols in formulas; it is a unifying thread of almost all of mathematics.
Elementary ...
, a length is constructible if and only if
In logic and related fields such as mathematics and philosophy, "if and only if" (shortened as "iff") is a biconditional logical connective between statements, where either both statements are true or both are false.
The connective is bic ...
it represents a constructible number, and an angle is constructible if and only if its cosine is a constructible number. A number is constructible if and only if it can be written using the four basic arithmetic operations and the extraction of square root
In mathematics, a square root of a number is a number such that ; in other words, a number whose '' square'' (the result of multiplying the number by itself, or ⋅ ) is . For example, 4 and −4 are square roots of 16, because .
...
s but of no higher-order roots.
Straightedge and compass tools

 The "straightedge" and "compass" of straightedge-and-compass constructions are idealized versions of real-world rulers and compasses.
*The straightedge is an infinitely long edge with no markings on it. It can only be used to draw a line segment between two points, or to extend an existing line segment.
*The compass can have an arbitrarily large radius with no markings on it (unlike certain real-world compasses). Circles and circular arcs can be drawn starting from two given points: the centre and a point on the circle. The compass may or may not collapse (i.e. fold after being taken off the page, erasing its 'stored' radius).
*Lines and circles constructed have infinite precision and zero width.
Actual compasses do not collapse and modern geometric constructions often use this feature. A 'collapsing compass' would appear to be a less powerful instrument. However, by the compass equivalence theorem in Proposition 2 of Book 1 of
The "straightedge" and "compass" of straightedge-and-compass constructions are idealized versions of real-world rulers and compasses.
*The straightedge is an infinitely long edge with no markings on it. It can only be used to draw a line segment between two points, or to extend an existing line segment.
*The compass can have an arbitrarily large radius with no markings on it (unlike certain real-world compasses). Circles and circular arcs can be drawn starting from two given points: the centre and a point on the circle. The compass may or may not collapse (i.e. fold after being taken off the page, erasing its 'stored' radius).
*Lines and circles constructed have infinite precision and zero width.
Actual compasses do not collapse and modern geometric constructions often use this feature. A 'collapsing compass' would appear to be a less powerful instrument. However, by the compass equivalence theorem in Proposition 2 of Book 1 of Euclid's Elements
The ''Elements'' ( grc, Στοιχεῖα ''Stoikheîa'') is a mathematical treatise consisting of 13 books attributed to the ancient Greek mathematician Euclid in Alexandria, Ptolemaic Egypt 300 BC. It is a collection of definitions, postu ...
, no power is lost by using a collapsing compass. Although the proposition is correct, its proofs have a long and checkered history. In any case, the equivalence is why this feature is not stipulated in the definition of the ideal compass.
Each construction must be mathematically ''exact''. "Eyeballing" distances (looking at the construction and guessing at its accuracy) or using markings on a ruler, are not permitted. Each construction must also ''terminate''. That is, it must have a finite number of steps, and not be the limit of ever closer approximations. (If an unlimited number of steps is permitted, some otherwise-impossible constructions become possible by means of infinite sequences converging to a limit
Limit or Limits may refer to:
Arts and media
* ''Limit'' (manga), a manga by Keiko Suenobu
* ''Limit'' (film), a South Korean film
* Limit (music), a way to characterize harmony
* "Limit" (song), a 2016 single by Luna Sea
* "Limits", a 2019 ...
.)
Stated this way, straightedge-and-compass constructions appear to be a parlour game, rather than a serious practical problem; but the purpose of the restriction is to ensure that constructions can be ''proved'' to be ''exactly'' correct.
History
The ancient Greek mathematicians first attempted straightedge-and-compass constructions, and they discovered how to construct sums, differences, products,ratio
In mathematics, a ratio shows how many times one number contains another. For example, if there are eight oranges and six lemons in a bowl of fruit, then the ratio of oranges to lemons is eight to six (that is, 8:6, which is equivalent to the ...
s, and square root
In mathematics, a square root of a number is a number such that ; in other words, a number whose '' square'' (the result of multiplying the number by itself, or ⋅ ) is . For example, 4 and −4 are square roots of 16, because .
...
s of given lengths. They could also construct half of a given angle, a square whose area is twice that of another square, a square having the same area as a given polygon, and a regular polygon with 3, 4, or 5 sides (or one with twice the number of sides of a given polygon). But they could not construct one third of a given angle except in particular cases, or a square with the same area as a given circle, or a regular polygon with other numbers of sides.Bold, Benjamin. ''Famous Problems of Geometry and How to Solve Them'', Dover Publications, 1982 (orig. 1969). Nor could they construct the side of a cube whose volume would be twice the volume of a cube with a given side.
Hippocrates
Hippocrates of Kos (; grc-gre, Ἱπποκράτης ὁ Κῷος, Hippokrátēs ho Kôios; ), also known as Hippocrates II, was a Greek physician of the classical period who is considered one of the most outstanding figures in the history o ...
and Menaechmus :''There is also a Menaechmus in Plautus' play, ''The Menaechmi''.''
Menaechmus ( el, Μέναιχμος, 380–320 BC) was an ancient Greek mathematician, geometer and philosopher born in Alopeconnesus or Prokonnesos in the Thracian Chersones ...
showed that the volume of the cube could be doubled by finding the intersections of hyperbola
In mathematics, a hyperbola (; pl. hyperbolas or hyperbolae ; adj. hyperbolic ) is a type of smooth curve lying in a plane, defined by its geometric properties or by equations for which it is the solution set. A hyperbola has two pieces, ca ...
s and parabola
In mathematics, a parabola is a plane curve which is mirror-symmetrical and is approximately U-shaped. It fits several superficially different mathematical descriptions, which can all be proved to define exactly the same curves.
One descri ...
s, but these cannot be constructed by straightedge and compass. In the fifth century BCE, Hippias used a curve that he called a quadratrix
In geometry, a quadratrix () is a curve having ordinates which are a measure of the area (or quadrature) of another curve. The two most famous curves of this class are those of Dinostratus and E. W. Tschirnhaus, which are both related to the circ ...
to both trisect the general angle and square the circle, and Nicomedes Nicomedes may refer to:
*Nicomedes (mathematician), ancient Greek mathematician who discovered the conchoid
*Nicomedes of Sparta, regent during the youth of King Pleistoanax, commanded the Spartan army at the Battle of Tanagra (457 BC)
*Saint Nicom ...
in the second century BCE showed how to use a conchoid to trisect an arbitrary angle; but these methods also cannot be followed with just straightedge and compass.
No progress on the unsolved problems was made for two millennia, until in 1796 Gauss showed that a regular polygon with 17 sides could be constructed; five years later he showed the sufficient criterion for a regular polygon of ''n'' sides to be constructible.
In 1837 Pierre Wantzel published a proof of the impossibility of trisecting an arbitrary angle or of doubling the volume of a cube, based on the impossibility of constructing cube roots of lengths. He also showed that Gauss's sufficient constructibility condition for regular polygons is also necessary.
Then in 1882 Lindemann Lindemann is a German surname.
Persons
Notable people with the surname include:
Arts and entertainment
* Elisabeth Lindemann, German textile designer and weaver
*Jens Lindemann, trumpet player
* Julie Lindemann, American photographer
* Maggie ...
showed that is a transcendental number
In mathematics, a transcendental number is a number that is not algebraic—that is, not the root of a non-zero polynomial of finite degree with rational coefficients. The best known transcendental numbers are and .
Though only a few classes ...
, and thus that it is impossible by straightedge and compass to construct a square with the same area as a given circle.
The basic constructions
 All straightedge-and-compass constructions consist of repeated application of five basic constructions using the points, lines and circles that have already been constructed. These are:
*Creating the
All straightedge-and-compass constructions consist of repeated application of five basic constructions using the points, lines and circles that have already been constructed. These are:
*Creating the line
Line most often refers to:
* Line (geometry), object with zero thickness and curvature that stretches to infinity
* Telephone line, a single-user circuit on a telephone communication system
Line, lines, The Line, or LINE may also refer to:
Art ...
through two points
*Creating the circle
A circle is a shape consisting of all points in a plane that are at a given distance from a given point, the centre. Equivalently, it is the curve traced out by a point that moves in a plane so that its distance from a given point is cons ...
that contains one point and has a center at another point
*Creating the point at the intersection of two (non-parallel) lines
*Creating the one point or two points in the intersection of a line and a circle (if they intersect)
*Creating the one point or two points in the intersection of two circles (if they intersect).
For example, starting with just two distinct points, we can create a line or either of two circles (in turn, using each point as centre and passing through the other point). If we draw both circles, two new points are created at their intersections. Drawing lines between the two original points and one of these new points completes the construction of an equilateral triangle.
Therefore, in any geometric problem we have an initial set of symbols (points and lines), an algorithm, and some results. From this perspective, geometry is equivalent to an axiomatic algebra
Algebra () is one of the broad areas of mathematics. Roughly speaking, algebra is the study of mathematical symbols and the rules for manipulating these symbols in formulas; it is a unifying thread of almost all of mathematics.
Elementary ...
, replacing its elements by symbols. Probably Gauss first realized this, and used it to prove the impossibility of some constructions; only much later did Hilbert find a complete set of axioms for geometry.
Common straightedge-and-compass constructions
The most-used straightedge-and-compass constructions include: * Constructing the perpendicular bisector from a segment * Finding the midpoint of a segment. * Drawing a perpendicular line from a point to a line. * Bisecting an angle * Mirroring a point in a line * Constructing a line through a point tangent to a circle * Constructing a circle through 3 noncollinear points * Drawing a line through a given point parallel to a given line.Constructible points
One can associate an algebra to our geometry using aCartesian coordinate system
A Cartesian coordinate system (, ) in a plane is a coordinate system that specifies each point uniquely by a pair of numerical coordinates, which are the signed distances to the point from two fixed perpendicular oriented lines, measured in ...
made of two lines, and represent points of our plane by vectors. Finally we can write these vectors as complex numbers.
Using the equations for lines and circles, one can show that the points at which they intersect lie in a quadratic extension
In mathematics, particularly in algebra, a field extension is a pair of fields E\subseteq F, such that the operations of ''E'' are those of ''F'' restricted to ''E''. In this case, ''F'' is an extension field of ''E'' and ''E'' is a subfield of ...
of the smallest field ''F'' containing two points on the line, the center of the circle, and the radius of the circle. That is, they are of the form , where , , and are in .
Since the field of constructible points is closed under ''square roots'', it contains all points that can be obtained by a finite sequence of quadratic extensions of the field of complex numbers with rational coefficients. By the above paragraph, one can show that any constructible point can be obtained by such a sequence of extensions. As a corollary of this, one finds that the degree of the minimal polynomial for a constructible point (and therefore of any constructible length) is a power of 2. In particular, any constructible point (or length) is an algebraic number
An algebraic number is a number that is a root of a non-zero polynomial in one variable with integer (or, equivalently, rational) coefficients. For example, the golden ratio, (1 + \sqrt)/2, is an algebraic number, because it is a root of th ...
, though not every algebraic number is constructible; for example, is algebraic but not constructible.
Constructible angles
There is abijection
In mathematics, a bijection, also known as a bijective function, one-to-one correspondence, or invertible function, is a function between the elements of two sets, where each element of one set is paired with exactly one element of the other ...
between the angles that are constructible and the points that are constructible on any constructible circle. The angles that are constructible form an abelian group
In mathematics, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on the order in which they are written. That is, the group operation is comm ...
under addition modulo 2π (which corresponds to multiplication of the points on the unit circle viewed as complex numbers). The angles that are constructible are exactly those whose tangent (or equivalently, sine or cosine) is constructible as a number. For example, the regular heptadecagon (the seventeen-sided regular polygon) is constructible because
:
as discovered by Gauss.
The group of constructible angles is closed under the operation that halves angles (which corresponds to taking square roots in the complex numbers). The only angles of finite order that may be constructed starting with two points are those whose order is either a power of two, or a product of a power of two and a set of distinct Fermat primes. In addition there is a dense set of constructible angles of infinite order.
Relation to complex arithmetic
Given a set of points in theEuclidean plane
In mathematics, the Euclidean plane is a Euclidean space of dimension two. That is, a geometric setting in which two real quantities are required to determine the position of each point ( element of the plane), which includes affine notions ...
, selecting any one of them to be called 0 and another to be called 1, together with an arbitrary choice of orientation allows us to consider the points as a set of complex number
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the fo ...
s.
Given any such interpretation of a set of points as complex numbers, the points constructible using valid straightedge-and-compass constructions alone are precisely the elements of the smallest field containing the original set of points and closed under the complex conjugate and square root
In mathematics, a square root of a number is a number such that ; in other words, a number whose '' square'' (the result of multiplying the number by itself, or ⋅ ) is . For example, 4 and −4 are square roots of 16, because .
...
operations (to avoid ambiguity, we can specify the square root with complex argument less than π). The elements of this field are precisely those that may be expressed as a formula in the original points using only the operations of addition, subtraction, multiplication
Multiplication (often denoted by the Multiplication sign, cross symbol , by the mid-line #Notation and terminology, dot operator , by juxtaposition, or, on computers, by an asterisk ) is one of the four Elementary arithmetic, elementary Op ...
, division, complex conjugate, and square root
In mathematics, a square root of a number is a number such that ; in other words, a number whose '' square'' (the result of multiplying the number by itself, or ⋅ ) is . For example, 4 and −4 are square roots of 16, because .
...
, which is easily seen to be a countable dense subset of the plane. Each of these six operations corresponding to a simple straightedge-and-compass construction. From such a formula it is straightforward to produce a construction of the corresponding point by combining the constructions for each of the arithmetic operations. More efficient constructions of a particular set of points correspond to shortcuts in such calculations.
Equivalently (and with no need to arbitrarily choose two points) we can say that, given an arbitrary choice of orientation, a set of points determines a set of complex ratios given by the ratios of the differences between any two pairs of points. The set of ratios constructible using straightedge and compass from such a set of ratios is precisely the smallest field containing the original ratios and closed under taking complex conjugates and square roots.
For example, the real part, imaginary part and modulus of a point or ratio ''z'' (taking one of the two viewpoints above) are constructible as these may be expressed as
:
:
:
''Doubling the cube'' and ''trisection of an angle'' (except for special angles such as any ''φ'' such that ''φ''/(2) is a rational number
In mathematics, a rational number is a number that can be expressed as the quotient or fraction of two integers, a numerator and a non-zero denominator . For example, is a rational number, as is every integer (e.g. ). The set of all ra ...
with denominator not divisible by 3) require ratios which are the solution to cubic equations, while ''squaring the circle'' requires a transcendental ratio. None of these are in the fields described, hence no straightedge-and-compass construction for these exists.
Impossible constructions
The ancient Greeks thought that the construction problems they could not solve were simply obstinate, not unsolvable. With modern methods, however, these straightedge-and-compass constructions have been shown to be logically impossible to perform. (The problems themselves, however, are solvable, and the Greeks knew how to solve them without the constraint of working only with straightedge and compass.)Squaring the circle
The most famous of these problems,squaring the circle
Squaring the circle is a problem in geometry first proposed in Greek mathematics. It is the challenge of constructing a square with the area of a circle by using only a finite number of steps with a compass and straightedge. The difficul ...
, otherwise known as the quadrature of the circle, involves constructing a square with the same area as a given circle using only straightedge and compass.
Squaring the circle has been proved impossible, as it involves generating a transcendental number
In mathematics, a transcendental number is a number that is not algebraic—that is, not the root of a non-zero polynomial of finite degree with rational coefficients. The best known transcendental numbers are and .
Though only a few classes ...
, that is, . Only certain algebraic number
An algebraic number is a number that is a root of a non-zero polynomial in one variable with integer (or, equivalently, rational) coefficients. For example, the golden ratio, (1 + \sqrt)/2, is an algebraic number, because it is a root of th ...
s can be constructed with ruler and compass alone, namely those constructed from the integers with a finite sequence of operations of addition, subtraction, multiplication, division, and taking square roots. The phrase "squaring the circle" is often used to mean "doing the impossible" for this reason.
Without the constraint of requiring solution by ruler and compass alone, the problem is easily solvable by a wide variety of geometric and algebraic means, and was solved many times in antiquity.
A method which comes very close to approximating the "quadrature of the circle" can be achieved using a Kepler triangle
A Kepler triangle is a special right triangle with edge lengths in geometric progression. The ratio of the progression is \sqrt\varphi where \varphi=(1+\sqrt)/2 is the golden ratio, and the progression can be written: or approximately . Squa ...
.
Doubling the cube
Doubling the cube is the construction, using only a straightedge and compass, of the edge of a cube that has twice the volume of a cube with a given edge. This is impossible because the cube root of 2, though algebraic, cannot be computed from integers by addition, subtraction, multiplication, division, and taking square roots. This follows because its minimal polynomial over the rationals has degree 3. This construction is possible using a straightedge with two marks on it and a compass.Angle trisection
Angle trisection is the construction, using only a straightedge and a compass, of an angle that is one-third of a given arbitrary angle. This is impossible in the general case. For example, the angle 2/5radian
The radian, denoted by the symbol rad, is the unit of angle in the International System of Units (SI) and is the standard unit of angular measure used in many areas of mathematics. The unit was formerly an SI supplementary unit (before that ...
s (72° = 360°/5) can be trisected, but the angle of /3 radian
The radian, denoted by the symbol rad, is the unit of angle in the International System of Units (SI) and is the standard unit of angular measure used in many areas of mathematics. The unit was formerly an SI supplementary unit (before that ...
s (60 °) cannot be trisected. The general trisection problem is also easily solved when a straightedge with two marks on it is allowed (a neusis
In geometry, the neusis (; ; plural: grc, νεύσεις, neuseis, label=none) is a geometric construction method that was used in antiquity by Greek mathematicians.
Geometric construction
The neusis construction consists of fitting a lin ...
construction).
Distance to an ellipse
The line segment from any point in the plane to the nearest point on acircle
A circle is a shape consisting of all points in a plane that are at a given distance from a given point, the centre. Equivalently, it is the curve traced out by a point that moves in a plane so that its distance from a given point is cons ...
can be constructed, but the segment from any point in the plane to the nearest point on an ellipse
In mathematics, an ellipse is a plane curve surrounding two focal points, such that for all points on the curve, the sum of the two distances to the focal points is a constant. It generalizes a circle, which is the special type of ellipse in ...
of positive eccentricity cannot in general be constructed.
Alhazen's problem
In 1997, theOxford
Oxford () is a city in England. It is the county town and only city of Oxfordshire. In 2020, its population was estimated at 151,584. It is north-west of London, south-east of Birmingham and north-east of Bristol. The city is home to the ...
mathematician Peter M. Neumann proved the theorem that there is no ruler-and-compass construction for the general solution of the ancient Alhazen's problem (billiard problem or reflection from a spherical mirror).
Constructing regular polygons
 Some regular polygons (e.g. a
Some regular polygons (e.g. a pentagon
In geometry, a pentagon (from the Greek πέντε ''pente'' meaning ''five'' and γωνία ''gonia'' meaning ''angle'') is any five-sided polygon or 5-gon. The sum of the internal angles in a simple pentagon is 540°.
A pentagon may be sim ...
) are easy to construct with straightedge and compass; others are not. This led to the question: Is it possible to construct all regular polygons with straightedge and compass?
Carl Friedrich Gauss in 1796 showed that a regular 17-sided polygon can be constructed, and five years later showed that a regular ''n''-sided polygon can be constructed with straightedge and compass if the odd prime factor
A prime number (or a prime) is a natural number greater than 1 that is not a product of two smaller natural numbers. A natural number greater than 1 that is not prime is called a composite number. For example, 5 is prime because the only ways ...
s of ''n'' are distinct Fermat primes. Gauss conjecture
In mathematics, a conjecture is a conclusion or a proposition that is proffered on a tentative basis without proof. Some conjectures, such as the Riemann hypothesis (still a conjecture) or Fermat's Last Theorem (a conjecture until proven in ...
d that this condition was also necessary; the conjecture was proven by Pierre Wantzel in 1837.
The first few constructible regular polygons have the following numbers of sides:
: 3, 4, 5, 6, 8, 10, 12, 15, 16, 17, 20, 24, 30, 32, 34, 40, 48, 51, 60, 64, 68, 80, 85, 96, 102, 120, 128, 136, 160, 170, 192, 204, 240, 255, 256, 257, 272...
There are known to be an infinitude of constructible regular polygons with an even number of sides (because if a regular ''n''-gon is constructible, then so is a regular 2''n''-gon and hence a regular 4''n''-gon, 8''n''-gon, etc.). However, there are only 31 known constructible regular ''n''-gons with an odd number of sides.
Constructing a triangle from three given characteristic points or lengths
Sixteen key points of atriangle
A triangle is a polygon with three edges and three vertices. It is one of the basic shapes in geometry. A triangle with vertices ''A'', ''B'', and ''C'' is denoted \triangle ABC.
In Euclidean geometry, any three points, when non- colline ...
are its vertices, the midpoints of its sides, the feet of its altitudes, the feet of its internal angle bisectors, and its circumcenter, centroid, orthocenter, and incenter. These can be taken three at a time to yield 139 distinct nontrivial problems of constructing a triangle from three points. Of these problems, three involve a point that can be uniquely constructed from the other two points; 23 can be non-uniquely constructed (in fact for infinitely many solutions) but only if the locations of the points obey certain constraints; in 74 the problem is constructible in the general case; and in 39 the required triangle exists but is not constructible.
Twelve key lengths of a triangle are the three side lengths, the three altitudes, the three medians
The Medes (Old Persian: ; Akkadian: , ; Ancient Greek: ; Latin: ) were an ancient Iranian people who spoke the Median language and who inhabited an area known as Media between western and northern Iran. Around the 11th century BC, the ...
, and the three angle bisectors. Together with the three angles, these give 95 distinct combinations, 63 of which give rise to a constructible triangle, 30 of which do not, and two of which are underdefined.
Restricted constructions
Various attempts have been made to restrict the allowable tools for constructions under various rules, in order to determine what is still constructible and how it may be constructed, as well as determining the minimum criteria necessary to still be able to construct everything that compass and straightedge can.Constructing with only ruler or only compass
It is possible (according to the Mohr–Mascheroni theorem) to construct anything with just a compass if it can be constructed with a ruler and compass, provided that the given data and the data to be found consist of discrete points (not lines or circles). The truth of this theorem depends on the truth of Archimedes' axiom, which is not first-order in nature. Examples of compass-only constructions include Napoleon's problem. It is impossible to take a square root with just a ruler, so some things that cannot be constructed with a ruler can be constructed with a compass; but (by thePoncelet–Steiner theorem
In the branch of mathematics known as Euclidean geometry, the Poncelet–Steiner theorem is one of several results concerning compass and straightedge constructions having additional restrictions imposed on the traditional rules. This result sta ...
) given a single circle and its center, they can be constructed.
Extended constructions
The ancient Greeks classified constructions into three major categories, depending on the complexity of the tools required for their solution. If a construction used only a straightedge and compass, it was called planar; if it also required one or more conic sections (other than the circle), then it was called solid; the third category included all constructions that did not fall into either of the other two categories. This categorization meshes nicely with the modern algebraic point of view. A complex number that can be expressed using only the field operations and square roots (as described above) has a planar construction. A complex number that includes also the extraction of cube roots has a solid construction. In the language of fields, a complex number that is planar has degree a power of two, and lies in afield extension
In mathematics, particularly in algebra, a field extension is a pair of fields E\subseteq F, such that the operations of ''E'' are those of ''F'' restricted to ''E''. In this case, ''F'' is an extension field of ''E'' and ''E'' is a subfield of ...
that can be broken down into a tower of fields where each extension has degree two. A complex number that has a solid construction has degree with prime factors of only two and three, and lies in a field extension that is at the top of a tower of fields where each extension has degree 2 or 3.
Solid constructions
A point has a solid construction if it can be constructed using a straightedge, compass, and a (possibly hypothetical) conic drawing tool that can draw any conic with already constructed focus, directrix, and eccentricity. The same set of points can often be constructed using a smaller set of tools. For example, using a compass, straightedge, and a piece of paper on which we have the parabola y=x2 together with the points (0,0) and (1,0), one can construct any complex number that has a solid construction. Likewise, a tool that can draw any ellipse with already constructed foci and major axis (think two pins and a piece of string) is just as powerful. The ancient Greeks knew that doubling the cube and trisecting an arbitrary angle both had solid constructions. Archimedes gave a solid construction of the regular 7-gon. The quadrature of the circle does not have a solid construction. A regular ''n''-gon has a solid construction if and only if ''n''=2''a''3''b''''m'' where ''a'' and ''b'' are some non-negative integers and ''m'' is a product of zero or more distinctPierpont prime
In number theory, a Pierpont prime is a prime number of the form
2^u\cdot 3^v + 1\,
for some nonnegative integers and . That is, they are the prime numbers for which is 3-smooth. They are named after the mathematician James Pierpont, who us ...
s (primes of the form 2''r''3''s''+1). Therefore, regular ''n''-gon admits a solid, but not planar, construction if and only if ''n'' is in the sequence
: 7, 9, 13, 14, 18, 19, 21, 26, 27, 28, 35, 36, 37, 38, 39, 42, 45, 52, 54, 56, 57, 63, 65, 70, 72, 73, 74, 76, 78, 81, 84, 90, 91, 95, 97...
The set of ''n'' for which a regular ''n''-gon has no solid construction is the sequence
: 11, 22, 23, 25, 29, 31, 33, 41, 43, 44, 46, 47, 49, 50, 53, 55, 58, 59, 61, 62, 66, 67, 69, 71, 75, 77, 79, 82, 83, 86, 87, 88, 89, 92, 93, 94, 98, 99, 100...
Like the question with Fermat primes, it is an open question as to whether there are an infinite number of Pierpont primes.
Angle trisection
What if, together with the straightedge and compass, we had a tool that could (only) trisect an arbitrary angle? Such constructions are solid constructions, but there exist numbers with solid constructions that cannot be constructed using such a tool. For example, we cannot double the cube with such a tool. On the other hand, every regular n-gon that has a solid construction can be constructed using such a tool.Origami
The mathematical theory of origami is more powerful than straightedge-and-compass construction. Folds satisfying the Huzita–Hatori axioms can construct exactly the same set of points as the extended constructions using a compass and conic drawing tool. Therefore, origami can also be used to solve cubic equations (and hence quartic equations), and thus solve two of the classical problems.Markable rulers
Archimedes
Archimedes of Syracuse (;; ) was a Greek mathematician, physicist, engineer, astronomer, and inventor from the ancient city of Syracuse in Sicily. Although few details of his life are known, he is regarded as one of the leading scientis ...
, Nicomedes Nicomedes may refer to:
*Nicomedes (mathematician), ancient Greek mathematician who discovered the conchoid
*Nicomedes of Sparta, regent during the youth of King Pleistoanax, commanded the Spartan army at the Battle of Tanagra (457 BC)
*Saint Nicom ...
and Apollonius gave constructions involving the use of a markable ruler. This would permit them, for example, to take a line segment, two lines (or circles), and a point; and then draw a line which passes through the given point and intersects the two given lines, such that the distance between the points of intersection equals the given segment. This the Greeks called ''neusis'' ("inclination", "tendency" or "verging"), because the new line ''tends'' to the point.
In this expanded scheme, we can trisect an arbitrary angle (seArchimedes' trisection
or extract an arbitrary cube root (due to Nicomedes). Hence, any distance whose ratio to an existing distance is the solution of a cubic or a quartic equation is constructible. Using a markable ruler, regular polygons with solid constructions, like the heptagon, are constructible; and
John H. Conway
John Horton Conway (26 December 1937 – 11 April 2020) was an English mathematician active in the theory of finite groups, knot theory, number theory, combinatorial game theory and coding theory. He also made contributions to many branches o ...
and Richard K. Guy give constructions for several of them.
The neusis construction is more powerful than a conic drawing tool, as one can construct complex numbers that do not have solid constructions. In fact, using this tool one can solve some quintics that are not solvable using radicals. It is known that one cannot solve an irreducible polynomial of prime degree greater or equal to 7 using the neusis construction, so it is not possible to construct a regular 23-gon or 29-gon using this tool. Benjamin and Snyder proved that it is possible to construct the regular 11-gon, but did not give a construction.E. Benjamin, C. Snyder, "On the construction of the regular hendecagon by marked ruler and compass", ''Mathematical Proceedings of the Cambridge Philosophical Society'', 156 (3), 409 -- 424 (2014). It is still open as to whether a regular 25-gon or 31-gon is constructible using this tool.
Trisect a straight segment
 Given a straight line segment called AB, could this be divided in three new equal segments and in many parts required by the use of intercept theorem
Given a straight line segment called AB, could this be divided in three new equal segments and in many parts required by the use of intercept theorem
Computation of binary digits
In 1998 Simon Plouffe gave a ruler-and-compassalgorithm
In mathematics and computer science, an algorithm () is a finite sequence of rigorous instructions, typically used to solve a class of specific problems or to perform a computation. Algorithms are used as specifications for performing ...
that can be used to compute binary digits of certain numbers.
The algorithm involves the repeated doubling of an angle and becomes physically impractical after about 20 binary digits.
See also
* Carlyle circle *Geometric cryptography *Geometrography *List of interactive geometry software, most of them show straightedge-and-compass constructions *Mathematics of paper folding *Underwood Dudley, a mathematician who has made a sideline of collecting false straightedge-and-compass proofs.References
External links
Regular polygon constructions
by Dr. Math at ''The Math Forum @ Drexel''
Construction with the Compass Only
at ''cut-the-knot''
Angle Trisection by Hippocrates
at ''cut-the-knot'' * {{Authority control Compass and straightedge constructions,