Chiral model

In nuclear physics, the chiral model, introduced by Feza Gürsey in 1960, is a phenomenological model describing effective interactions of mesons in the chiral limit (where the masses of the quarks go to zero), but without necessarily mentioning quarks at all. It is a nonlinear sigma model with the principal homogeneous space of a Lie group $G$ as its target manifold. When the model was originally introduced, this Lie group was the SU(''N''), where ''N'' is the number of quark flavors. The Riemannian metric of the target manifold is given by a positive constant multiplied by the Killing form acting upon the Maurer–Cartan form of SU(''N'').

The internal global symmetry of this model is $G_L \times G_R$, the left and right copies, respectively; where the left copy acts as the left action upon the target space, and the right copy acts as the right action. Phenomenologically, the left copy represents flavor rotations among the left-handed quarks, while the right copy describes rotations among the right-handed quarks, while these, L and R, are completely independent of each other. The axial pieces of these symmetries are spontaneously broken so that the corresponding scalar fields are the requisite Nambu−Goldstone bosons.

The model was later studied in the two-dimensional case as an integrable system, in particular an integrable field theory. Its integrability was shown by Faddeev and Reshetikhin in 1982 through the quantum inverse scattering method. The two-dimensional principal chiral model exhibits signatures of integrability such as a Lax pair/zero-curvature formulation, an infinite number of symmetries, and an underlying quantum group symmetry (in this case, Yangian symmetry).

This model admits topological solitons called skyrmions.

Departures from exact chiral symmetry are dealt with in chiral perturbation theory.

Mathematical formulation

On a manifold (considered as the spacetime) and a choice of compact Lie group , the field content is a function $U: M \rightarrow G$. This defines a related field $j_\mu = U^\partial_\mu U$, a $\mathfrak$-valued vector field (really, covector field) which is the Maurer–Cartan form. The principal chiral model is defined by the Lagrangian density
$\mathcal = \frac\mathrm(\partial_\mu U^ \partial^\mu U) = -\frac\mathrm(j_\mu j^\mu),$
where $\kappa$ is a dimensionless coupling. In differential-geometric language, the field $U$ is a section of a principal bundle $\pi: P \rightarrow M$ with fibres isomorphic to the principal homogeneous space for (hence why this defines the ''principal'' chiral model).

Phenomenology

An outline of the original, 2-flavor model

The chiral model of Gürsey (1960; also see Gell-Mann and Lévy) is now appreciated to be an effective theory of QCD with two light quarks, ''u'', and ''d''. The QCD Lagrangian is approximately invariant under independent global flavor rotations of the left- and right-handed quark fields,
:$\begin q_\mathsf \mapsto q_\mathsf'= L\ q_\mathsf = \exp q_\mathsf \\ q_\mathsf \mapsto q_\mathsf'= R\ q_\mathsf = \exp q_\mathsf \end$
where denote the Pauli matrices in the flavor space and _R  are the corresponding rotation angles.

The corresponding symmetry group $\ \text(2)_\mathsf \times \text(2)_\mathsf\$ is the chiral group, controlled by the six conserved currents
:$L_\mu^i = \bar q_\mathsf \gamma_\mu \tfrac q_\mathsf , \qquad R_\mu^i = \bar q_\mathsf \gamma_\mu \tfrac q_\mathsf\ ,$
which can equally well be expressed in terms of the vector and axial-vector currents
:$V_\mu^i = L_\mu^i + R_\mu^i, \qquad A_\mu^i = R_\mu^i - L_\mu^i ~.$

The corresponding conserved charges generate the algebra of the chiral group,
: \left Q_^i, Q_^j \right= i \epsilon^ Q_^k \qquad \qquad \left Q_\mathsf^i, Q_\mathsf^j \right= 0,
with or, equivalently,
: \left Q_^i, Q_^j \right= i \epsilon^ Q_V^k, \qquad \left Q_^i, Q_^j \right= i \epsilon^ Q_^k, \qquad \left Q_^i, Q_^j \right= i \epsilon^ Q_A^k.

Application of these commutation relations to hadronic reactions dominated current algebra calculations in the early 1970s.

At the level of hadrons, pseudoscalar mesons, the ambit of the chiral model, the chiral $\ \text(2)_\mathsf \times \text(2)_\mathsf\$ group is spontaneously broken down to $\text(2)_V\ ,$ by the QCD vacuum. That is, it is realized ''nonlinearly'', in the Nambu–Goldstone mode: The annihilate the vacuum, but the ''Q_A'' do not! This is visualized nicely through a geometrical argument based on the fact that the Lie algebra of $\text(2)_\mathsf \times\text(2)_\mathsf\$ is isomorphic to that of SO(4). The unbroken subgroup, realized in the linear Wigner–Weyl mode, is $\ \text(3) \subset \text(4)\$ which is locally isomorphic to SU(2) (V: isospin).

To construct a non-linear realization of SO(4), the representation describing four-dimensional rotations of a vector
:$\begin \\ \sigma \end \equiv \begin \pi_1 \\ \pi_2 \\ \pi_3 \\ \sigma \end,$
for an infinitesimal rotation parametrized by six angles
:$\left \, \qquad i =1, 2, 3,$
is given by
: \begin \\ \sigma \end \stackrel \begin \\ \sigma' \end = \left \mathbf_4+ \sum_^3 \theta_i^V\ V_i + \sum_^3 \theta_i^A\ A_i \right\begin \\ \sigma \end
where
:$\sum_^3 \theta_i^V\ V_i =\begin 0 & -\theta^V_3 & \theta^V_2 & 0 \\ \theta^V_3 & 0 & -\theta_1^V & 0 \\ -\theta^V_2 & \theta_1^V & 0 & 0 \\ 0 & 0 & 0 & 0 \end \qquad \qquad \sum_^3 \theta_i^A\ A_i = \begin 0 & 0 & 0 & \theta^A_1 \\ 0 & 0 & 0 & \theta^A_2 \\ 0 & 0 & 0 & \theta^A_3 \\ -\theta^A_1 & -\theta_2^A & -\theta_3^A & 0 \end.$

The four real quantities define the smallest nontrivial chiral multiplet and represent the field content of the linear sigma model.

To switch from the above linear realization of SO(4) to the nonlinear one, we observe that, in fact, only three of the four components of are independent with respect to four-dimensional rotations. These three independent components
correspond to coordinates on a hypersphere S³, where and are subjected to the constraint
:$^2 + \sigma^2 = F^2\ ,$
with a pion decay constant with dimension = ''mass''.

Utilizing this to eliminate yields the following transformation properties of under SO(4),
:$\begin \theta^V : \boldsymbol \mapsto \boldsymbol'= \boldsymbol + \boldsymbol^V \times \boldsymbol \\ \theta^A: \boldsymbol \mapsto \boldsymbol'= \boldsymbol + \boldsymbol^A \sqrt \end \qquad \boldsymbol^ \equiv \left \, \qquad i =1, 2, 3.$

The nonlinear terms (shifting ) on the right-hand side of the second equation underlie the nonlinear realization of SO(4). The chiral group $\ \text(2)_\mathsf \times \text(2)_\mathsf \simeq \text(4)\$ is realized nonlinearly on the triplet of pions – which, however, still transform linearly under isospin $\ \text(2)_V \simeq \text(3)\$ rotations parametrized through the angles $\ \left\ ~.$ By contrast, the $\ \left\\$ represent the nonlinear "shifts" (spontaneous breaking).

Through the spinor map, these four-dimensional rotations of can also be conveniently written using 2×2 matrix notation by introducing the unitary matrix
:$U = \frac \left( \sigma \mathbf_2 + i \boldsymbol \cdot \boldsymbol \right)\ ,$
and requiring the transformation properties of under chiral rotations to be
:$U \longrightarrow U' = L U R^\dagger\ ,$
where $~ \theta_\mathsf = \theta_V - \theta_A\ , \quad \theta_\mathsf = \theta_V+ \theta_A ~.$

The transition to the nonlinear realization follows,
:$U = \frac \left( \sqrt\ \mathbf_2 + i \boldsymbol \cdot \boldsymbol \right)\ , \qquad \mathcal_\pi^ = \tfracF^2\ \langle\ \partial_\mu U\ \partial^\mu U^\dagger\ \rangle_\mathsf\ ,$
where $\ \langle \ldots \rangle_\mathsf\$ denotes the trace in the flavor space. This is a non-linear sigma model.

Terms involving $\textstyle\ \partial_\mu \partial^\mu\ U\$ or $\textstyle\ \partial_\mu \partial^\mu\ U^\dagger\$ are not independent and can be brought to this form through partial integration.
The constant ² is chosen in such a way that the Lagrangian matches the usual free term for massless scalar fields when written in terms of the pions,
:$\ \mathcal_\pi^ = \frac \partial_\mu \boldsymbol \cdot \partial^\mu \boldsymbol + \frac \left( \frac \right)^2 + \mathcal ( \pi^6 ) ~.$

Alternate Parametrization

An alternative, equivalent (Gürsey, 1960), parameterization
:$\boldsymbol\mapsto \boldsymbol~ \frac,$
yields a simpler expression for ''U'',
:$U=\mathbf \cos , \pi/F, + i \widehat\cdot \boldsymbol \sin , \pi/F, =e^.$

Note the reparameterized transform under
:$L U R^\dagger=\exp(i\boldsymbol_A\cdot \boldsymbol/2 -i\boldsymbol_V\cdot \boldsymbol/2 ) \exp(i\boldsymbol\cdot \boldsymbol/F ) \exp(i\boldsymbol_A\cdot \boldsymbol/2 +i\boldsymbol_V\cdot \boldsymbol/2 )$
so, then, manifestly identically to the above under isorotations, ; and similarly to the above, as
:$\boldsymbol \longrightarrow \boldsymbol +\boldsymbol_A F+ \cdots =\boldsymbol +\boldsymbol_A F ( , \pi/F, \cot , \pi/F, )$
under the broken symmetries, , the shifts. This simpler expression generalizes readily (Cronin, 1967) to light quarks, so $\textstyle \text(N)_L \times \text(N)_R/\text(N)_V.$

Integrability

Integrable chiral model

Introduced by Richard S. Ward, the integrable chiral model or Ward model is described in terms of a matrix-valued field $J: \mathbb^3 \rightarrow U(n)$ and is given by the partial differential equation
\partial_t(J^J_t)- \partial_x(J^J_x) - \partial_y(J^J_y) - ^J_t, J^J_y= 0.
It has a Lagrangian formulation with the expected kinetic term together with a term which resembles a Wess–Zumino–Witten term. It also has a formulation which is formally identical to the Bogomolny equations but with Lorentz signature. The relation between these formulations can be found in .

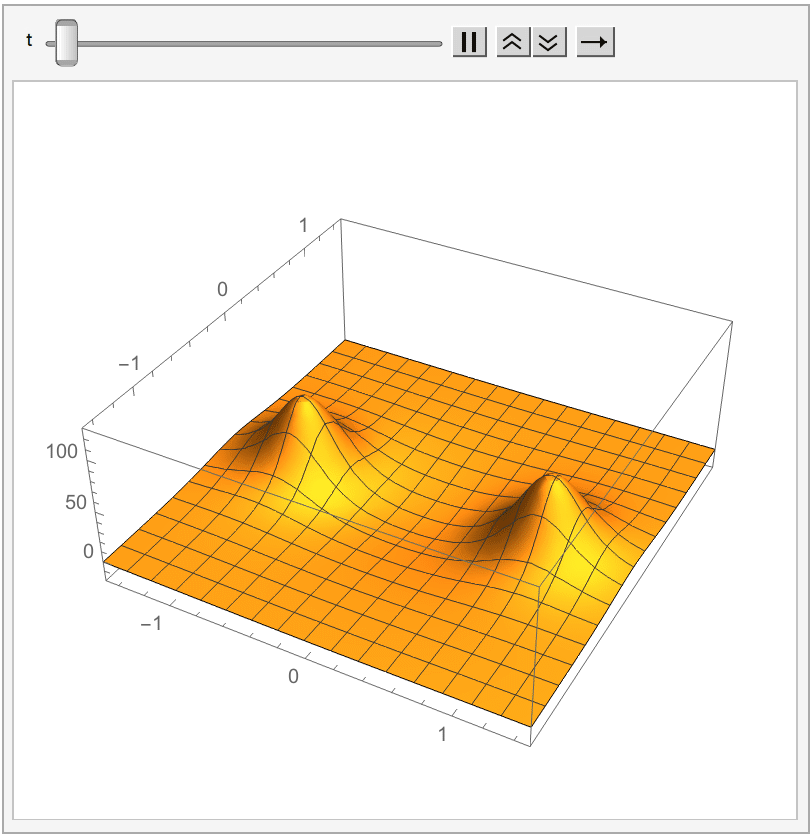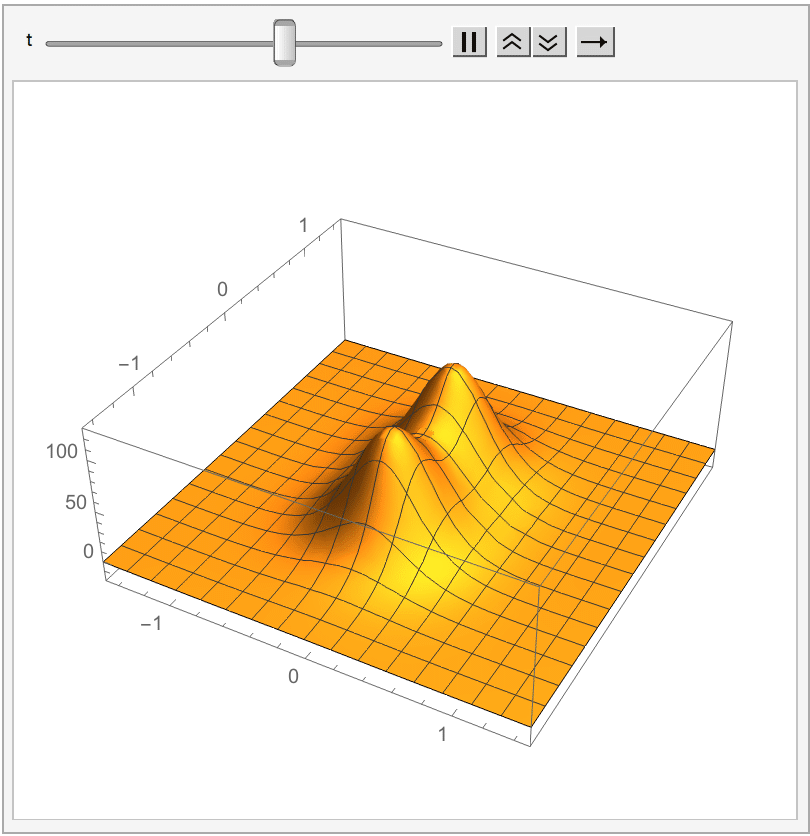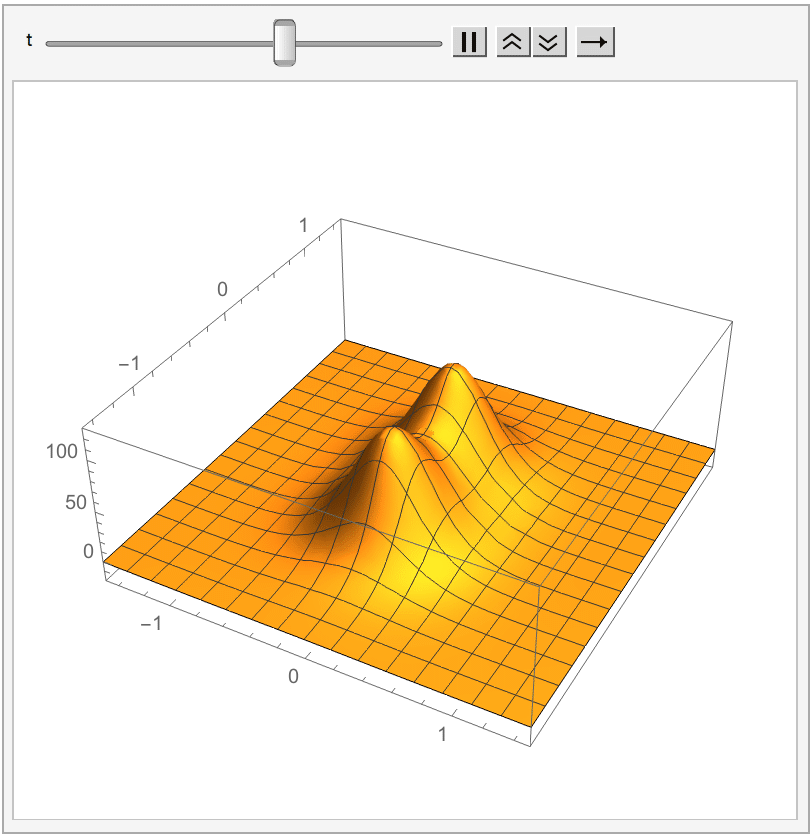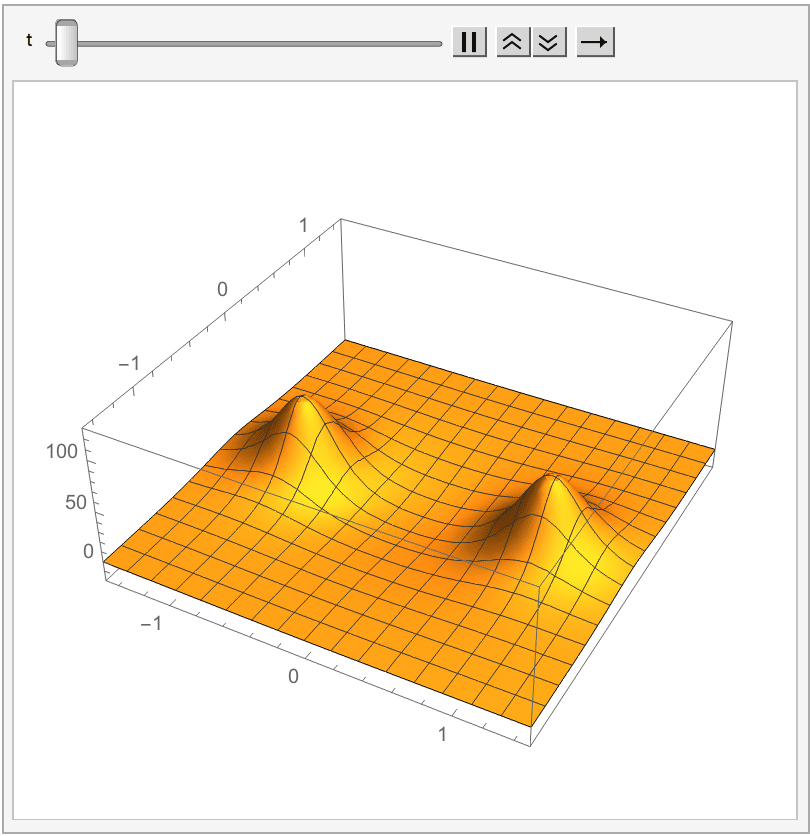
Many exact solutions are known.

Two-dimensional principal chiral model

Here the underlying manifold $M$ is taken to be a Riemann surface, in particular the cylinder $\mathbb^*$ or plane $\mathbb$, conventionally given ''real'' coordinates $\tau, \sigma$, where on the cylinder $\sigma \sim \sigma + 2\pi$ is a periodic coordinate. For application to string theory, this cylinder is the world sheet swept out by the closed string.

Global symmetries

The global symmetries act as internal symmetries on the group-valued field $g(x)$ as $\rho_L(g') g(x) = g'g(x)$ and $\rho_R(g) g(x) = g(x)g'$. The corresponding conserved currents from Noether's theorem are
$L_\alpha = g^\partial_\alpha g, \qquad R_\alpha = \partial_\alpha g g^.$
The equations of motion turn out to be equivalent to conservation of these currents,
$\partial_\alpha L^\alpha = \partial_\alpha R^\alpha = 0, ~ \text ~d * L = d * R = 0.$
The currents additionally satisfy the flatness condition,
dL + \frac ,L= 0 ~~~\text ~~~\partial_\alpha L_\beta - \partial_\beta L_\alpha + _\alpha, L_\beta= 0,
and therefore the equations of motion can be formulated entirely in terms of the currents.

Upon quantization, the axial combination of these currents develop chiral anomalies, summarized in the above-mentioned topological WZWN term.

Lax formulation

Consider the worldsheet in light-cone coordinates $x^\pm = t \pm x$. The components of the appropriate Lax matrix are
$L_\pm(x^+, x^-; \lambda) = \frac.$
The requirement that the zero-curvature condition on $L_\pm$ for all $\lambda$ is equivalent to the conservation of current and flatness of the current $j = (j_+, j_-)$, that is, the equations of motion from the principal chiral model (PCM).

See also

* Sigma model
* Chirality (physics)

References

*
*
*;
*Georgi, H. (1984, 2009). ''Weak Interactions and Modern Particle Theory'' (Dover Books on Physics)
online
.
*
*
*

{{Integrable systems

Quantum field theory
Quantum chromodynamics
Nuclear physics