Cassegrain reflector

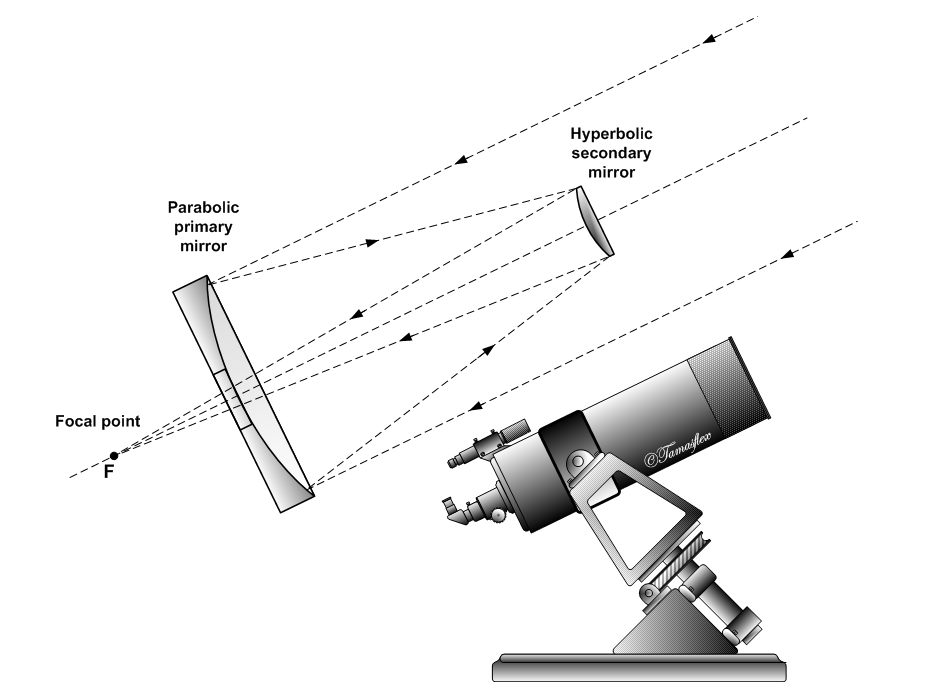The Cassegrain reflector is a combination of a primary concave mirror and a secondary convex mirror, often used in optical telescopes and radio antennas, the main characteristic being that the optical path folds back onto itself, relative to the optical system's primary mirror entrance aperture. This design puts the focal point at a convenient location behind the primary mirror and the convex secondary adds a telephoto effect creating a much longer focal length in a mechanically short system.

In a symmetrical Cassegrain both mirrors are aligned about the optical axis, and the primary mirror usually contains a hole in the center, thus permitting the light to reach an eyepiece, a camera, or an image sensor. Alternatively, as in many radio telescopes, the final focus may be in front of the primary. In an asymmetrical Cassegrain, the mirror(s) may be tilted to avoid obscuration of the primary or to avoid the need for a hole in the primary mirror (or both).

The classic Cassegrain configuration uses a parabolic reflector as the primary while the secondary mirror is hyperbolic. Modern variants may have a hyperbolic primary for increased performance (for example, the Ritchey–Chrétien design); and either or both mirrors may be spherical or elliptical for ease of manufacturing.

The Cassegrain reflector is named after a published reflecting telescope design that appeared in the April 25, 1672 '' Journal des sçavans'' which has been attributed to Laurent Cassegrain. Similar designs using convex secondary mirrors have been found in the Bonaventura Cavalieri's 1632 writings describing burning mirrors and Marin Mersenne's 1636 writings describing telescope designs. James Gregory's 1662 attempts to create a reflecting telescope included a Cassegrain configuration, judging by a convex secondary mirror found among his experiments.

The Cassegrain design is also used in catadioptric systems.

Cassegrain designs

"Classic" Cassegrain telescopes

The "classic" Cassegrain has a parabolic primary mirror and a hyperbolic secondary mirror that reflects the light back down through a hole in the primary. Folding the optics makes this a compact design. On smaller telescopes, and camera lenses, the secondary is often mounted on an optically flat, optically clear glass plate that closes the telescope tube. This support eliminates the "star-shaped" diffraction effects caused by a straight-vaned support spider. The closed tube stays clean, and the primary is protected, at the cost of some loss of light-gathering power.

It makes use of the special properties of parabolic and hyperbolic reflectors. A concave parabolic reflector will reflect all incoming light rays parallel to its axis of symmetry to a single point, the focus. A convex hyperbolic reflector has two foci and will reflect all light rays directed at one of its two foci towards its other focus. The mirrors in this type of telescope are designed and positioned so that they share one focus and so that the second focus of the hyperbolic mirror will be at the same point at which the image is to be observed, usually just outside the eyepiece. The parabolic mirror reflects parallel light rays entering the telescope to its focus, which is also the focus of the hyperbolic mirror. The hyperbolic mirror then reflects those light rays to its other focus, where the image is observed.

In most Cassegrain systems, the secondary mirror blocks a central portion of the aperture. This ring-shaped entrance aperture significantly reduces a portion of the modulation transfer function (MTF) over a range of low spatial frequencies, compared to a full-aperture design such as a refractor or an offset Cassegrain. This MTF notch has the effect of lowering image contrast when imaging broad features. In addition, the support for the secondary (the spider) may introduce diffraction spikes in images.

The radii of curvature of the primary and secondary mirrors, respectively, in the classic configuration are

:$R_1 = -\frac = -\frac$
and
:$R_2 = -\frac = -\frac$

where
* $F$ is the effective focal length of the system,
* $B$ is the back focal length (the distance from the secondary to the focus),
* $D$ is the distance between the two mirrors and
* $M=(F-B)/D$ is the secondary magnification.

If, instead of $B$ and $D$, the known quantities are the focal length of the primary mirror, $f_1$, and the distance to the focus behind the primary mirror, $b$, then $D = f_1(F - b)/(F + f_1)$ and $B = D + b$.

The conic constant of the primary mirror is that of a parabola, $K_1 = -1$. Thanks to that there is no spherical aberration introduced by the primary mirror. The secondary mirror, however, is of a hyperbolic shape with one focus coinciding with that of the primary mirror and the other focus being at the back focal length $B$. Thus, the classical Cassegrain has ideal focus for the chief ray (the center spot diagram is one point). We have,

:$K_2 = -1 - \alpha - \sqrt$,

where
:\alpha = \frac\left \frac\right^2.

Actually, as the conic constants should not depend on scaling, the formulae for both $\alpha$ and $K_2$ can be greatly simplified and presented only as functions of the secondary magnification. Finally,

:$\alpha = \frac$

and

:$K_2 = -1 - \frac = -\left(\frac\right)^2$.

Ritchey-Chrétien

The Ritchey-Chrétien is a specialized Cassegrain reflector which has two hyperbolic mirrors (instead of a parabolic primary). It is free of coma and spherical aberration at a flat focal plane, making it well suited for wide field and photographic observations. It was invented by George Willis Ritchey and Henri Chrétien in the early 1910s. This design is very common in large professional research telescopes, including the Hubble Space Telescope, the Keck Telescopes, and the Very Large Telescope (VLT); it is also found in high-grade amateur telescopes.

Dall-Kirkham

The Dall-Kirkham Cassegrain telescope design was created by Horace Dall in 1928 and took on the name in an article published in ''Scientific American'' in 1930 following discussion between amateur astronomer Allan Kirkham and Albert G. Ingalls, the magazine's astronomy editor at the time. It uses a concave elliptical primary mirror and a convex spherical secondary. While this system is easier to polish than a classic Cassegrain or Ritchey-Chretien system, the off-axis coma is significantly worse, so the image degrades quickly off-axis. Because this is less noticeable at longer focal ratios, Dall-Kirkhams are seldom faster than f/15.

Off-axis configurations

An unusual variant of the Cassegrain is the '' Schiefspiegler'' telescope ("skewed" or "oblique reflector"; also known as the "Kutter telescope" after its inventor, Anton Kutter) which uses tilted mirrors to avoid the secondary mirror casting a shadow on the primary. However, while eliminating diffraction patterns this leads to several other aberrations that must be corrected.

Several different off-axis configurations are used for radio antennas.

Another off-axis, unobstructed design and variant of the Cassegrain is the ' Yolo' reflector invented by Arthur Leonard. This design uses a spherical or parabolic primary and a mechanically warped spherical secondary to correct for off-axis induced astigmatism. When set up correctly the Yolo can give uncompromising unobstructed views of planetary objects and non-wide field targets, with no lack of contrast or image quality caused by spherical aberration. The lack of obstruction also eliminates the diffraction associated with Cassegrain and Newtonian reflector astrophotography.

Catadioptric Cassegrains

Catadioptric Cassegrains use two mirrors, often with a spherical primary mirror to reduce cost, combined with refractive corrector element(s) to correct the resulting aberrations.

Schmidt-Cassegrain

The Schmidt-Cassegrain was developed from the wide-field Schmidt camera, although the Cassegrain configuration gives it a much narrower field of view. The first optical element is a Schmidt corrector plate. The plate is figured by placing a vacuum on one side, and grinding the exact correction required to correct the spherical aberration caused by the spherical primary mirror. Schmidt-Cassegrains are popular with amateur astronomers. An early Schmidt-Cassegrain camera was patented in 1946 by artist/architect/physicist Roger Hayward, with the film holder placed outside the telescope.

Maksutov-Cassegrain

The Maksutov-Cassegrain is a variation of the Maksutov telescope named after the Soviet/Russian optician and astronomer Dmitri Dmitrievich Maksutov. It starts with an optically transparent corrector lens that is a section of a hollow sphere. It has a spherical primary mirror, and a spherical secondary that is usually a mirrored section of the corrector lens.

Argunov-Cassegrain

In the Argunov-Cassegrain telescope all optics are spherical, and the classical Cassegrain secondary mirror is replaced by a sub-aperture corrector consisting of three air spaced lens elements. The element farthest from the primary mirror is a Mangin mirror, which acts as a secondary mirror.

Klevtsov-Cassegrain

The Klevtsov-Cassegrain, like the Argunov-Cassegrain, uses a sub-aperture corrector consisting of a small meniscus lens and a Mangin mirror as its "secondary mirror".New optical systems for small-size telescopes
/ref>

Cassegrain radio antennas

Cassegrain designs are also utilized in satellite telecommunication earth station antennas and radio telescopes, ranging in size from 2.4 metres to 70 metres. The centrally located sub-reflector serves to focus radio frequency signals in a similar fashion to optical telescopes.

An example of a cassegrain radio antenna is the 70-meter dish at JPL's Goldstone antenna complex. For this antenna, the final focus is in front of the primary, at the top of the pedestal protruding from the mirror.

See also

* Catadioptric system
* Celestron (Schmidt–Cassegrains, Maksutov Cassegrains)
* List of telescope types
* Meade Instruments (Schmidt–Cassegrains, Maksutov Cassegrains)
* Questar (Maksutov Cassegrains)
* Refracting telescope
* Vixen (Cassegrains, Klevtsov–Cassegrain)

References

External links

* {{Commons category inline

Antennas (radio)
Radio frequency propagation
Radio frequency antenna types
Telescope types