Calculus of moving surfaces on:
[Wikipedia]
[Google]
[Amazon]
 The calculus of moving surfaces (CMS) is an extension of the classical
The calculus of moving surfaces (CMS) is an extension of the classical  Suppose that is the evolution of the
Suppose that is the evolution of the 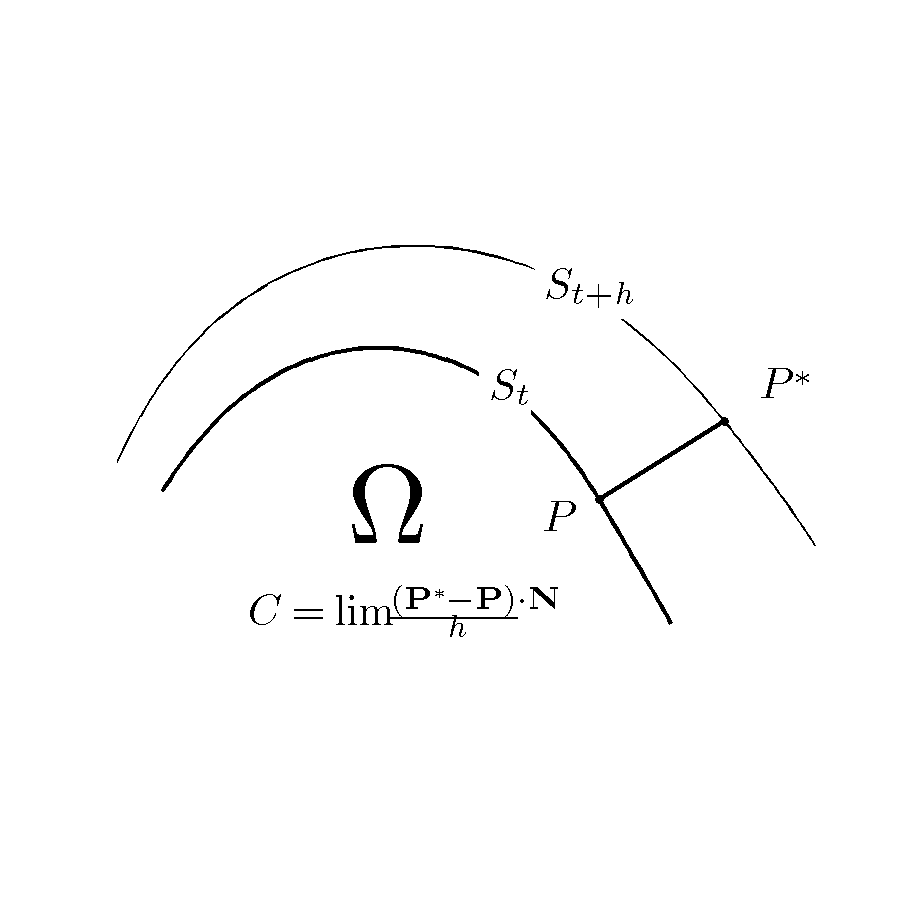
 The Tensorial Time Derivative for a scalar field F defined on is the rate of change in in the instantaneously normal direction:
:
This definition is also illustrated in second geometric figure.
The above definitions are '' geometric''. In analytical settings, direct application of these definitions may not be possible. The CMS gives ''analytical'' definitions of C and in terms of elementary operations from
The Tensorial Time Derivative for a scalar field F defined on is the rate of change in in the instantaneously normal direction:
:
This definition is also illustrated in second geometric figure.
The above definitions are '' geometric''. In analytical settings, direct application of these definitions may not be possible. The CMS gives ''analytical'' definitions of C and in terms of elementary operations from
 The calculus of moving surfaces (CMS) is an extension of the classical
The calculus of moving surfaces (CMS) is an extension of the classical tensor calculus
In mathematics, tensor calculus, tensor analysis, or Ricci calculus is an extension of vector calculus to tensor fields (tensors that may vary over a manifold, e.g. in spacetime).
Developed by Gregorio Ricci-Curbastro and his student Tullio Levi ...
to deforming manifolds. Central to the CMS is the Tensorial Time Derivative whose original definition J. Hadamard, Leçons Sur La Propagation Des Ondes Et Les Équations de l'Hydrodynamique. Paris: Hermann, 1903. was put forth by Jacques Hadamard
Jacques Salomon Hadamard (; 8 December 1865 – 17 October 1963) was a French mathematician who made major contributions in number theory, complex analysis, differential geometry and partial differential equations.
Biography
The son of a teac ...
. It plays the role analogous to that of the covariant derivative on differential manifolds in that it produces a tensor
In mathematics, a tensor is an algebraic object that describes a multilinear relationship between sets of algebraic objects related to a vector space. Tensors may map between different objects such as vectors, scalars, and even other tensor ...
when applied to a tensor.
 Suppose that is the evolution of the
Suppose that is the evolution of the surface
A surface, as the term is most generally used, is the outermost or uppermost layer of a physical object or space. It is the portion or region of the object that can first be perceived by an observer using the senses of sight and touch, and is ...
indexed by a time-like parameter . The definitions of the surface velocity
Velocity is the directional speed of an object in motion as an indication of its rate of change in position as observed from a particular frame of reference and as measured by a particular standard of time (e.g. northbound). Velocity i ...
and the operator are the geometric foundations of the CMS. The velocity C is the rate of deformation of the surface in the instantaneous normal Normal(s) or The Normal(s) may refer to:
Film and television
* ''Normal'' (2003 film), starring Jessica Lange and Tom Wilkinson
* ''Normal'' (2007 film), starring Carrie-Anne Moss, Kevin Zegers, Callum Keith Rennie, and Andrew Airlie
* ''Norma ...
direction. The value of at a point is defined as the limit
:
where is the point on that lies on the straight line perpendicular to at point P. This definition is illustrated in the first geometric figure below. The velocity is a signed quantity: it is positive when points in the direction of the chosen normal, and negative otherwise. The relationship between and is analogous to the relationship between location and velocity in elementary calculus: knowing either quantity allows one to construct the other by differentiation or integration.

 The Tensorial Time Derivative for a scalar field F defined on is the rate of change in in the instantaneously normal direction:
:
This definition is also illustrated in second geometric figure.
The above definitions are '' geometric''. In analytical settings, direct application of these definitions may not be possible. The CMS gives ''analytical'' definitions of C and in terms of elementary operations from
The Tensorial Time Derivative for a scalar field F defined on is the rate of change in in the instantaneously normal direction:
:
This definition is also illustrated in second geometric figure.
The above definitions are '' geometric''. In analytical settings, direct application of these definitions may not be possible. The CMS gives ''analytical'' definitions of C and in terms of elementary operations from calculus
Calculus, originally called infinitesimal calculus or "the calculus of infinitesimals", is the mathematical study of continuous change, in the same way that geometry is the study of shape, and algebra is the study of generalizations of arithm ...
and differential geometry.
Analytical definitions
For analytical definitions of and , consider the evolution of given by : where are general curvilinear space coordinates and are the surface coordinates. By convention, tensor indices of function arguments are dropped. Thus the above equations contains rather than . The velocity object is defined as the partial derivative : The velocity can be computed most directly by the formula : where are the covariant components of the normal vector . Also, defining the shift tensor representation of the Surface's Tangent Space and the Tangent Velocity as , then the definition of the derivative for an invariant ''F'' reads : where is the covariant derivative on S. For ''tensors'', an appropriate generalization is needed. The proper definition for a representative tensor reads : where areChristoffel symbols
In mathematics and physics, the Christoffel symbols are an array of numbers describing a metric connection. The metric connection is a specialization of the affine connection to surfaces or other manifolds endowed with a metric, allowing distanc ...
and is the surface's appropriate temporal symbols ( is a matrix representation of the surface's curvature shape operator)
Properties of the -derivative
The -derivative commutes with contraction, satisfies theproduct rule
In calculus, the product rule (or Leibniz rule or Leibniz product rule) is a formula used to find the derivatives of products of two or more functions. For two functions, it may be stated in Lagrange's notation as (u \cdot v)' = u ' \cdot v ...
for any collection of indices
:
and obeys a chain rule
In calculus, the chain rule is a formula that expresses the derivative of the composition of two differentiable functions and in terms of the derivatives of and . More precisely, if h=f\circ g is the function such that h(x)=f(g(x)) for every , ...
for surface restrictions of spatial tensors:
:
Chain rule shows that the -derivatives of spatial "metrics" vanishes
:
where and are covariant and contravariant metric tensors, is the Kronecker delta
In mathematics, the Kronecker delta (named after Leopold Kronecker) is a function of two variables, usually just non-negative integers. The function is 1 if the variables are equal, and 0 otherwise:
\delta_ = \begin
0 &\text i \neq j, \\
1 & ...
symbol, and and are the Levi-Civita symbol
In mathematics, particularly in linear algebra, tensor analysis, and differential geometry, the Levi-Civita symbol or Levi-Civita epsilon represents a collection of numbers; defined from the parity of a permutation, sign of a permutation of the n ...
s. The main article on Levi-Civita symbols describes them for Cartesian coordinate systems
A Cartesian coordinate system (, ) in a plane is a coordinate system that specifies each point uniquely by a pair of numerical coordinates, which are the signed distances to the point from two fixed perpendicular oriented lines, measured in ...
. The preceding rule is valid in general coordinates, where the definition of the Levi-Civita symbols must include the square root of the determinant
In mathematics, the determinant is a scalar value that is a function of the entries of a square matrix. It characterizes some properties of the matrix and the linear map represented by the matrix. In particular, the determinant is nonzero if a ...
of the covariant metric tensor .
Differentiation table for the -derivative
The derivative of the key surface objects leads to highly concise and attractive formulas. When applied to the covariant surface metric tensor and the contravariant metric tensor , the following identities result : where and are the doubly covariant and doubly contravariant curvature tensors. These curvature tensors, as well as for the mixed curvature tensor , satisfy : The shift tensor and the normal satisfy : Finally, the surfaceLevi-Civita symbol
In mathematics, particularly in linear algebra, tensor analysis, and differential geometry, the Levi-Civita symbol or Levi-Civita epsilon represents a collection of numbers; defined from the parity of a permutation, sign of a permutation of the n ...
s and satisfy
:
Time differentiation of integrals
The CMS provides rules for time differentiation of volume and surface integrals.References
{{Reflist Tensors Differential geometry Riemannian geometry Curvature (mathematics) Calculus