BeltramiŌĆōKlein model on:
[Wikipedia]
[Google]
[Amazon]

 In geometry, the BeltramiŌĆōKlein model, also called the projective model, Klein disk model, and the CayleyŌĆōKlein model, is a model of
In geometry, the BeltramiŌĆōKlein model, also called the projective model, Klein disk model, and the CayleyŌĆōKlein model, is a model of
 While lines in the hyperbolic plane are easy to draw in the Klein disk model, it is not the same with circles, hypercycles and
While lines in the hyperbolic plane are easy to draw in the Klein disk model, it is not the same with circles, hypercycles and
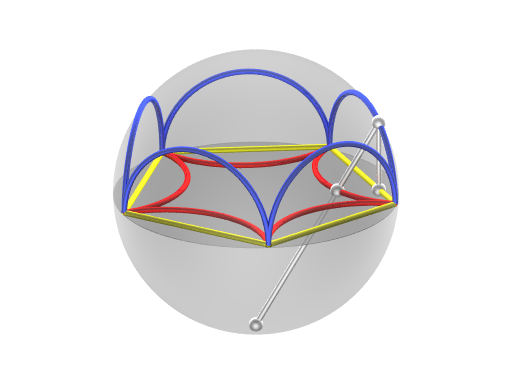
 Both the
Both the
 Given two distinct points ''U'' and ''V'' in the open unit ball of the model in
Given two distinct points ''U'' and ''V'' in the open unit ball of the model in answer
from
 The
The
 In geometry, the BeltramiŌĆōKlein model, also called the projective model, Klein disk model, and the CayleyŌĆōKlein model, is a model of
In geometry, the BeltramiŌĆōKlein model, also called the projective model, Klein disk model, and the CayleyŌĆōKlein model, is a model of hyperbolic geometry
In mathematics, hyperbolic geometry (also called Lobachevskian geometry or BolyaiŌĆōLobachevskian geometry) is a non-Euclidean geometry. The parallel postulate of Euclidean geometry is replaced with:
:For any given line ''R'' and point ''P ...
in which points are represented by the points in the interior of the unit disk
In mathematics, the open unit disk (or disc) around ''P'' (where ''P'' is a given point in the plane), is the set of points whose distance from ''P'' is less than 1:
:D_1(P) = \.\,
The closed unit disk around ''P'' is the set of points whose d ...
(or ''n''-dimensional unit ball
Unit may refer to:
Arts and entertainment
* UNIT, a fictional military organization in the science fiction television series ''Doctor Who''
* Unit of action, a discrete piece of action (or beat) in a theatrical presentation
Music
* ''Unit'' (a ...
) and lines are represented by the chords, straight line segments with ideal endpoints on the boundary sphere
A sphere () is a geometrical object that is a three-dimensional analogue to a two-dimensional circle. A sphere is the set of points that are all at the same distance from a given point in three-dimensional space.. That given point is the c ...
.
The BeltramiŌĆōKlein model is named after the Italian geometer Eugenio Beltrami and the German Felix Klein
Christian Felix Klein (; 25 April 1849 ŌĆō 22 June 1925) was a German mathematician and mathematics educator, known for his work with group theory, complex analysis, non-Euclidean geometry, and on the associations between geometry and grou ...
while "Cayley" in CayleyŌĆōKlein model refers to the English geometer Arthur Cayley
Arthur Cayley (; 16 August 1821 ŌĆō 26 January 1895) was a prolific British mathematician who worked mostly on algebra. He helped found the modern British school of pure mathematics.
As a child, Cayley enjoyed solving complex maths problem ...
.
The BeltramiŌĆōKlein model is analogous to the gnomonic projection
A gnomonic map projection is a map projection which displays all great circles as straight lines, resulting in any straight line segment on a gnomonic map showing a geodesic, the shortest route between the segment's two endpoints. This is achi ...
of spherical geometry
300px, A sphere with a spherical triangle on it.
Spherical geometry is the geometry of the two-dimensional surface of a sphere. In this context the word "sphere" refers only to the 2-dimensional surface and other terms like "ball" or "solid sp ...
, in that geodesics
In geometry, a geodesic () is a curve representing in some sense the shortest path ( arc) between two points in a surface, or more generally in a Riemannian manifold. The term also has meaning in any differentiable manifold with a connection. ...
(great circle
In mathematics, a great circle or orthodrome is the circular intersection of a sphere and a plane passing through the sphere's center point.
Any arc of a great circle is a geodesic of the sphere, so that great circles in spherical geome ...
s in spherical geometry) are mapped to straight lines.
This model is not conformal, meaning that angles and circles are distorted, whereas the Poincar├® disk model
In geometry, the Poincar├® disk model, also called the conformal disk model, is a model of 2-dimensional hyperbolic geometry in which all points are inside the unit disk, and straight lines are either circular arcs contained within the disk ...
preserves these.
In this model, lines and segments are straight Euclidean segments, whereas in the Poincar├® disk model
In geometry, the Poincar├® disk model, also called the conformal disk model, is a model of 2-dimensional hyperbolic geometry in which all points are inside the unit disk, and straight lines are either circular arcs contained within the disk ...
, lines are arcs that meet the boundary orthogonal
In mathematics, orthogonality is the generalization of the geometric notion of '' perpendicularity''.
By extension, orthogonality is also used to refer to the separation of specific features of a system. The term also has specialized meanings in ...
ly.
History
This model made its first appearance forhyperbolic geometry
In mathematics, hyperbolic geometry (also called Lobachevskian geometry or BolyaiŌĆōLobachevskian geometry) is a non-Euclidean geometry. The parallel postulate of Euclidean geometry is replaced with:
:For any given line ''R'' and point ''P ...
in two memoirs of Eugenio Beltrami published in 1868, first for dimension and then for general ''n'', these essays proved the equiconsistency
In mathematical logic, two theories are equiconsistent if the consistency of one theory implies the consistency of the other theory, and vice versa. In this case, they are, roughly speaking, "as consistent as each other".
In general, it is not ...
of hyperbolic geometry with ordinary Euclidean geometry
Euclidean geometry is a mathematical system attributed to ancient Greek mathematician Euclid, which he described in his textbook on geometry: the '' Elements''. Euclid's approach consists in assuming a small set of intuitively appealing axioms ...
.
The papers of Beltrami remained little noticed until recently and the model was named after Klein ("The Klein disk model"). This happened as follows. In 1859 Arthur Cayley
Arthur Cayley (; 16 August 1821 ŌĆō 26 January 1895) was a prolific British mathematician who worked mostly on algebra. He helped found the modern British school of pure mathematics.
As a child, Cayley enjoyed solving complex maths problem ...
used the cross-ratio
In geometry, the cross-ratio, also called the double ratio and anharmonic ratio, is a number associated with a list of four collinear points, particularly points on a projective line. Given four points ''A'', ''B'', ''C'' and ''D'' on a line, t ...
definition of angle due to Laguerre to show how Euclidean geometry could be defined using projective geometry
In mathematics, projective geometry is the study of geometric properties that are invariant with respect to projective transformations. This means that, compared to elementary Euclidean geometry, projective geometry has a different setting, ...
. His definition of distance later became known as the Cayley metric.
In 1869, the young (twenty-year-old) Felix Klein
Christian Felix Klein (; 25 April 1849 ŌĆō 22 June 1925) was a German mathematician and mathematics educator, known for his work with group theory, complex analysis, non-Euclidean geometry, and on the associations between geometry and grou ...
became acquainted with Cayley's work. He recalled that in 1870 he gave a talk on the work of Cayley at the seminar of Weierstrass
Karl Theodor Wilhelm Weierstrass (german: link=no, Weierstra├¤ ; 31 October 1815 ŌĆō 19 February 1897) was a German mathematician often cited as the "father of modern analysis". Despite leaving university without a degree, he studied mathematics ...
and he wrote:
:"I finished with a question whether there might exist a connection between the ideas of Cayley and Lobachevsky
Nikolai Ivanovich Lobachevsky ( rus, ąØąĖą║ąŠą╗ą░╠üą╣ ąśą▓ą░╠üąĮąŠą▓ąĖčć ąøąŠą▒ą░č湥╠üą▓čüą║ąĖą╣, p=n╩▓ik╔É╦łlaj ╔¬╦łvan╔Öv╩▓╔¬t╔Ģ l╔Öb╔É╦łt╔Ģ╔øfsk╩▓╔¬j, a=Ru-Nikolai_Ivanovich_Lobachevsky.ogg; ŌĆō ) was a Russian mathematician and geometer, kn ...
. I was given the answer that these two systems were conceptually widely separated."
Later, Felix Klein
Christian Felix Klein (; 25 April 1849 ŌĆō 22 June 1925) was a German mathematician and mathematics educator, known for his work with group theory, complex analysis, non-Euclidean geometry, and on the associations between geometry and grou ...
realized that Cayley's ideas give rise to a projective model of the non-Euclidean plane.
As Klein puts it, "I allowed myself to be convinced by these objections and put aside this already mature idea." However, in 1871, he returned to this idea, formulated it mathematically, and published it.
Distance formula
The distance function for the BeltramiŌĆōKlein model is aCayleyŌĆōKlein metric
In mathematics, a CayleyŌĆōKlein metric is a metric on the complement of a fixed quadric in a projective space which is defined using a cross-ratio. The construction originated with Arthur Cayley's essay "On the theory of distance"Cayley (1859), ...
. Given two distinct points ''p'' and ''q'' in the open unit ball, the unique straight line connecting them intersects the boundary at two ideal point
In hyperbolic geometry, an ideal point, omega point or point at infinity is a well-defined point outside the hyperbolic plane or space.
Given a line ''l'' and a point ''P'' not on ''l'', right- and left- limiting parallels to ''l'' through '' ...
s, ''a'' and ''b'', label them so that the points are, in order, ''a'', ''p'', ''q'', ''b'' and and .
The hyperbolic distance between ''p'' and ''q'' is then:
The vertical bars indicate Euclidean distances between the points in the model, log is the natural logarithm
The natural logarithm of a number is its logarithm to the base of the mathematical constant , which is an irrational and transcendental number approximately equal to . The natural logarithm of is generally written as , , or sometimes, if ...
and the factor of one half is needed to give the model the standard curvature
In mathematics, curvature is any of several strongly related concepts in geometry. Intuitively, the curvature is the amount by which a curve deviates from being a straight line, or a surface deviates from being a plane.
For curves, the can ...
of −1.
When one of the points is the origin and Euclidean distance between the points is ''r'' then the hyperbolic distance is:
:
where ''artanh
In mathematics, the inverse hyperbolic functions are the inverse functions of the hyperbolic functions.
For a given value of a hyperbolic function, the corresponding inverse hyperbolic function provides the corresponding hyperbolic angle. The s ...
'' is the inverse hyperbolic function of the hyperbolic tangent
In mathematics, hyperbolic functions are analogues of the ordinary trigonometric functions, but defined using the hyperbola rather than the circle. Just as the points form a circle with a unit radius, the points form the right half of the ...
.
The Klein disk model
In two dimensions the BeltramiŌĆōKlein model is called the Klein disk model. It is a disk and the inside of the disk is a model of the entirehyperbolic plane
In mathematics, hyperbolic geometry (also called Lobachevskian geometry or BolyaiŌĆō Lobachevskian geometry) is a non-Euclidean geometry. The parallel postulate of Euclidean geometry is replaced with:
:For any given line ''R'' and point ' ...
.
Lines in this model are represented by chords
Chord may refer to:
* Chord (music), an aggregate of musical pitches sounded simultaneously
** Guitar chord a chord played on a guitar, which has a particular tuning
* Chord (geometry), a line segment joining two points on a curve
* Chord ( ...
of the boundary circle (also called the ''absolute Absolute may refer to:
Companies
* Absolute Entertainment, a video game publisher
* Absolute Radio, (formerly Virgin Radio), independent national radio station in the UK
* Absolute Software Corporation, specializes in security and data risk manag ...
'').
The points on the boundary circle are called ideal point
In hyperbolic geometry, an ideal point, omega point or point at infinity is a well-defined point outside the hyperbolic plane or space.
Given a line ''l'' and a point ''P'' not on ''l'', right- and left- limiting parallels to ''l'' through '' ...
s;
although well defined
In mathematics, a well-defined expression or unambiguous expression is an expression whose definition assigns it a unique interpretation or value. Otherwise, the expression is said to be ''not well defined'', ill defined or ''ambiguous''. A func ...
, they do not belong to the hyperbolic plane.
Neither do points outside the disk, which are sometimes called ultra ideal points.
The model is not conformal, meaning that angles
are distorted, and circles on the hyperbolic plane
In mathematics, hyperbolic geometry (also called Lobachevskian geometry or BolyaiŌĆō Lobachevskian geometry) is a non-Euclidean geometry. The parallel postulate of Euclidean geometry is replaced with:
:For any given line ''R'' and point ' ...
are in general not circular in the model.
Only circles that have their centre at the centre of the boundary circle are not distorted. All other circles are distorted, as are horocycle
In hyperbolic geometry, a horocycle (), sometimes called an oricycle, oricircle, or limit circle, is a curve whose normal or perpendicular geodesics all converge asymptotically in the same direction. It is the two-dimensional case of a horosph ...
s and hypercycles
Properties
Chords that meet on the boundary circle arelimiting parallel
In neutral or absolute geometry, and in hyperbolic geometry, there may be many lines parallel to a given line l through a point P not on line R; however, in the plane, two parallels may be closer to l than all others (one in each direction of R) ...
lines.
Two chords are perpendicular if, when extended outside the disk, each goes through the pole
Pole may refer to:
Astronomy
*Celestial pole, the projection of the planet Earth's axis of rotation onto the celestial sphere; also applies to the axis of rotation of other planets
*Pole star, a visible star that is approximately aligned with the ...
of the other. (The pole of a chord is an ultra ideal point: the point outside the disk where the tangents to the disk at the endpoints of the chord meet.)
Chords that go through the centre of the disk have their pole at infinity, orthogonal to the direction of the chord (this implies that right angles on diameters are not distorted).
Compass and straightedge constructions
Here is how one can usecompass and straightedge constructions
In geometry, straightedge-and-compass construction ŌĆō also known as ruler-and-compass construction, Euclidean construction, or classical construction ŌĆō is the construction of lengths, angles, and other geometric figures using only an ideali ...
in the model to achieve the effect of the basic constructions in the hyperbolic plane
In mathematics, hyperbolic geometry (also called Lobachevskian geometry or BolyaiŌĆō Lobachevskian geometry) is a non-Euclidean geometry. The parallel postulate of Euclidean geometry is replaced with:
:For any given line ''R'' and point ' ...
.
* The pole of a line. While the pole is not a point in the hyperbolic plane (it is an ultra ideal point) most constructions will use the pole of a line in one or more ways.
:For a line: construct the tangents to the boundary circle through the ideal (end) points of the line. the point where these tangents intersect is the pole.
:For diameter
In geometry, a diameter of a circle is any straight line segment that passes through the center of the circle and whose endpoints lie on the circle. It can also be defined as the longest chord of the circle. Both definitions are also valid f ...
s of the disk: the pole is at infinity perpendicular to the diameter.
*To construct a perpendicular to a given line through a given point draw the ray
Ray may refer to:
Fish
* Ray (fish), any cartilaginous fish of the superorder Batoidea
* Ray (fish fin anatomy), a bony or horny spine on a fin
Science and mathematics
* Ray (geometry), half of a line proceeding from an initial point
* Ray (gr ...
from the pole of the line through the given point. The part of the ray that is inside the disk is the perpendicular.
: When the line is a diameter of the disk then the perpendicular is the chord that is (Euclidean) perpendicular to that diameter and going through the given point.
* To find the midpoint of given segment : Draw the lines through A and B that are perpendicular to . (see above) Draw the lines connecting the ideal points of these lines, two of these lines will intersect the segment and will do this at the same point. This point is the (hyperbolic) midpoint
In geometry, the midpoint is the middle point of a line segment. It is equidistant from both endpoints, and it is the centroid both of the segment and of the endpoints. It bisects the segment.
Formula
The midpoint of a segment in ''n''-dimen ...
of.
* To bisect a given angle : Draw the ray
Ray may refer to:
Fish
* Ray (fish), any cartilaginous fish of the superorder Batoidea
* Ray (fish fin anatomy), a bony or horny spine on a fin
Science and mathematics
* Ray (geometry), half of a line proceeding from an initial point
* Ray (gr ...
s AB and AC. Draw tangents to the circle where the rays intersect the boundary circle. Draw a line from ''A'' to the point where the tangents intersect. The part of this line between ''A'' and the boundary circle is the bisector.
* The common perpendicular of two lines is the chord that when extended goes through both poles
Poles,, ; singular masculine: ''Polak'', singular feminine: ''Polka'' or Polish people, are a West Slavic nation and ethnic group, who share a common history, culture, the Polish language and are identified with the country of Poland in ...
of the chords.
: When one of the chords is a diameter of the boundary circle then the common perpendicular is the chord that is perpendicular to the diameter and that when lengthened goes through the pole of the other chord.
*To reflect a point P in a line l: From a point R on the line l draw the ray through P. Let X be the ideal point where the ray intersects the absolute. Draw the ray from the pole of line l through X, let Y be another ideal point that intersects the ray. Draw the segment RY. The reflection of point P is the point where the ray from the pole of line l through P intersects RY.
Circles, hypercycles and horocycles
horocycle
In hyperbolic geometry, a horocycle (), sometimes called an oricycle, oricircle, or limit circle, is a curve whose normal or perpendicular geodesics all converge asymptotically in the same direction. It is the two-dimensional case of a horosph ...
s.
Circles (the set of all points in a plane that are at a given distance from a given point, its center) in the model become ellipse
In mathematics, an ellipse is a plane curve surrounding two focal points, such that for all points on the curve, the sum of the two distances to the focal points is a constant. It generalizes a circle, which is the special type of ellipse in ...
s increasingly flattened as they are nearer to the edge. Also angles in the Klein disk model are deformed.
For constructions in the hyperbolic plane that contain circles, hypercycles, horocycles or non right angle
In geometry and trigonometry, a right angle is an angle of exactly 90 degrees or radians corresponding to a quarter turn. If a ray is placed so that its endpoint is on a line and the adjacent angles are equal, then they are right angles. Th ...
s it is better to use the Poincar├® disk model
In geometry, the Poincar├® disk model, also called the conformal disk model, is a model of 2-dimensional hyperbolic geometry in which all points are inside the unit disk, and straight lines are either circular arcs contained within the disk ...
or the Poincar├® half-plane model
In non-Euclidean geometry, the Poincar├® half-plane model is the upper half-plane, denoted below as H = \, together with a metric, the Poincar├® metric, that makes it a model of two-dimensional hyperbolic geometry.
Equivalently the Poincar├ ...
.
Relation to the Poincar├® disk model

 Both the
Both the Poincar├® disk model
In geometry, the Poincar├® disk model, also called the conformal disk model, is a model of 2-dimensional hyperbolic geometry in which all points are inside the unit disk, and straight lines are either circular arcs contained within the disk ...
and the Klein disk model are models of the hyperbolic plane. An advantage of the Poincar├® disk model is that it is conformal (circles and angles are not distorted); a disadvantage is that lines of the geometry are circular arc
Circular may refer to:
* The shape of a circle
* ''Circular'' (album), a 2006 album by Spanish singer Vega
* Circular letter (disambiguation)
** Flyer (pamphlet), a form of advertisement
* Circular reasoning, a type of logical fallacy
* Circular ...
s orthogonal to the boundary circle of the disk.
The two models are related through a projection on or from the hemisphere model. The Klein model is an orthographic projection
Orthographic projection (also orthogonal projection and analemma) is a means of representing three-dimensional objects in two dimensions. Orthographic projection is a form of parallel projection in which all the projection lines are orthogona ...
to the hemisphere model while the Poincar├® disk model is a stereographic projection
In mathematics, a stereographic projection is a perspective projection of the sphere, through a specific point on the sphere (the ''pole'' or ''center of projection''), onto a plane (the ''projection plane'') perpendicular to the diameter thro ...
.
When projecting the same lines in both models on one disk both lines go through the same two ideal point
In hyperbolic geometry, an ideal point, omega point or point at infinity is a well-defined point outside the hyperbolic plane or space.
Given a line ''l'' and a point ''P'' not on ''l'', right- and left- limiting parallels to ''l'' through '' ...
s. (the ideal points remain on the same spot) also the pole
Pole may refer to:
Astronomy
*Celestial pole, the projection of the planet Earth's axis of rotation onto the celestial sphere; also applies to the axis of rotation of other planets
*Pole star, a visible star that is approximately aligned with the ...
of the chord is the centre of the circle that contains the arc.
If P is a point a distance from the centre of the unit circle in the BeltramiŌĆōKlein model, then the corresponding point on the Poincar├® disk model a distance of u on the same radius:
:
Conversely, If P is a point a distance from the centre of the unit circle in the Poincar├® disk model, then the corresponding point of the BeltramiŌĆōKlein model is a distance of s on the same radius:
:
Relation of the disk model to the hyperboloid model
Both thehyperboloid model
In geometry, the hyperboloid model, also known as the Minkowski model after Hermann Minkowski, is a model of ''n''-dimensional hyperbolic geometry in which points are represented by points on the forward sheet ''S''+ of a two-sheeted hyperbo ...
and the Klein disk model are models of the hyperbolic plane.
The Klein disk (K, in the picture) is a gnomonic projection
A gnomonic map projection is a map projection which displays all great circles as straight lines, resulting in any straight line segment on a gnomonic map showing a geodesic, the shortest route between the segment's two endpoints. This is achi ...
of the hyperboloid model (Hy) with as center the center of the hyperboloid (O) and the projection plane tangent to the nearest point of the hyperboloid.
Distance and metric tensor
 Given two distinct points ''U'' and ''V'' in the open unit ball of the model in
Given two distinct points ''U'' and ''V'' in the open unit ball of the model in Euclidean space
Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, that is, in Euclid's ''Elements'', it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are Euclidea ...
, the unique straight line connecting them intersects the unit sphere at two ideal point
In hyperbolic geometry, an ideal point, omega point or point at infinity is a well-defined point outside the hyperbolic plane or space.
Given a line ''l'' and a point ''P'' not on ''l'', right- and left- limiting parallels to ''l'' through '' ...
s ''A'' and ''B'', labeled so that the points are, in order along the line, ''A'', ''U'', ''V'', ''B''. Taking the centre of the unit ball of the model as the origin, and assigning position vectors u, v, a, b respectively to the points ''U'', ''V'', ''A'', ''B'', we have that that and , where denotes the Euclidean norm
Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, that is, in Euclid's ''Elements'', it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are Euclidean ...
. Then the distance between ''U'' and ''V'' in the modelled hyperbolic space is expressed as
:
where the factor of one half is needed to make the curvature
In mathematics, curvature is any of several strongly related concepts in geometry. Intuitively, the curvature is the amount by which a curve deviates from being a straight line, or a surface deviates from being a plane.
For curves, the can ...
−1.
The associated metric tensor
In the mathematical field of differential geometry, a metric tensor (or simply metric) is an additional structure on a manifold (such as a surface) that allows defining distances and angles, just as the inner product on a Euclidean space allow ...
is given byfrom
Stack Exchange
Stack Exchange is a network of question-and-answer (Q&A) websites on topics in diverse fields, each site covering a specific topic, where questions, answers, and users are subject to a reputation award process. The reputation system allows th ...
:
Relation to the hyperboloid model
 The
The hyperboloid model
In geometry, the hyperboloid model, also known as the Minkowski model after Hermann Minkowski, is a model of ''n''-dimensional hyperbolic geometry in which points are represented by points on the forward sheet ''S''+ of a two-sheeted hyperbo ...
is a model of hyperbolic geometry within -dimensional Minkowski space
In mathematical physics, Minkowski space (or Minkowski spacetime) () is a combination of three-dimensional Euclidean space and time into a four-dimensional manifold where the spacetime interval between any two events is independent of the iner ...
. The Minkowski inner product is given by
:
and the norm by . The hyperbolic plane is embedded in this space as the vectors x with and ''x''0 (the "timelike component") positive. The intrinsic distance (in the embedding) between points u and v is then given by
:
This may also be written in the homogeneous form
:
which allows the vectors to be rescaled for convenience.
The BeltramiŌĆōKlein model is obtained from the hyperboloid model by rescaling all vectors so that the timelike component is 1, that is, by projecting the hyperboloid embedding through the origin onto the plane . The distance function, in its homogeneous form, is unchanged. Since the intrinsic lines (geodesics) of the hyperboloid model are the intersection of the embedding with planes through the Minkowski origin, the intrinsic lines of the BeltramiŌĆōKlein model are the chords of the sphere.
Relation to the Poincar├® ball model
Both the Poincar├® ball model and the BeltramiŌĆōKlein model are models of the ''n''-dimensional hyperbolic space in the ''n''-dimensional unit ball in R''n''. If is a vector of norm less than one representing a point of the Poincar├® disk model, then the corresponding point of the BeltramiŌĆōKlein model is given by : Conversely, from a vector of norm less than one representing a point of the BeltramiŌĆōKlein model, the corresponding point of the Poincar├® disk model is given by : Given two points on the boundary of the unit disk, which are traditionally called ''ideal points'', the straight line connecting them in the BeltramiŌĆōKlein model is the chord between them, while in the corresponding Poincar├® model the line is acircular arc
Circular may refer to:
* The shape of a circle
* ''Circular'' (album), a 2006 album by Spanish singer Vega
* Circular letter (disambiguation)
** Flyer (pamphlet), a form of advertisement
* Circular reasoning, a type of logical fallacy
* Circular ...
on the two-dimensional subspace generated by the two boundary point vectors, meeting the boundary of the ball at right angles. The two models are related through a projection from the center of the disk; a ray from the center passing through a point of one model line passes through the corresponding point of the line in the other model.
See also
*Poincar├® half-plane model
In non-Euclidean geometry, the Poincar├® half-plane model is the upper half-plane, denoted below as H = \, together with a metric, the Poincar├® metric, that makes it a model of two-dimensional hyperbolic geometry.
Equivalently the Poincar├ ...
*Poincar├® disk model
In geometry, the Poincar├® disk model, also called the conformal disk model, is a model of 2-dimensional hyperbolic geometry in which all points are inside the unit disk, and straight lines are either circular arcs contained within the disk ...
* Poincar├® metric
*Inversive geometry
Inversive activities are processes which self internalise the action concerned. For example, a person who has an Inversive personality internalises his emotion
Emotions are mental states brought on by neurophysiological changes, variou ...
Notes
References
*Luis Santal├│ (1961), '' Geometrias no Euclidianas, EUDEBA. * * {{DEFAULTSORT:Beltrami-Klein model Hyperbolic geometry