Aristarchus of Samos

Aristarchus of Samos (; grc-gre, Ἀρίσταρχος ὁ Σάμιος, ''Aristarkhos ho Samios''; ) was an ancient Greek astronomer and mathematician who presented the first known heliocentric model that placed the Sun at the center of the known universe, with the Earth revolving around the Sun once a year and rotating about its axis once a day.

He was a student of Strato of Lampsacus, who was the third head of the Peripatetic School in Greece. According to Ptolemy, during Aristarchus' time there, he observed the summer solstice of 280 BCE. Along with his contributions to the heliocentric model, as reported by Vitruvius, he created two separate sundials: one that is a flat disc; and one hemispherical.

Aristarchus was influenced by the concept presented by Philolaus of Croton (c. 470 – 385 BCE) of a fire at the center of the universe, but Aristarchus identified the "central fire" with the Sun and he put the other planets in their correct order of distance around the Sun.

Like Anaxagoras before him, Aristarchus suspected that the stars were just other bodies like the Sun, albeit farther away from Earth. His astronomical ideas were often rejected in favor of the geocentric theories of Aristotle and Ptolemy. Nicolaus Copernicus knew about the possibility that Aristarchus had a 'moving Earth' theory, although it is unlikely that Copernicus was aware that it was a heliocentric theory.For a (less recent) contrary view that Copernicus did know about Aristarchus's heliocentric theory see: The Philolaus-Aristarchus passage is then given in untranslated Latin, without further comment. This is then followed by quoting in full Archimedes's passage about Aristarchus's heliocentric theory from 'The Sand Reckoner' (using its alternative title ''Arenarius'')', seemingly without mentioning that ''The Sand Reckoner'' was not in print until a year after Copernicus's death (unless this is mentioned in a passage not currently shown by Google Books.).

Aristarchus estimated the sizes of the Sun and Moon as compared to Earth's size. He also estimated the distances from the Earth to the Sun and Moon. He is considered one of the greatest astronomers of antiquity along with Hipparchus, and one of the greatest thinkers in human history.

Heliocentrism

The original text has been lost, but a reference in a book by Archimedes, entitled ''The Sand Reckoner'' (''Archimedis Syracusani Arenarius & Dimensio Circuli''), describes a work in which Aristarchus advanced the heliocentric model as an alternative hypothesis to geocentrism:

Aristarchus suspected the stars were other suns that are very far away, and that in consequence there was no observable parallax, that is, a movement of the stars relative to each other as the Earth moves around the Sun. Since stellar parallax is only detectable with telescopes, his accurate speculation was unprovable at the time.

It is a common misconception that the heliocentric view was held as sacrilegious by the contemporaries of Aristarchus. Lucio Russo traces this to Gilles Ménage's printing of a passage from Plutarch's ''On the Apparent Face in the Orb of the Moon'', in which Aristarchus jokes with Cleanthes, who is head of the Stoics, a sun worshipper, and opposed to heliocentrism.; In the manuscript of Plutarch's text, Aristarchus says Cleanthes should be charged with impiety. Ménage's version, published shortly after the trials of Galileo and Giordano Bruno, transposes an accusative and nominative so that it is Aristarchus who is purported to be impious. The resulting misconception of an isolated and persecuted Aristarchus is still transmitted today.

According to Plutarch, while Aristarchus postulated heliocentrism only as a hypothesis, Seleucus of Seleucia, a Hellenistic astronomer who lived a century after Aristarchus, maintained it as a definite opinion and gave a demonstration of it, but no full record of the demonstration has been found. In his ''Naturalis Historia'', Pliny the Elder later wondered whether errors in the predictions about the heavens could be attributed to a displacement of the Earth from its central position. Pliny and Seneca referred to the retrograde motion of some planets as an apparent (and not real) phenomenon, which is an implication of heliocentrism rather than geocentrism. Still, no stellar parallax was observed, and Plato, Aristotle, and Ptolemy preferred the geocentric model that was held as true throughout the Middle Ages.

The heliocentric theory was revived by Copernicus, after which Johannes Kepler described planetary motions with greater accuracy with his three laws. Isaac Newton later gave a theoretical explanation based on laws of gravitational attraction and dynamics.

After realizing that the Sun was much larger than the Earth and the other planets, Aristarchus concluded that planets revolved around the Sun.

Distance to the Sun

The only known surviving work usually attributed to Aristarchus, '' On the Sizes and Distances of the Sun and Moon'', is based on a geocentric world view. Historically, it has been read as stating that the angle subtended by the Sun's diameter is two degrees, but Archimedes states in ''The Sand Reckoner'' that Aristarchus had a value of half a degree, which is much closer to the average value of 32' or 0.53 degrees. The discrepancy may come from a misinterpretation of what unit of measure was meant by a certain Greek term in the text of Aristarchus.

Aristarchus claimed that at half moon ( first or last quarter moon), the angle between the Sun and Moon was 87°. He might have proposed 87° as a lower bound, since gauging the lunar terminator's deviation from linearity to one degree of accuracy is beyond the unaided human ocular limit (with that limit being about three arcminutes of accuracy). Aristarchus is known to have studied light and vision as well.

Using correct geometry, but the insufficiently accurate 87° datum, Aristarchus concluded that the Sun was between 18 and 20 times farther away from the Earth than the Moon. (The true value of this angle is close to 89° 50', and the Sun's distance is approximately 400 times that of the Moon.) The implicit false solar parallax of slightly under three degrees was used by astronomers up to and including Tycho Brahe, c. AD 1600. Aristarchus pointed out that the Moon and Sun have nearly equal apparent angular sizes, and therefore their diameters must be in proportion to their distances from Earth.

Size of the Moon and Sun

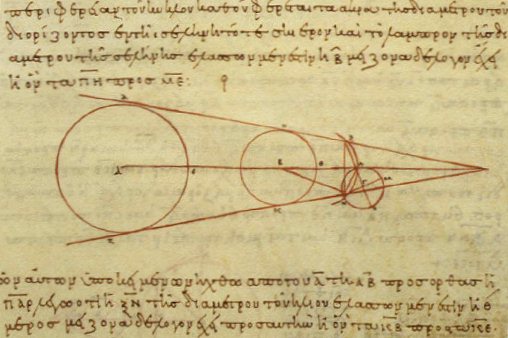
In ''On the Sizes and Distances of the Sun and Moon'', Aristarchus discusses the size of the Moon and Sun in relation to the Earth. In order to achieve these measurements and subsequent calculations, he used several key notes made while observing a lunar eclipse. The first of these consisted of the time that it took for the Earth's shadow to fully encompass the Moon, along with how long the Moon remained within the shadow. This was used to estimate the angular radius of the shadow. From there, using the width of the cone that was created by the shadow in relation to the Moon, he determined that it was twice the diameter of the Moon at the full, non-central eclipse. In addition to this, Aristarchus estimated that the length of the shadow extended around 2.4 times the distance of the Moon from the Earth.

Using these calculations, along with the aforementioned estimated distances of the Sun from the Earth and Moon from the Earth, he created a triangle. Employing a similar method of geometry that he previously used for the distances, he was able to determine that the diameter of the Moon is roughly one-third that of the Earth's diameter. In order to estimate the size of the Sun, Aristarchus considered the proportion of the Sun's distance to Earth in comparison to the Moon's distance from Earth, which was found to be roughly 18 to 20 times the length. Therefore, the size of the Sun is around 19 times wider than the Moon, making it approximately six times wider than the Earth's diameter.

Legacy

The lunar crater Aristarchus, the minor planet 3999 Aristarchus, and the telescope Aristarchos are named after him.

See also

* Aristarchus's inequality
* Eratosthenes (), a Greek mathematician who calculated the circumference of the Earth and also the distance from the Earth to the Sun.
* Hipparchus (), a Greek mathematician who measured the radii of the Sun and the Moon as well as their distances from the Earth.
* Posidonius (), a Greek astronomer and mathematician who calculated the circumference of the Earth.

References

Bibliography

*
*

Further reading

*

External links

Biography: JRASC, 75 (1981) 29


an

from educational websit

* Aristarchus of Samos, The Ancient Copernicus (https://archive.org/details/aristarchusofsam00heatuoft
*
Online Galleries, History of Science Collections, University of Oklahoma Libraries
High resolution images of works by Aristarchus of Samos in .jpg and .tiff format.

{{DEFAULTSORT:Aristarchus Of Samos
310s BC births
230s BC deaths
3rd-century BC Greek people
3rd-century BC writers
Ancient Greek astronomers
Ancient Greek mathematicians
Ancient Samians
3rd-century BC mathematicians