64QAM on:
[Wikipedia]
[Google]
[Amazon]
Quadrature amplitude modulation (QAM) is the name of a family of
 In a QAM signal, one carrier lags the other by 90°, and its amplitude modulation is customarily referred to as the in-phase component, denoted by The other modulating function is the
In a QAM signal, one carrier lags the other by 90°, and its amplitude modulation is customarily referred to as the in-phase component, denoted by The other modulating function is the
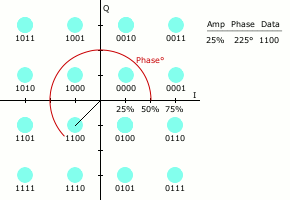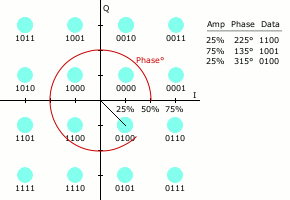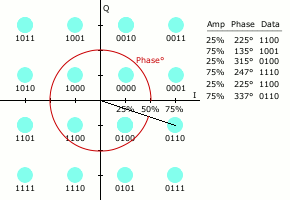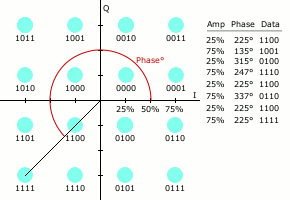
 As in many digital modulation schemes, the
As in many digital modulation schemes, the
ANSI/SCTE 07 2013
Note that many marketing people will refer to these as QAM-64 and QAM-256. In the UK, 64-QAM is used for Communication systems designed to achieve very high levels of
Communication systems designed to achieve very high levels of
QAM Demodulation
Interactive webdemo of QAM constellation with additive noise
Institute of Telecommunicatons, University of Stuttgart
QAM bit error rate for AWGN channel – online experiment
How imperfections affect QAM constellation
Microwave Phase Shifters
Overview by Herley General Microwave
Simulation of dual-polarization QPSK (DP-QPSK) for 100G optical transmission
{{DEFAULTSORT:Quadrature Amplitude Modulation Radio modulation modes Data transmission
digital modulation
In electronics and telecommunications, modulation is the process of varying one or more properties of a periodic waveform, called the ''carrier signal'', with a separate signal called the ''modulation signal'' that typically contains informatio ...
methods and a related family of analog modulation
In electronics and telecommunications, modulation is the process of varying one or more properties of a periodic waveform, called the ''carrier signal'', with a separate signal called the ''modulation signal'' that typically contains informatio ...
methods widely used in modern telecommunications
Telecommunication is the transmission of information by various types of technologies over wire, radio, optical, or other electromagnetic systems. It has its origin in the desire of humans for communication over a distance greater than that fe ...
to transmit information. It conveys two analog message signals, or two digital bit stream
A bitstream (or bit stream), also known as binary sequence, is a sequence of bits.
A bytestream is a sequence of bytes. Typically, each byte is an 8-bit quantity, and so the term octet stream is sometimes used interchangeably. An octet may ...
s, by changing (''modulating'') the amplitude
The amplitude of a periodic variable is a measure of its change in a single period (such as time or spatial period). The amplitude of a non-periodic signal is its magnitude compared with a reference value. There are various definitions of amplit ...
s of two carrier wave
In telecommunications, a carrier wave, carrier signal, or just carrier, is a waveform (usually sinusoidal) that is modulated (modified) with an information-bearing signal for the purpose of conveying information. This carrier wave usually has a ...
s, using the amplitude-shift keying
Amplitude-shift keying (ASK) is a form of amplitude modulation that represents digital data as variations in the amplitude of a carrier wave.
In an ASK system, a symbol, representing one or more bits, is sent by transmitting a fixed-amplitude car ...
(ASK) digital modulation scheme or amplitude modulation
Amplitude modulation (AM) is a modulation technique used in electronic communication, most commonly for transmitting messages with a radio wave. In amplitude modulation, the amplitude (signal strength) of the wave is varied in proportion to ...
(AM) analog modulation scheme. The two carrier waves are of the same frequency and are out of phase
In physics and mathematics, the phase of a periodic function F of some real variable t (such as time) is an angle-like quantity representing the fraction of the cycle covered up to t. It is denoted \phi(t) and expressed in such a scale that it ...
with each other by 90°, a condition known as orthogonality
In mathematics, orthogonality is the generalization of the geometric notion of ''perpendicularity''.
By extension, orthogonality is also used to refer to the separation of specific features of a system. The term also has specialized meanings in ...
or quadrature. The transmitted signal is created by adding the two carrier waves together. At the receiver, the two waves can be coherently separated (demodulated) because of their orthogonality property. Another key property is that the modulations are low-frequency/low-bandwidth waveforms compared to the carrier frequency, which is known as the narrowband assumption.
Phase modulation
Phase modulation (PM) is a modulation pattern for conditioning communication signals for transmission. It encodes a message signal as variations in the instantaneous phase of a carrier wave. Phase modulation is one of the two principal forms ...
(analog PM) and phase-shift keying
Phase-shift keying (PSK) is a digital modulation process which conveys data by changing (modulating) the phase of a constant frequency reference signal (the carrier wave). The modulation is accomplished by varying the sine and cosine inputs at a ...
(digital PSK) can be regarded as a special case of QAM, where the amplitude of the transmitted signal is a constant, but its phase varies. This can also be extended to frequency modulation
Frequency modulation (FM) is the encoding of information in a carrier wave by varying the instantaneous frequency of the wave. The technology is used in telecommunications, radio broadcasting, signal processing, and Run-length limited#FM: .280. ...
(FM) and frequency-shift keying
Frequency-shift keying (FSK) is a frequency modulation scheme in which digital information is transmitted through discrete frequency changes of a carrier signal. The technology is used for communication systems such as telemetry, weather ball ...
(FSK), for these can be regarded as a special case of phase modulation.
QAM is used extensively as a modulation scheme for digital telecommunication
Telecommunication is the transmission of information by various types of technologies over wire, radio, optical, or other electromagnetic systems. It has its origin in the desire of humans for communication over a distance greater than that fe ...
systems, such as in 802.11
IEEE 802.11 is part of the IEEE 802 set of local area network (LAN) technical standards, and specifies the set of media access control (MAC) and physical layer (PHY) protocols for implementing wireless local area network (WLAN) computer com ...
Wi-Fi standards. Arbitrarily high spectral efficiencies can be achieved with QAM by setting a suitable constellation
A constellation is an area on the celestial sphere in which a group of visible stars forms Asterism (astronomy), a perceived pattern or outline, typically representing an animal, mythological subject, or inanimate object.
The origins of the e ...
size, limited only by the noise level and linearity of the communications channel. QAM is being used in optical fiber systems as bit rates increase; QAM16 and QAM64 can be optically emulated with a 3-path interferometer
Interferometry is a technique which uses the ''interference'' of superimposed waves to extract information. Interferometry typically uses electromagnetic waves and is an important investigative technique in the fields of astronomy, fiber op ...
.
Demodulation of QAM
quadrature component
In electrical engineering, a sinusoid with angle modulation can be decomposed into, or synthesized from, two amplitude-modulated sinusoids that are offset in phase by one-quarter cycle (90 degrees or /2 radians). All three functions have the s ...
, So the composite waveform is mathematically modeled as:
: or:
where is the carrier frequency. At the receiver, a coherent demodulator multiplies the received signal separately with both a cosine and sine
In mathematics, sine and cosine are trigonometric functions of an angle. The sine and cosine of an acute angle are defined in the context of a right triangle: for the specified angle, its sine is the ratio of the length of the side that is oppo ...
signal to produce the received estimates of and . For example:
:
Using standard trigonometric identities
In trigonometry, trigonometric identities are equalities that involve trigonometric functions and are true for every value of the occurring variables for which both sides of the equality are defined. Geometrically, these are identities involvin ...
, we can write this as:
:
Low-pass filter
A low-pass filter is a filter that passes signals with a frequency lower than a selected cutoff frequency and attenuates signals with frequencies higher than the cutoff frequency. The exact frequency response of the filter depends on the filter des ...
ing removes the high frequency terms (containing ), leaving only the term. This filtered signal is unaffected by showing that the in-phase component can be received independently of the quadrature component. Similarly, we can multiply by a sine wave and then low-pass filter to extract
The addition of two sinusoids is a linear operation that creates no new frequency components. So the bandwidth of the composite signal is comparable to the bandwidth of the DSB (Double-Sideband) components. Effectively, the spectral redundancy of DSB enables a doubling of the information capacity using this technique. This comes at the expense of demodulation complexity. In particular, a DSB signal has zero-crossings at a regular frequency, which makes it easy to recover the phase of the carrier sinusoid. It is said to be self-clocking. But the sender and receiver of a quadrature-modulated signal must share a clock or otherwise send a clock signal. If the clock phases drift apart, the demodulated ''I'' and ''Q'' signals bleed into each other, yielding crosstalk
In electronics, crosstalk is any phenomenon by which a signal transmitted on one circuit or channel of a transmission system creates an undesired effect in another circuit or channel. Crosstalk is usually caused by undesired capacitive, induc ...
. In this context, the clock signal is called a "phase reference". Clock synchronization is typically achieved by transmitting a burst subcarrier
A subcarrier is a sideband of a radio frequency carrier wave, which is modulated to send additional information. Examples include the provision of colour in a black and white television system or the provision of stereo in a monophonic radio broa ...
or a pilot signal
In telecommunications, a pilot signal is a signal, usually a single frequency, transmitted over a communications system for supervisory, control, equalization, continuity, synchronization, or reference purposes.
Uses in different communication ...
. The phase reference for NTSC
The first American standard for analog television broadcast was developed by National Television System Committee (NTSC)National Television System Committee (1951–1953), Report and Reports of Panel No. 11, 11-A, 12–19, with Some supplement ...
, for example, is included within its colorburst
Colorburst is an analog video, composite video signal generated by a video-signal generator used to keep the chrominance subcarrier synchronized in a color television signal. By synchronizing an oscillator with the colorburst at the back porc ...
signal.
Analog QAM is used in:
* NTSC
The first American standard for analog television broadcast was developed by National Television System Committee (NTSC)National Television System Committee (1951–1953), Report and Reports of Panel No. 11, 11-A, 12–19, with Some supplement ...
and PAL
Phase Alternating Line (PAL) is a colour encoding system for analogue television. It was one of three major analogue colour television standards, the others being NTSC and SECAM. In most countries it was broadcast at 625 lines, 50 fields (25 ...
analog color television
Color television or Colour television is a television transmission technology that includes color information for the picture, so the video image can be displayed in color on the television set. It improves on the monochrome or black-and-white t ...
systems, where the I- and Q-signals carry the components of chroma (colour) information. The QAM carrier phase is recovered from a special colorburst transmitted at the beginning of each scan line.
* C-QUAM
C-QUAM (Compatible QUadrature Amplitude Modulation) is the method of AM stereo broadcasting used in Canada, the United States and most other countries. It was invented in 1977 by Norman Parker, Francis Hilbert, and Yoshio Sakaie, and published i ...
("Compatible QAM") is used in AM stereo radio to carry the stereo difference information.
Fourier analysis of QAM
In thefrequency domain
In physics, electronics, control systems engineering, and statistics, the frequency domain refers to the analysis of mathematical functions or signals with respect to frequency, rather than time. Put simply, a time-domain graph shows how a signa ...
, QAM has a similar spectral pattern to DSB-SC modulation. Applying Euler's formula
Euler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the fundamental relationship between the trigonometric functions and the complex exponential function. Euler's formula states that for an ...
to the sinusoids in , the positive-frequency portion of (or analytic representation) is:
:
where denotes the Fourier transform, and and are the transforms of and This result represents the sum of two DSB-SC signals with the same center frequency. The factor of represents the 90° phase shift that enables their individual demodulations.
Digital QAM

constellation diagram
A constellation diagram is a representation of a signal modulated by a digital modulation scheme such as quadrature amplitude modulation or phase-shift keying. It displays the signal as a two-dimensional ''xy''-plane scatter diagram in the ...
is useful for QAM. In QAM, the constellation points are usually arranged in a square grid with equal vertical and horizontal spacing, although other configurations are possible (e.g. a hexagonal or triangular grid). In digital telecommunications
Telecommunication is the transmission of information by various types of technologies over wire, radio, optical, or other electromagnetic systems. It has its origin in the desire of humans for communication over a distance greater than that fe ...
the data is usually binary
Binary may refer to:
Science and technology Mathematics
* Binary number, a representation of numbers using only two digits (0 and 1)
* Binary function, a function that takes two arguments
* Binary operation, a mathematical operation that t ...
, so the number of points in the grid is typically a power of 2 (2, 4, 8, …), corresponding to the number of bits per symbol. The simplest and most commonly used QAM constellations consist of points arranged in a square, i.e. 16-QAM, 64-QAM and 256-QAM (even powers of two). Non-square constellations, such as Cross-QAM, can offer greater efficiency but are rarely used because of the cost of increased modem complexity.
By moving to a higher-order constellation, it is possible to transmit more bit
The bit is the most basic unit of information in computing and digital communications. The name is a portmanteau of binary digit. The bit represents a logical state with one of two possible values. These values are most commonly represente ...
s per symbol
A symbol is a mark, sign, or word that indicates, signifies, or is understood as representing an idea, object, or relationship. Symbols allow people to go beyond what is known or seen by creating linkages between otherwise very different conc ...
. However, if the mean energy of the constellation is to remain the same (by way of making a fair comparison), the points must be closer together and are thus more susceptible to noise
Noise is unwanted sound considered unpleasant, loud or disruptive to hearing. From a physics standpoint, there is no distinction between noise and desired sound, as both are vibrations through a medium, such as air or water. The difference arise ...
and other corruption; this results in a higher bit error rate
In digital transmission, the number of bit errors is the number of received bits of a data stream over a communication channel that have been altered due to noise, interference, distortion or bit synchronization errors.
The bit error rate (BER) i ...
and so higher-order QAM can deliver more data less reliably than lower-order QAM, for constant mean constellation energy. Using higher-order QAM without increasing the bit error rate requires a higher signal-to-noise ratio
Signal-to-noise ratio (SNR or S/N) is a measure used in science and engineering that compares the level of a desired signal to the level of background noise. SNR is defined as the ratio of signal power to the noise power, often expressed in deci ...
(SNR) by increasing signal energy, reducing noise, or both.
If data-rates beyond those offered by 8- PSK are required, it is more usual to move to QAM since it achieves a greater distance between adjacent points in the I-Q plane by distributing the points more evenly. The complicating factor is that the points are no longer all the same amplitude and so the demodulator
Demodulation is extracting the original information-bearing signal from a carrier wave. A demodulator is an electronic circuit (or computer program in a software-defined radio) that is used to recover the information content from the modulated ...
must now correctly detect both phase
Phase or phases may refer to:
Science
*State of matter, or phase, one of the distinct forms in which matter can exist
*Phase (matter), a region of space throughout which all physical properties are essentially uniform
* Phase space, a mathematic ...
and amplitude
The amplitude of a periodic variable is a measure of its change in a single period (such as time or spatial period). The amplitude of a non-periodic signal is its magnitude compared with a reference value. There are various definitions of amplit ...
, rather than just phase.
64-QAM and 256-QAM are often used in digital cable
Digital cable is the distribution of cable television using digital data and video compression. The technology was first developed by General Instrument. By 2000, most cable companies offered digital features, eventually replacing their previou ...
television and cable modem
A cable modem is a type of network bridge that provides bi-directional data communication via radio frequency channels on a hybrid fibre-coaxial (HFC), radio frequency over glass (RFoG) and coaxial cable infrastructure. Cable modems are primaril ...
applications. In the United States, 64-QAM and 256-QAM are the mandated modulation schemes for digital cable
Digital cable is the distribution of cable television using digital data and video compression. The technology was first developed by General Instrument. By 2000, most cable companies offered digital features, eventually replacing their previou ...
(see QAM tuner
QAM is a digital television standard using quadrature amplitude modulation. It is the format by which digital cable channels are encoded and transmitted via cable television providers. QAM is used in a variety of communications systems such as Di ...
) as standardised by the SCTE in the standarANSI/SCTE 07 2013
Note that many marketing people will refer to these as QAM-64 and QAM-256. In the UK, 64-QAM is used for
digital terrestrial television
Digital terrestrial television (DTTV or DTT, or DTTB with "broadcasting") is a technology for terrestrial television in which land-based (terrestrial) television stations broadcast television content by radio waves to televisions in consumers' ...
(Freeview Freeview may refer to:
* Freeview (Australia), the marketing name for the digital terrestrial television platform in Australia
* Freeview (New Zealand), a digital satellite and digital terrestrial television platform in New Zealand
*Freeview (UK), ...
) whilst 256-QAM is used for Freeview-HD.
 Communication systems designed to achieve very high levels of
Communication systems designed to achieve very high levels of spectral efficiency
Spectral efficiency, spectrum efficiency or bandwidth efficiency refers to the information rate that can be transmitted over a given bandwidth in a specific communication system. It is a measure of how efficiently a limited frequency spectrum is ut ...
usually employ very dense QAM constellations. For example, current Homeplug AV2 500-Mbit/s powerline Ethernet
Power-line communication (also known as power-line carrier or PLC) carries data on a conductor that is also used simultaneously for AC electric power transmission or electric power distribution to consumers.
A wide range of power-line communicati ...
devices use 1024-QAM and 4096-QAM, as well as future devices using ITU-T
The ITU Telecommunication Standardization Sector (ITU-T) is one of the three sectors (divisions or units) of the International Telecommunication Union (ITU). It is responsible for coordinating standards for telecommunications and Information Commu ...
G.hn
G.hn is a specification for home networking with data rates up to 2 Gbit/s and operation over four types of legacy wires: telephone wiring, coaxial cables, power lines and plastic optical fiber. A single G.hn semiconductor device is able to n ...
standard for networking over existing home wiring (coaxial cable
Coaxial cable, or coax (pronounced ) is a type of electrical cable consisting of an inner conductor surrounded by a concentric conducting shield, with the two separated by a dielectric ( insulating material); many coaxial cables also have a p ...
, phone line
A telephone line or telephone circuit (or just line or circuit industrywide) is a single-user circuit on a telephone communication system. It is designed to reproduce speech of a quality that is understandable. It is the physical wire or ot ...
s and power lines
Electric power transmission is the bulk movement of electrical energy from a generating site, such as a power plant, to an electrical substation. The interconnected lines that facilitate this movement form a ''transmission network''. This is d ...
); 4096-QAM provides 12 bits/symbol. Another example is ADSL
Asymmetric digital subscriber line (ADSL) is a type of digital subscriber line (DSL) technology, a data communications technology that enables faster data transmission over copper telephone lines than a conventional voiceband modem can provide. ...
technology for copper twisted pairs, whose constellation size goes up to 32768-QAM (in ADSL terminology this is referred to as bit-loading, or bit per tone, 32768-QAM being equivalent to 15 bits per tone).
Ultra-high capacity Microwave Backhaul Systems also use 1024-QAM.http://www.trangosys.com/products/point-to-point-wireless-backhaul/licensed-wireless/trangolink-apex-orion.shtml A Apex Orion With 1024-QAM, adaptive coding and modulation Link adaptation, comprising adaptive coding and modulation (ACM) and others (such as Power Control), is a term used in wireless communications to denote the matching of the modulation, coding and other signal and protocol parameters to the conditi ...
(ACM) and XPIC XPIC, or cross-polarization interference cancelling technology, is an algorithm to suppress mutual interference between two received streams in a Polarization-division multiplexing communication system.
The cross-polarization interference cancelle ...
, vendors can obtain gigabit capacity in a single 56 MHz channel.
Interference and noise
In moving to a higher order QAM constellation (higher data rate and mode) in hostile RF/microwave
Microwave is a form of electromagnetic radiation with wavelengths ranging from about one meter to one millimeter corresponding to frequencies between 300 MHz and 300 GHz respectively. Different sources define different frequency ran ...
QAM application environments, such as in broadcasting
Broadcasting is the distribution (business), distribution of sound, audio or video content to a dispersed audience via any electronic medium (communication), mass communications medium, but typically one using the electromagnetic spectrum (radio ...
or telecommunications
Telecommunication is the transmission of information by various types of technologies over wire, radio, optical, or other electromagnetic systems. It has its origin in the desire of humans for communication over a distance greater than that fe ...
, multipath interference
In radio communication, multipath is the propagation phenomenon that results in radio signals reaching the receiving antenna by two or more paths. Causes of multipath include atmospheric ducting, ionospheric reflection and refraction, and refle ...
typically increases. There is a spreading of the spots in the constellation, decreasing the separation between adjacent states, making it difficult for the receiver to decode the signal appropriately. In other words, there is reduced noise
Noise is unwanted sound considered unpleasant, loud or disruptive to hearing. From a physics standpoint, there is no distinction between noise and desired sound, as both are vibrations through a medium, such as air or water. The difference arise ...
immunity. There are several test parameter measurements which help determine an optimal QAM mode for a specific operating environment. The following three are most significant:
* Carrier/interference ratio
* Carrier-to-noise ratio
* Threshold-to-noise ratio
See also
* Amplitude and phase-shift keying or asymmetric phase-shift keying (APSK) * Carrierless amplitude phase modulation (CAP) * *In-phase and quadrature components
In electrical engineering, a sinusoid with angle modulation can be decomposed into, or synthesized from, two amplitude-modulated sinusoids that are offset in phase by one-quarter cycle (90 degrees or /2 radians). All three functions have the s ...
* Modulation
In electronics and telecommunications, modulation is the process of varying one or more properties of a periodic waveform, called the ''carrier signal'', with a separate signal called the ''modulation signal'' that typically contains informatio ...
for other examples of modulation techniques
* Phase-shift keying
Phase-shift keying (PSK) is a digital modulation process which conveys data by changing (modulating) the phase of a constant frequency reference signal (the carrier wave). The modulation is accomplished by varying the sine and cosine inputs at a ...
* QAM tuner
QAM is a digital television standard using quadrature amplitude modulation. It is the format by which digital cable channels are encoded and transmitted via cable television providers. QAM is used in a variety of communications systems such as Di ...
for HDTV
* Random modulation In the theories of modulation and of stochastic processes, random modulation is the creation of a new signal from two other signals by the process of quadrature amplitude modulation. In particular, the two signals are considered as being random proc ...
References
Further reading
*Jonqyin (Russell) Sun "Linear diversity analysis for QAM in Rician fading channels", IEEE WOCC 2014 *''John G. Proakis'', "''Digital Communications, 3rd Edition''"External links
QAM Demodulation
Interactive webdemo of QAM constellation with additive noise
Institute of Telecommunicatons, University of Stuttgart
QAM bit error rate for AWGN channel – online experiment
How imperfections affect QAM constellation
Microwave Phase Shifters
Overview by Herley General Microwave
Simulation of dual-polarization QPSK (DP-QPSK) for 100G optical transmission
{{DEFAULTSORT:Quadrature Amplitude Modulation Radio modulation modes Data transmission