|
Time Constant
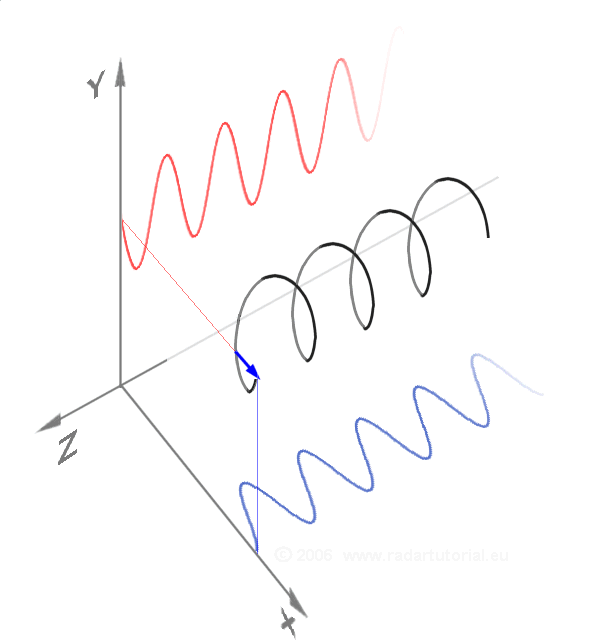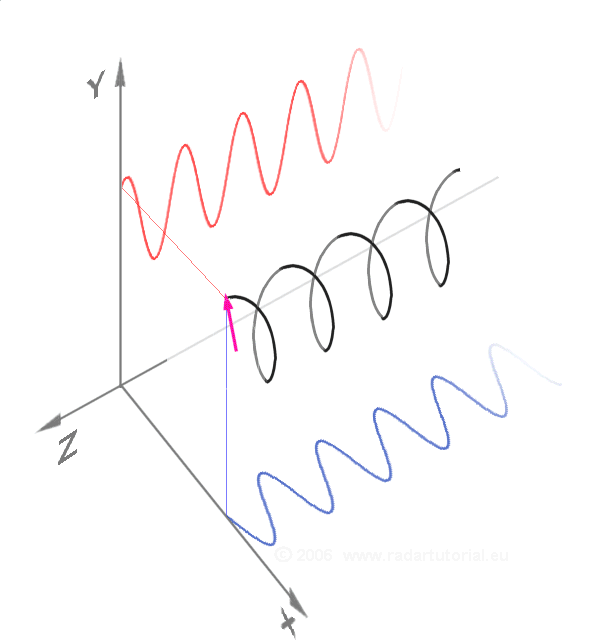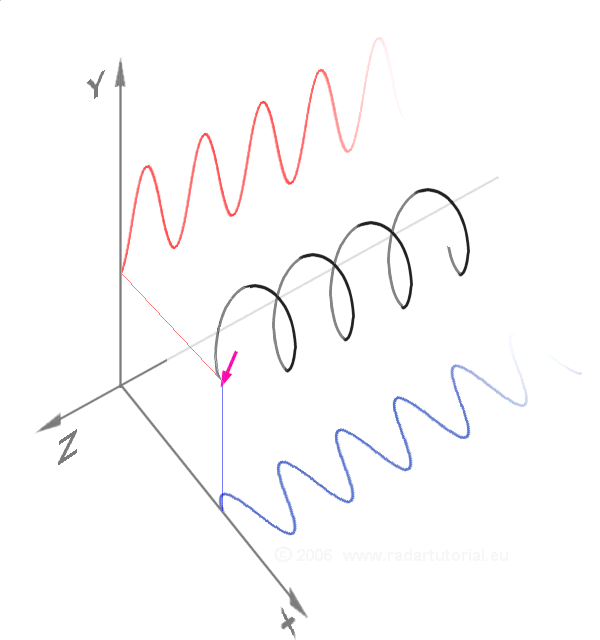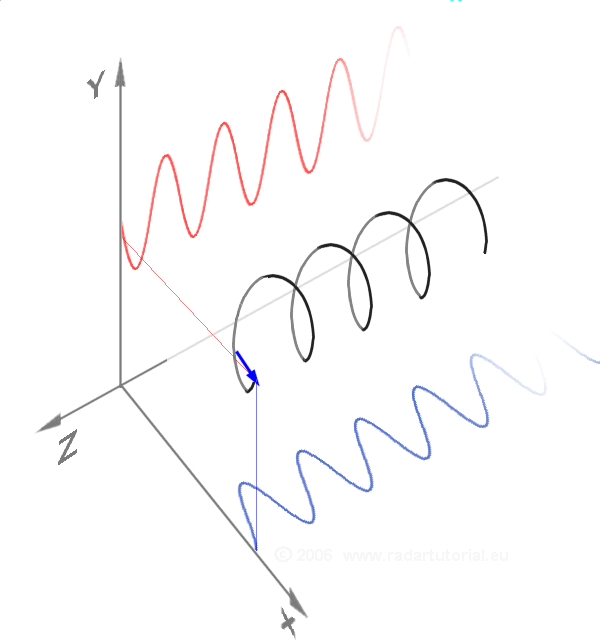
In physics and engineering, the time constant, usually denoted by the Greek language, Greek letter (tau), is the parameter characterizing the response to a step input of a first-order, LTI system theory, linear time-invariant (LTI) system.Concretely, a first-order LTI system is a system that can be modeled by a single Ordinary differential equation, first order differential equation in time. Examples include the simplest single-stage electrical RC circuit#Series circuit, RC circuits and RL circuit#Series circuit, RL circuits. The time constant is the main characteristic unit of a first-order LTI system. It gives speed of the response. In the time domain, the usual choice to explore the time response is through the step response to a Heaviside step function, step input, or the impulse response to a Dirac delta function input. In the frequency domain (for example, looking at the Fourier transform of the step response, or using an input that is a simple sinusoidal function of time) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Physics
Physics is the scientific study of matter, its Elementary particle, fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge which relates to the order of nature, or, in other words, to the regular succession of events." It is one of the most fundamental scientific disciplines. "Physics is one of the most fundamental of the sciences. Scientists of all disciplines use the ideas of physics, including chemists who study the structure of molecules, paleontologists who try to reconstruct how dinosaurs walked, and climatologists who study how human activities affect the atmosphere and oceans. Physics is also the foundation of all engineering and technology. No engineer could design a flat-screen TV, an interplanetary spacecraft, or even a better mousetrap without first understanding the basic laws of physics. (...) You will come to see physics as a towering achievement of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Radio Transmitter
In electronics and telecommunications, a radio transmitter or just transmitter (often abbreviated as XMTR or TX in technical documents) is an electronic device which produces radio waves with an antenna with the purpose of signal transmission to a radio receiver. The transmitter itself generates a radio frequency alternating current, which is applied to the antenna. When excited by this alternating current, the antenna radiates radio waves. Transmitters are necessary component parts of all electronic devices that communicate by radio, such as radio (audio) and television broadcasting stations, cell phones, walkie-talkies, wireless computer networks, Bluetooth enabled devices, garage door openers, two-way radios in aircraft, ships, spacecraft, radar sets and navigational beacons. The term ''transmitter'' is usually limited to equipment that generates radio waves for communication purposes; or radiolocation, such as radar and navigational transmitters. Generators of radio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Decibels
The decibel (symbol: dB) is a relative unit of measurement equal to one tenth of a bel (B). It expresses the ratio of two values of a power or root-power quantity on a logarithmic scale. Two signals whose levels differ by one decibel have a power ratio of 101/10 (approximately ) or root-power ratio of 101/20 (approximately ). The strict original usage above only expresses a relative change. However, the word decibel has since also been used for expressing an absolute value that is relative to some fixed reference value, in which case the dB symbol is often suffixed with letter codes that indicate the reference value. For example, for the reference value of 1 volt, a common suffix is " V" (e.g., "20 dBV"). As it originated from a need to express power ratios, two principal types of scaling of the decibel are used to provide consistency depending on whether the scaling refers to ratios of power quantities or root-power quantities. When expressing a power ratio, it ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Steady-state
In systems theory, a system or a process is in a steady state if the variables (called state variables) which define the behavior of the system or the process are unchanging in time. In continuous time, this means that for those properties ''p'' of the system, the partial derivative with respect to time is zero and remains so: : \frac = 0 \quad \text t. In discrete time, it means that the first difference of each property is zero and remains so: : p_t-p_=0 \quad \text t. The concept of a steady state has relevance in many fields, in particular thermodynamics, economics, and engineering. If a system is in a steady state, then the recently observed behavior of the system will continue into the future. In stochastic systems, the probabilities that various states will be repeated will remain constant. For example, see ' for the derivation of the steady state. In many systems, a steady state is not achieved until some time after the system is started or initiated. This initial situ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Euler's Formula
Euler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the fundamental relationship between the trigonometric functions and the complex exponential function. Euler's formula states that, for any real number , one has e^ = \cos x + i \sin x, where is the base of the natural logarithm, is the imaginary unit, and and are the trigonometric functions cosine and sine respectively. This complex exponential function is sometimes denoted ("cosine plus ''i'' sine"). The formula is still valid if is a complex number, and is also called ''Euler's formula'' in this more general case. Euler's formula is ubiquitous in mathematics, physics, chemistry, and engineering. The physicist Richard Feynman called the equation "our jewel" and "the most remarkable formula in mathematics". When , Euler's formula may be rewritten as or , which is known as Euler's identity. History In 1714, the English mathematician Roger Cotes prese ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Single-pole Frequency Response
In electrical engineering, a switch is an electrical component that can disconnect or connect the conducting path in an electrical circuit, interrupting the electric current or diverting it from one conductor to another. The most common type of switch is an electromechanical device consisting of one or more sets of movable electrical contacts connected to external circuits. When a pair of contacts is touching current can pass between them, while when the contacts are separated no current can flow. Switches are made in many different configurations; they may have multiple sets of contacts controlled by the same knob or actuator, and the contacts may operate simultaneously, sequentially, or alternately. A switch may be operated manually, for example, a light switch or a keyboard button, or may function as a sensing element to sense the position of a machine part, liquid level, pressure, or temperature, such as a thermostat. Many specialized forms exist, such as the toggle switc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Exponential Decay
A quantity is subject to exponential decay if it decreases at a rate proportional to its current value. Symbolically, this process can be expressed by the following differential equation, where is the quantity and (lambda Lambda (; uppercase , lowercase ; , ''lám(b)da'') is the eleventh letter of the Greek alphabet, representing the voiced alveolar lateral approximant . In the system of Greek numerals, lambda has a value of 30. Lambda is derived from the Phoen ...) is a positive rate called the exponential decay constant, disintegration constant, rate constant, or transformation constant: :\frac = -\lambda N(t). The solution to this equation (see #Solution_of_the_differential_equation, derivation below) is: :N(t) = N_0 e^, where is the quantity at time , is the initial quantity, that is, the quantity at time . Measuring rates of decay Mean lifetime If the decaying quantity, ''N''(''t''), is the number of discrete elements in a certain set (mathematics), se ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Half-life
Half-life is a mathematical and scientific description of exponential or gradual decay. Half-life, half life or halflife may also refer to: Film * Half-Life (film), ''Half-Life'' (film), a 2008 independent film by Jennifer Phang * ''Half Life: A Parable for the Nuclear Age'', a 1985 Australian documentary film Literature * Half Life (Jackson novel), ''Half Life'' (Jackson novel), a 2006 novel by Shelley Jackson * Half-Life (Krach novel), ''Half-Life'' (Krach novel), a 2004 novel by Aaron Krach * Halflife (Michalowski novel), ''Halflife'' (Michalowski novel), a 2004 novel by Mark Michalowski * ''Rozpad połowiczny'' (), a 1988 award-winning dystopia novel by Edmund Wnuk-Lipiński Music *Half Life (3 album), ''Half Life'' (3 album) (2001) *Halflife (EP), ''Halflife'' (EP), an EP by Lacuna Coil and the title track *''Half-Life E.P.'', an EP by Local H * "Half Life", a song by 10 Years from ''The Autumn Effect'' * "Half Life", a song by Come from ''Near-Life Experience'' * "Ha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Decay Constant
A quantity is subject to exponential decay if it decreases at a rate proportional to its current value. Symbolically, this process can be expressed by the following differential equation, where is the quantity and (lambda) is a positive rate called the exponential decay constant, disintegration constant, rate constant, or transformation constant: :\frac = -\lambda N(t). The solution to this equation (see derivation below) is: :N(t) = N_0 e^, where is the quantity at time , is the initial quantity, that is, the quantity at time . Measuring rates of decay Mean lifetime If the decaying quantity, ''N''(''t''), is the number of discrete elements in a certain set, it is possible to compute the average length of time that an element remains in the set. This is called the mean lifetime (or simply the lifetime), where the exponential time constant, \tau, relates to the decay rate constant, λ, in the following way: :\tau = \frac. The mean lifetime can be looked at ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Lumped System Analysis
The lumped-element model (also called lumped-parameter model, or lumped-component model) is a idealization (philosophy of science), simplified representation of a physical system or circuit that assumes all components are concentrated at a single point and their behavior can be described by idealized mathematical models. The lumped-element model simplifies the system or circuit behavior description into a Topology (electrical circuits), topology. It is useful in electrical network, electrical systems (including electronics), mechanical multibody systems, heat transfer, acoustics, etc. This is in contrast to distributed parameter systems or models in which the behaviour is distributed spatially and cannot be considered as localized into discrete entities. The simplification reduces the State space (controls), state space of the system to a counting number, finite dimension, and the partial differential equations (PDEs) of the continuous (infinite-dimensional) time and space model ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Pneumatic
Pneumatics (from Greek 'wind, breath') is the use of gas or pressurized air in mechanical systems. Pneumatic systems used in Industrial sector, industry are commonly powered by compressed air or compressed inert gases. A centrally located and electrically-powered Gas compressor, compressor powers Pneumatic cylinder, cylinders, air motors, pneumatic actuators, and other pneumatic devices. A pneumatic system controlled through manual or automatic solenoid valves is selected when it provides a lower cost, more flexible, or safer alternative to electric motors, and hydraulic actuators. Pneumatics also has applications in dentistry, construction, mining, and other areas. History Although the early history of pneumatics is somewhat unclear, blowguns are often considered the earliest pneumatic device, being created independently by various indigenous groups around the world. Bellows are an early form of air compressor used primarily for smelting and forging. Ctesibius of Alexand ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |