|
Idempotent Matrix
In linear algebra, an idempotent matrix is a matrix which, when multiplied by itself, yields itself. That is, the matrix A is idempotent if and only if A^2 = A. For this product A^2 to be defined, A must necessarily be a square matrix. Viewed this way, idempotent matrices are idempotent elements of matrix rings. Example Examples of 2 \times 2 idempotent matrices are: \begin 1 & 0 \\ 0 & 1 \end \qquad \begin 3 & -6 \\ 1 & -2 \end Examples of 3 \times 3 idempotent matrices are: \begin 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end \qquad \begin 2 & -2 & -4 \\ -1 & 3 & 4 \\ 1 & -2 & -3 \end Real 2 × 2 case If a matrix \begina & b \\ c & d \end is idempotent, then * a = a^2 + bc, * b = ab + bd, implying b(1 - a - d) = 0 so b = 0 or d = 1 - a, * c = ca + cd, implying c(1 - a - d) = 0 so c = 0 or d = 1 - a, * d = bc + d^2. Thus, a necessary condition for a 2\times2 matrix to be idempotent is that either it is diagonal or its trace equals 1. For idempotent diagonal matrices, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Linear Algebra
Linear algebra is the branch of mathematics concerning linear equations such as :a_1x_1+\cdots +a_nx_n=b, linear maps such as :(x_1, \ldots, x_n) \mapsto a_1x_1+\cdots +a_nx_n, and their representations in vector spaces and through matrix (mathematics), matrices. Linear algebra is central to almost all areas of mathematics. For instance, linear algebra is fundamental in modern presentations of geometry, including for defining basic objects such as line (geometry), lines, plane (geometry), planes and rotation (mathematics), rotations. Also, functional analysis, a branch of mathematical analysis, may be viewed as the application of linear algebra to Space of functions, function spaces. Linear algebra is also used in most sciences and fields of engineering because it allows mathematical model, modeling many natural phenomena, and computing efficiently with such models. For nonlinear systems, which cannot be modeled with linear algebra, it is often used for dealing with first-order a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Statistics
Statistics (from German language, German: ', "description of a State (polity), state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a scientific, industrial, or social problem, it is conventional to begin with a statistical population or a statistical model to be studied. Populations can be diverse groups of people or objects such as "all people living in a country" or "every atom composing a crystal". Statistics deals with every aspect of data, including the planning of data collection in terms of the design of statistical survey, surveys and experimental design, experiments. When census data (comprising every member of the target population) cannot be collected, statisticians collect data by developing specific experiment designs and survey sample (statistics), samples. Representative sampling assures that inferences and conclusions can reasonably extend from the sample ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Orthogonal Projection
In linear algebra and functional analysis, a projection is a linear transformation P from a vector space to itself (an endomorphism) such that P\circ P=P. That is, whenever P is applied twice to any vector, it gives the same result as if it were applied once (i.e. P is idempotent). It leaves its image unchanged. This definition of "projection" formalizes and generalizes the idea of graphical projection. One can also consider the effect of a projection on a geometrical object by examining the effect of the projection on points in the object. Definitions A projection on a vector space V is a linear operator P\colon V \to V such that P^2 = P. When V has an inner product and is complete, i.e. when V is a Hilbert space, the concept of orthogonality can be used. A projection P on a Hilbert space V is called an orthogonal projection if it satisfies \langle P \mathbf x, \mathbf y \rangle = \langle \mathbf x, P \mathbf y \rangle for all \mathbf x, \mathbf y \in V. A projection on a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Null Space
In mathematics, the kernel of a linear map, also known as the null space or nullspace, is the part of the domain which is mapped to the zero vector of the co-domain; the kernel is always a linear subspace of the domain. That is, given a linear map between two vector spaces and , the kernel of is the vector space of all elements of such that , where denotes the zero vector in , or more symbolically: \ker(L) = \left\ = L^(\mathbf). Properties The kernel of is a linear subspace of the domain .Linear algebra, as discussed in this article, is a very well established mathematical discipline for which there are many sources. Almost all of the material in this article can be found in , , and Strang's lectures. In the linear map L : V \to W, two elements of have the same image in if and only if their difference lies in the kernel of , that is, L\left(\mathbf_1\right) = L\left(\mathbf_2\right) \quad \text \quad L\left(\mathbf_1-\mathbf_2\right) = \mathbf. From this, it follows ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Column Space
In linear algebra, the column space (also called the range or image) of a matrix ''A'' is the span (set of all possible linear combinations) of its column vectors. The column space of a matrix is the image or range of the corresponding matrix transformation. Let F be a field. The column space of an matrix with components from F is a linear subspace of the ''m''-space F^m. The dimension of the column space is called the rank of the matrix and is at most .Linear algebra, as discussed in this article, is a very well established mathematical discipline for which there are many sources. Almost all of the material in this article can be found in Lay 2005, Meyer 2001, and Strang 2005. A definition for matrices over a ring R is also possible. The row space is defined similarly. The row space and the column space of a matrix are sometimes denoted as and respectively. This article considers matrices of real numbers. The row and column spaces are subspaces of the real sp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Hat Matrix
In statistics, the projection matrix (\mathbf), sometimes also called the influence matrix or hat matrix (\mathbf), maps the vector of response values (dependent variable values) to the vector of fitted values (or predicted values). It describes the influence each response value has on each fitted value. The diagonal elements of the projection matrix are the leverages, which describe the influence each response value has on the fitted value for that same observation. Definition If the vector of response values is denoted by \mathbf and the vector of fitted values by \mathbf, :\mathbf = \mathbf \mathbf. As \mathbf is usually pronounced "y-hat", the projection matrix \mathbf is also named ''hat matrix'' as it "puts a hat on \mathbf". Application for residuals The formula for the vector of residuals \mathbf can also be expressed compactly using the projection matrix: :\mathbf = \mathbf - \mathbf = \mathbf - \mathbf \mathbf = \left( \mathbf - \mathbf \right) \mathbf. where \math ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Transpose
In linear algebra, the transpose of a Matrix (mathematics), matrix is an operator which flips a matrix over its diagonal; that is, it switches the row and column indices of the matrix by producing another matrix, often denoted by (among other notations). The transpose of a matrix was introduced in 1858 by the British mathematician Arthur Cayley. Transpose of a matrix Definition The transpose of a matrix , denoted by , , , A^, , , or , may be constructed by any one of the following methods: #Reflection (mathematics), Reflect over its main diagonal (which runs from top-left to bottom-right) to obtain #Write the rows of as the columns of #Write the columns of as the rows of Formally, the -th row, -th column element of is the -th row, -th column element of : :\left[\mathbf^\operatorname\right]_ = \left[\mathbf\right]_. If is an matrix, then is an matrix. In the case of square matrices, may also denote the th power of the matrix . For avoiding a possibl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Dependent And Independent Variables
A variable is considered dependent if it depends on (or is hypothesized to depend on) an independent variable. Dependent variables are studied under the supposition or demand that they depend, by some law or rule (e.g., by a mathematical function), on the values of other variables. Independent variables, on the other hand, are not seen as depending on any other variable in the scope of the experiment in question. Rather, they are controlled by the experimenter. In pure mathematics In mathematics, a function (mathematics), function is a rule for taking an input (in the simplest case, a number or set of numbers)Carlson, Robert. A concrete introduction to real analysis. CRC Press, 2006. p.183 and providing an output (which may also be a number). A symbol that stands for an arbitrary input is called an independent variable, while a symbol that stands for an arbitrary output is called a dependent variable. The most common symbol for the input is , and the most common symbol for the o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
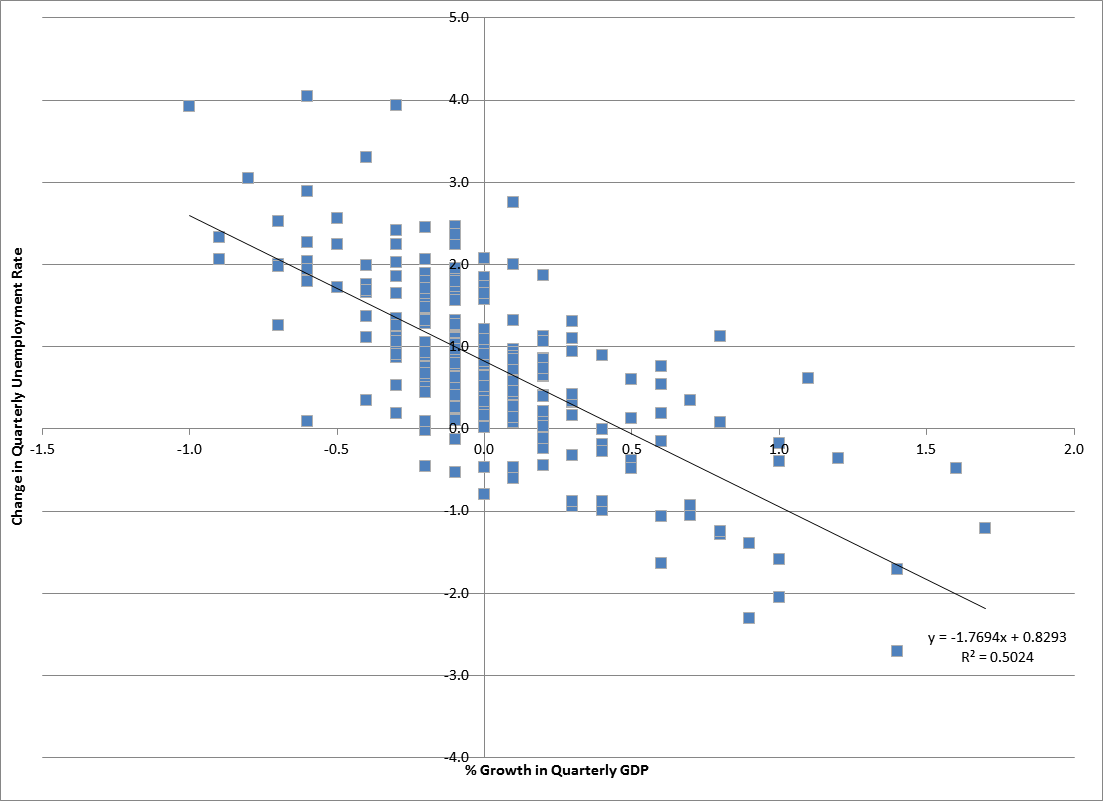
Ordinary Least Squares
In statistics, ordinary least squares (OLS) is a type of linear least squares method for choosing the unknown parameters in a linear regression In statistics, linear regression is a statistical model, model that estimates the relationship between a Scalar (mathematics), scalar response (dependent variable) and one or more explanatory variables (regressor or independent variable). A mode ... model (with fixed level-one effects of a linear function of a set of explanatory variables) by the principle of least squares: minimizing the sum of the squares of the differences between the observed dependent variable (values of the variable being observed) in the input dataset and the output of the (linear) function of the independent variable. Some sources consider OLS to be linear regression. Geometrically, this is seen as the sum of the squared distances, parallel to the axis of the dependent variable, between each data point in the set and the corresponding point on the regression ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Econometrics
Econometrics is an application of statistical methods to economic data in order to give empirical content to economic relationships. M. Hashem Pesaran (1987). "Econometrics", '' The New Palgrave: A Dictionary of Economics'', v. 2, p. 8 p. 8–22 Reprinted in J. Eatwell ''et al.'', eds. (1990). ''Econometrics: The New Palgrave''p. 1 p. 1–34Abstract ( 2008 revision by J. Geweke, J. Horowitz, and H. P. Pesaran). More precisely, it is "the quantitative analysis of actual economic phenomena based on the concurrent development of theory and observation, related by appropriate methods of inference." An introductory economics textbook describes econometrics as allowing economists "to sift through mountains of data to extract simple relationships." Jan Tinbergen is one of the two founding fathers of econometrics. The other, Ragnar Frisch, also coined the term in the sense in which it is used today. A basic tool for econometrics is the multiple linear regression model. ''Econome ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Change Of Basis
In mathematics, an ordered basis of a vector space of finite dimension allows representing uniquely any element of the vector space by a coordinate vector, which is a sequence of scalars called coordinates. If two different bases are considered, the coordinate vector that represents a vector on one basis is, in general, different from the coordinate vector that represents on the other basis. A change of basis consists of converting every assertion expressed in terms of coordinates relative to one basis into an assertion expressed in terms of coordinates relative to the other basis. Such a conversion results from the ''change-of-basis formula'' which expresses the coordinates relative to one basis in terms of coordinates relative to the other basis. Using matrices, this formula can be written :\mathbf x_\mathrm = A \,\mathbf x_\mathrm, where "old" and "new" refer respectively to the initially defined basis and the other basis, \mathbf x_\mathrm and \mathbf x_\mathrm are the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |