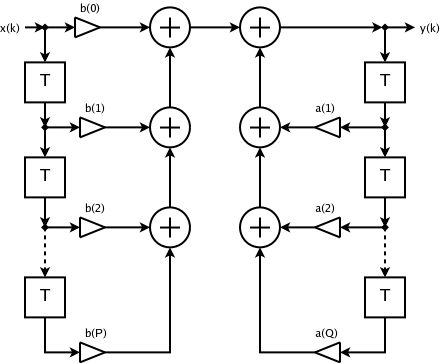
|
Digital Delay
A digital delay line (or simply delay line, also called delay filter) is a discrete element in a digital filter, which allows a signal to be delayed by a number of samples. Delay lines are commonly used to delay audio signals feeding loudspeakers to compensate for the speed of sound in air, and to align video signals with accompanying audio, called audio-to-video synchronization. Delay lines may compensate for electronic processing latency so that multiple signals leave a device simultaneously despite having different pathways. Digital delay lines are widely used building blocks in methods to simulate room acoustics, musical instruments and effects units. Digital waveguide synthesis shows how digital delay lines can be used as sound synthesis methods for various musical instruments such as string instruments and wind instruments. If a delay line holds a non-integer value smaller than one, it results in a fractional delay line (also called interpolated delay line or fraction ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Digital Signal Processing
Digital signal processing (DSP) is the use of digital processing, such as by computers or more specialized digital signal processors, to perform a wide variety of signal processing operations. The digital signals processed in this manner are a sequence of numbers that represent Sampling (signal processing), samples of a continuous variable in a domain such as time, space, or frequency. In digital electronics, a digital signal is represented as a pulse train, which is typically generated by the switching of a transistor. Digital signal processing and analog signal processing are subfields of signal processing. DSP applications include Audio signal processing, audio and speech processing, sonar, radar and other sensor array processing, spectral density estimation, statistical signal processing, digital image processing, data compression, video coding, audio coding, image compression, signal processing for telecommunications, control systems, biomedical engineering, and seismology ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Zeros And Poles
In complex analysis (a branch of mathematics), a pole is a certain type of singularity of a complex-valued function of a complex variable. It is the simplest type of non- removable singularity of such a function (see essential singularity). Technically, a point is a pole of a function if it is a zero of the function and is holomorphic (i.e. complex differentiable) in some neighbourhood of . A function is meromorphic in an open set if for every point of there is a neighborhood of in which at least one of and is holomorphic. If is meromorphic in , then a zero of is a pole of , and a pole of is a zero of . This induces a duality between ''zeros'' and ''poles'', that is fundamental for the study of meromorphic functions. For example, if a function is meromorphic on the whole complex plane plus the point at infinity, then the sum of the multiplicities of its poles equals the sum of the multiplicities of its zeros. Definitions A function of a complex variable ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Block Diagram For The Explicit Formula For Lagrange Interpolation Coefficients
Block or blocked may refer to: Arts, entertainment and media Broadcasting * Block programming, the result of a programming strategy in broadcasting * W242BX, a radio station licensed to Greenville, South Carolina, United States known as ''96.3 the Block '' * WFNZ-FM, a radio station licensed to Harrisburg, North Carolina, United States, branded as ''92.7 The Block'' * "Blocked", an episode of the television series ''The Flash'' Music * Block Entertainment, a record label * Blocks Recording Club, a record label * Woodblock (instrument), a small piece of slit drum made from one piece of wood and used as a percussion instrument * "Blocks", by C418 from ''Minecraft – Volume Beta'', 2013 Toys * Toy block, one of a set of wooden or plastic pieces, of various shapes * Unit block, a type of standardized wooden toy block for children Video games * Blocked (video game), a puzzle game for the iPhone and iPod Touch Building and construction * Concrete block, cinder block or cement b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lagrange Polynomial
In numerical analysis, the Lagrange interpolating polynomial is the unique polynomial of lowest degree that interpolates a given set of data. Given a data set of coordinate pairs (x_j, y_j) with 0 \leq j \leq k, the x_j are called ''nodes'' and the y_j are called ''values''. The Lagrange polynomial L(x) has degree \leq k and assumes each value at the corresponding node, L(x_j) = y_j. Although named after Joseph-Louis Lagrange, who published it in 1795, the method was first discovered in 1779 by Edward Waring. It is also an easy consequence of a formula published in 1783 by Leonhard Euler. Uses of Lagrange polynomials include the Newton–Cotes method of numerical integration, Shamir's secret sharing scheme in cryptography, and Reed–Solomon error correction in coding theory. For equispaced nodes, Lagrange interpolation is susceptible to Runge's phenomenon of large oscillation. Definition Given a set of k + 1 nodes \, which must all be distinct, x_j \neq x_m for ind ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Least Squares
The method of least squares is a mathematical optimization technique that aims to determine the best fit function by minimizing the sum of the squares of the differences between the observed values and the predicted values of the model. The method is widely used in areas such as regression analysis, curve fitting and data modeling. The least squares method can be categorized into linear and nonlinear forms, depending on the relationship between the model parameters and the observed data. The method was first proposed by Adrien-Marie Legendre in 1805 and further developed by Carl Friedrich Gauss. History Founding The method of least squares grew out of the fields of astronomy and geodesy, as scientists and mathematicians sought to provide solutions to the challenges of navigating the Earth's oceans during the Age of Discovery. The accurate description of the behavior of celestial bodies was the key to enabling ships to sail in open seas, where sailors could no longer rely on la ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sampling Of Continuous-time Domain Sinc Function At Various Fractional Delay Values
Sampling may refer to: *Sampling (signal processing), converting a continuous signal into a discrete signal * Sampling (graphics), converting continuous colors into discrete color components *Sampling (music), the reuse of a sound recording in another recording **Sampler (musical instrument), an electronic musical instrument used to record and play back samples *Sampling (statistics), selection of observations to acquire some knowledge of a statistical population * Sampling (case studies), selection of cases for single or multiple case studies * Sampling (audit), application of audit procedures to less than 100% of population to be audited *Sampling (medicine), gathering of matter from the body to aid in the process of a medical diagnosis and/or evaluation of an indication for treatment, further medical tests or other procedures. *Sampling (occupational hygiene), detection of hazardous materials in the workplace *Sampling (for testing or analysis), taking a representative portion of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sinc Function
In mathematics, physics and engineering, the sinc function ( ), denoted by , has two forms, normalized and unnormalized.. In mathematics, the historical unnormalized sinc function is defined for by \operatorname(x) = \frac. Alternatively, the unnormalized sinc function is often called the sampling function, indicated as Sa(''x''). In digital signal processing and information theory, the normalized sinc function is commonly defined for by \operatorname(x) = \frac. In either case, the value at is defined to be the limiting value \operatorname(0) := \lim_\frac = 1 for all real (the limit can be proven using the squeeze theorem). The normalization causes the definite integral of the function over the real numbers to equal 1 (whereas the same integral of the unnormalized sinc function has a value of ). As a further useful property, the zeros of the normalized sinc function are the nonzero integer values of . The normalized sinc function is the Fourier transform of the r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Infinite Impulse Response
Infinite impulse response (IIR) is a property applying to many linear time-invariant systems that are distinguished by having an impulse response h(t) that does not become exactly zero past a certain point but continues indefinitely. This is in contrast to a finite impulse response (FIR) system, in which the impulse response ''does'' become exactly zero at times t>T for some finite T, thus being of finite duration. Common examples of linear time-invariant systems are most electronic and digital filters. Systems with this property are known as ''IIR systems'' or ''IIR filters''. In practice, the impulse response, even of IIR systems, usually approaches zero and can be neglected past a certain point. However the physical systems which give rise to IIR or FIR responses are dissimilar, and therein lies the importance of the distinction. For instance, analog electronic filters composed of resistors, capacitors, and/or inductors (and perhaps linear amplifiers) are generally IIR filte ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Causal Filter
In signal processing, a causal filter is a linear and time-invariant causal system. The word ''causal'' indicates that the filter output depends only on past and present inputs. A filter whose output also depends on future inputs is non-causal, whereas a filter whose output depends ''only'' on future inputs is anti-causal. Systems (including filters) that are ''realizable'' (i.e. that operate in real time) must be causal because such systems cannot act on a future input. In effect that means the output sample that best represents the input at time t, comes out slightly later. A common design practice for digital filters is to create a realizable filter by shortening and/or time-shifting a non-causal impulse response. If shortening is necessary, it is often accomplished as the product of the impulse-response with a window function. An example of an anti-causal filter is a maximum phase filter, which can be defined as a stable, anti-causal filter whose inverse is also stable and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Filter Design
Filter design is the process of designing a signal processing filter that satisfies a set of requirements, some of which may be conflicting. The purpose is to find a realization of the filter that meets each of the requirements to an acceptable degree. The filter design process can be described as an optimization problem. Certain parts of the design process can be automated, but an experienced designer may be needed to get a good result. The design of digital filters is a complex topic. Although filters are easily understood and calculated, the practical challenges of their design and implementation are significant and are the subject of advanced research. Typical design requirements Typical requirements which may be considered in the design process are: * Frequency response * Phase shift or group delay * impulse response * Causal filter required? * Stable filter required? * Finite (in duration) impulse response required? * Computational complexity * Technology The f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dirac Delta Function
In mathematical analysis, the Dirac delta function (or distribution), also known as the unit impulse, is a generalized function on the real numbers, whose value is zero everywhere except at zero, and whose integral over the entire real line is equal to one. Thus it can be Heuristic, represented heuristically as \delta (x) = \begin 0, & x \neq 0 \\ , & x = 0 \end such that \int_^ \delta(x) dx=1. Since there is no function having this property, modelling the delta "function" rigorously involves the use of limit (mathematics), limits or, as is common in mathematics, measure theory and the theory of distribution (mathematics), distributions. The delta function was introduced by physicist Paul Dirac, and has since been applied routinely in physics and engineering to model point masses and instantaneous impulses. It is called the delta function because it is a continuous analogue of the Kronecker delta function, which is usually defined on a discrete domain and takes values ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |