|
Multiple Correlation
In statistics, the coefficient of multiple correlation is a measure of how well a given variable can be predicted using a linear function of a set of other variables. It is the correlation between the variable's values and the best predictions that can be computed linearly from the predictive variables. The coefficient of multiple correlation takes values between 0 and 1. Higher values indicate higher predictability of the dependent variable from the independent variables, with a value of 1 indicating that the predictions are exactly correct and a value of 0 indicating that no linear combination of the independent variables is a better predictor than is the fixed mean of the dependent variable. The coefficient of multiple correlation is known as the square root of the coefficient of determination, but under the particular assumptions that an intercept is included and that the best possible linear predictors are used, whereas the coefficient of determination is defined for more ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Statistics
Statistics (from German language, German: ', "description of a State (polity), state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a scientific, industrial, or social problem, it is conventional to begin with a statistical population or a statistical model to be studied. Populations can be diverse groups of people or objects such as "all people living in a country" or "every atom composing a crystal". Statistics deals with every aspect of data, including the planning of data collection in terms of the design of statistical survey, surveys and experimental design, experiments. When census data (comprising every member of the target population) cannot be collected, statisticians collect data by developing specific experiment designs and survey sample (statistics), samples. Representative sampling assures that inferences and conclusions can reasonably extend from the sample ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
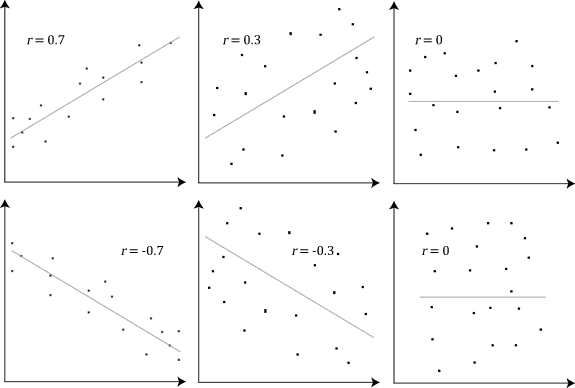
Correlation
In statistics, correlation or dependence is any statistical relationship, whether causal or not, between two random variables or bivariate data. Although in the broadest sense, "correlation" may indicate any type of association, in statistics it usually refers to the degree to which a pair of variables are '' linearly'' related. Familiar examples of dependent phenomena include the correlation between the height of parents and their offspring, and the correlation between the price of a good and the quantity the consumers are willing to purchase, as it is depicted in the demand curve. Correlations are useful because they can indicate a predictive relationship that can be exploited in practice. For example, an electrical utility may produce less power on a mild day based on the correlation between electricity demand and weather. In this example, there is a causal relationship, because extreme weather causes people to use more electricity for heating or cooling. However, in g ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Correlation And Dependence
In statistics, correlation or dependence is any statistical relationship, whether causal or not, between two random variables or bivariate data. Although in the broadest sense, "correlation" may indicate any type of association, in statistics it usually refers to the degree to which a pair of variables are '' linearly'' related. Familiar examples of dependent phenomena include the correlation between the height of parents and their offspring, and the correlation between the price of a good and the quantity the consumers are willing to purchase, as it is depicted in the demand curve. Correlations are useful because they can indicate a predictive relationship that can be exploited in practice. For example, an electrical utility may produce less power on a mild day based on the correlation between electricity demand and weather. In this example, there is a causal relationship, because extreme weather causes people to use more electricity for heating or cooling. However, in gen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Expected Value
In probability theory, the expected value (also called expectation, expectancy, expectation operator, mathematical expectation, mean, expectation value, or first Moment (mathematics), moment) is a generalization of the weighted average. Informally, the expected value is the arithmetic mean, mean of the possible values a random variable can take, weighted by the probability of those outcomes. Since it is obtained through arithmetic, the expected value sometimes may not even be included in the sample data set; it is not the value you would expect to get in reality. The expected value of a random variable with a finite number of outcomes is a weighted average of all possible outcomes. In the case of a continuum of possible outcomes, the expectation is defined by Integral, integration. In the axiomatic foundation for probability provided by measure theory, the expectation is given by Lebesgue integration. The expected value of a random variable is often denoted by , , or , with a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Total Sum Of Squares
In statistical data analysis the total sum of squares (TSS or SST) is a quantity that appears as part of a standard way of presenting results of such analyses. For a set of observations, y_i, i\leq n, it is defined as the sum over all squared differences between the observations and their overall mean \bar.:Everitt, B.S. (2002) ''The Cambridge Dictionary of Statistics'', CUP, :\mathrm=\sum_^\left(y_-\bar\right)^2 For wide classes of linear models, the total sum of squares equals the explained sum of squares plus the residual sum of squares. For proof of this in the multivariate OLS case, see partitioning in the general OLS model. In analysis of variance (ANOVA) the total sum of squares is the sum of the so-called "within-samples" sum of squares and "between-samples" sum of squares, i.e., partitioning of the sum of squares. In multivariate analysis of variance (MANOVA) the following equation applies Especially chapters 11 and 12. :\mathbf = \mathbf + \mathbf, g where T is th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Sum Of Squares Of Residuals
In statistics, the residual sum of squares (RSS), also known as the sum of squared residuals (SSR) or the sum of squared estimate of errors (SSE), is the sum of the squares of residuals (deviations predicted from actual empirical values of data). It is a measure of the discrepancy between the data and an estimation model, such as a linear regression. A small RSS indicates a tight fit of the model to the data. It is used as an optimality criterion in parameter selection and model selection. In general, total sum of squares = explained sum of squares + residual sum of squares. For a proof of this in the multivariate ordinary least squares (OLS) case, see partitioning in the general OLS model. One explanatory variable In a model with a single explanatory variable, RSS is given by: :\operatorname = \sum_^n (y_i - f(x_i))^2 where ''y''''i'' is the ''i''th value of the variable to be predicted, ''x''''i'' is the ''i''th value of the explanatory variable, and f(x_i) is the p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Matrix Inversion
In linear algebra, an invertible matrix (''non-singular'', ''non-degenarate'' or ''regular'') is a square matrix that has an inverse. In other words, if some other matrix is multiplied by the invertible matrix, the result can be multiplied by an inverse to undo the operation. An invertible matrix multiplied by its inverse yields the identity matrix. Invertible matrices are the same size as their inverse. Definition An -by- square matrix is called invertible if there exists an -by- square matrix such that\mathbf = \mathbf = \mathbf_n ,where denotes the -by- identity matrix and the multiplication used is ordinary matrix multiplication. If this is the case, then the matrix is uniquely determined by , and is called the (multiplicative) ''inverse'' of , denoted by . Matrix inversion is the process of finding the matrix which when multiplied by the original matrix gives the identity matrix. Over a field, a square matrix that is ''not'' invertible is called singular or degenerat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Transpose
In linear algebra, the transpose of a Matrix (mathematics), matrix is an operator which flips a matrix over its diagonal; that is, it switches the row and column indices of the matrix by producing another matrix, often denoted by (among other notations). The transpose of a matrix was introduced in 1858 by the British mathematician Arthur Cayley. Transpose of a matrix Definition The transpose of a matrix , denoted by , , , A^, , , or , may be constructed by any one of the following methods: #Reflection (mathematics), Reflect over its main diagonal (which runs from top-left to bottom-right) to obtain #Write the rows of as the columns of #Write the columns of as the rows of Formally, the -th row, -th column element of is the -th row, -th column element of : :\left[\mathbf^\operatorname\right]_ = \left[\mathbf\right]_. If is an matrix, then is an matrix. In the case of square matrices, may also denote the th power of the matrix . For avoiding a possibl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Correlation Matrix
In statistics, correlation or dependence is any statistical relationship, whether causal or not, between two random variables or bivariate data. Although in the broadest sense, "correlation" may indicate any type of association, in statistics it usually refers to the degree to which a pair of variables are '' linearly'' related. Familiar examples of dependent phenomena include the correlation between the height of parents and their offspring, and the correlation between the price of a good and the quantity the consumers are willing to purchase, as it is depicted in the demand curve. Correlations are useful because they can indicate a predictive relationship that can be exploited in practice. For example, an electrical utility may produce less power on a mild day based on the correlation between electricity demand and weather. In this example, there is a causal relationship, because extreme weather causes people to use more electricity for heating or cooling. However, in ge ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Euclidean Space
Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, in Euclid's ''Elements'', it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are ''Euclidean spaces'' of any positive integer dimension ''n'', which are called Euclidean ''n''-spaces when one wants to specify their dimension. For ''n'' equal to one or two, they are commonly called respectively Euclidean lines and Euclidean planes. The qualifier "Euclidean" is used to distinguish Euclidean spaces from other spaces that were later considered in physics and modern mathematics. Ancient Greek geometers introduced Euclidean space for modeling the physical space. Their work was collected by the ancient Greek mathematician Euclid in his ''Elements'', with the great innovation of '' proving'' all properties of the space as theorems, by starting from a few fundamental properties, called '' postulates'', which either were considered as evid ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Linear Function
In mathematics, the term linear function refers to two distinct but related notions: * In calculus and related areas, a linear function is a function whose graph is a straight line, that is, a polynomial function of degree zero or one. For distinguishing such a linear function from the other concept, the term ''affine function'' is often used. * In linear algebra, mathematical analysis, and functional analysis, a linear function is a linear map. As a polynomial function In calculus, analytic geometry and related areas, a linear function is a polynomial of degree one or less, including the zero polynomial (the latter not being considered to have degree zero). When the function is of only one variable, it is of the form :f(x)=ax+b, where and are constants, often real numbers. The graph of such a function of one variable is a nonvertical line. is frequently referred to as the slope of the line, and as the intercept. If ''a > 0'' then the gradient is positive an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Y-intercept
In analytic geometry, using the common convention that the horizontal axis represents a variable x and the vertical axis represents a variable y, a y-intercept or vertical intercept is a point where the graph of a function or relation intersects the y-axis of the coordinate system. As such, these points satisfy x = 0. Using equations If the curve in question is given as y = f(x), the y-coordinate of the y-intercept is found by calculating f(0). Functions which are undefined at x = 0 have no y-intercept. If the function is linear and is expressed in slope-intercept form as f(x) = a + bx, the constant term a is the y-coordinate of the y-intercept. Multiple y-intercepts Some 2-dimensional mathematical relationships such as circles, ellipses, and hyperbolas can have more than one y-intercept. Because functions associate x-values to no more than one y-value as part of their definition, they can have at most one y-intercept. x-intercepts Analogously, an x-intercept is a point w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |