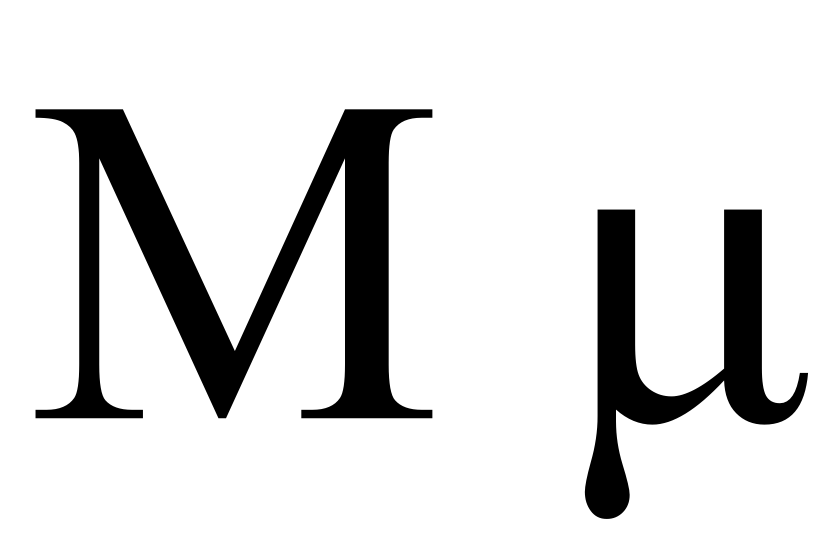|
Viscosity
The viscosity of a fluid is a measure of its resistance to deformation at a given rate. For liquids, it corresponds to the informal concept of "thickness": for example, syrup has a higher viscosity than water. Viscosity quantifies the internal frictional force between adjacent layers of fluid that are in relative motion. For instance, when a viscous fluid is forced through a tube, it flows more quickly near the tube's axis than near its walls. Experiments show that some stress (such as a pressure difference between the two ends of the tube) is needed to sustain the flow. This is because a force is required to overcome the friction between the layers of the fluid which are in relative motion. For a tube with a constant rate of flow, the strength of the compensating force is proportional to the fluid's viscosity. In general, viscosity depends on a fluid's state, such as its temperature, pressure, and rate of deformation. However, the dependence on some of these properties is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Viscosities
The viscosity of a fluid is a measure of its drag (physics), resistance to deformation at a given rate. For liquids, it corresponds to the informal concept of "thickness": for example, syrup has a higher viscosity than water. Viscosity quantifies the internal friction, frictional force between adjacent layers of fluid that are in relative motion. For instance, when a viscous fluid is forced through a tube, it flows more quickly near the tube's axis than near its walls. Experiments show that some stress (physics), stress (such as a pressure difference between the two ends of the tube) is needed to sustain the flow. This is because a force is required to overcome the friction between the layers of the fluid which are in relative motion. For a tube with a constant rate of flow, the strength of the compensating force is proportional to the fluid's viscosity. In general, viscosity depends on a fluid's state, such as its temperature, pressure, and rate of deformation. However, the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Newtonian Fluid
A Newtonian fluid is a fluid in which the viscous stresses arising from its flow are at every point linearly correlated to the local strain rate — the rate of change of its deformation over time. Stresses are proportional to the rate of change of the fluid's velocity vector. A fluid is Newtonian only if the tensors that describe the viscous stress and the strain rate are related by a constant viscosity tensor that does not depend on the stress state and velocity of the flow. If the fluid is also isotropic (mechanical properties are the same along any direction), the viscosity tensor reduces to two real coefficients, describing the fluid's resistance to continuous shear deformation and continuous compression or expansion, respectively. Newtonian fluids are the simplest mathematical models of fluids that account for viscosity. While no real fluid fits the definition perfectly, many common liquids and gases, such as water and air, can be assumed to be Newtonian for practical c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Drag (physics)
In fluid dynamics, drag (sometimes called air resistance, a type of friction, or fluid resistance, another type of friction or fluid friction) is a force acting opposite to the relative motion of any object moving with respect to a surrounding fluid. This can exist between two fluid layers (or surfaces) or between a fluid and a solid surface. Unlike other resistive forces, such as dry friction, which are nearly independent of velocity, the drag force depends on velocity. Drag force is proportional to the velocity for low-speed flow and the squared velocity for high speed flow, where the distinction between low and high speed is measured by the Reynolds number. Even though the ultimate cause of drag is viscous friction, turbulent drag is independent of viscosity. Drag forces always tend to decrease fluid velocity relative to the solid object in the fluid's path. Examples Examples of drag include the component of the net aerodynamic or hydrodynamic force acting opposite to the di ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Shear Stress
Shear stress, often denoted by (Greek: tau), is the component of stress coplanar with a material cross section. It arises from the shear force, the component of force vector parallel to the material cross section. ''Normal stress'', on the other hand, arises from the force vector component perpendicular to the material cross section on which it acts. General shear stress The formula to calculate average shear stress is force per unit area.: : \tau = , where: : = the shear stress; : = the force applied; : = the cross-sectional area of material with area parallel to the applied force vector. Other forms Wall shear stress Wall shear stress expresses the retarding force (per unit area) from a wall in the layers of a fluid flowing next to the wall. It is defined as: \tau_w:=\mu\left(\frac\right)_ Where \mu is the dynamic viscosity, u the flow velocity and y the distance from the wall. It is used, for example, in the description of arterial blood flow in which case which ther ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fluid
In physics, a fluid is a liquid, gas, or other material that continuously deforms (''flows'') under an applied shear stress, or external force. They have zero shear modulus, or, in simpler terms, are substances which cannot resist any shear force applied to them. Although the term ''fluid'' generally includes both the liquid and gas phases, its definition varies among branches of science. Definitions of ''solid'' vary as well, and depending on field, some substances can be both fluid and solid. Viscoelastic fluids like Silly Putty appear to behave similar to a solid when a sudden force is applied. Substances with a very high viscosity such as pitch appear to behave like a solid (see pitch drop experiment) as well. In particle physics, the concept is extended to include fluidic matters other than liquids or gases. A fluid in medicine or biology refers any liquid constituent of the body (body fluid), whereas "liquid" is not used in this sense. Sometimes liquids given for flui ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Friction
Friction is the force resisting the relative motion of solid surfaces, fluid layers, and material elements sliding against each other. There are several types of friction: *Dry friction is a force that opposes the relative lateral motion of two solid surfaces in contact. Dry friction is subdivided into ''static friction'' ("stiction") between non-moving surfaces, and ''kinetic friction'' between moving surfaces. With the exception of atomic or molecular friction, dry friction generally arises from the interaction of surface features, known as asperities (see Figure 1). *Fluid friction describes the friction between layers of a viscous fluid that are moving relative to each other. *Lubricated friction is a case of fluid friction where a lubricant fluid separates two solid surfaces. *Skin friction is a component of drag, the force resisting the motion of a fluid across the surface of a body. *Internal friction is the force resisting motion between the elements making up a so ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stress (mechanics)
In continuum mechanics, stress is a physical quantity. It is a quantity that describes the magnitude of forces that cause deformation. Stress is defined as ''force per unit area''. When an object is pulled apart by a force it will cause elongation which is also known as deformation, like the stretching of an elastic band, it is called tensile stress. But, when the forces result in the compression of an object, it is called compressive stress. It results when forces like tension or compression act on a body. The greater this force and the smaller the cross-sectional area of the body on which it acts, the greater the stress. Therefore, stress is measured in newton per square meter (N/m2) or pascal (Pa). Stress expresses the internal forces that neighbouring particles of a continuous material exert on each other, while strain is the measure of the deformation of the material. For example, when a solid vertical bar is supporting an overhead weight, each particle in the bar pushe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Glue
Adhesive, also known as glue, cement, mucilage, or paste, is any non-metallic substance applied to one or both surfaces of two separate items that binds them together and resists their separation. The use of adhesives offers certain advantages over other binding techniques such as sewing, mechanical fastenings, or welding. These include the ability to bind different materials together, the more efficient distribution of stress across a joint, the cost-effectiveness of an easily mechanized process, and greater flexibility in design. Disadvantages of adhesive use include decreased stability at high temperatures, relative weakness in bonding large objects with a small bonding surface area, and greater difficulty in separating objects during testing. Adhesives are typically organized by the method of adhesion followed by ''reactive'' or ''non-reactive'', a term which refers to whether the adhesive chemically reacts in order to harden. Alternatively, they can be organized eithe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stress (physics)
In continuum mechanics, stress is a physical quantity. It is a quantity that describes the magnitude of forces that cause deformation. Stress is defined as ''force per unit area''. When an object is pulled apart by a force it will cause elongation which is also known as deformation, like the stretching of an elastic band, it is called tensile stress. But, when the forces result in the compression of an object, it is called compressive stress. It results when forces like Tension (physics), tension or Compression (physics), compression act on a body. The greater this force and the smaller the cross-sectional area of the body on which it acts, the greater the stress. Therefore, stress is measured in newton per square meter (N/m2) or pascal (Pa). Stress expresses the internal forces that neighbouring particles of a continuous material exert on each other, while deformation (mechanics)#Strain, strain is the measure of the deformation of the material. For example, when a solid vertic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pressure
Pressure (symbol: ''p'' or ''P'') is the force applied perpendicular to the surface of an object per unit area over which that force is distributed. Gauge pressure (also spelled ''gage'' pressure)The preferred spelling varies by country and even by industry. Further, both spellings are often used ''within'' a particular industry or country. Industries in British English-speaking countries typically use the "gauge" spelling. is the pressure relative to the ambient pressure. Various units are used to express pressure. Some of these derive from a unit of force divided by a unit of area; the SI unit of pressure, the pascal (Pa), for example, is one newton per square metre (N/m2); similarly, the pound-force per square inch (psi) is the traditional unit of pressure in the imperial and U.S. customary systems. Pressure may also be expressed in terms of standard atmospheric pressure; the atmosphere (atm) is equal to this pressure, and the torr is defined as of this. Manometric u ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mu (letter)
Mu (uppercase Μ, lowercase μ; Ancient Greek , ell, μι or μυ—both ) is the 12th letter of the Greek alphabet, representing the voiced bilabial nasal . In the system of Greek numerals it has a value of 40. Mu was derived from the Egyptian hieroglyphic symbol for water, which had been simplified by the Phoenicians and named after their word for water, to become 𐤌 (mem). Letters that derive from mu include the Roman M and the Cyrillic М. Names Ancient Greek In Ancient Greek, the name of the letter was written and pronounced Modern Greek In Modern Greek, the letter is spelled and pronounced . In polytonic orthography, it is written with an acute accent: . Use as symbol The lowercase letter mu (μ) is used as a special symbol in many academic fields. Uppercase mu is not used, because it appears identical to Latin M. Measurement *the SI prefix ''micro-'', which represents one millionth, or 10−6. Lowercase letter "u" is often substituted for "μ" w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Eta (letter)
Eta (uppercase , lowercase ; grc, ἦτα ''ē̂ta'' or ell, ήτα ''ita'' ) is the seventh letter of the Greek alphabet, representing the close front unrounded vowel . Originally denoting the voiceless glottal fricative in most dialects, its sound value in the classical Attic dialect of Ancient Greek was a long open-mid front unrounded vowel , raised to in hellenistic Greek, a process known as iotacism or itacism. In the ancient Attic number system (Herodianic or acrophonic numbers), the number 100 was represented by "", because it was the initial of , the ancient spelling of = "one hundred". In the later system of (Classical) Greek numerals eta represents 8. Eta was derived from the Phoenician letter heth . Letters that arose from eta include the Latin H and the Cyrillic letter И and Й. History Consonant h The letter shape 'H' was originally used in most Greek dialects to represent the voiceless glottal fricative . In this function, it was borrowed in the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |