|
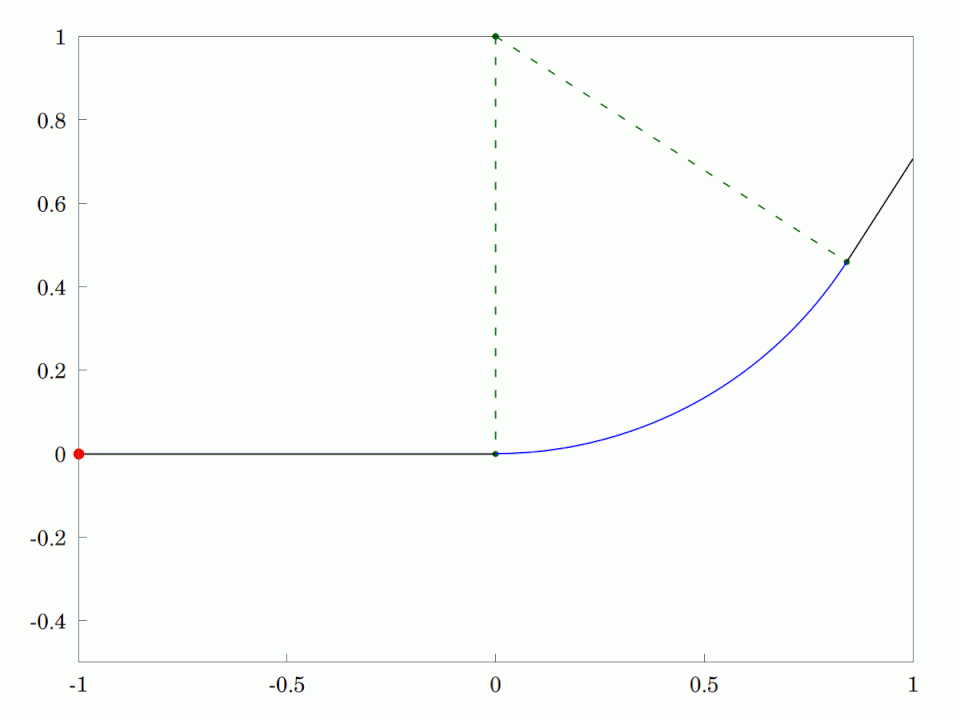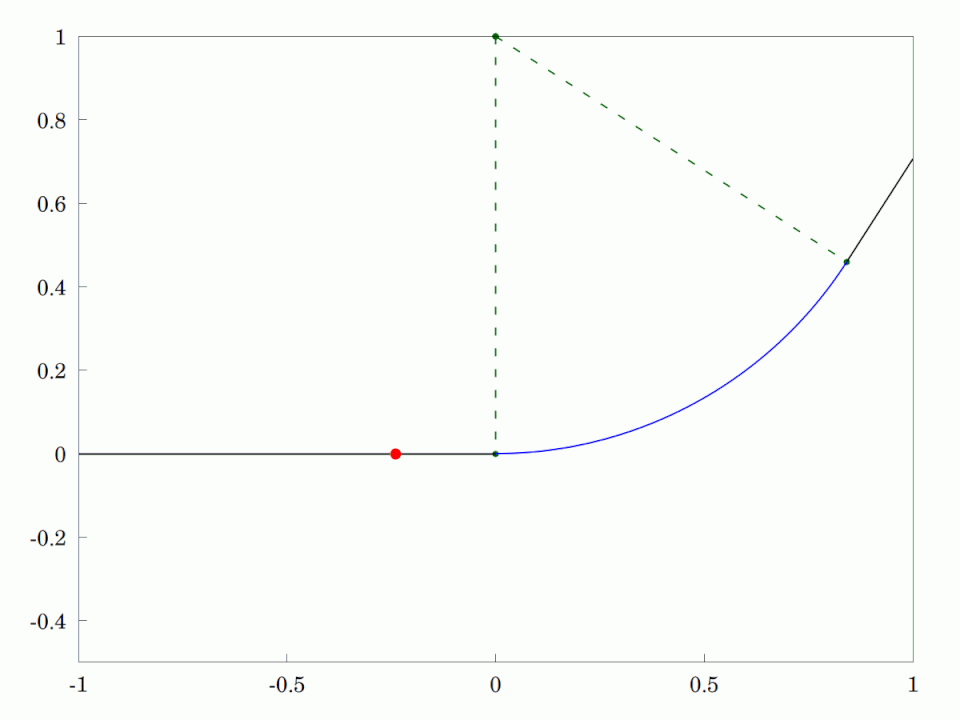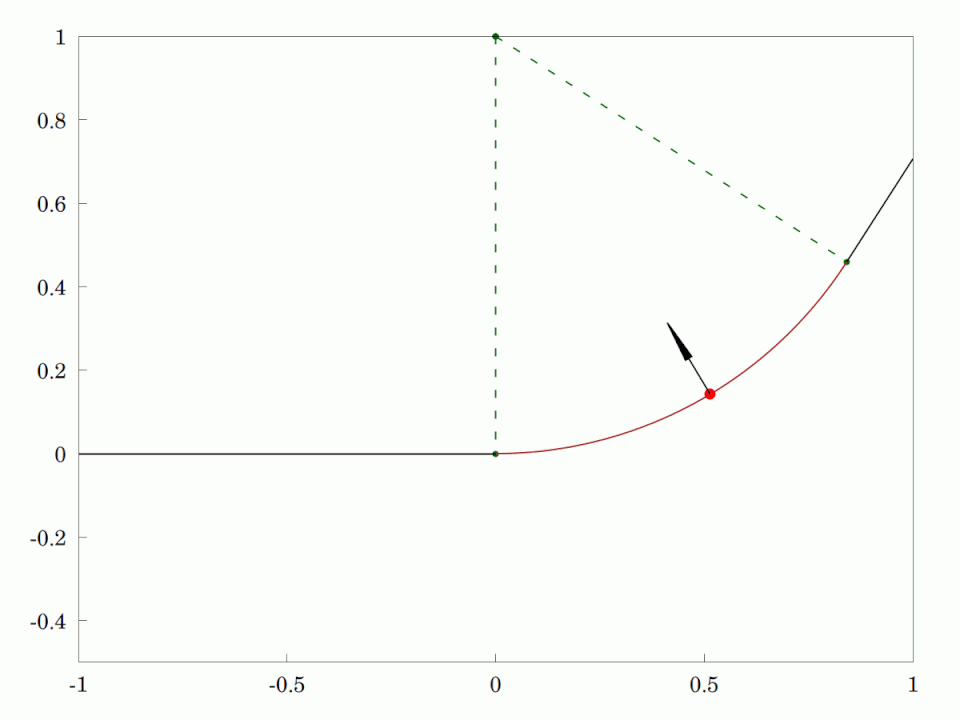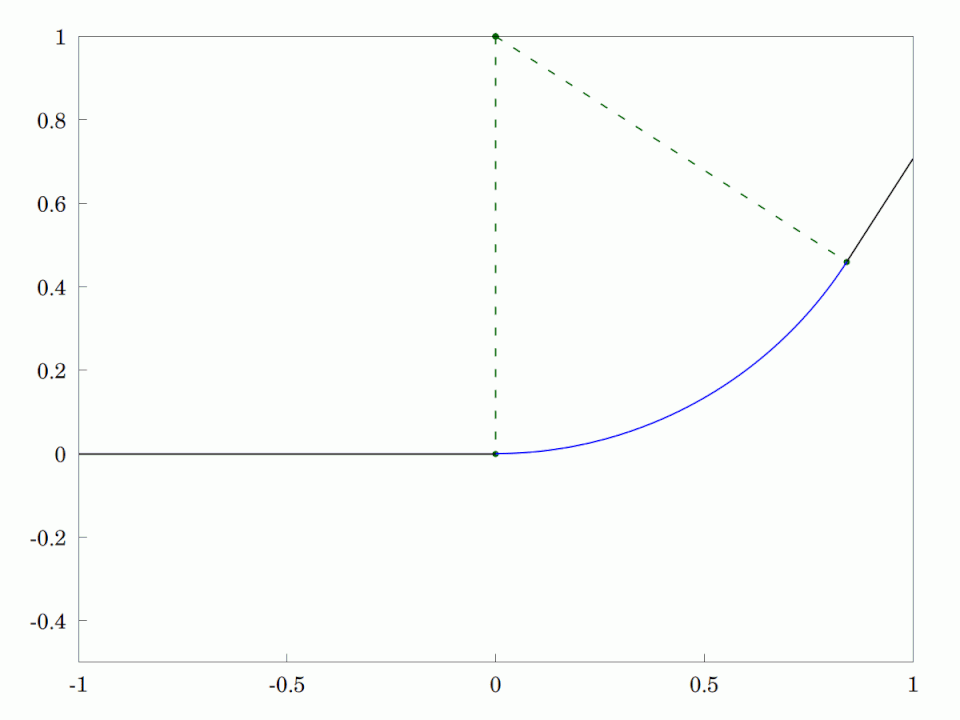
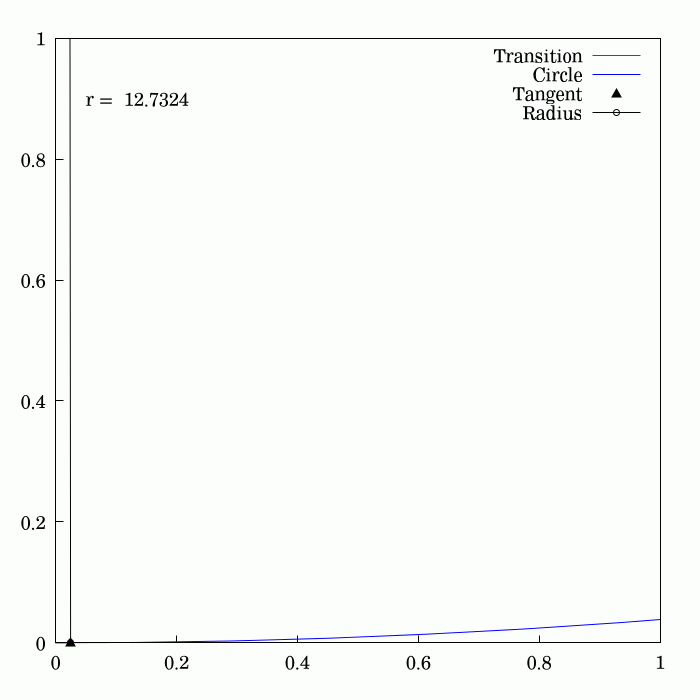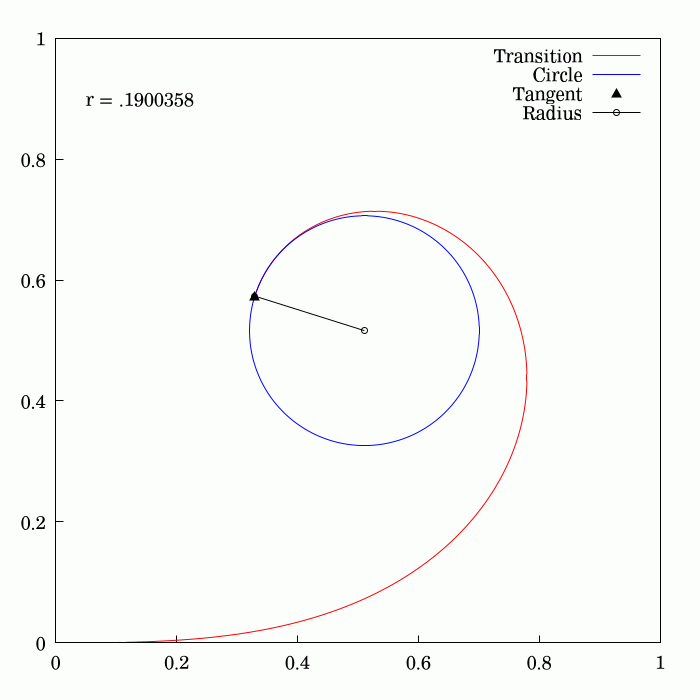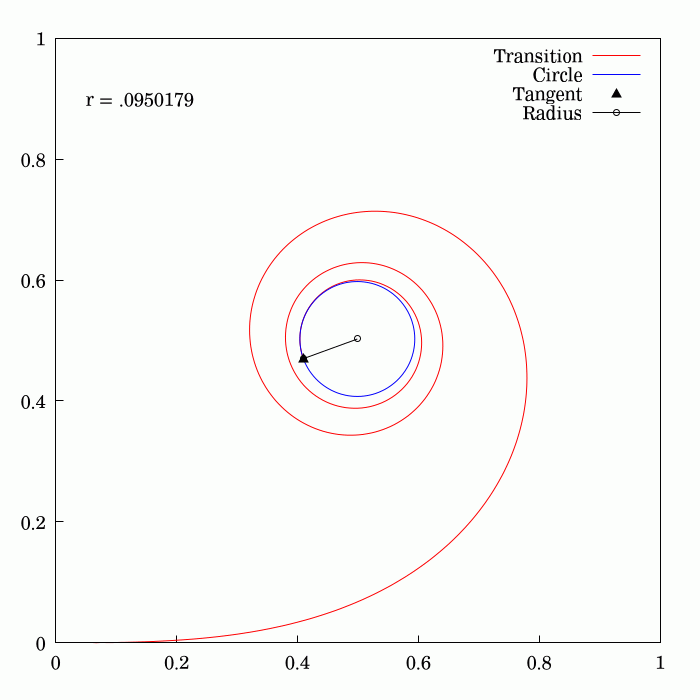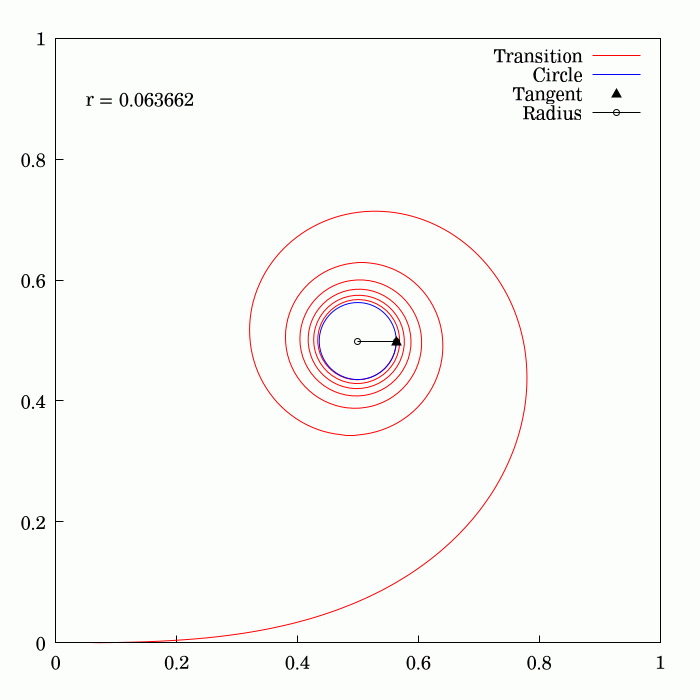
Track Transition Curve
A transition curve (also, spiral easement or, simply, spiral) is a spiral-shaped length of highway or track (rail transport), railroad track that is used between sections having different profiles and radii, such as between straightaways (tangents) and curves, or between two different curves. In the horizontal plane, the radius of a transition curve varies continually over its length between the disparate radii of the sections that it joins—for example, from infinite radius at a tangent to the nominal radius of a smooth curve. The resulting spiral provides a gradual, eased transition, preventing undesirable sudden, abrupt changes in centripetal acceleration, lateral (centripetal) acceleration that would otherwise occur without a transition curve. Similarly, on highways, transition curves allow drivers to change steering gradually when entering or exiting curves. Transition curves also serve as a transition in the vertical plane, whereby the elevation of the inside or outside ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Easement Curve
A transition curve (also, spiral easement or, simply, spiral) is a spiral-shaped length of highway or railroad track that is used between sections having different profiles and radii, such as between straightaways (tangents) and curves, or between two different curves. In the horizontal plane, the radius of a transition curve varies continually over its length between the disparate radii of the sections that it joins—for example, from infinite radius at a tangent to the nominal radius of a smooth curve. The resulting spiral provides a gradual, eased transition, preventing undesirable sudden, abrupt changes in lateral (centripetal) acceleration that would otherwise occur without a transition curve. Similarly, on highways, transition curves allow drivers to change steering gradually when entering or exiting curves. Transition curves also serve as a transition in the vertical plane, whereby the elevation of the inside or outside of the curve is lowered or raised to reach the n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Leonhard Euler
Leonhard Euler ( ; ; ; 15 April 170718 September 1783) was a Swiss polymath who was active as a mathematician, physicist, astronomer, logician, geographer, and engineer. He founded the studies of graph theory and topology and made influential discoveries in many other branches of mathematics, such as analytic number theory, complex analysis, and infinitesimal calculus. He also introduced much of modern mathematical terminology and Mathematical notation, notation, including the notion of a mathematical function. He is known for his work in mechanics, fluid dynamics, optics, astronomy, and music theory. Euler has been called a "universal genius" who "was fully equipped with almost unlimited powers of imagination, intellectual gifts and extraordinary memory". He spent most of his adult life in Saint Petersburg, Russia, and in Berlin, then the capital of Kingdom of Prussia, Prussia. Euler is credited for popularizing the Greek letter \pi (lowercase Pi (letter), pi) to denote Pi, th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Minimum Railway Curve Radius
The minimum railway curve radius is the shortest allowable design radius for the centerline of railway tracks under a particular set of conditions. It has an important bearing on construction costs and operating costs and, in combination with superelevation (difference in elevation of the two rails) in the case of train tracks, determines the maximum safe speed of a curve. The minimum radius of a curve is one parameter in the design of railway vehicles as well as trams; monorails and automated guideways are also subject to a minimum radius. History The first proper railway was the Liverpool and Manchester Railway, which opened in 1830. Like the tram roads that had preceded it over a hundred years, the L&M had gentle curves and gradients. Reasons for these gentle curves include the lack of strength of the track, which might have overturned if the curves were too sharp causing derailments. The gentler the curves, the greater the visibility, thus boosting safety via increa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Degree Of Curvature
Degree of curve or degree of curvature is a measure of curvature of a circular arc used in civil engineering for its easy use in layout surveying. Definition The Degree (angle), degree of curvature is defined as the central angle to the ends of an agreed length of either an Arc (curvature), arc or a Chord (geometry), chord; various lengths are commonly used in different areas of practice. This angle is also the Body relative direction, change in forward direction as that portion of the curve is traveled. In an ''n''-degree curve, the forward Bearing (angle), bearing changes by ''n'' degree (angle), degrees over the standard length of arc or chord. Usage Curvature is usually measured in radius of curvature. A small circle can be easily laid out by just using radius of curvature, but degree of curvature is more convenient for calculating and laying out the curve if the radius is as large as a kilometer or mile, as is needed for large scale works like roads and railroads. By using ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Fresnel Integral
250px, Plots of and . The maximum of is about . If the integrands of and were defined using instead of , then the image would be scaled vertically and horizontally (see below). The Fresnel integrals and are two transcendental functions named after Augustin-Jean Fresnel that are used in optics and are closely related to the error function (). They arise in the description of near-field Fresnel diffraction phenomena and are defined through the following integral representations: S(x) = \int_0^x \sin\left(t^2\right)\,dt, \quad C(x) = \int_0^x \cos\left(t^2\right)\,dt. The parametric curve is the Euler spiral or clothoid, a curve whose curvature varies linearly with arclength. The term Fresnel integral may also refer to the complex definite integral \int_^\infty e^ dx = \sqrte^ where is real and positive; this can be evaluated by closing a contour in the complex plane and applying Cauchy's integral theorem. Definition 250px, Fresnel integrals with arguments in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Cartesian Coordinates
In geometry, a Cartesian coordinate system (, ) in a plane is a coordinate system that specifies each point uniquely by a pair of real numbers called ''coordinates'', which are the signed distances to the point from two fixed perpendicular oriented lines, called '' coordinate lines'', ''coordinate axes'' or just ''axes'' (plural of ''axis'') of the system. The point where the axes meet is called the '' origin'' and has as coordinates. The axes directions represent an orthogonal basis. The combination of origin and basis forms a coordinate frame called the Cartesian frame. Similarly, the position of any point in three-dimensional space can be specified by three ''Cartesian coordinates'', which are the signed distances from the point to three mutually perpendicular planes. More generally, Cartesian coordinates specify the point in an -dimensional Euclidean space for any dimension . These coordinates are the signed distances from the point to mutually perpendicular fixed h ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Cant (road/rail)
The cant of a Rail transport, railway track or camber angle, camber of a road (also referred to as superelevation, cross slope or cross fall) is the rate of change in elevation (height) between the two rails or edges of the road. This is normally greater where the railway or road is curved; raising the outer rail or the outer edge of the road creates a banked turn, thus allowing vehicles to travel round the curve at greater speeds than would be possible if the surface were level. Rail Superelevation in railway tracks ;Importance of superelevation In curved railway tracks, the outer rail is elevated, providing a banked turn. This allows trains to navigate curves at higher speeds and reduces the pressure of the wheel flanges against the rails, minimizing friction and wear. The difference in elevation between the outer and inner rails is referred to as cant in most countries. ;How superelevation works The main functions of cant are the following: * Improve distribution of th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Circular Arc
A circular arc is the arc of a circle between a pair of distinct points. If the two points are not directly opposite each other, one of these arcs, the minor arc, subtends an angle at the center of the circle that is less than radians (180 degrees); and the other arc, the major arc, subtends an angle greater than radians. The arc of a circle is defined as the part or segment of the circumference of a circle. A straight line that connects the two ends of the arc is known as a '' chord'' of a circle. If the length of an arc is exactly half of the circle, it is known as a '' semicircular arc''. Length The length (more precisely, arc length) of an arc of a circle with radius ''r'' and subtending an angle ''θ'' (measured in radians) with the circle center — i.e., the central angle — is : L = \theta r. This is because :\frac=\frac. Substituting in the circumference :\frac=\frac, and, with ''α'' being the same angle measured in degrees, since ''θ'' = , the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Quadratic Equation
In mathematics, a quadratic equation () is an equation that can be rearranged in standard form as ax^2 + bx + c = 0\,, where the variable (mathematics), variable represents an unknown number, and , , and represent known numbers, where . (If and then the equation is linear equation, linear, not quadratic.) The numbers , , and are the ''coefficients'' of the equation and may be distinguished by respectively calling them, the ''quadratic coefficient'', the ''linear coefficient'' and the ''constant coefficient'' or ''free term''. The values of that satisfy the equation are called ''solution (mathematics), solutions'' of the equation, and ''zero of a function, roots'' or ''zero of a function, zeros'' of the quadratic function on its left-hand side. A quadratic equation has at most two solutions. If there is only one solution, one says that it is a double root. If all the coefficients are real numbers, there are either two real solutions, or a single real double root, or two comple ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
American Railway Engineering And Maintenance-of-Way Association
The American Railway Engineering and Maintenance-of-Way Association (AREMA) is a North American railway industry group. It publishes recommended practices for the design, construction and maintenance of railway infrastructure, which are used in the United States and Canada. Overview AREMA is headquartered in Lanham, Maryland, a suburb of Washington, D.C. As stated in their mission statement, AREMA promotes "The development and advancement of both technical and practical knowledge and recommended practices pertaining to the design, construction and maintenance of railway infrastructure." AREMA recognizes outstanding achievements in railway engineering with the annual William Walter Hay Award. Beth Caruso was appointed as AREMA's Executive Director/CEO in September 2015. Prior to this appointment, she served as AREMA's Director of Administration. Bill Riehl is the AREMA President and Chairman of the Board of Governors for 2024-25 History AREMA was established on October 1, 1997, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Three-dimensional Space
In geometry, a three-dimensional space (3D space, 3-space or, rarely, tri-dimensional space) is a mathematical space in which three values ('' coordinates'') are required to determine the position of a point. Most commonly, it is the three-dimensional Euclidean space, that is, the Euclidean space of dimension three, which models physical space. More general three-dimensional spaces are called '' 3-manifolds''. The term may also refer colloquially to a subset of space, a ''three-dimensional region'' (or 3D domain), a '' solid figure''. Technically, a tuple of numbers can be understood as the Cartesian coordinates of a location in a -dimensional Euclidean space. The set of these -tuples is commonly denoted \R^n, and can be identified to the pair formed by a -dimensional Euclidean space and a Cartesian coordinate system. When , this space is called the three-dimensional Euclidean space (or simply "Euclidean space" when the context is clear). In classical physics, it serve ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Track Geometry
Track geometry is concerned with the properties and relations of points, lines, curves, and surfaces in the three-dimensional positioning of railroad Track (rail transport), track. The term is also applied to measurements used in design, construction and maintenance of track. Track geometry involves standards, speed limits and other regulations in the areas of track gauge, alignment, elevation, curvature and track surface. Standards are usually separately expressed for Horizontal plane, horizontal and Vertical direction, vertical layouts although track geometry is three-dimensional. Layout Horizontal layout Horizontal layout is the track layout on the horizontal plane. This can be thought of as the Multiview orthographic projection#Plan, plan view which is a view of a 3-dimensional track from the position above the track. In track geometry, the horizontal layout involves the layout of three main track types: ''tangent track'' (straight line), ''curved track'', and ''track transit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |