|
Sundial
A sundial is a horological device that tells the time of day (referred to as civil time in modern usage) when direct sunlight shines by the apparent position of the Sun in the sky. In the narrowest sense of the word, it consists of a flat plate (the ''dial'') and a gnomon, which casts a shadow onto the dial. As the Sun appears to move through the sky, the shadow aligns with different hour-lines, which are marked on the dial to indicate the time of day. The ''style'' is the time-telling edge of the gnomon, though a single point or ''nodus'' may be used. The gnomon casts a broad shadow; the shadow of the style shows the time. The gnomon may be a rod, wire, or elaborately decorated metal casting. The style must be parallel to the axis of the Earth's rotation for the sundial to be accurate throughout the year. The style's angle from horizontal is equal to the sundial's geographical latitude. The term ''sundial'' can refer to any device that uses the Sun's altitude or azimut ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sundial Žiča
A sundial is a horological device that tells the time of day (referred to as civil time in modern usage) when direct sunlight shines by the apparent position of the Sun in the sky. In the narrowest sense of the word, it consists of a flat plate (the ''dial'') and a gnomon, which casts a shadow onto the dial. As the Sun appears to move through the sky, the shadow aligns with different hour-lines, which are marked on the dial to indicate the time of day. The ''style'' is the time-telling edge of the gnomon, though a single point or ''nodus'' may be used. The gnomon casts a broad shadow; the shadow of the style shows the time. The gnomon may be a rod, wire, or elaborately decorated metal casting. The style must be parallel to the axis of the Earth's rotation for the sundial to be accurate throughout the year. The style's angle from horizontal is equal to the sundial's geographical latitude. The term ''sundial'' can refer to any device that uses the Sun's altitude or azimuth ( ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gnomon
A gnomon (; ) is the part of a sundial that casts a shadow. The term is used for a variety of purposes in mathematics and other fields. History A painted stick dating from 2300 BC that was excavated at the astronomical site of Taosi is the oldest gnomon known in China. The gnomon was widely used in ancient China from the second century BC onward in order to determine the changes in seasons, orientation, and geographical latitude. The ancient Chinese used shadow measurements for creating calendars that are mentioned in several ancient texts. According to the collection of Zhou Chinese poetic anthologies ''Classic of Poetry'', one of the distant ancestors of King Wen of the Zhou dynasty used to measure gnomon shadow lengths to determine the orientation around the 14th century BC. The ancient Greek philosopher Anaximander (610–546 BC) is credited with introducing this Babylonian instrument to the Ancient Greeks. The ancient Greek mathematician and astronomer Oenopides used the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Daylight Saving Time
Daylight saving time (DST), also referred to as daylight savings time or simply daylight time (United States, Canada, and Australia), and summer time (United Kingdom, European Union, and others), is the practice of advancing clocks (typically by one hour) during warmer months so that darkness falls at a later clock time. The typical implementation of DST is to set clocks forward by one hour in the spring ("spring forward"), and to set clocks back by one hour in the fall ("fall back") to return to standard time. As a result, there is one 23-hour day in early spring and one 25-hour day in the middle of autumn. The idea of aligning waking hours to daylight hours to conserve candles was first proposed in 1784 by U.S. polymath Benjamin Franklin. In a satirical letter to the editor of ''The Journal of Paris'', Franklin suggested that waking up earlier in the summer would economize on candle usage; and calculated considerable savings. In 1895, New Zealand entomologist and astronome ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Analemmatic Sundial
Analemmatic sundials are a type of horizontal sundial that has a vertical gnomon and hour markers positioned in an elliptical pattern. The gnomon is not fixed and must change position daily to accurately indicate time of day. Hence there are no hour lines on the dial and the time of day is read only on the ellipse."Analemmatic sundials: How to build one and why they work" C.J. Budd and C.J. Sangwin, maths.org, 1 June 2000 As with most sundials, analemmatic sundials mark rather than clock time. Description An analemmatic sundial is completely defined by # The size of its ellipse (chosen by the designer). # The latitude of i ...[...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Position Of The Sun
The position of the Sun in the sky is a function of both the time and the geographic location of observation on Earth's surface. As Earth orbits the Sun over the course of a year, the Sun appears to move with respect to the fixed stars on the celestial sphere, along a circular path called the ecliptic. Earth's rotation about its axis causes diurnal motion, so that the Sun appears to move across the sky in a Sun path that depends on the observer's geographic latitude. The time when the Sun transits the observer's meridian depends on the geographic longitude. To find the Sun's position for a given location at a given time, one may therefore proceed in three steps as follows: # calculate the Sun's position in the ecliptic coordinate system, # convert to the equatorial coordinate system, and # convert to the horizontal coordinate system, for the observer's local time and location. This is the coordinate system normally used to calculate the position of the Sun in terms of solar zen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Equation Of Time
In mathematics, an equation is a formula that expresses the equality of two expressions, by connecting them with the equals sign . The word ''equation'' and its cognates in other languages may have subtly different meanings; for example, in French an ''équation'' is defined as containing one or more variables, while in English, any well-formed formula consisting of two expressions related with an equals sign is an equation. ''Solving'' an equation containing variables consists of determining which values of the variables make the equality true. The variables for which the equation has to be solved are also called unknowns, and the values of the unknowns that satisfy the equality are called solutions of the equation. There are two kinds of equations: identities and conditional equations. An identity is true for all values of the variables. A conditional equation is only true for particular values of the variables. An equation is written as two expressions, connected by ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Solar Time
Solar time is a calculation of the passage of time based on the position of the Sun in the sky. The fundamental unit of solar time is the day, based on the synodic rotation period. Two types of solar time are apparent solar time (sundial time) and mean solar time (clock time). Introduction A tall pole vertically fixed in the ground casts a shadow on any sunny day. At one moment during the day, the shadow will point exactly north or south (or disappear when and if the Sun moves directly overhead). That instant is local apparent noon, or 12:00 local apparent time. About 24 hours later the shadow will again point north–south, the Sun seeming to have covered a 360-degree arc around Earth's axis. When the Sun has covered exactly 15 degrees (1/24 of a circle, both angles being measured in a plane perpendicular to Earth's axis), local apparent time is 13:00 exactly; after 15 more degrees it will be 14:00 exactly. The problem is that in September the Sun takes less time (as me ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Longitude
Longitude (, ) is a geographic coordinate that specifies the east–west position of a point on the surface of the Earth, or another celestial body. It is an angular measurement, usually expressed in degrees and denoted by the Greek letter lambda (λ). Meridians are semicircular lines running from pole to pole that connect points with the same longitude. The prime meridian defines 0° longitude; by convention the International Reference Meridian for the Earth passes near the Royal Observatory in Greenwich, England on the island of Great Britain. Positive longitudes are east of the prime meridian, and negative ones are west. Because of the Earth's rotation, there is a close connection between longitude and time measurement. Scientifically precise local time varies with longitude: a difference of 15° longitude corresponds to a one-hour difference in local time, due to the differing position in relation to the Sun. Comparing local time to an absolute measure of time allows ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cylindrical Lens
A cylindrical lens is a lens which focuses light into a line instead of a point, as a spherical lens would. The curved face or faces of a cylindrical lens are sections of a cylinder, and focus the image passing through it into a line parallel to intersection of the surface of the lens and a plane tangent to it along the cylinder's axis. The lens converges or diverges the image in the direction perpendicular to this line, and leaves it unaltered in the direction parallel to its cylinder's axis (in the tangent plane). A toric lens combines the effect of a cylindrical lens with that of an ordinary spherical lens. Uses Uses in optometry * Cylindrical lenses are prescribed to correct astigmatism. * Cross cylinder, which is a combination of two cylindrical lenses with equal strength and opposite power, is used in subjective refraction to diagnose astigmatism, and assess the strength and axis of the astigmatic power etc. * Maddox rods, made up of cylindrical lenses arranged in parallel, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Greenwich
Greenwich ( , ,) is a town in south-east London, England, within the ceremonial county of Greater London. It is situated east-southeast of Charing Cross. Greenwich is notable for its maritime history and for giving its name to the Greenwich Meridian (0° longitude) and Greenwich Mean Time. The town became the site of a royal palace, the Palace of Placentia from the 15th century, and was the birthplace of many Tudors, including Henry VIII and Elizabeth I. The palace fell into disrepair during the English Civil War and was demolished to be replaced by the Royal Naval Hospital for Sailors, designed by Sir Christopher Wren and his assistant Nicholas Hawksmoor. These buildings became the Royal Naval College in 1873, and they remained a military education establishment until 1998 when they passed into the hands of the Greenwich Foundation. The historic rooms within these buildings remain open to the public; other buildings are used by University of Greenwich and Trinity Laban C ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
True North
True north (also called geodetic north or geographic north) is the direction along Earth's surface towards the geographic North Pole or True North Pole. Geodetic north differs from ''magnetic'' north (the direction a compass points toward the Magnetic North Pole), and from grid north (the direction northwards along the grid lines of a map projection). Geodetic true north also differs very slightly from ''astronomical'' true north (typically by a few arcseconds) because the local gravitational field may not point at the exact rotational axis of Earth. The direction of astronomical true north is marked in the skies by the north celestial pole. This is within about 1° of the position of Polaris, meaning the star would appear to trace a tiny circle in the sky each sidereal day. Due to the axial precession of Earth, true north rotates in an arc with respect to the stars that takes approximately 25,000 years to complete. Around 2101–2103, Polaris will make its closest approac ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
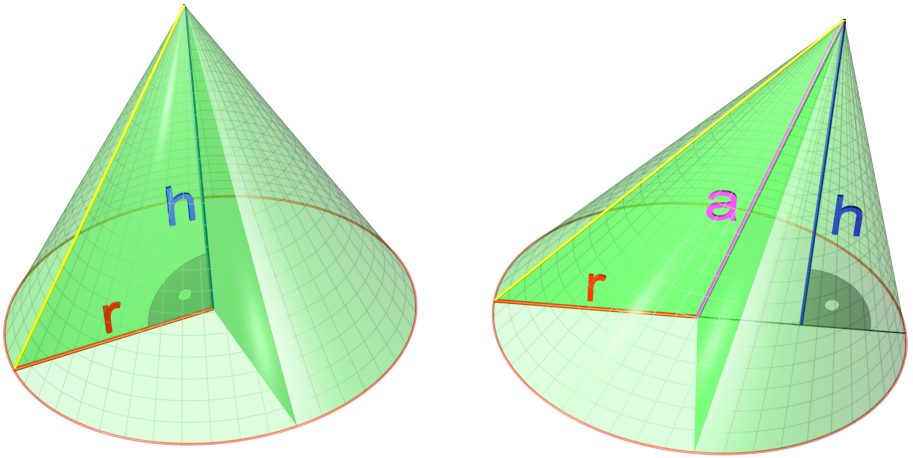
Cone (geometry)
A cone is a three-dimensional geometric shape that tapers smoothly from a flat base (frequently, though not necessarily, circular) to a point called the apex or vertex. A cone is formed by a set of line segments, half-lines, or lines connecting a common point, the apex, to all of the points on a base that is in a plane that does not contain the apex. Depending on the author, the base may be restricted to be a circle, any one-dimensional quadratic form in the plane, any closed one-dimensional figure, or any of the above plus all the enclosed points. If the enclosed points are included in the base, the cone is a solid object; otherwise it is a two-dimensional object in three-dimensional space. In the case of a solid object, the boundary formed by these lines or partial lines is called the ''lateral surface''; if the lateral surface is unbounded, it is a conical surface. In the case of line segments, the cone does not extend beyond the base, while in the case of half-lin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |



%2C_Phang_Nga_Bay%2C_Thailand.jpg)