|
Region (geometry)
In geography, regions, otherwise referred to as areas, zones, lands or territories, are portions of the Earth's surface that are broadly divided by physical characteristics (physical geography), human impact characteristics (human geography), and the interaction of humanity and the environment ( environmental geography). Geographic regions and sub-regions are mostly described by their imprecisely defined, and sometimes transitory boundaries, except in human geography, where jurisdiction areas such as national borders are defined in law. More confined or well bounded portions are called '' locations'' or ''places''. Apart from the global continental regions, there are also hydrospheric and atmospheric regions that cover the oceans, and discrete climates above the land and water masses of the planet. The land and water global regions are divided into subregions geographically bounded by large geological features that influence large-scale ecologies, such as plains and features. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Geography
Geography (from Ancient Greek ; combining 'Earth' and 'write', literally 'Earth writing') is the study of the lands, features, inhabitants, and phenomena of Earth. Geography is an all-encompassing discipline that seeks an understanding of Earth and world, its human and natural complexities—not merely where objects are, but also how they have changed and come to be. While geography is specific to Earth, many concepts can be applied more broadly to other Astronomical object, celestial bodies in the field of planetary science. Geography has been called "a bridge between natural science and social science disciplines." Origins of many of the concepts in geography can be traced to Greek Eratosthenes of Cyrene, who may have coined the term "geographia" (). The first recorded use of the word Geography (Ptolemy), γεωγραφία was as the title of a book by Greek scholar Claudius Ptolemy (100 – 170 AD). This work created the so-called "Ptolemaic tradition" of geography, w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Cultural Geography
Cultural geography is a subfield within human geography. Though the first traces of the study of different nations and cultures on Earth can be dated back to ancient geographers such as Ptolemy or Strabo, cultural geography as academic study firstly emerged as an alternative to the Environmental determinism, environmental determinist theories of the early 20th century, which had believed that people and societies are controlled by the Natural environment, environment in which they develop.Peet, Richard; 1990; Modern Geographical Thought; Blackwell Rather than studying predetermined regions based upon environmental classifications, cultural geography became interested in cultural landscapes. This was led by the "father of cultural geography" Carl O. Sauer of the University of California, Berkeley. As a result, cultural geography was long dominated by United States, American writers. Geographers drawing on this tradition see cultures and societies as developing out of their local l ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Physical World Map
Physical may refer to: *Physical examination, a regular overall check-up with a doctor *Physical (Olivia Newton-John album), ''Physical'' (Olivia Newton-John album), 1981 **Physical (Olivia Newton-John song), "Physical" (Olivia Newton-John song) *Physical (Gabe Gurnsey album), ''Physical'' (Gabe Gurnsey album) *Physical (Alcazar song), "Physical" (Alcazar song) (2004) *Physical (Enrique Iglesias song), "Physical" (Enrique Iglesias song) (2014) *Physical (Dua Lipa song), "Physical" (Dua Lipa song) (2020) *"Physical (You're So)", a 1980 song by Adam & the Ants, the B side to "Dog Eat Dog (Adam and the Ants song)#"Physical (You're So)", Dog Eat Dog" *Physical (TV series), ''Physical'' (TV series), an American television series *''Physical: 100'', a Korean reality show on Netflix See also {{disambiguation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Ethnography
Ethnography is a branch of anthropology and the systematic study of individual cultures. It explores cultural phenomena from the point of view of the subject of the study. Ethnography is also a type of social research that involves examining the behavior of the participants in a given social situation and understanding the group members' own interpretation of such behavior. As a form of inquiry, ethnography relies heavily on participant observation, where the researcher participates in the setting or with the people being studied, at least in some marginal role, and seeking to document, in detail, patterns of social interaction and the perspectives of participants, and to understand these in their local contexts. It had its origin in social and cultural anthropology in the early twentieth century, but has, since then, spread to other social science disciplines, notably sociology. Ethnographers mainly use Qualitative research, qualitative methods, though they may also include ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Soil Type
A soil type is a taxonomic unit in soil science. All soils that share a certain set of well-defined properties form a distinctive soil type. Soil type is a technical term of soil classification, the science that deals with the systematic categorization of soils. Every soil of the world belongs to a certain soil type. Soil type is an abstract term. In nature, you will not find soil types. You will find soils that belong to a certain soil type. In hierarchical soil classification systems, soil types mostly belong to the higher or intermediate level. A soil type can normally be subdivided into subtypes, and in many systems several soil types can be combined to entities of higher category. However, in the first classification system of the United States (Whitney, 1909), the soil type was the lowest level and the mapping unit. For the definition of soil types, some systems use primarily such characteristics that are the result of soil-forming processes ( pedogenesis). An example is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Mountain Range
A mountain range or hill range is a series of mountains or hills arranged in a line and connected by high ground. A mountain system or mountain belt is a group of mountain ranges with similarity in form, structure, and alignment that have arisen from the same cause, usually an orogeny. Mountain ranges are formed by a variety of geological processes, but most of the significant ones on Earth are the result of plate tectonics. Mountain ranges are also found on many planetary mass objects in the Solar System and are likely a feature of most terrestrial planets. Mountain ranges are usually segmented by highlands or mountain passes and valleys. Individual mountains within the same mountain range do not necessarily have the same geologic structure or petrology. They may be a mix of different orogenic expressions and terranes, for example thrust sheets, uplifted blocks, fold mountains, and volcanic landforms resulting in a variety of rock types. Major ranges Most geolo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Natural Region
A natural region (landscape unit) is a basic geographic unit. Usually, it is a region which is distinguished by its common natural features of geography, geology, and climate. From the ecological point of view, the naturally occurring flora and fauna of the region are likely to be influenced by its geographical and geological factors, such as soil and water availability, in a significant manner. Thus most natural regions are homogeneous ecosystems. Human impact can be an important factor in the shaping and destiny of a particular natural region. Main terms The concept "natural region" is a large basic geographical unit, like the vast boreal forest region. The term may also be used generically, like in alpine tundra, or specifically to refer to a particular place. The term is particularly useful where there is no corresponding or coterminous official region. The Fens of eastern England, the Thai highlands, and the Pays de Bray in Normandy, are examples of this. Others mig ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Drainage Basin
A drainage basin is an area of land in which all flowing surface water converges to a single point, such as a river mouth, or flows into another body of water, such as a lake or ocean. A basin is separated from adjacent basins by a perimeter, the drainage divide, made up of a succession of elevated features, such as ridges and hills. A basin may consist of smaller basins that merge at river confluences, forming a hierarchical pattern. Other terms for a drainage basin are catchment area, catchment basin, drainage area, river basin, water basin, and impluvium. In North America, they are commonly called a watershed, though in other English-speaking places, " watershed" is used only in its original sense, that of the drainage divide line. A drainage basin's boundaries are determined by watershed delineation, a common task in environmental engineering and science. In a closed drainage basin, or endorheic basin, rather than flowing to the ocean, water converges toward the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Biome
A biome () is a distinct geographical region with specific climate, vegetation, and animal life. It consists of a biological community that has formed in response to its physical environment and regional climate. In 1935, Tansley added the climatic and soil aspects to the idea, calling it ''ecosystem''. The International Biological Program (1964–74) projects popularized the concept of biome. However, in some contexts, the term ''biome'' is used in a different manner. In German literature, particularly in the Walter terminology, the term is used similarly as '' biotope'' (a concrete geographical unit), while the biome definition used in this article is used as an international, non-regional, terminology—irrespectively of the continent in which an area is present, it takes the same biome name—and corresponds to his "zonobiome", "orobiome" and "pedobiome" (biomes determined by climate zone, altitude or soil). In the Brazilian literature, the term ''biome'' is sometimes ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Biotope
A biotope is an area of uniform environmental conditions providing a living place for a specific assemblage of flora (plants), plants and fauna (animals), animals. ''Biotope'' is almost synonymous with the term habitat (ecology), "habitat", which is more commonly used in English-speaking countries. However, in some countries these two terms are distinguished: the subject of a habitat is a population, the subject of a biotope is a ''biocoenosis'' or "biological community". It is an English loanword derived from the German '':de:Biotop, Biotop'', which in turn came from the Greek ''bios'' (meaning 'life') and ''topos'' ('place'). (The related word ''geotope'' has made its way into the English language by the same route, from the German '':de:Geotop, Geotop''.) Ecology The concept of a biotope was first advocated by Ernst Haeckel (1834–1919), a German zoologist famous for the recapitulation theory. In his book ''General Morphology'' (1866), which defines the term "ecology", he st ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Ecosystem
An ecosystem (or ecological system) is a system formed by Organism, organisms in interaction with their Biophysical environment, environment. The Biotic material, biotic and abiotic components are linked together through nutrient cycles and energy flows. Ecosystems are controlled by external and internal Environmental factor, factors. External factors—including climate—control the ecosystem's structure, but are not influenced by it. By contrast, internal factors control and are controlled by ecosystem processes; these include decomposition, the types of species present, root competition, shading, disturbance, and succession. While external factors generally determine which Resource (biology), resource inputs an ecosystem has, their availability within the ecosystem is controlled by internal factors. Ecosystems are wikt:dynamic, dynamic, subject to periodic disturbances and always in the process of recovering from past disturbances. The tendency of an ecosystem to remain clo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
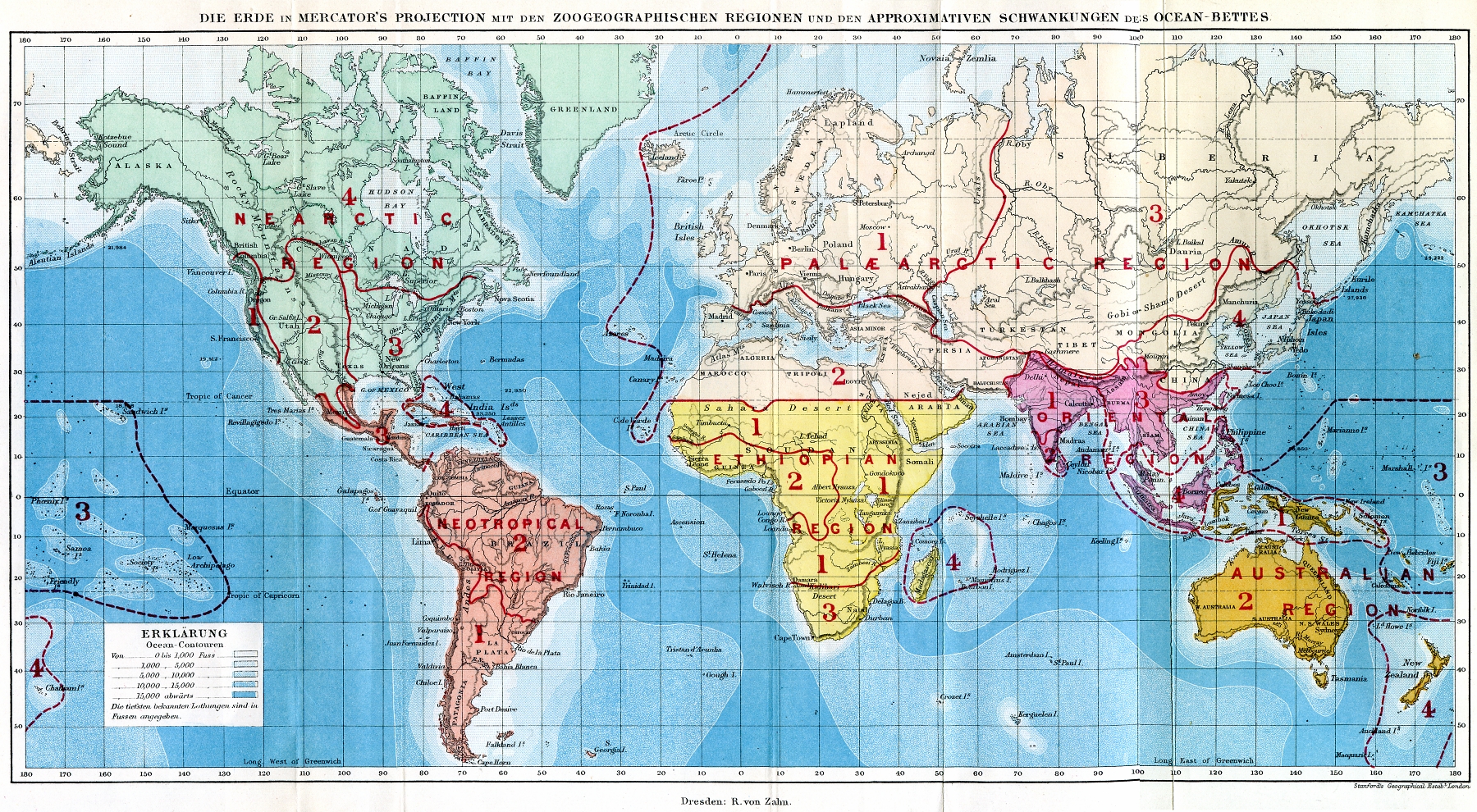
Zoogeography
Zoogeography is the branch of the science of biogeography that is concerned with geographic distribution (present and past) of animal species. As a multifaceted field of study, zoogeography incorporates methods of molecular biology, genetics, morphology, phylogenetics, and Geographic Information Systems (GIS) to delineate evolutionary events within defined regions of study around the globe. As proposed by Alfred Russel Wallace, known as the father of zoogeography, phylogenetic affinities can be quantified among zoogeographic regions, further elucidating the phenomena surrounding geographic distributions of organisms and explaining evolutionary relationships of taxa. Advancements in molecular biology and theory of evolution within zoological research has unraveled questions concerning speciation events and has expanded phylogenic relationships amongst taxa. Integration of phylogenetics with GIS provides a means for communicating evolutionary origins through cartographic design. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |