|
Recursive Grammar
In computer science, a grammar is informally called a recursive grammar if it contains production rules that are recursive, meaning that expanding a non-terminal according to these rules can eventually lead to a string that includes the same non-terminal again. Otherwise it is called a non-recursive grammar.. For example, a grammar for a context-free language is left recursive if there exists a non-terminal symbol ''A'' that can be put through the production rules to produce a string with ''A'' (as the leftmost symbol). All types of grammars in the Chomsky hierarchy can be recursive and it is recursion that allows the production of infinite sets of words. Properties A non-recursive grammar can produce only a finite language; and each finite language can be produced by a non-recursive grammar. For example, a straight-line grammar produces just a single word. A recursive context-free grammar that contains no useless rules necessarily produces an infinite language. This proper ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Computer Science
Computer science is the study of computation, information, and automation. Computer science spans Theoretical computer science, theoretical disciplines (such as algorithms, theory of computation, and information theory) to Applied science, applied disciplines (including the design and implementation of Computer architecture, hardware and Software engineering, software). Algorithms and data structures are central to computer science. The theory of computation concerns abstract models of computation and general classes of computational problem, problems that can be solved using them. The fields of cryptography and computer security involve studying the means for secure communication and preventing security vulnerabilities. Computer graphics (computer science), Computer graphics and computational geometry address the generation of images. Programming language theory considers different ways to describe computational processes, and database theory concerns the management of re ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Formal Grammar
A formal grammar is a set of Terminal and nonterminal symbols, symbols and the Production (computer science), production rules for rewriting some of them into every possible string of a formal language over an Alphabet (formal languages), alphabet. A grammar does not describe the semantics, meaning of the strings — only their form. In applied mathematics, formal language theory is the discipline that studies formal grammars and languages. Its applications are found in theoretical computer science, theoretical linguistics, Formal semantics (logic), formal semantics, mathematical logic, and other areas. A formal grammar is a Set_(mathematics), set of rules for rewriting strings, along with a "start symbol" from which rewriting starts. Therefore, a grammar is usually thought of as a language generator. However, it can also sometimes be used as the basis for a "recognizer"—a function in computing that determines whether a given string belongs to the language or is grammatical ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Recursion (computer Science)
In computer science, recursion is a method of solving a computational problem where the solution depends on solutions to smaller instances of the same problem. Recursion solves such recursion, recursive problems by using function (computer science), functions that call themselves from within their own code. The approach can be applied to many types of problems, and recursion is one of the central ideas of computer science. Most computer programming languages support recursion by allowing a function to call itself from within its own code. Some functional programming languages (for instance, Clojure) do not define any looping constructs but rely solely on recursion to repeatedly call code. It is proved in computability theory that these recursive-only languages are Turing complete; this means that they are as powerful (they can be used to solve the same problems) as imperative languages based on control structures such as and . Repeatedly calling a function from within itse ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Context-free Language
In formal language theory, a context-free language (CFL), also called a Chomsky type-2 language, is a language generated by a context-free grammar (CFG). Context-free languages have many applications in programming languages, in particular, most arithmetic expressions are generated by context-free grammars. Background Context-free grammar Different context-free grammars can generate the same context-free language. Intrinsic properties of the language can be distinguished from extrinsic properties of a particular grammar by comparing multiple grammars that describe the language. Automata The set of all context-free languages is identical to the set of languages accepted by pushdown automata, which makes these languages amenable to parsing. Further, for a given CFG, there is a direct way to produce a pushdown automaton for the grammar (and thereby the corresponding language), though going the other way (producing a grammar given an automaton) is not as direct. Examples An e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
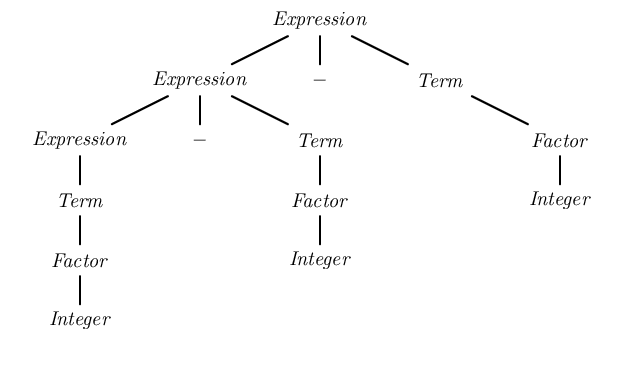
Left Recursion
In the formal language theory of computer science, left recursion is a special case of recursion where a string is recognized as part of a language by the fact that it decomposes into a string from that same language (on the left) and a suffix (on the right). For instance, 1+2+3 can be recognized as a sum because it can be broken into 1+2, also a sum, and +3, a suitable suffix. In terms of context-free grammar, a nonterminal is left-recursive if the leftmost symbol in one of its productions is itself (in the case of direct left recursion) or can be made itself by some sequence of substitutions (in the case of indirect left recursion). Definition A grammar is left-recursive if and only if there exists a nonterminal symbol A that can derive to a sentential form with itself as the leftmost symbol.. James Power, Department of Computer Science National University of Ireland, Maynooth Maynooth, Co. Kildare, Ireland. JPR02 Symbolically, : A \Rightarrow^+ A\alpha, where \Rightarrow^+ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Chomsky Hierarchy
The Chomsky hierarchy in the fields of formal language theory, computer science, and linguistics, is a containment hierarchy of classes of formal grammars. A formal grammar describes how to form strings from a formal language's alphabet that are valid according to the language's syntax. The linguist Noam Chomsky theorized that four different classes of formal grammars existed that could generate increasingly complex languages. Each class can also completely generate the language of all inferior classes (set inclusive). History The general idea of a hierarchy of grammars was first described by Noam Chomsky in "Three models for the description of language" during the formalization of transformational-generative grammar (TGG). Marcel-Paul Schützenberger also played a role in the development of the theory of formal languages; the paper "The algebraic theory of context free languages" describes the modern hierarchy, including context-free grammars. Independently, alongside linguis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Straight-line Grammar
A straight-line grammar (sometimes abbreviated as SLG) is a formal grammar that generates exactly one string.Florian Benz and Timo Kötzing, “An effective heuristic for the smallest grammar problem,” Proceedings of the fifteenth annual conference on Genetic and evolutionary computation conference - GECCO ’13, 2013. , p. 488 Consequently, it does not branch (every non-terminal has only one associated production rule) nor loop (if non-terminal ''A'' appears in a derivation of ''B'', then ''B'' does not appear in a derivation of ''A''). Areas of usefulness Straight-line grammars are widely used in the development of algorithms that execute directly on compressed structures (without prior decompression). SLGs are of interest in fields like Kolmogorov complexity, Lossless data compression, Structure discovery and Compressed data structures. The problem of finding a context-free grammar (equivalently: an SLG) of minimal size that generates a given string is called the smal ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Useless Rules
In formal language theory, a context-free grammar (CFG) is a formal grammar whose production rules can be applied to a nonterminal symbol regardless of its context. In particular, in a context-free grammar, each production rule is of the form : A\ \to\ \alpha with A a ''single'' nonterminal symbol, and \alpha a string of terminals and/or nonterminals (\alpha can be empty). Regardless of which symbols surround it, the single nonterminal A on the left hand side can always be replaced by \alpha on the right hand side. This distinguishes it from a context-sensitive grammar, which can have production rules in the form \alpha A \beta \rightarrow \alpha \gamma \beta with A a nonterminal symbol and \alpha, \beta, and \gamma strings of terminal and/or nonterminal symbols. A formal grammar is essentially a set of production rules that describe all possible strings in a given formal language. Production rules are simple replacements. For example, the first rule in the picture, : \langle ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Algorithm
In mathematics and computer science, an algorithm () is a finite sequence of Rigour#Mathematics, mathematically rigorous instructions, typically used to solve a class of specific Computational problem, problems or to perform a computation. Algorithms are used as specifications for performing calculations and data processing. More advanced algorithms can use Conditional (computer programming), conditionals to divert the code execution through various routes (referred to as automated decision-making) and deduce valid inferences (referred to as automated reasoning). In contrast, a Heuristic (computer science), heuristic is an approach to solving problems without well-defined correct or optimal results.David A. Grossman, Ophir Frieder, ''Information Retrieval: Algorithms and Heuristics'', 2nd edition, 2004, For example, although social media recommender systems are commonly called "algorithms", they actually rely on heuristics as there is no truly "correct" recommendation. As an e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |