|
Periapsis
An apsis (; ) is the farthest or nearest point in the orbit of a planetary body about its primary (astronomy), primary body. For example, the apsides of the Earth are called the aphelion and perihelion. General description There are two apsides in any elliptic orbit. The name for each apsis is created from the prefixes ''ap-'', ''apo-'' (), or ''peri-'' (), each referring to the farthest and closest point to the primary body the affixing necessary suffix that describes the primary body in the orbit. In this case, the suffix for Earth is ''-gee'', so the apsides' names are ''apogee'' and ''perigee''. For the Sun, its suffix is ''-helion'', so the names are ''aphelion'' and ''perihelion''. According to Newton's laws of motion, all periodic orbits are ellipses. The barycenter of the two bodies may lie well within the bigger body—e.g., the Earth–Moon barycenter is about 75% of the way from Earth's center to its surface. If, compared to the larger mass, the smaller mass i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Apogee (PSF)
An apsis (; ) is the farthest or nearest point in the orbit of a planetary body about its primary (astronomy), primary body. For example, the apsides of the Earth are called the aphelion and perihelion. General description There are two apsides in any elliptic orbit. The name for each apsis is created from the prefixes ''ap-'', ''apo-'' (), or ''peri-'' (), each referring to the farthest and closest point to the primary body the affixing necessary suffix that describes the primary body in the orbit. In this case, the suffix for Earth is ''-gee'', so the apsides' names are ''apogee'' and ''perigee''. For the Sun, its suffix is ''-helion'', so the names are ''aphelion'' and ''perihelion''. According to Newton's laws of motion, all periodic orbits are ellipses. The barycenter of the two bodies may lie well within the bigger body—e.g., the Earth–Moon barycenter is about 75% of the way from Earth's center to its surface. If, compared to the larger mass, the smaller mass i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Periapsis Apoapsis
An apsis (; ) is the farthest or nearest point in the orbit of a planetary body about its primary body. For example, the apsides of the Earth are called the aphelion and perihelion. General description There are two apsides in any elliptic orbit. The name for each apsis is created from the prefixes ''ap-'', ''apo-'' (), or ''peri-'' (), each referring to the farthest and closest point to the primary body the affixing necessary suffix that describes the primary body in the orbit. In this case, the suffix for Earth is ''-gee'', so the apsides' names are ''apogee'' and ''perigee''. For the Sun, its suffix is ''-helion'', so the names are ''aphelion'' and ''perihelion''. According to Newton's laws of motion, all periodic orbits are ellipses. The barycenter of the two bodies may lie well within the bigger body—e.g., the Earth–Moon barycenter is about 75% of the way from Earth's center to its surface. If, compared to the larger mass, the smaller mass is negligible (e.g., f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mars
Mars is the fourth planet from the Sun and the second-smallest planet in the Solar System, only being larger than Mercury (planet), Mercury. In the English language, Mars is named for the Mars (mythology), Roman god of war. Mars is a terrestrial planet with a thin atmosphere (less than 1% that of Earth's), and has a crust primarily composed of elements similar to Earth's crust, as well as a core made of iron and nickel. Mars has surface features such as impact craters, valleys, dunes and polar ice caps. It has two small and irregularly shaped moons, Phobos (moon), Phobos and Deimos (moon), Deimos. Some of the most notable surface features on Mars include Olympus Mons, the largest volcano and List of tallest mountains in the Solar System, highest known mountain in the Solar System and Valles Marineris, one of the largest canyons in the Solar System. The North Polar Basin (Mars), Borealis basin in the Northern Hemisphere covers approximately 40% of the planet and may be a la ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Venus
Venus is the second planet from the Sun. It is sometimes called Earth's "sister" or "twin" planet as it is almost as large and has a similar composition. As an interior planet to Earth, Venus (like Mercury) appears in Earth's sky never far from the Sun, either as morning star or evening star. Aside from the Sun and Moon, Venus is the brightest natural object in Earth's sky, capable of casting visible shadows on Earth at dark conditions and being visible to the naked eye in broad daylight. Venus is the second largest terrestrial object of the Solar System. It has a surface gravity slightly lower than on Earth and has a very weak induced magnetosphere. The atmosphere of Venus, mainly consists of carbon dioxide, and is the densest and hottest of the four terrestrial planets at the surface. With an atmospheric pressure at the planet's surface of about 92 times the sea level pressure of Earth and a mean temperature of , the carbon dioxide gas at Venus's surface is in the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mercury (planet)
Mercury is the smallest planet in the Solar System and the closest to the Sun. Its orbit around the Sun takes 87.97 Earth days, the shortest of all the Sun's planets. It is named after the Roman god ' ( Mercury), god of commerce, messenger of the gods, and mediator between gods and mortals, corresponding to the Greek god Hermes (). Like Venus, Mercury orbits the Sun within Earth's orbit as an inferior planet, and its apparent distance from the Sun as viewed from Earth never exceeds 28°. This proximity to the Sun means the planet can only be seen near the western horizon after sunset or the eastern horizon before sunrise, usually in twilight. At this time, it may appear as a bright star-like object, but is more difficult to observe than Venus. From Earth, the planet telescopically displays the complete range of phases, similar to Venus and the Moon, which recurs over its synodic period of approximately 116 days. The synodic proximity of Mercury to Earth makes Mercury most ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Astronomical Object
An astronomical object, celestial object, stellar object or heavenly body is a naturally occurring physical entity, association, or structure that exists in the observable universe. In astronomy, the terms ''object'' and ''body'' are often used interchangeably. However, an astronomical body or celestial body is a single, tightly bound, contiguous entity, while an astronomical or celestial ''object'' is a complex, less cohesively bound structure, which may consist of multiple bodies or even other objects with substructures. Examples of astronomical objects include planetary systems, star clusters, nebulae, and galaxies, while asteroids, moons, planets, and stars are astronomical bodies. A comet may be identified as both body and object: It is a ''body'' when referring to the frozen nucleus of ice and dust, and an ''object'' when describing the entire comet with its diffuse coma and tail. History Astronomical objects such as stars, planets, nebulae, asteroids and comets ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Exoplanet
An exoplanet or extrasolar planet is a planet outside the Solar System. The first possible evidence of an exoplanet was noted in 1917 but was not recognized as such. The first confirmation of detection occurred in 1992. A different planet, initially detected in 1988, was confirmed in 2003. There are many methods of detecting exoplanets. Transit photometry and Doppler spectroscopy have found the most, but these methods suffer from a clear observational bias favoring the detection of planets near the star; thus, 85% of the exoplanets detected are inside the tidal locking zone. In several cases, multiple planets have been observed around a star. About 1 in 5 Sun-like starsFor the purpose of this 1 in 5 statistic, "Sun-like" means G-type star. Data for Sun-like stars was not available so this statistic is an extrapolation from data about K-type stars. have an "Earth-sized"For the purpose of this 1 in 5 statistic, Earth-sized means 1–2 Earth radii. planet in the habitable zone. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bothros
Bothros (Greek βόθρος, plural ''bothroi'') is the Ancient Greek word for "hole", "pit" or "trench". In contemporary use it can refer to a variety of holes or depressions found at ancient sites and referred to in literature, and has also been utilized in biological taxonomy to describe species or structures that have similar characteristics. Historic / Archaeological uses In Greek antiquity, a ''bothros'' was an artificially-created or formed depression in the ground, which could serve various purposes. In archaeology, similar items are also referred to by this name and interpreted depending on their context as altars, locations for sacrifice or storage pits. In the works of Homer, ''bothros'' generally refers to a depression or pit in the ground. In the Odyssey, the handmaidens of Nausicaa wash their clothes in one, and at the advice of Circe Odysseus digs one for the offering of libations to the dead in the underworld - first honey and milk, then wine, then water. They we ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Infinity Plus
''Infinity Plus'' (sometimes stylized as ''infinity plus'' and ''infinityplus'') was a science fiction webzine active from 1997 to 2007,science fiction, fantasy and horror from infinity plus retrieved May 13, 2018 specializing in reviews, interviews, and professionally written fiction. It was founded by (who took a "deliberately elitist approach"); The story of infinity plus originally published in '' Interzone ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Asimov's Science Fiction
''Asimov's Science Fiction'' is an American science fiction magazine which publishes science fiction and fantasy named after science fiction author Isaac Asimov. It is currently published by Penny Publications. From January 2017, the publication frequency is bimonthly (six issues per year). Circulation in 2012 was 22,593, as reported in the annual ''Locus Magazine survey. History ''Asimov's Science Fiction'' began life as the digest-sized ''Isaac Asimov's Science Fiction Magazine'' (or ''IASFM'' for short) in 1977. Joel Davis of Davis Publications approached Asimov to lend his name to a new science fiction magazine, after the fashion of ''Ellery Queen's Mystery Magazine'' or ''Alfred Hitchcock's Mystery Magazine''. Asimov refused to act as editor, but served instead as editorial director, writing editorials and replying to reader mail until his death in 1992. At Asimov's request George Scithers, the first editor, negotiated an acquisitions contract with the Science Fiction Writ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geoffrey A
Geoffrey, Geoffroy, Geoff, etc., may refer to: People * Geoffrey (name), including a list of people with the name * Geoffroy (surname), including a list of people with the name * Geoffrey of Monmouth (c. 1095–c. 1155), clergyman and one of the major figures in the development of British history * Geoffrey I of Anjou (died 987) * Geoffrey II of Anjou (died 1060) * Geoffrey III of Anjou (died 1096) * Geoffrey IV of Anjou (died 1106) * Geoffrey V, Count of Anjou (1113–1151), father of King Henry II of England * Geoffrey II, Duke of Brittany (1158–1186), one of Henry II's sons * Geoffrey, Archbishop of York (c. 1152–1212) * Geoffroy du Breuil of Vigeois, 12th century French chronicler * Geoffroy de Charney (died 1314), Preceptor of the Knights Templar * Geoffroy IV de la Tour Landry (c. 1320–1391), French nobleman and writer * Geoffrey the Baker (died c. 1360), English historian and chronicler * Geoffroy (musician) (born 1987), Canadian singer, songwriter and multi-instrum ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
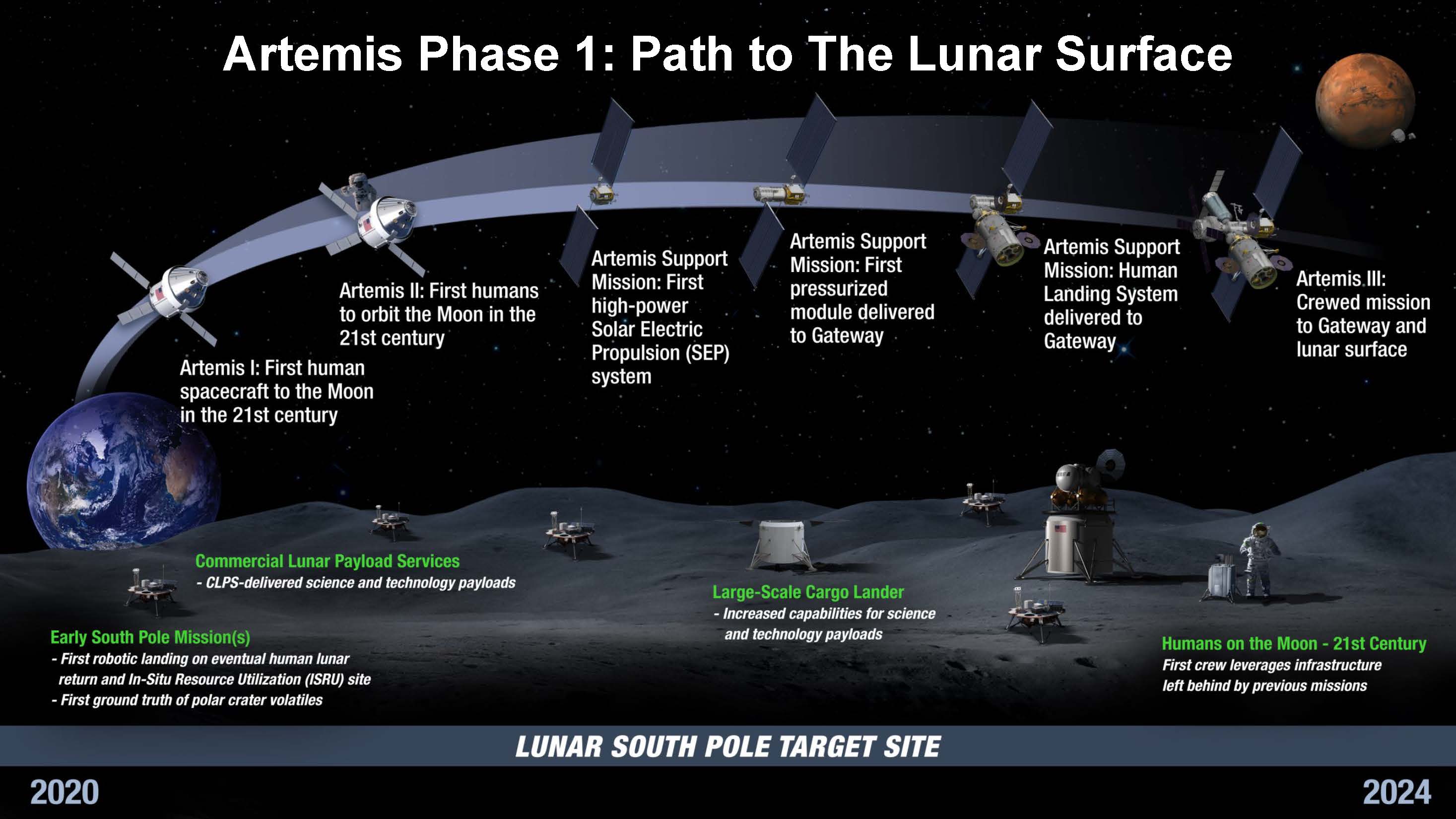
Artemis Program
The Artemis program is a robotic and human Moon exploration program led by the United States' National Aeronautics and Space Administration (NASA) along with three partner agencies: European Space Agency (ESA), Japan Aerospace Exploration Agency (JAXA), and Canadian Space Agency (CSA). The Artemis program intends to reestablish a human presence on the Moon for the first time since the Apollo 17 mission in 1972. The major components of the program are the Space Launch System (SLS), Orion spacecraft, Lunar Gateway space station and the commercial Human Landing Systems. The program's long-term goal is to establish a permanent base camp on the Moon and facilitate human missions to Mars. The Artemis program is a collaboration of government space agencies and private spaceflight companies, bound together by the Artemis Accords and supporting contracts. As of July 2022, twenty-one countries have signed the accords, including traditional U.S. space partners (such as the Euro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
.png)