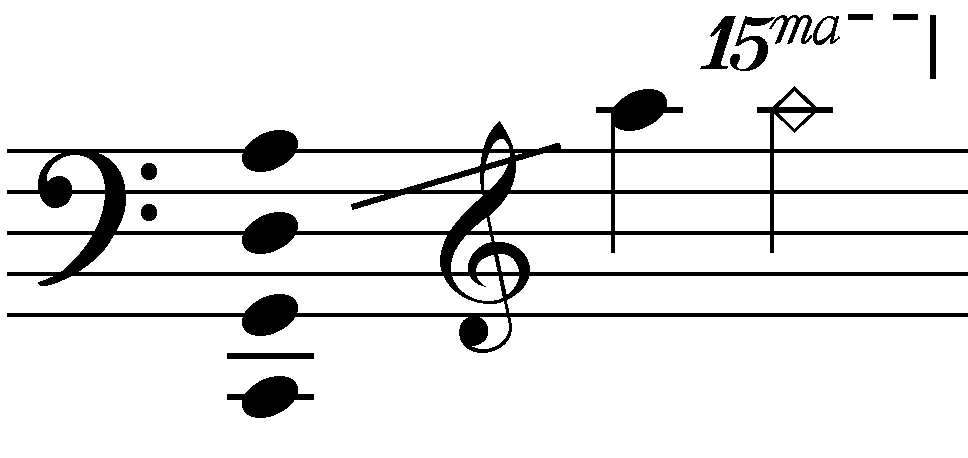|
Harmonic
A harmonic is a wave with a frequency that is a positive integer multiple of the ''fundamental frequency'', the frequency of the original periodic signal, such as a sinusoidal wave. The original signal is also called the ''1st harmonic'', the other harmonics are known as ''higher harmonics''. As all harmonics are periodic at the fundamental frequency, the sum of harmonics is also periodic at that frequency. The set of harmonics forms a '' harmonic series''. The term is employed in various disciplines, including music, physics, acoustics, electronic power transmission, radio technology, and other fields. For example, if the fundamental frequency is 50 Hz, a common AC power supply frequency, the frequencies of the first three higher harmonics are 100 Hz (2nd harmonic), 150 Hz (3rd harmonic), 200 Hz (4th harmonic) and any addition of waves with these frequencies is periodic at 50 Hz. In music, harmonics are used on string instruments and wind ins ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Harmonic Series (music)
A harmonic series (also overtone series) is the sequence of harmonics, musical tones, or pure tones whose frequency is an integer multiple of a ''fundamental frequency''. Pitched musical instruments are often based on an acoustic resonator such as a string or a column of air, which oscillates at numerous modes simultaneously. At the frequencies of each vibrating mode, waves travel in both directions along the string or air column, reinforcing and canceling each other to form standing waves. Interaction with the surrounding air causes audible sound waves, which travel away from the instrument. Because of the typical spacing of the resonances, these frequencies are mostly limited to integer multiples, or harmonics, of the lowest frequency, and such multiples form the harmonic series. The musical pitch of a note is usually perceived as the lowest partial present (the fundamental frequency), which may be the one created by vibration over the full length of the string or air c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Consonance
In music, consonance and dissonance are categorizations of simultaneous or successive sounds. Within the Western tradition, some listeners associate consonance with sweetness, pleasantness, and acceptability, and dissonance with harshness, unpleasantness, or unacceptability, although there is broad acknowledgement that this depends also on familiarity and musical expertise. The terms form a structural dichotomy in which they define each other by mutual exclusion: a consonance is what is not dissonant, and a dissonance is what is not consonant. However, a finer consideration shows that the distinction forms a gradation, from the most consonant to the most dissonant. In casual discourse, as German composer and music theorist Paul Hindemith stressed, "The two concepts have never been completely explained, and for a thousand years the definitions have varied". The term ''sonance'' has been proposed to encompass or refer indistinctly to the terms ''consonance'' and ''dissonance''. De ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Violin
The violin, sometimes known as a '' fiddle'', is a wooden chordophone ( string instrument) in the violin family. Most violins have a hollow wooden body. It is the smallest and thus highest-pitched instrument ( soprano) in the family in regular use. The violin typically has four strings (some can have five), usually tuned in perfect fifths with notes G3, D4, A4, E5, and is most commonly played by drawing a bow across its strings. It can also be played by plucking the strings with the fingers (pizzicato) and, in specialized cases, by striking the strings with the wooden side of the bow (col legno). Violins are important instruments in a wide variety of musical genres. They are most prominent in the Western classical tradition, both in ensembles (from chamber music to orchestras) and as solo instruments. Violins are also important in many varieties of folk music, including country music, bluegrass music, and in jazz. Electric violins with solid bodies and piezoelectri ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Timbre
In music, timbre ( ), also known as tone color or tone quality (from psychoacoustics), is the perceived sound quality of a musical note, sound or tone. Timbre distinguishes different types of sound production, such as choir voices and musical instruments. It also enables listeners to distinguish different instruments in the same category (e.g., an oboe and a clarinet, both woodwind instruments). In simple terms, timbre is what makes a particular musical instrument or human voice have a different sound from another, even when they play or sing the same note. For instance, it is the difference in sound between a guitar and a piano playing the same note at the same volume. Both instruments can sound equally tuned in relation to each other as they play the same note, and while playing at the same amplitude level each instrument will still sound distinctively with its own unique tone color. Experienced musicians are able to distinguish between different instruments of the same typ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fundamental Frequency
The fundamental frequency, often referred to simply as the ''fundamental'', is defined as the lowest frequency of a periodic waveform. In music, the fundamental is the musical pitch of a note that is perceived as the lowest partial present. In terms of a superposition of sinusoids, the fundamental frequency is the lowest frequency sinusoidal in the sum of harmonically related frequencies, or the frequency of the difference between adjacent frequencies. In some contexts, the fundamental is usually abbreviated as 0, indicating the lowest frequency counting from zero. In other contexts, it is more common to abbreviate it as 1, the first harmonic. (The second harmonic is then 2 = 2⋅1, etc. In this context, the zeroth harmonic would be 0 Hz.) According to Benward's and Saker's ''Music: In Theory and Practice'': Explanation All sinusoidal and many non-sinusoidal waveforms repeat exactly over time – they are periodic. The period of a waveform is the smallest value of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dynamic Tonality
Dynamic tonality is a paradigm for tuning and timbre which generalizes the special relationship between just intonation and the harmonic series to apply to a wider set of pseudo-just tunings and related pseudo-harmonic timbres.Duffin, R.W., 2006''How Equal Temperament Ruined Harmony (and Why You Should Care)''/ref> This misalignment, in any tuning that is not fully Just (and hence infinitely complex), is the defining characteristic of the Static Timbre Paradigm. Instruments Many of the pseudo-just temperaments proposed during this "temperament battle" were rank-2 (two-dimensional)—such as quarter-comma meantone—that provided more than 12 notes per octave. However, the standard piano-like keyboard is only rank-1 (one-dimensional), affording at most 12 notes per octave. Piano-like keyboards affording more than 12 notes per octave were developed by Vicentino, Colonna, Mersenne, Huygens, and Newton, but were deemed cumbersome and difficult to learn. The dynamic tonality parad ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Oscillator
Oscillation is the repetitive or periodic variation, typically in time, of some measure about a central value (often a point of equilibrium) or between two or more different states. Familiar examples of oscillation include a swinging pendulum and alternating current. Oscillations can be used in physics to approximate complex interactions, such as those between atoms. Oscillations occur not only in mechanical systems but also in dynamic systems in virtually every area of science: for example the beating of the human heart (for circulation), business cycles in economics, predator–prey population cycles in ecology, geothermal geysers in geology, vibration of strings in guitar and other string instruments, periodic firing of nerve cells in the brain, and the periodic swelling of Cepheid variable stars in astronomy. The term ''vibration'' is precisely used to describe a mechanical oscillation. Oscillation, especially rapid oscillation, may be an undesirable phenomenon in p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inharmonicity
In music, inharmonicity is the degree to which the frequencies of overtones (also known as partials or partial tones) depart from whole multiples of the fundamental frequency ( harmonic series). Acoustically, a note perceived to have a single distinct pitch in fact contains a variety of additional overtones. Many percussion instruments, such as cymbals, tam-tams, and chimes, create complex and inharmonic sounds. Music harmony and intonation depends strongly on the harmonicity of tones. An ideal, homogeneous, infinitesimally thin or infinitely flexible string or column of air has exactly harmonic modes of vibration. In any real musical instrument, the resonant body that produces the music tone—typically a string, wire, or column of air—deviates from this ideal and has some small or large amount of inharmonicity. For instance, a very thick string behaves less as an ideal string and more like a cylinder (a tube of mass), which has natural resonances that are not whole num ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sinusoidal Wave
A sine wave, sinusoidal wave, or just sinusoid is a mathematical curve defined in terms of the ''sine'' trigonometric function, of which it is the graph. It is a type of continuous wave and also a smooth periodic function. It occurs often in mathematics, as well as in physics, engineering, signal processing and many other fields. Formulation Its most basic form as a function of time (''t'') is: y(t) = A\sin(2 \pi f t + \varphi) = A\sin(\omega t + \varphi) where: * ''A'', ''amplitude'', the peak deviation of the function from zero. * ''f'', ''ordinary frequency'', the ''number'' of oscillations (cycles) that occur each second of time. * ''ω'' = 2''f'', ''angular frequency'', the rate of change of the function argument in units of radians per second. * \varphi, '' phase'', specifies (in radians) where in its cycle the oscillation is at ''t'' = 0. When \varphi is non-zero, the entire waveform appears to be shifted in time by the amount ''φ''/''ω'' seconds. A negative value rep ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cello Natural Harmonics
The cello ( ; plural ''celli'' or ''cellos'') or violoncello ( ; ) is a bowed (sometimes plucked and occasionally hit) string instrument of the violin family. Its four strings are usually tuned in perfect fifths: from low to high, C2, G2, D3 and A3. The viola's four strings are each an octave higher. Music for the cello is generally written in the bass clef, with tenor clef, and treble clef used for higher-range passages. Played by a ''cellist'' or ''violoncellist'', it enjoys a large solo repertoire with and without accompaniment, as well as numerous concerti. As a solo instrument, the cello uses its whole range, from bass to soprano, and in chamber music such as string quartets and the orchestra's string section, it often plays the bass part, where it may be reinforced an octave lower by the double basses. Figured bass music of the Baroque-era typically assumes a cello, viola da gamba or bassoon as part of the basso continuo group alongside chordal instruments such as o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multiphonics
A multiphonic is an extended technique on a monophonic musical instrument (one that generally produces only one note at a time) in which several notes are produced at once. This includes wind, reed, and brass instruments, as well as the human voice. Multiphonic-like sounds on string instruments, both bowed and hammered, have also been called multiphonics, for lack of better terminology and scarcity of research. Multiphonics on wind instruments are primarily a 20th-century technique, though the brass technique of singing while playing has been known since the 18th century and used by composers such as Carl Maria von Weber. Commonly, no more than four notes will be produced at once, though for some chords on some instruments it is possible to get several more. Technique Woodwind instruments On woodwind instruments—e.g., saxophone, clarinet, oboe, bassoon, flute, and recorder—multiphonics can be produced either with new fingerings, by using different embouchures, or voicing ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Alternating Current
Alternating current (AC) is an electric current which periodically reverses direction and changes its magnitude continuously with time in contrast to direct current (DC) which flows only in one direction. Alternating current is the form in which electric power is delivered to businesses and residences, and it is the form of electrical energy that consumers typically use when they plug kitchen appliances, televisions, fans and electric lamps into a wall socket. A common source of DC power is a battery cell in a flashlight. The abbreviations ''AC'' and ''DC'' are often used to mean simply ''alternating'' and ''direct'', as when they modify '' current'' or '' voltage''. The usual waveform of alternating current in most electric power circuits is a sine wave, whose positive half-period corresponds with positive direction of the current and vice versa. In certain applications, like guitar amplifiers, different waveforms are used, such as triangular waves or square waves. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
.jpg "Click for more on -> Timbre")
