|
Fluid Mechanics
Fluid mechanics is the branch of physics concerned with the mechanics of fluids ( liquids, gases, and plasmas) and the forces on them. It has applications in a wide range of disciplines, including mechanical, aerospace, civil, chemical and biomedical engineering, geophysics, oceanography, meteorology, astrophysics, and biology. It can be divided into fluid statics, the study of fluids at rest; and fluid dynamics, the study of the effect of forces on fluid motion. It is a branch of continuum mechanics, a subject which models matter without using the information that it is made out of atoms; that is, it models matter from a ''macroscopic'' viewpoint rather than from ''microscopic''. Fluid mechanics, especially fluid dynamics, is an active field of research, typically mathematically complex. Many problems are partly or wholly unsolved and are best addressed by numerical methods, typically using computers. A modern discipline, called computational fluid dynamics (CFD), is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Physics
Physics is the natural science that studies matter, its fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge which relates to the order of nature, or, in other words, to the regular succession of events." Physics is one of the most fundamental scientific disciplines, with its main goal being to understand how the universe behaves. "Physics is one of the most fundamental of the sciences. Scientists of all disciplines use the ideas of physics, including chemists who study the structure of molecules, paleontologists who try to reconstruct how dinosaurs walked, and climatologists who study how human activities affect the atmosphere and oceans. Physics is also the foundation of all engineering and technology. No engineer could design a flat-screen TV, an interplanetary spacecraft, or even a better mousetrap without first understanding the basic laws of phys ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fluid Dynamics
In physics and engineering, fluid dynamics is a subdiscipline of fluid mechanics that describes the flow of fluids— liquids and gases. It has several subdisciplines, including ''aerodynamics'' (the study of air and other gases in motion) and hydrodynamics (the study of liquids in motion). Fluid dynamics has a wide range of applications, including calculating forces and moments on aircraft, determining the mass flow rate of petroleum through pipelines, predicting weather patterns, understanding nebulae in interstellar space and modelling fission weapon detonation. Fluid dynamics offers a systematic structure—which underlies these practical disciplines—that embraces empirical and semi-empirical laws derived from flow measurement and used to solve practical problems. The solution to a fluid dynamics problem typically involves the calculation of various properties of the fluid, such as flow velocity, pressure, density, and temperature, as functions of space and ti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isaac Newton
Sir Isaac Newton (25 December 1642 – 20 March 1726/27) was an English mathematician, physicist, astronomer, alchemist, Theology, theologian, and author (described in his time as a "natural philosophy, natural philosopher"), widely recognised as one of the greatest mathematicians and physicists and among the most influential scientists of all time. He was a key figure in the philosophical revolution known as the Age of Enlightenment, Enlightenment. His book (''Mathematical Principles of Natural Philosophy''), first published in 1687, established classical mechanics. Newton also made seminal contributions to optics, and Multiple discovery, shares credit with German mathematician Gottfried Wilhelm Leibniz for developing calculus, infinitesimal calculus. In the , Newton formulated the Newton's laws of motion, laws of motion and Newton's law of universal gravitation, universal gravitation that formed the dominant scientific viewpoint for centuries until it was supersede ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Barometer
A barometer is a scientific instrument that is used to measure air pressure in a certain environment. Pressure tendency can forecast short term changes in the weather. Many measurements of air pressure are used within surface weather analysis to help find surface troughs, pressure systems and frontal boundaries. Barometers and pressure altimeters (the most basic and common type of altimeter) are essentially the same instrument, but used for different purposes. An altimeter is intended to be used at different levels matching the corresponding atmospheric pressure to the altitude, while a barometer is kept at the same level and measures subtle pressure changes caused by weather and elements of weather. The average atmospheric pressure on the earth's surface varies between 940 and 1040 hPa (mbar). The average atmospheric pressure at sea level is 1013 hPa (mbar). Etymology The word '' barometer'' is derived from the Ancient Greek (), meaning "weight", and (), meaning "me ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Evangelista Torricelli
Evangelista Torricelli ( , also , ; 15 October 160825 October 1647) was an Italian physicist and mathematician, and a student of Galileo. He is best known for his invention of the barometer, but is also known for his advances in optics and work on the method of indivisibles. The Torr is also named after him. Biography Early life Torricelli was born on 15 October 1608 in Rome, the firstborn child of Gaspare Torricelli and Caterina Angetti. His family was from Faenza in the Province of Ravenna, then part of the Papal States. His father was a textile worker and the family was very poor. Seeing his talents, his parents sent him to be educated in Faenza, under the care of his uncle, Giacomo (James), a Camaldolese monk, who first ensured that his nephew was given a sound basic education. He then entered young Torricelli into a Jesuit College in 1624, possibly the one in Faenza itself, to study mathematics and philosophy until 1626, by which time his father, Gaspare, had die ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Leonardo Da Vinci
Leonardo di ser Piero da Vinci (15 April 14522 May 1519) was an Italian polymath of the High Renaissance who was active as a painter, draughtsman, engineer, scientist, theorist, sculptor, and architect. While his fame initially rested on his achievements as a painter, he also became known for his notebooks, in which he made drawings and notes on a variety of subjects, including anatomy, astronomy, botany, cartography, painting, and paleontology. Leonardo is widely regarded to have been a genius who epitomized the Renaissance humanist ideal, and his collective works comprise a contribution to later generations of artists matched only by that of his younger contemporary, Michelangelo. Born out of wedlock to a successful notary and a lower-class woman in, or near, Vinci, he was educated in Florence by the Italian painter and sculptor Andrea del Verrocchio. He began his career in the city, but then spent much time in the service of Ludovico Sforza in Milan. Later, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
On Floating Bodies
''On Floating Bodies'' ( el, Περὶ τῶν ἐπιπλεόντων σωμάτων) is a Greek-language work consisting of two books written by Archimedes of Syracuse (287 – c. 212 BC), one of the most important mathematicians, physicists, and engineers of antiquity. ''On Floating Bodies'', which is thought to have been written around 250 BC, survives only partly in Greek, the rest in medieval Latin translation from the Greek. It is the first known work on hydrostatics, of which Archimedes is recognized as the founder. The purpose of ''On Floating Bodies'' was to determine the positions that various solids will assume when floating in a fluid, according to their form and the variation in their specific gravities. It contains the first statement of what is now known as Archimedes' principle. Overview Archimedes lived in the Greek city-state of Syracuse, Sicily. He is credited with laying the foundations of hydrostatics (which he established in ''On Floating Bodies'' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
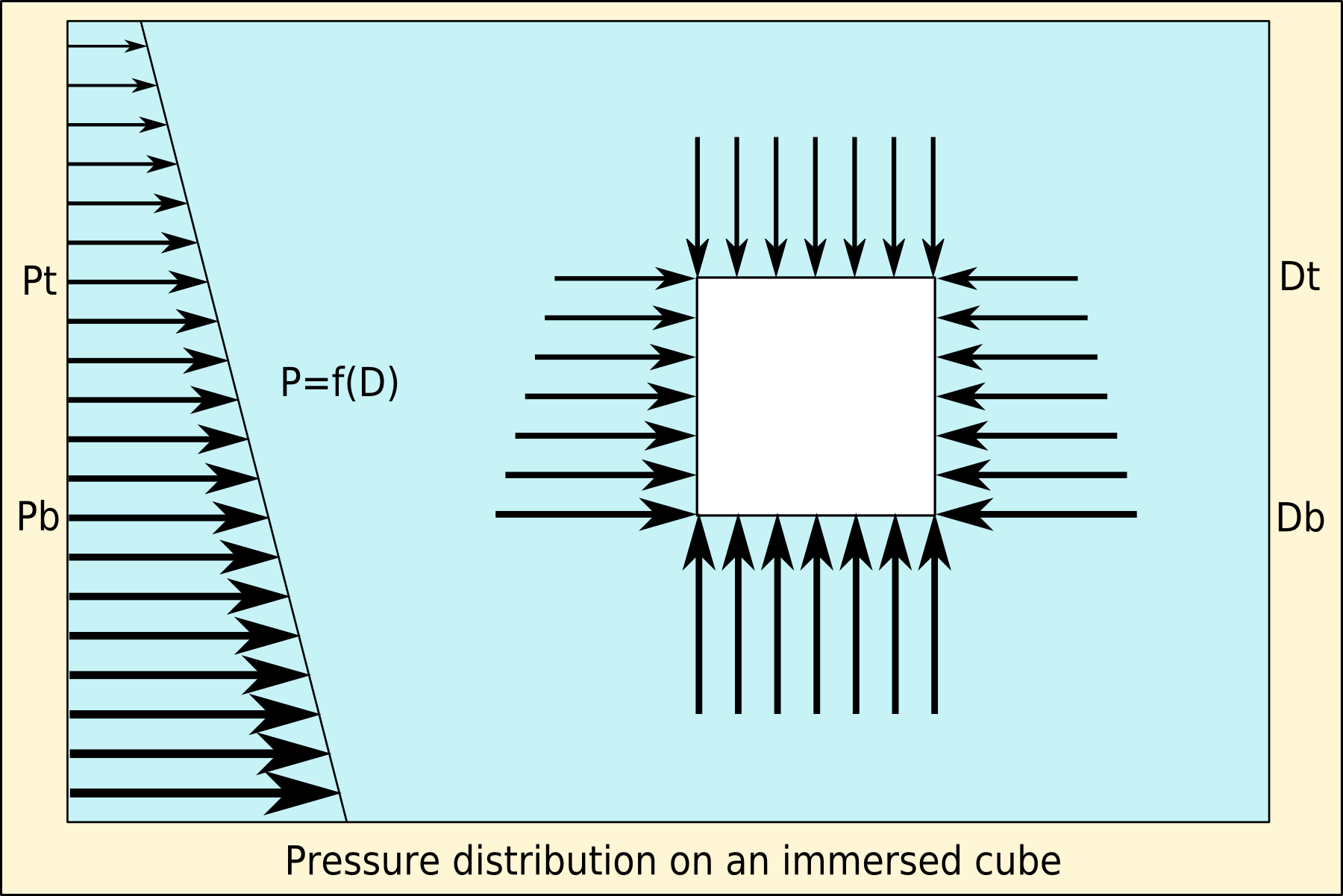
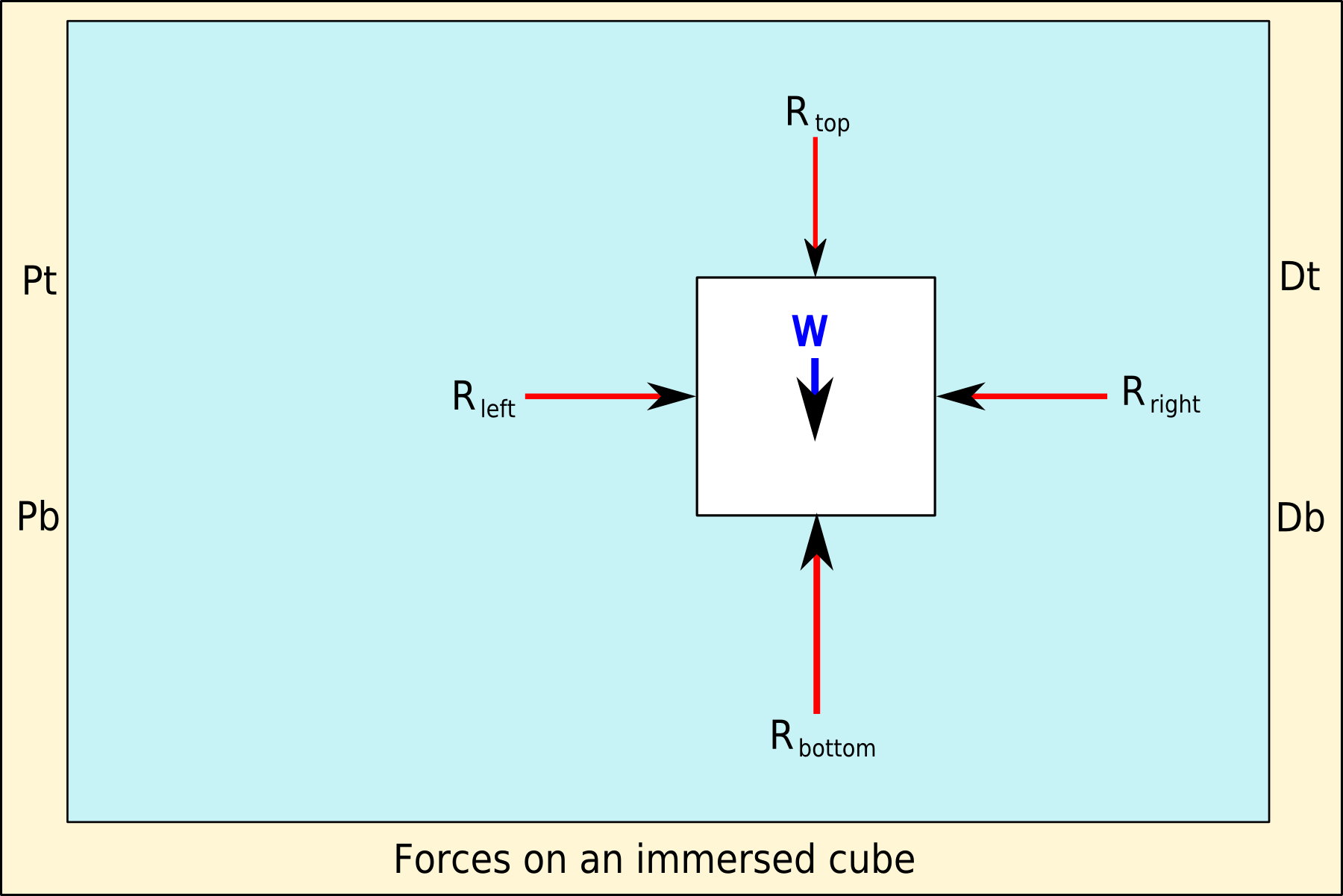
Archimedes' Principle
Archimedes' principle (also spelled Archimedes's principle) states that the upward buoyant force that is exerted on a body immersed in a fluid, whether fully or partially, is equal to the weight of the fluid that the body displaces. Archimedes' principle is a law of physics fundamental to fluid mechanics. It was formulated by Archimedes of Syracuse. Explanation In ''On Floating Bodies'', Archimedes suggested that (c. 246 BC): Archimedes' principle allows the buoyancy of any floating object partially or fully immersed in a fluid to be calculated. The downward force on the object is simply its weight. The upward, or buoyant, force on the object is that stated by Archimedes' principle above. Thus, the net force on the object is the difference between the magnitudes of the buoyant force and its weight. If this net force is positive, the object rises; if negative, the object sinks; and if zero, the object is neutrally buoyant—that is, it remains in place without either rising or ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Buoyancy
Buoyancy (), or upthrust, is an upward force exerted by a fluid that opposes the weight of a partially or fully immersed object. In a column of fluid, pressure increases with depth as a result of the weight of the overlying fluid. Thus the pressure at the bottom of a column of fluid is greater than at the top of the column. Similarly, the pressure at the bottom of an object submerged in a fluid is greater than at the top of the object. The pressure difference results in a net upward force on the object. The magnitude of the force is proportional to the pressure difference, and (as explained by Archimedes' principle) is equivalent to the weight of the fluid that would otherwise occupy the submerged volume of the object, i.e. the displaced fluid. For this reason, an object whose average density is greater than that of the fluid in which it is submerged tends to sink. If the object is less dense than the liquid, the force can keep the object afloat. This can occur only in a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Archimedes
Archimedes of Syracuse (;; ) was a Greek mathematician, physicist, engineer, astronomer, and inventor from the ancient city of Syracuse in Sicily. Although few details of his life are known, he is regarded as one of the leading scientists in classical antiquity. Considered the greatest mathematician of ancient history, and one of the greatest of all time,* * * * * * * * * * Archimedes anticipated modern calculus and analysis by applying the concept of the infinitely small and the method of exhaustion to derive and rigorously prove a range of geometrical theorems. These include the area of a circle, the surface area and volume of a sphere, the area of an ellipse, the area under a parabola, the volume of a segment of a paraboloid of revolution, the volume of a segment of a hyperboloid of revolution, and the area of a spiral. Heath, Thomas L. 1897. ''Works of Archimedes''. Archimedes' other mathematical achievements include deriving an approximation of pi, defining ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ancient Greece
Ancient Greece ( el, Ἑλλάς, Hellás) was a northeastern Mediterranean civilization, existing from the Greek Dark Ages of the 12th–9th centuries BC to the end of classical antiquity ( AD 600), that comprised a loose collection of culturally and linguistically related city-states and other territories. Most of these regions were officially unified only once, for 13 years, under Alexander the Great's empire from 336 to 323 BC (though this excludes a number of Greek city-states free from Alexander's jurisdiction in the western Mediterranean, around the Black Sea, Cyprus, and Cyrenaica). In Western history, the era of classical antiquity was immediately followed by the Early Middle Ages and the Byzantine period. Roughly three centuries after the Late Bronze Age collapse of Mycenaean Greece, Greek urban poleis began to form in the 8th century BC, ushering in the Archaic period and the colonization of the Mediterranean Basin. This was followed by the age of Cl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |


.jpg)
_by_Thomas_Degeorge.png)
.jpg)