|
D'Alembert's Principle
D'Alembert's principle, also known as the Lagrange–d'Alembert principle, is a statement of the fundamental classical physics, classical laws of motion. It is named after its discoverer, the French physicist and mathematician Jean le Rond d'Alembert, and Italian-French mathematician Joseph Louis Lagrange. D'Alembert's principle generalizes the principle of virtual work from statics, static to dynamical systems by introducing ''forces of inertia'' which, when added to the applied forces in a system, result in ''dynamic equilibrium''. D'Alembert's principle can be applied in cases of nonholonomic constraint , kinematic constraints that depend on velocities. The principle does not apply for irreversible displacements, such as sliding friction, and more general specification of the irreversibility is required. Statement of the principle The principle states that the sum of the differences between the forces acting on a system of massive particles and the time derivatives of the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
D'Alembert's Equation
In mathematics, d'Alembert's equation, sometimes also known as Lagrange's equation, is a first order nonlinear ordinary differential equation, named after the French mathematician Jean le Rond d'Alembert Jean-Baptiste le Rond d'Alembert ( ; ; 16 November 1717 – 29 October 1783) was a French mathematician, mechanician, physicist, philosopher, and music theorist. Until 1759 he was, together with Denis Diderot, a co-editor of the ''Encyclopé .... The equation reads asDavis, Harold Thayer. Introduction to nonlinear differential and integral equations. Courier Corporation, 1962. :y = x f\left( \frac \right) + g\left( \frac\right). After differentiating once, and rearranging with p=dy/dx, we have :\frac + \frac=0 The above equation is linear. When f(p)=p, d'Alembert's equation is reduced to Clairaut's equation. References Eponymous equations of physics Mathematical physics Ordinary differential equations {{Mathanalysis-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lectures On Theoretical Physics
''Lectures on Theoretical Physics'' is a six-volume series of physics textbooks translated from Arnold Sommerfeld's classic German texts ''Vorlesungen über Theoretische Physik''. The series includes the volumes ''Mechanics'', ''Mechanics of Deformable Bodies'', ''Electrodynamics'', ''Optics'', ''Thermodynamics and Statistical Mechanics'', and ''Partial Differential Equations in Physics''. Focusing on one subject each semester, the lectures formed a three-year cycle of courses that Sommerfeld repeatedly taught at the University of Munich for over thirty years. Sommerfeld's lectures were famous and he was held to be one of the greatest physics lecturers of his time. Background Sommerfeld was a well known German theoretical physicist who played a major role in developing old quantum theory. He was renowned as a great teacher of theoretical physics in the early 20th century. Wolfgang Pauli wrote in 1951 that Sommerfeld was "the epitome of the scholar and the teacher". Another ph ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Classical Mechanics
Classical mechanics is a Theoretical physics, physical theory describing the motion of objects such as projectiles, parts of Machine (mechanical), machinery, spacecraft, planets, stars, and galaxies. The development of classical mechanics involved Scientific Revolution, substantial change in the methods and philosophy of physics. The qualifier ''classical'' distinguishes this type of mechanics from physics developed after the History of physics#20th century: birth of modern physics, revolutions in physics of the early 20th century, all of which revealed limitations in classical mechanics. The earliest formulation of classical mechanics is often referred to as Newtonian mechanics. It consists of the physical concepts based on the 17th century foundational works of Sir Isaac Newton, and the mathematical methods invented by Newton, Gottfried Wilhelm Leibniz, Leonhard Euler and others to describe the motion of Physical body, bodies under the influence of forces. Later, methods bas ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Thermodynamic System
A thermodynamic system is a body of matter and/or radiation separate from its surroundings that can be studied using the laws of thermodynamics. Thermodynamic systems can be passive and active according to internal processes. According to internal processes, passive systems and active systems are distinguished: passive, in which there is a redistribution of available energy, active, in which one type of energy is converted into another. Depending on its interaction with the environment, a thermodynamic system may be an isolated system, a Closed system#In thermodynamics, closed system, or an Open system (systems theory), open system. An isolated system does not exchange matter or energy with its surroundings. A closed system may exchange heat, experience forces, and exert forces, but does not exchange matter. An open system can interact with its surroundings by exchanging both matter and energy. The physical condition of a thermodynamic system at a given time is described by its ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hamilton's Principle
In physics, Hamilton's principle is William Rowan Hamilton's formulation of the principle of stationary action. It states that the dynamics of a physical system are determined by a variational problem for a functional based on a single function, the Lagrangian, which may contain all physical information concerning the system and the forces acting on it. The variational problem is equivalent to and allows for the derivation of the '' differential'' equations of motion of the physical system. Although formulated originally for classical mechanics, Hamilton's principle also applies to classical fields such as the electromagnetic and gravitational fields, and plays an important role in quantum mechanics, quantum field theory and criticality theories. Mathematical formulation Hamilton's principle states that the true evolution of a system described by generalized coordinates between two specified states and at two specified times and is a stationary point (a point where ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Generalized Forces
In analytical mechanics (particularly Lagrangian mechanics), generalized forces are conjugate to generalized coordinates. They are obtained from the applied forces , acting on a system that has its configuration defined in terms of generalized coordinates. In the formulation of virtual work, each generalized force is the coefficient of the variation of a generalized coordinate. Virtual work Generalized forces can be obtained from the computation of the virtual work, , of the applied forces. The virtual work of the forces, , acting on the particles , is given by \delta W = \sum_^n \mathbf F_i \cdot \delta \mathbf r_i where is the virtual displacement of the particle . Generalized coordinates Let the position vectors of each of the particles, , be a function of the generalized coordinates, . Then the virtual displacements are given by \delta \mathbf_i = \sum_^m \frac \delta q_j,\quad i=1,\ldots, n, where is the virtual displacement of the generalized coordinate . Th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
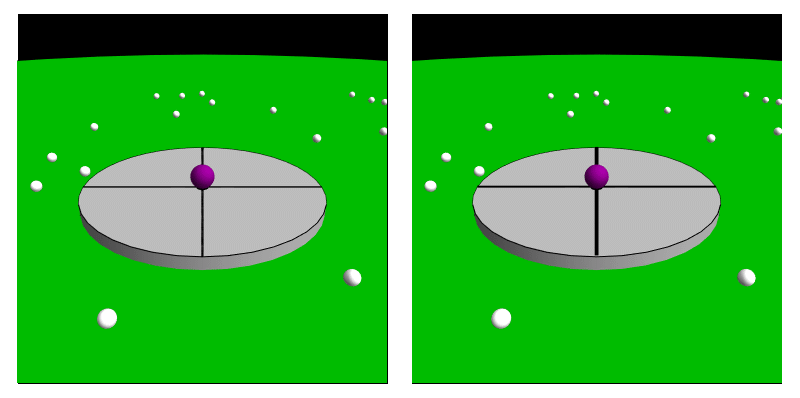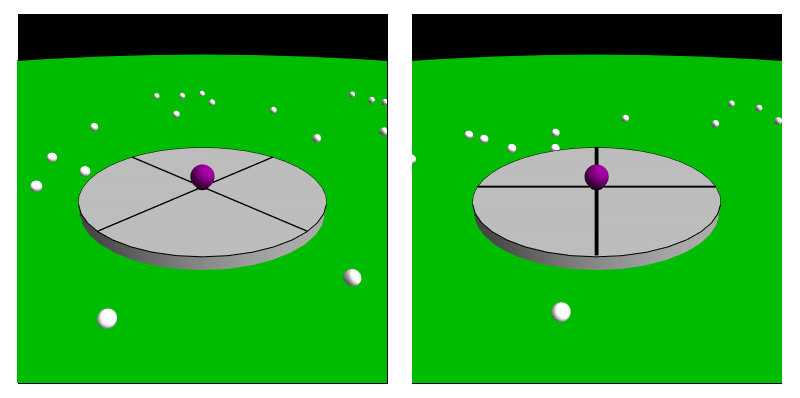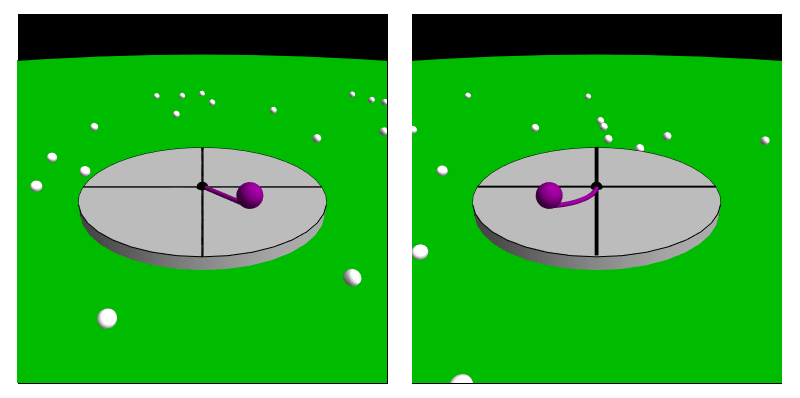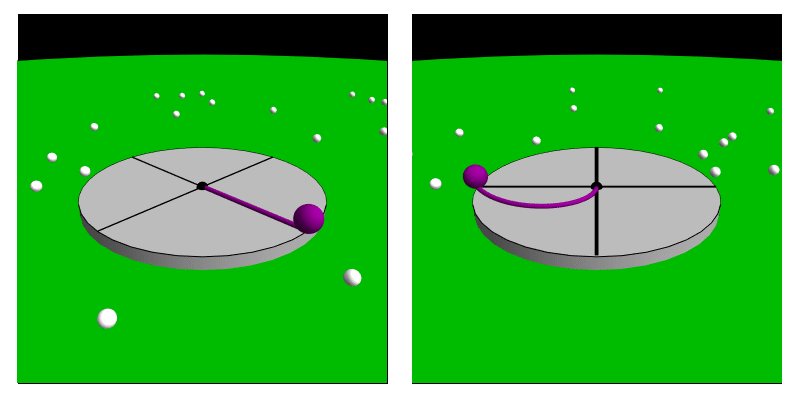
Fictitious Force
A fictitious force, also known as an inertial force or pseudo-force, is a force that appears to act on an object when its motion is described or experienced from a non-inertial reference frame, non-inertial frame of reference. Unlike real forces, which result from physical interactions between objects, fictitious forces occur due to the acceleration of the observer’s frame of reference rather than any actual force acting on a body. These forces are necessary for describing motion correctly within an accelerating frame, ensuring that Newton's laws of motion#Second, Newton's second law of motion remains applicable. Common examples of fictitious forces include the centrifugal force, which appears to push objects outward in a rotating system; the Coriolis force, which affects moving objects in a rotating frame such as the Earth; and the Euler force, which arises when a rotating system changes its angular velocity. While these forces are not real in the sense of being caused by ph ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
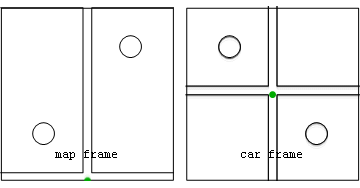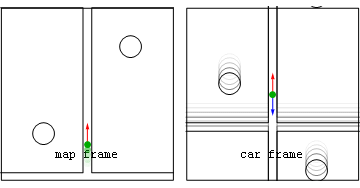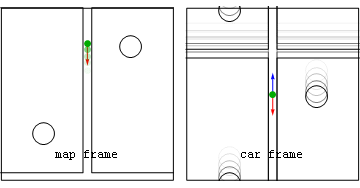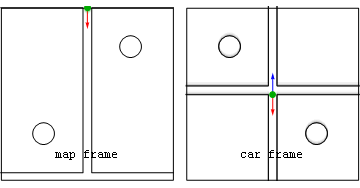
Inertial Reference Frame
In classical physics and special relativity, an inertial frame of reference (also called an inertial space or a Galilean reference frame) is a frame of reference in which objects exhibit inertia: they remain at rest or in uniform motion relative to the frame until acted upon by external forces. In such a frame, the laws of nature can be observed without the need to correct for acceleration. All frames of reference with zero acceleration are in a state of constant rectilinear motion (straight-line motion) with respect to one another. In such a frame, an object with zero net force acting on it, is perceived to move with a constant velocity, or, equivalently, Newton's first law of motion holds. Such frames are known as inertial. Some physicists, like Isaac Newton, originally thought that one of these frames was absolute — the one approximated by the fixed stars. However, this is not required for the definition, and it is now known that those stars are in fact moving, relative t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Non-inertial Reference Frame
A non-inertial reference frame (also known as an accelerated reference frame) is a frame of reference that undergoes acceleration with respect to an inertial frame. An accelerometer at rest in a non-inertial frame will, in general, detect a non-zero acceleration. While the laws of motion are the same in all inertial frames, in non-inertial frames, they vary from frame to frame, depending on the acceleration. In classical mechanics it is often possible to explain the motion of bodies in non-inertial reference frames by introducing additional fictitious forces (also called inertial forces, pseudo-forces, and d'Alembert forces) to Newton's second law. Common examples of this include the Coriolis force and the centrifugal force. In general, the expression for any fictitious force can be derived from the acceleration of the non-inertial frame. As stated by Goodman and Warner, "One might say that F ''m''a holds in any coordinate system provided the term 'force' is redefined to inclu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inertial Force
A fictitious force, also known as an inertial force or pseudo-force, is a force that appears to act on an object when its motion is described or experienced from a non-inertial frame of reference. Unlike real forces, which result from physical interactions between objects, fictitious forces occur due to the acceleration of the observer’s frame of reference rather than any actual force acting on a body. These forces are necessary for describing motion correctly within an accelerating frame, ensuring that Newton's second law of motion remains applicable. Common examples of fictitious forces include the centrifugal force, which appears to push objects outward in a rotating system; the Coriolis force, which affects moving objects in a rotating frame such as the Earth; and the Euler force, which arises when a rotating system changes its angular velocity. While these forces are not real in the sense of being caused by physical interactions, they are essential for accurately analyzi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rudra Pratap
Rudra Pratap is an Indian academician and the vice-chancellor of Plaksha University, Mohali. Previously, he was a professor of Mechanical Engineering at the Indian Institute of Science (IISc), Bangalore. Among other research interests, he works in the field of Microelectromechanical systems (MEMS) and used to head India's first research lab in the field of Microelectromechanical systems, the CranesSci MEMS Lab at Indian Institute of Science, Bangalore. His book on MATLAB ''Getting Started with MATLAB 7'' is popular among the students of engineering. He is also the Chair for the Centre of Nanoscience and Engineering (CeNSE). Pratap is an Associate Editor of Shock and Vibration Journal which publishes articles on various aspects of shocks and vibration including vibration measurements, vibration condition monitoring, shock hardening, fluid-structure interaction, impact biodynamics, vehicle dynamics, and gun dynamics. Education and work Pratap obtained his B.Tech from the In ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inertial Force
A fictitious force, also known as an inertial force or pseudo-force, is a force that appears to act on an object when its motion is described or experienced from a non-inertial frame of reference. Unlike real forces, which result from physical interactions between objects, fictitious forces occur due to the acceleration of the observer’s frame of reference rather than any actual force acting on a body. These forces are necessary for describing motion correctly within an accelerating frame, ensuring that Newton's second law of motion remains applicable. Common examples of fictitious forces include the centrifugal force, which appears to push objects outward in a rotating system; the Coriolis force, which affects moving objects in a rotating frame such as the Earth; and the Euler force, which arises when a rotating system changes its angular velocity. While these forces are not real in the sense of being caused by physical interactions, they are essential for accurately analyzi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |