|
Angle Of Refraction
Snell's law (also known as the Snell–Descartes law, the ibn-Sahl law, and the law of refraction) is a formula used to describe the relationship between the angles of incidence and refraction, when referring to light or other waves passing through a boundary between two different isotropic media, such as water, glass, or air. In optics, the law is used in ray tracing to compute the angles of incidence or refraction, and in experimental optics to find the refractive index of a material. The law is also satisfied in meta-materials, which allow light to be bent "backward" at a negative angle of refraction with a negative refractive index. The law states that, for a given pair of media, the ratio of the sines of angle of incidence \left(\theta_1 \right) and angle of refraction \left(\theta_2\right) is equal to the refractive index of the second medium with regard to the first (n_) which is equal to the ratio of the refractive indices \left(\tfrac\right) of the two media, or e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Snells Law2
Snells is an unincorporated community in the town of Neenah, Winnebago County, Wisconsin Wisconsin ( ) is a U.S. state, state in the Great Lakes region, Great Lakes region of the Upper Midwest of the United States. It borders Minnesota to the west, Iowa to the southwest, Illinois to the south, Lake Michigan to the east, Michig ..., United States. History Snells was named for a local landowner. Notes Unincorporated communities in Winnebago County, Wisconsin Unincorporated communities in Wisconsin {{WinnebagoCountyWI-geo-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Fermat's Principle
Fermat's principle, also known as the principle of least time, is the link between geometrical optics, ray optics and physical optics, wave optics. Fermat's principle states that the path taken by a Ray (optics), ray between two given points is the path that can be traveled in the least time. First proposed by the French mathematician Pierre de Fermat in 1662, as a means of explaining the Snell's law, ordinary law of refraction of light (Fig.1), Fermat's principle was initially controversial because it seemed to ascribe knowledge and intent to nature. Not until the 19th century was it understood that nature's ability to test alternative paths is merely a fundamental property of waves. If points ''A'' and ''B'' are given, a wavefront expanding from ''A'' sweeps all possible ray paths radiating from ''A'', whether they pass through ''B'' or not. If the wavefront reaches point ''B'', it sweeps not only the ''ray'' path(s) from ''A'' to ''B'', but also an infinitude of near ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Cambridge University Press
Cambridge University Press was the university press of the University of Cambridge. Granted a letters patent by King Henry VIII in 1534, it was the oldest university press in the world. Cambridge University Press merged with Cambridge Assessment to form Cambridge University Press and Assessment under Queen Elizabeth II's approval in August 2021. With a global sales presence, publishing hubs, and offices in more than 40 countries, it published over 50,000 titles by authors from over 100 countries. Its publications include more than 420 academic journals, monographs, reference works, school and university textbooks, and English language teaching and learning publications. It also published Bibles, runs a bookshop in Cambridge, sells through Amazon, and has a conference venues business in Cambridge at the Pitt Building and the Sir Geoffrey Cass Sports and Social Centre. It also served as the King's Printer. Cambridge University Press, as part of the University of Cambridge, was a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Book Of Optics
The ''Book of Optics'' (; or ''Perspectiva''; ) is a seven-volume treatise on optics and other fields of study composed by the medieval Arab scholar Ibn al-Haytham, known in the West as Alhazen or Alhacen (965–c. 1040 AD). The ''Book of Optics'' presented experimentally founded arguments against the widely held extramission theory of vision (as held by Euclid in his ''Optica''), and proposed the modern intromission theory, the now accepted model that vision takes place by light entering the eye.D. C. Lindberg (1976), ''Theories of Vision from al-Kindi to Kepler'', Chicago, Univ. of Chicago Press The book is also noted for its early use of the scientific method, its description of the camera obscura, and its formulation of Alhazen's problem. The book extensively affected the development of optics, physics and mathematics in Europe between the 13th and 17th centuries. Vision theory Before the ''Book of Optics'' was written, two theories of vision existed. The extra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Alhazen
Ḥasan Ibn al-Haytham ( Latinized as Alhazen; ; full name ; ) was a medieval mathematician, astronomer, and physicist of the Islamic Golden Age from present-day Iraq.For the description of his main fields, see e.g. ("He is one of the principal Arab mathematicians and, without any doubt, the best physicist.") , ("Ibn al-Ḥaytam was an eminent eleventh-century Arab optician, geometer, arithmetician, algebraist, astronomer, and engineer."), ("Ibn al-Haytham (d. 1039), known in the West as Alhazan, was a leading Arab mathematician, astronomer, and physicist. His optical compendium, Kitab al-Manazir, is the greatest medieval work on optics.") Referred to as "the father of modern optics", he made significant contributions to the principles of optics and visual perception in particular. His most influential work is titled '' Kitāb al-Manāẓir'' (Arabic: , "Book of Optics"), written during 1011–1021, which survived in a Latin edition. The works of Alhazen were frequentl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Isis (journal)
''Isis'' is a quarterly peer-reviewed academic journal published by the University of Chicago Press for the History of Science Society. It covers the history of science, history of medicine, and the history of technology, as well as their cultural influences. It contains original research articles and extensive book reviews and review essays. Furthermore, sections devoted to one particular topic are published in each issue in open access. These sections consist of the Focus section, the Viewpoint section and the Second Look section. History The journal was established by George Sarton and the first issue appeared in March 1913. Contributions were originally in any of four European languages (English, French, German, and Italian), but since the 1920s, only English has been used. Publication is partly supported by an endowment from the Dibner Fund. Two associated publications are ''Osiris'' (established 1936 by Sarton) and the ''Isis Current Bibliography''. The publication o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
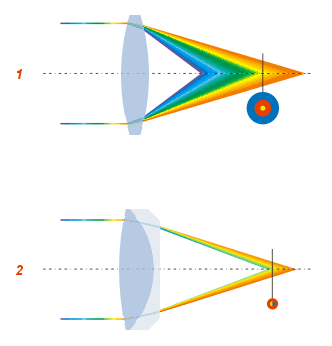
Optical Aberration
In optics, aberration is a property of optical systems, such as Lens (optics), lenses and mirrors, that causes the ''image'' created by the optical system to not be a faithful reproduction of the ''object'' being observed. Aberrations cause the image formed by a lens to be blurred, distorted in shape or have color fringing or other effects not seen in the object, with the nature of the distortion depending on the type of aberration. Aberration can be defined as a departure of the performance of an optical system from the predictions of paraxial optics. In an imaging system, it occurs when light from one point of an object does not converge into (or does not diverge from) a single point after transmission through the system. Aberrations occur because the simple paraxial theory is not a completely accurate model of the effect of an optical system on light, rather than due to flaws in the optical elements. An image-forming optical system with aberration will produce an image which i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Baghdad
Baghdad ( or ; , ) is the capital and List of largest cities of Iraq, largest city of Iraq, located along the Tigris in the central part of the country. With a population exceeding 7 million, it ranks among the List of largest cities in the Arab world, most populous cities in the Middle East and Arab world and forms 22% of the Demographics of Iraq, country's population. Spanning an area of approximately , Baghdad is the capital of its Baghdad Governorate, governorate and serves as Iraq's political, economic, and cultural hub. Founded in 762 AD by Al-Mansur, Baghdad was the capital of the Abbasid Caliphate and became its most notable development project. The city evolved into a cultural and intellectual center of the Muslim world. This, in addition to housing several key academic institutions, including the House of Wisdom, as well as a multi-ethnic and multi-religious environment, garnered it a worldwide reputation as the "Center of Learning". For much of the Abbasid era, duri ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Ibn Sahl (mathematician)
Ibn Sahl (full name: ''Abū Saʿd al-ʿAlāʾ ibn Sahl'' ; c. 940–1000) was a Persian people, Persian mathematician and Islamic physics, physicist of the Islamic Golden Age, associated with the Buyid dynasty, Buyid court of Baghdad. Nothing in his name allows us to glimpse his country of origin. He is known to have written an optical treatise around 984. The text of this treatise was reconstructed by Roshdi Rashed from two manuscripts (edited 1993).: Damascus, al-Ẓāhirīya MS 4871, 3 fols., and Tehran, Millī MS 867, 51 fols. The Tehran manuscript is much longer, but it is badly damaged, and the Damascus manuscript contains a section missing entirely from the Tehran manuscript. The Damascus manuscript has the title ''Fī al-'āla al-muḥriqa'' "On the burning instruments", the Tehran manuscript has a title added in a later hand ''Kitāb al-harrāqāt'' "The book of burners". Ibn Sahl is the first Muslim scholar known to have studied Ptolemy's ''Optics'', and as such an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Willebrord Snellius
Willebrord Snellius (born Willebrord Snel van Royen) (13 June 158030 October 1626) was a Dutch astronomer and mathematician, commonly known as Snell. His name is usually associated with the law of refraction of light known as Snell's law. The lunar crater Snellius is named after Willebrord Snellius. The Royal Netherlands Navy has named three survey ships after Snellius, including a currently-serving vessel. Biography Willebrord Snellius was born in Leiden, Netherlands. In 1613 he succeeded his father, Rudolph Snel van Royen (1546–1613) as professor of mathematics at the University of Leiden. Surveying In 1615, Snellius, after the work of Eratosthenes in Ptolemaic Egypt in the 3rd century BC, probably was the first to use triangulation to do a large-scale arc measurement for determining the circumference of the earth. He was helped in his measurements by two of his students, the Austrian barons Erasmus and Casparus Sterrenberg. In several cities he also received ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Snell Law Of Sines 1837
Snell may refer to: People and fictional characters * Snell (surname), list of people and fictional characters with the surname * Snell (given name), list of people with the name Geography United States * Snell, Virginia, an unincorporated community * Snell, Wisconsin, an unincorporated community * Snell Creek, California * Snell Valley, California Antarctica * Mount Snell Other uses * Snell Acoustics, a manufacturer of audio equipment *Snell Limited, a manufacturer of digital media products * Snell Memorial Foundation, an organization which provides standard of safety for helmets * Snell knot, a hitch knot used to attach an eyed fishing hook to fishing line * Snell station, a light rail station in San Jose, California See also * Snelle (born 1995), Dutch rapper and singer *Snell's law, the law of refraction in optics, named after Willebrord Snellius Willebrord Snellius (born Willebrord Snel van Royen) (13 June 158030 October 1626) was a Dutch astronomer and mathematician, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Confirmation Bias
Confirmation bias (also confirmatory bias, myside bias, or congeniality bias) is the tendency to search for, interpret, favor and recall information in a way that confirms or supports one's prior beliefs or Value (ethics and social sciences), values. People display this bias when they select information that supports their views, ignoring contrary information or when they interpret ambiguous evidence as supporting their existing attitudes. The effect is strongest for desired outcomes, for emotionally charged issues and for deeply entrenched beliefs. Biased search for information, biased interpretation of this information and biased memory recall, have been invoked to explain four specific effects: # ''attitude polarization'' (when a disagreement becomes more extreme even though the different parties are exposed to the same evidence) # ''belief perseverance'' (when beliefs persist after the evidence for them is shown to be false) # the ''irrational primacy effect'' (a greater relia ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |