volatility (finance) on:
[Wikipedia]
[Google]
[Amazon]
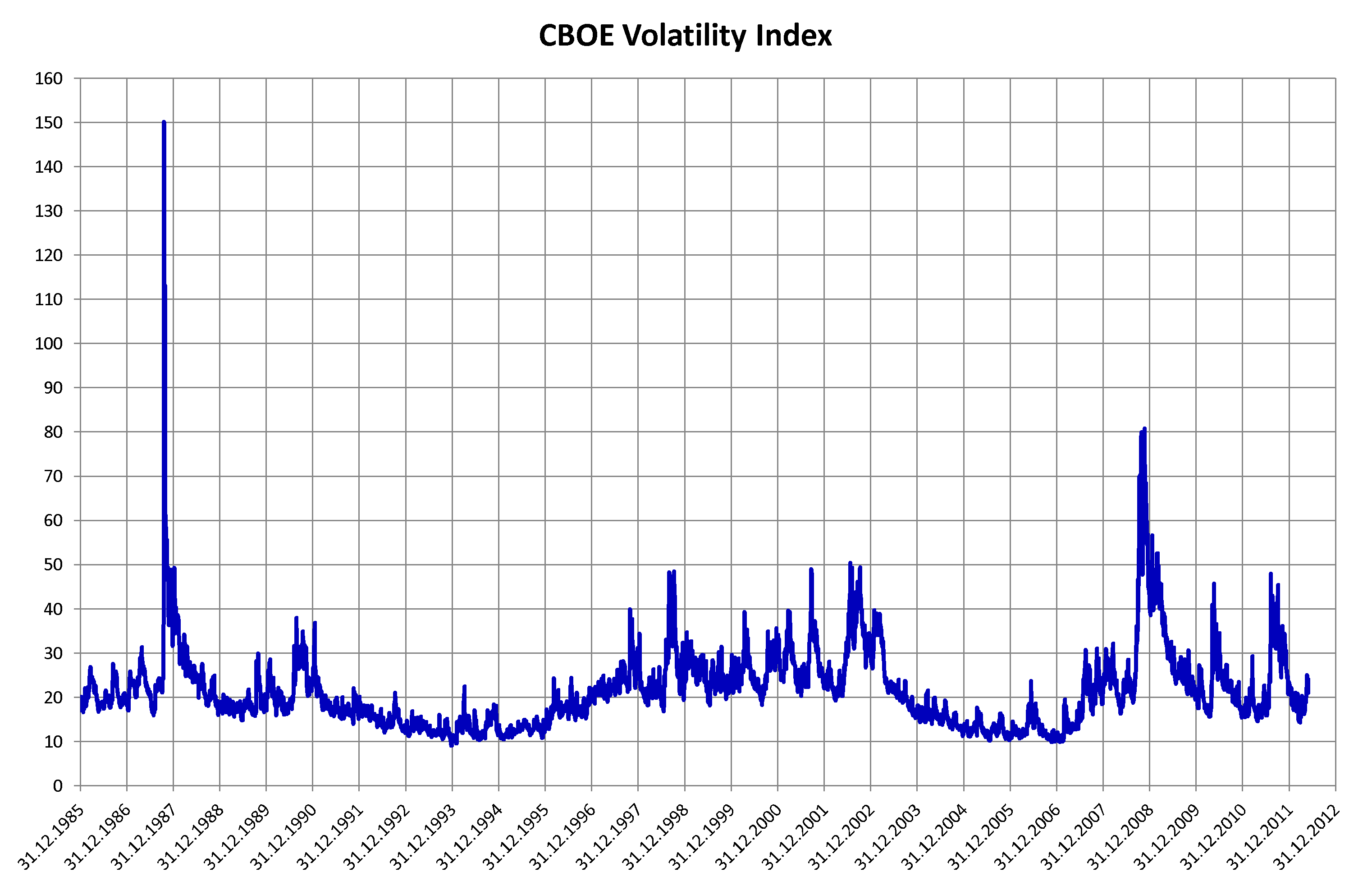 In
In
 Despite the sophisticated composition of most volatility forecasting models, critics claim that their predictive power is similar to that of plain-vanilla measures, such as simple past volatility especially out-of-sample, where different data are used to estimate the models and to test them. Other works have agreed, but claim critics failed to correctly implement the more complicated models. Some practitioners and
Despite the sophisticated composition of most volatility forecasting models, critics claim that their predictive power is similar to that of plain-vanilla measures, such as simple past volatility especially out-of-sample, where different data are used to estimate the models and to test them. Other works have agreed, but claim critics failed to correctly implement the more complicated models. Some practitioners and
Graphical Comparison of Implied and Historical Volatility
video
* ttp://staff.science.uva.nl/~marvisse/volatility.html A short introduction to alternative mathematical concepts of volatility
Volatility estimation from predicted return density
Example based on Google daily return distribution using standard density function
Research paper including excerpt from report entitled Identifying Rich and Cheap Volatility
Excerpt from Enhanced Call Overwriting, a report by Ryan Renicker and Devapriya Mallick at Lehman Brothers (2005).
 In
In finance
Finance is the study and discipline of money, currency and capital assets. It is related to, but not synonymous with economics, the study of production, distribution, and consumption of money, assets, goods and services (the discipline of f ...
, volatility (usually denoted by ''σ'') is the degree of variation of a trading price series over time, usually measured by the standard deviation of logarithmic returns.
Historic volatility measures a time series of past market prices. Implied volatility looks forward in time, being derived from the market price of a market-traded derivative (in particular, an option).
Volatility terminology
Volatility as described here refers to the actual volatility, more specifically: * actual current volatility of a financial instrument for a specified period (for example 30 days or 90 days), based on historical prices over the specified period with the last observation the most recent price. * actual historical volatility which refers to the volatility of a financial instrument over a specified period but with the last observation on a date in the past **near synonymous is realized volatility, thesquare root
In mathematics, a square root of a number is a number such that ; in other words, a number whose '' square'' (the result of multiplying the number by itself, or ⋅ ) is . For example, 4 and −4 are square roots of 16, because .
...
of the realized variance, in turn calculated using the sum of squared returns divided by the number of observations.
* actual future volatility which refers to the volatility of a financial instrument over a specified period starting at the current time and ending at a future date (normally the expiry date of an option)
Now turning to implied volatility, we have:
* historical implied volatility which refers to the implied volatility observed from historical prices of the financial instrument (normally options)
* current implied volatility which refers to the implied volatility observed from current prices of the financial instrument
* future implied volatility which refers to the implied volatility observed from future prices of the financial instrument
For a financial instrument whose price follows a Gaussian
Carl Friedrich Gauss (1777–1855) is the eponym of all of the topics listed below.
There are over 100 topics all named after this German mathematician and scientist, all in the fields of mathematics, physics, and astronomy. The English eponym ...
random walk
In mathematics, a random walk is a random process that describes a path that consists of a succession of random steps on some mathematical space.
An elementary example of a random walk is the random walk on the integer number line \mathbb Z ...
, or Wiener process
In mathematics, the Wiener process is a real-valued continuous-time stochastic process named in honor of American mathematician Norbert Wiener for his investigations on the mathematical properties of the one-dimensional Brownian motion. It is ...
, the width of the distribution increases as time increases. This is because there is an increasing probability
Probability is the branch of mathematics concerning numerical descriptions of how likely an event is to occur, or how likely it is that a proposition is true. The probability of an event is a number between 0 and 1, where, roughly speaking, ...
that the instrument's price will be farther away from the initial price as time increases. However, rather than increase linearly, the volatility increases with the square-root of time as time increases, because some fluctuations are expected to cancel each other out, so the most likely deviation after twice the time will not be twice the distance from zero.
Since observed price changes do not follow Gaussian distributions, others such as the Lévy distribution are often used. These can capture attributes such as " fat tails".
Volatility is a statistical measure of dispersion around the average of any random variable such as market parameters etc.
Mathematical definition
For any fund that evolves randomly with time, volatility is defined as the standard deviation of a sequence of random variables, each of which is the return of the fund over some corresponding sequence of (equally sized) times. Thus, "annualized" volatility is the standard deviation of an instrument's yearly logarithmic returns. The generalized volatility fortime horizon
Time is the continued sequence of existence and events that occurs in an apparently irreversible succession from the past, through the present, into the future. It is a component quantity of various measurements used to sequence events, to co ...
''T'' in years is expressed as:
:
Therefore, if the daily logarithmic returns of a stock have a standard deviation of and the time period of returns is ''P'' in trading days, the annualized volatility is
:
A common assumption is that ''P'' = 252 trading days in any given year. Then, if = 0.01, the annualized volatility is
:
The monthly volatility (i.e., ''T'' = 1/12 of a year or ''P'' = 252/12 = 21 trading days) would be
:
:
The formulas used above to convert returns or volatility measures from one time period to another assume a particular underlying model or process. These formulas are accurate extrapolations of a random walk
In mathematics, a random walk is a random process that describes a path that consists of a succession of random steps on some mathematical space.
An elementary example of a random walk is the random walk on the integer number line \mathbb Z ...
, or Wiener process, whose steps have finite variance. However, more generally, for natural stochastic processes, the precise relationship between volatility measures for different time periods is more complicated. Some use the Lévy stability exponent ''α'' to extrapolate natural processes:
:
If ''α'' = 2 the Wiener process
In mathematics, the Wiener process is a real-valued continuous-time stochastic process named in honor of American mathematician Norbert Wiener for his investigations on the mathematical properties of the one-dimensional Brownian motion. It is ...
scaling relation is obtained, but some people believe ''α'' < 2 for financial activities such as stocks, indexes and so on. This was discovered by Benoît Mandelbrot, who looked at cotton prices and found that they followed a Lévy alpha-stable distribution with ''α'' = 1.7. (See New Scientist, 19 April 1997.)
Volatility origin
Much research has been devoted to modeling and forecasting the volatility of financial returns, and yet few theoretical models explain how volatility comes to exist in the first place. Roll (1984) shows that volatility is affected by market microstructure. Glosten and Milgrom (1985) shows that at least one source of volatility can be explained by the liquidity provision process. When market makers infer the possibility of adverse selection, they adjust their trading ranges, which in turn increases the band of price oscillation. In September 2019,JPMorgan Chase
JPMorgan Chase & Co. is an American multinational investment bank and financial services holding company headquartered in New York City and incorporated in Delaware. As of 2022, JPMorgan Chase is the largest bank in the United States, t ...
determined the effect of US President Donald Trump
Donald John Trump (born June 14, 1946) is an American politician, media personality, and businessman who served as the 45th president of the United States from 2017 to 2021.
Trump graduated from the Wharton School of the University of P ...
's tweets, and called it the Volfefe index combining volatility and the covfefe meme
A meme ( ) is an idea, behavior, or style that spreads by means of imitation from person to person within a culture and often carries symbolic meaning representing a particular phenomenon or theme. A meme acts as a unit for carrying cultural ...
.
Volatility for investors
Investors care about volatility for at least eight reasons: # The wider the swings in an investment's price, the harder emotionally it is to not worry; # Price volatility of a trading instrument can define position sizing in a portfolio; # When certain cash flows from selling a security are needed at a specific future date, higher volatility means a greater chance of a shortfall; # Higher volatility of returns while saving for retirement results in a wider distribution of possible final portfolio values; # Higher volatility of return when retired gives withdrawals a larger permanent impact on the portfolio's value; # Price volatility presents opportunities to buy assets cheaply and sell when overpriced; # Portfolio volatility has a negative impact on the compound annual growth rate (CAGR) of that portfolio # Volatility affects pricing ofoptions
Option or Options may refer to:
Computing
*Option key, a key on Apple computer keyboards
*Option type, a polymorphic data type in programming languages
*Command-line option, an optional parameter to a command
*OPTIONS, an HTTP request method
...
, being a parameter of the Black–Scholes model.
In today's markets, it is also possible to trade volatility directly, through the use of derivative securities such as options and variance swap A variance swap is an over-the-counter financial derivative that allows one to speculate on or hedge risks associated with the magnitude of movement, i.e. volatility, of some underlying product, like an exchange rate, interest rate, or stock inde ...
s. See Volatility arbitrage.
Volatility versus direction
Volatility does not measure the direction of price changes, merely their dispersion. This is because when calculating standard deviation (orvariance
In probability theory and statistics, variance is the expectation of the squared deviation of a random variable from its population mean or sample mean. Variance is a measure of dispersion, meaning it is a measure of how far a set of numbe ...
), all differences are squared, so that negative and positive differences are combined into one quantity. Two instruments with different volatilities may have the same expected return, but the instrument with higher volatility will have larger swings in values over a given period of time.
For example, a lower volatility stock may have an expected (average) return of 7%, with annual volatility of 5%. This would indicate returns from approximately negative 3% to positive 17% most of the time (19 times out of 20, or 95% via a two standard deviation rule). A higher volatility stock, with the same expected return of 7% but with annual volatility of 20%, would indicate returns from approximately negative 33% to positive 47% most of the time (19 times out of 20, or 95%). These estimates assume a normal distribution
In statistics, a normal distribution or Gaussian distribution is a type of continuous probability distribution for a real-valued random variable. The general form of its probability density function is
:
f(x) = \frac e^
The parameter \mu ...
; in reality stocks are found to be leptokurtotic.
Volatility over time
Although the Black-Scholes equation assumes predictable constant volatility, this is not observed in real markets, and amongst the models are Emanuel Derman and Iraj Kani's and Bruno Dupire's local volatility, Poisson process where volatility jumps to new levels with a predictable frequency, and the increasingly popular Heston model of stochastic volatility. ink broken It is common knowledge that types of assets experience periods of high and low volatility. That is, during some periods, prices go up and down quickly, while during other times they barely move at all. Inforeign exchange market
The foreign exchange market (Forex, FX, or currency market) is a global decentralized or over-the-counter (OTC) market for the trading of currencies. This market determines foreign exchange rates for every currency. It includes all as ...
, price changes are seasonally heteroskedastic with periods of one day and one week.
Periods when prices fall quickly (a crash
Crash or CRASH may refer to:
Common meanings
* Collision, an impact between two or more objects
* Crash (computing), a condition where a program ceases to respond
* Cardiac arrest, a medical condition in which the heart stops beating
* Couch ...
) are often followed by prices going down even more, or going up by an unusual amount. Also, a time when prices rise quickly (a possible bubble
Bubble, Bubbles or The Bubble may refer to:
Common uses
* Bubble (physics), a globule of one substance in another, usually gas in a liquid
** Soap bubble
* Economic bubble, a situation where asset prices are much higher than underlying fund ...
) may often be followed by prices going up even more, or going down by an unusual amount.
Most typically, extreme movements do not appear 'out of nowhere'; they are presaged by larger movements than usual. This is termed autoregressive conditional heteroskedasticity. Whether such large movements have the same direction, or the opposite, is more difficult to say. And an increase in volatility does not always presage a further increase—the volatility may simply go back down again.
Not only the volatility depends on the period when it is measured but also on the selected time resolution. The effect is observed due to the fact that the information flow between short-term and long-term traders is asymmetric. As a result, volatility measured with high resolution contains information that is not covered by low resolution volatility and vice versa.
The risk parity weighted volatility of the three assets Gold, Treasury bonds and Nasdaq acting as proxy for the Marketportfolio seems to have a low point at 4% after turning upwards for the 8th time since 1974 at this reading in the summer of 2014.
Alternative measures of volatility
Some authors point out that realized volatility and implied volatility are backward and forward looking measures, and do not reflect current volatility. To address that issue an alternative, ensemble measures of volatility were suggested. One of the measures is defined as the standard deviation of ensemble returns instead of time series of returns. Another considers the regular sequence of directional-changes as the proxy for the instantaneous volatility.Implied volatility parametrisation
There exist several known parametrisations of the implied volatility surface, Schonbucher, SVI and .http://www.readcube.com/articles/10.1002/wilm.10201?locale=enCrude volatility estimation
Using a simplification of the above formula it is possible to estimate annualized volatility based solely on approximate observations. Suppose you notice that a market price index, which has a current value near 10,000, has moved about 100 points a day, on average, for many days. This would constitute a 1% daily movement, up or down. To annualize this, you can use the "rule of 16", that is, multiply by 16 to get 16% as the annual volatility. The rationale for this is that 16 is the square root of 256, which is approximately the number of trading days in a year (252). This also uses the fact that the standard deviation of the sum of ''n'' independent variables (with equal standard deviations) is √n times the standard deviation of the individual variables. The average magnitude of the observations is merely an approximation of the standard deviation of the market index. Assuming that the market index daily changes are normally distributed with mean zero and standard deviation ''σ'', the expected value of the magnitude of the observations is √(2/)''σ'' = 0.798''σ''. The net effect is that this crude approach underestimates the true volatility by about 20%.Estimate of compound annual growth rate (CAGR)
Consider theTaylor series
In mathematics, the Taylor series or Taylor expansion of a function is an infinite sum of terms that are expressed in terms of the function's derivatives at a single point. For most common functions, the function and the sum of its Taylor ser ...
:
:
Taking only the first two terms one has:
:
Volatility thus mathematically represents a drag on the CAGR (formalized as the " volatility tax"). Realistically, most financial assets have negative skewness and leptokurtosis, so this formula tends to be over-optimistic. Some people use the formula:
:
for a rough estimate, where ''k'' is an empirical factor (typically five to ten).
Criticisms of volatility forecasting models
 Despite the sophisticated composition of most volatility forecasting models, critics claim that their predictive power is similar to that of plain-vanilla measures, such as simple past volatility especially out-of-sample, where different data are used to estimate the models and to test them. Other works have agreed, but claim critics failed to correctly implement the more complicated models. Some practitioners and
Despite the sophisticated composition of most volatility forecasting models, critics claim that their predictive power is similar to that of plain-vanilla measures, such as simple past volatility especially out-of-sample, where different data are used to estimate the models and to test them. Other works have agreed, but claim critics failed to correctly implement the more complicated models. Some practitioners and portfolio managers A portfolio manager (PM) is a professional responsible for making investment decisions and carrying out investment activities on behalf of vested individuals or institutions. Clients invest their money into the PM's investment policy for future gro ...
seem to completely ignore or dismiss volatility forecasting models. For example, Nassim Taleb famously titled one of his '' Journal of Portfolio Management'' papers "We Don't Quite Know What We are Talking About When We Talk About Volatility". In a similar note, Emanuel Derman expressed his disillusion with the enormous supply of empirical models unsupported by theory.Derman, Emanuel (2011): Models.Behaving.Badly: Why Confusing Illusion With Reality Can Lead to Disaster, on Wall Street and in Life”, Ed. Free Press. He argues that, while "theories are attempts to uncover the hidden principles underpinning the world around us, as Albert Einstein did with his theory of relativity", we should remember that "models are metaphors – analogies that describe one thing relative to another".
See also
* Beta (finance) *Dispersion
Dispersion may refer to:
Economics and finance
*Dispersion (finance), a measure for the statistical distribution of portfolio returns
*Price dispersion, a variation in prices across sellers of the same item
*Wage dispersion, the amount of variatio ...
* Financial economics
Financial economics, also known as finance, is the branch of economics characterized by a "concentration on monetary activities", in which "money of one type or another is likely to appear on ''both sides'' of a trade". William F. Sharpe"Financia ...
* IVX
* Jules Regnault Jules Augustin Frédéric Regnault (; 1 February 1834, Béthencourt – 9 December 1894, Paris) was a French stock broker's assistant who first suggested a modern theory of stock price changes i''Calcul des Chances et Philosophie de la Bourse' ...
* Risk
In simple terms, risk is the possibility of something bad happening. Risk involves uncertainty about the effects/implications of an activity with respect to something that humans value (such as health, well-being, wealth, property or the environm ...
* VIX
* Volatility smile
* Volatility tax
References
External links
Graphical Comparison of Implied and Historical Volatility
video
* ttp://staff.science.uva.nl/~marvisse/volatility.html A short introduction to alternative mathematical concepts of volatility
Volatility estimation from predicted return density
Example based on Google daily return distribution using standard density function
Research paper including excerpt from report entitled Identifying Rich and Cheap Volatility
Excerpt from Enhanced Call Overwriting, a report by Ryan Renicker and Devapriya Mallick at Lehman Brothers (2005).
Further reading
* * {{Use dmy dates, date=August 2014 Mathematical finance Technical analysis