Trigonometry on:
[Wikipedia]
[Google]
[Amazon]
Trigonometry () is a branch of mathematics that studies relationships between side lengths and angles of
 Sumerian astronomers studied angle measure, using a division of circles into 360 degrees. They, and later the
Sumerian astronomers studied angle measure, using a division of circles into 360 degrees. They, and later the
 Trigonometric ratios are the ratios between edges of a right triangle. These ratios are given by the following
Trigonometric ratios are the ratios between edges of a right triangle. These ratios are given by the following
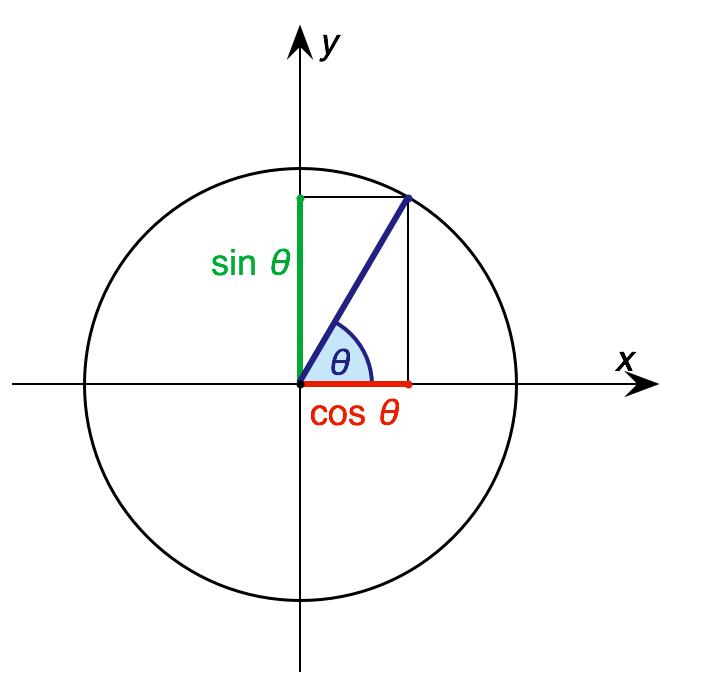
 Trigonometric ratios can also be represented using the unit circle, which is the circle of radius 1 centered at the origin in the plane. In this setting, the terminal side of an angle ''A'' placed in standard position will intersect the unit circle in a point (x,y), where and . This representation allows for the calculation of commonly found trigonometric values, such as those in the following table:
Trigonometric ratios can also be represented using the unit circle, which is the circle of radius 1 centered at the origin in the plane. In this setting, the terminal side of an angle ''A'' placed in standard position will intersect the unit circle in a point (x,y), where and . This representation allows for the calculation of commonly found trigonometric values, such as those in the following table:
 Historically, trigonometry has been used for locating latitudes and longitudes of sailing vessels, plotting courses, and calculating distances during navigation.
Trigonometry is still used in navigation through such means as the
Historically, trigonometry has been used for locating latitudes and longitudes of sailing vessels, plotting courses, and calculating distances during navigation.
Trigonometry is still used in navigation through such means as the
 The sine and cosine functions are fundamental to the theory of periodic functions, such as those that describe sound and
The sine and cosine functions are fundamental to the theory of periodic functions, such as those that describe sound and
 Trigonometry has been noted for its many identities, that is, equations that are true for all possible inputs.
Identities involving only angles are known as ''trigonometric identities''. Other equations, known as ''triangle identities'', relate both the sides and angles of a given triangle.
Trigonometry has been noted for its many identities, that is, equations that are true for all possible inputs.
Identities involving only angles are known as ''trigonometric identities''. Other equations, known as ''triangle identities'', relate both the sides and angles of a given triangle.
Extract of page 856
/ref> : : : The second and third equations are derived from dividing the first equation by and , respectively.
Khan Academy: Trigonometry, free online micro lectures
by Alfred Monroe Kenyon and Louis Ingold, The Macmillan Company, 1914. In images, full text presented.
Benjamin Banneker's Trigonometry Puzzle
a
Convergence
Dave's Short Course in Trigonometry
by David Joyce of Clark University
Trigonometry, by Michael Corral, Covers elementary trigonometry, Distributed under GNU Free Documentation License
{{Authority control
triangle
A triangle is a polygon with three edges and three vertices. It is one of the basic shapes in geometry. A triangle with vertices ''A'', ''B'', and ''C'' is denoted \triangle ABC.
In Euclidean geometry, any three points, when non- colline ...
s. The field emerged in the Hellenistic world during the 3rd century BC from applications of geometry
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is ...
to astronomical studies. The Greeks focused on the calculation of chords, while mathematicians in India created the earliest-known tables of values for trigonometric ratios (also called trigonometric functions) such as sine.
Throughout history, trigonometry has been applied in areas such as geodesy, surveying, celestial mechanics, and navigation
Navigation is a field of study that focuses on the process of monitoring and controlling the movement of a craft or vehicle from one place to another.Bowditch, 2003:799. The field of navigation includes four general categories: land navigation, ...
.
Trigonometry is known for its many identities. These
trigonometric identities
In trigonometry, trigonometric identities are equalities that involve trigonometric functions and are true for every value of the occurring variables for which both sides of the equality are defined. Geometrically, these are identities involvin ...
are commonly used for rewriting trigonometrical expression
Expression may refer to:
Linguistics
* Expression (linguistics), a word, phrase, or sentence
* Fixed expression, a form of words with a specific meaning
* Idiom, a type of fixed expression
* Metaphorical expression, a particular word, phrase, o ...
s with the aim to simplify an expression, to find a more useful form of an expression, or to solve an equation.
History
 Sumerian astronomers studied angle measure, using a division of circles into 360 degrees. They, and later the
Sumerian astronomers studied angle measure, using a division of circles into 360 degrees. They, and later the Babylonians
Babylonia (; Akkadian: , ''māt Akkadī'') was an ancient Akkadian-speaking state and cultural area based in the city of Babylon in central-southern Mesopotamia (present-day Iraq and parts of Syria). It emerged as an Amorite-ruled state c. 1 ...
, studied the ratios of the sides of similar triangles and discovered some properties of these ratios but did not turn that into a systematic method for finding sides and angles of triangles. The ancient Nubians used a similar method.
In the 3rd century BC, Hellenistic mathematicians such as Euclid and Archimedes studied the properties of chords
Chord may refer to:
* Chord (music), an aggregate of musical pitches sounded simultaneously
** Guitar chord a chord played on a guitar, which has a particular tuning
* Chord (geometry), a line segment joining two points on a curve
* Chord ( ...
and inscribed angles in circles, and they proved theorems that are equivalent to modern trigonometric formulae, although they presented them geometrically rather than algebraically. In 140 BC, Hipparchus (from Nicaea, Asia Minor) gave the first tables of chords, analogous to modern tables of sine values, and used them to solve problems in trigonometry and spherical trigonometry
Spherical trigonometry is the branch of spherical geometry that deals with the metrical relationships between the sides and angles of spherical triangles, traditionally expressed using trigonometric functions. On the sphere, geodesics are grea ...
. In the 2nd century AD, the Greco-Egyptian astronomer Ptolemy (from Alexandria, Egypt) constructed detailed trigonometric tables ( Ptolemy's table of chords) in Book 1, chapter 11 of his '' Almagest''. Ptolemy used chord length to define his trigonometric functions, a minor difference from the sine convention we use today. (The value we call sin(θ) can be found by looking up the chord length for twice the angle of interest (2θ) in Ptolemy's table, and then dividing that value by two.) Centuries passed before more detailed tables were produced, and Ptolemy's treatise remained in use for performing trigonometric calculations in astronomy throughout the next 1200 years in the medieval Byzantine
The Byzantine Empire, also referred to as the Eastern Roman Empire or Byzantium, was the continuation of the Roman Empire primarily in its eastern provinces during Late Antiquity and the Middle Ages, when its capital city was Constantinopl ...
, Islamic, and, later, Western European worlds.
The modern sine convention is first attested in the '' Surya Siddhanta'', and its properties were further documented by the 5th century (AD) Indian mathematician and astronomer Aryabhata
Aryabhata ( ISO: ) or Aryabhata I (476–550 CE) was an Indian mathematician and astronomer of the classical age of Indian mathematics and Indian astronomy. He flourished in the Gupta Era and produced works such as the ''Aryabhatiya'' (which ...
. These Greek and Indian works were translated and expanded by medieval Islamic mathematicians. By the 10th century, Islamic mathematicians were using all six trigonometric functions, had tabulated their values, and were applying them to problems in spherical geometry. The Persian
Persian may refer to:
* People and things from Iran, historically called ''Persia'' in the English language
** Persians, the majority ethnic group in Iran, not to be conflated with the Iranic peoples
** Persian language, an Iranian language of the ...
polymath
A polymath ( el, πολυμαθής, , "having learned much"; la, homo universalis, "universal human") is an individual whose knowledge spans a substantial number of subjects, known to draw on complex bodies of knowledge to solve specific pro ...
Nasir al-Din al-Tusi has been described as the creator of trigonometry as a mathematical discipline in its own right. He was the first to treat trigonometry as a mathematical discipline independent from astronomy, and he developed spherical trigonometry into its present form. He listed the six distinct cases of a right-angled triangle in spherical trigonometry, and in his ''On the Sector Figure'', he stated the law of sines for plane and spherical triangles, discovered the law of tangents for spherical triangles, and provided proofs for both these laws. Knowledge of trigonometric functions and methods reached Western Europe
Western Europe is the western region of Europe. The region's countries and territories vary depending on context.
The concept of "the West" appeared in Europe in juxtaposition to "the East" and originally applied to the ancient Mediterranean ...
via Latin translations of Ptolemy's Greek ''Almagest'' as well as the works of Persian and Arab astronomers such as Al Battani and Nasir al-Din al-Tusi. One of the earliest works on trigonometry by a northern European mathematician is ''De Triangulis'' by the 15th century German mathematician Regiomontanus
Johannes Müller von Königsberg (6 June 1436 – 6 July 1476), better known as Regiomontanus (), was a mathematician, astrologer and astronomer of the German Renaissance, active in Vienna, Buda and Nuremberg. His contributions were instrument ...
, who was encouraged to write, and provided with a copy of the ''Almagest'', by the Byzantine Greek scholar cardinal Basilios Bessarion
Bessarion ( el, Βησσαρίων; 2 January 1403 – 18 November 1472) was a Byzantine Greek Renaissance humanist, theologian, Catholic cardinal and one of the famed Greek scholars who contributed to the so-called great revival of letters ...
with whom he lived for several years. At the same time, another translation of the ''Almagest'' from Greek into Latin was completed by the Cretan George of Trebizond
George of Trebizond ( el, Γεώργιος Τραπεζούντιος; 1395–1486) was a Byzantine Greek philosopher, scholar, and humanist. Life
He was born on the Greek island of Crete (then a Venetian colony known as the Kingdom of Candia), a ...
. Trigonometry was still so little known in 16th-century northern Europe that Nicolaus Copernicus
Nicolaus Copernicus (; pl, Mikołaj Kopernik; gml, Niklas Koppernigk, german: Nikolaus Kopernikus; 19 February 1473 – 24 May 1543) was a Renaissance polymath, active as a mathematician, astronomer, and Catholic canon, who formulated ...
devoted two chapters of '' De revolutionibus orbium coelestium'' to explain its basic concepts.
Driven by the demands of navigation
Navigation is a field of study that focuses on the process of monitoring and controlling the movement of a craft or vehicle from one place to another.Bowditch, 2003:799. The field of navigation includes four general categories: land navigation, ...
and the growing need for accurate maps of large geographic areas, trigonometry grew into a major branch of mathematics. Bartholomaeus Pitiscus was the first to use the word, publishing his ''Trigonometria'' in 1595. Gemma Frisius described for the first time the method of triangulation still used today in surveying. It was Leonhard Euler who fully incorporated complex number
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the fo ...
s into trigonometry. The works of the Scottish mathematicians James Gregory in the 17th century and Colin Maclaurin
Colin Maclaurin (; gd, Cailean MacLabhruinn; February 1698 – 14 June 1746) was a Scottish mathematician who made important contributions to geometry and algebra. He is also known for being a child prodigy and holding the record for bei ...
in the 18th century were influential in the development of trigonometric series
In mathematics, a trigonometric series is a infinite series of the form
: \frac+\displaystyle\sum_^(A_ \cos + B_ \sin),
an infinite version of a trigonometric polynomial.
It is called the Fourier series of the integrable function f if the term ...
. Also in the 18th century, Brook Taylor defined the general Taylor series.
Trigonometric ratios
trigonometric function
In mathematics, the trigonometric functions (also called circular functions, angle functions or goniometric functions) are real functions which relate an angle of a right-angled triangle to ratios of two side lengths. They are widely used in a ...
s of the known angle ''A'', where ''a'', '' b'' and ''h'' refer to the lengths of the sides in the accompanying figure:
* Sine function (sin), defined as the ratio of the side opposite the angle to the hypotenuse
In geometry, a hypotenuse is the longest side of a right-angled triangle, the side opposite the right angle. The length of the hypotenuse can be found using the Pythagorean theorem, which states that the square of the length of the hypotenuse e ...
.
::
* Cosine function (cos), defined as the ratio of the adjacent leg (the side of the triangle joining the angle to the right angle) to the hypotenuse.
::
* Tangent
In geometry, the tangent line (or simply tangent) to a plane curve at a given point is the straight line that "just touches" the curve at that point. Leibniz defined it as the line through a pair of infinitely close points on the curve. Mo ...
function (tan), defined as the ratio of the opposite leg to the adjacent leg.
::
The hypotenuse
In geometry, a hypotenuse is the longest side of a right-angled triangle, the side opposite the right angle. The length of the hypotenuse can be found using the Pythagorean theorem, which states that the square of the length of the hypotenuse e ...
is the side opposite to the 90 degree angle in a right triangle; it is the longest side of the triangle and one of the two sides adjacent to angle ''A''. The adjacent leg is the other side that is adjacent to angle ''A''. The opposite side is the side that is opposite to angle ''A''. The terms perpendicular and base are sometimes used for the opposite and adjacent sides respectively. See below under Mnemonics
A mnemonic ( ) device, or memory device, is any learning technique that aids information retention or retrieval (remembering) in the human memory for better understanding.
Mnemonics make use of elaborative encoding, retrieval cues, and imager ...
.
Since any two right triangles with the same acute angle ''A'' are similar, the value of a trigonometric ratio depends only on the angle ''A''.
The reciprocals of these functions are named the cosecant (csc), secant (sec), and cotangent (cot), respectively:
:
:
:
The cosine, cotangent, and cosecant are so named because they are respectively the sine, tangent, and secant of the complementary angle abbreviated to "co-".
With these functions, one can answer virtually all questions about arbitrary triangles by using the law of sines
In trigonometry, the law of sines, sine law, sine formula, or sine rule is an equation relating the lengths of the sides of any triangle to the sines of its angles. According to the law,
\frac \,=\, \frac \,=\, \frac \,=\, 2R,
where , and ar ...
and the law of cosines
In trigonometry, the law of cosines (also known as the cosine formula, cosine rule, or al-Kashi's theorem) relates the lengths of the sides of a triangle to the cosine of one of its angles. Using notation as in Fig. 1, the law of cosines states ...
. These laws can be used to compute the remaining angles and sides of any triangle as soon as two sides and their included angle or two angles and a side or three sides are known.
Mnemonics
A common use ofmnemonic
A mnemonic ( ) device, or memory device, is any learning technique that aids information retention or retrieval (remembering) in the human memory for better understanding.
Mnemonics make use of elaborative encoding, retrieval cues, and imag ...
s is to remember facts and relationships in trigonometry. For example, the ''sine'', ''cosine'', and ''tangent'' ratios in a right triangle can be remembered by representing them and their corresponding sides as strings of letters. For instance, a mnemonic is SOH-CAH-TOA:
:Sine = Opposite ÷ Hypotenuse
:Cosine = Adjacent ÷ Hypotenuse
:Tangent = Opposite ÷ Adjacent
One way to remember the letters is to sound them out phonetically (i.e. , similar to Krakatoa
Krakatoa (), also transcribed (), is a caldera in the Sunda Strait between the islands of Java and Sumatra in the Indonesian province of Lampung. The caldera is part of a volcanic island group ( Krakatoa archipelago) comprising four islands. T ...
). Another method is to expand the letters into a sentence, such as "Some Old Hippie Caught Another Hippie Trippin' On Acid".
The unit circle and common trigonometric values

Trigonometric functions of real or complex variables
Using the unit circle, one can extend the definitions of trigonometric ratios to all positive and negative arguments (seetrigonometric function
In mathematics, the trigonometric functions (also called circular functions, angle functions or goniometric functions) are real functions which relate an angle of a right-angled triangle to ratios of two side lengths. They are widely used in a ...
).
Graphs of trigonometric functions
The following table summarizes the properties of the graphs of the six main trigonometric functions:Inverse trigonometric functions
Because the six main trigonometric functions are periodic, they are not injective (or, 1 to 1), and thus are not invertible. By restricting the domain of a trigonometric function, however, they can be made invertible. The names of the inverse trigonometric functions, together with their domains and range, can be found in the following table:Power series representations
When considered as functions of a real variable, the trigonometric ratios can be represented by aninfinite series
In mathematics, a series is, roughly speaking, a description of the operation of adding infinitely many quantities, one after the other, to a given starting quantity. The study of series is a major part of calculus and its generalization, math ...
. For instance, sine and cosine have the following representations:
:
:
With these definitions the trigonometric functions can be defined for complex number
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the fo ...
s. When extended as functions of real or complex variables, the following formula holds for the complex exponential:
:
This complex exponential function, written in terms of trigonometric functions, is particularly useful.
Calculating trigonometric functions
Trigonometric functions were among the earliest uses for mathematical tables. Such tables were incorporated into mathematics textbooks and students were taught to look up values and how to interpolate between the values listed to get higher accuracy.Slide rule
The slide rule is a mechanical analog computer which is used primarily for multiplication and division, and for functions such as exponents, roots, logarithms, and trigonometry. It is not typically designed for addition or subtraction, which ...
s had special scales for trigonometric functions.
Scientific calculator
A scientific calculator is an electronic calculator, either desktop or handheld, designed to perform mathematical operations. They have completely replaced slide rules and are used in both educational and professional settings.
In some are ...
s have buttons for calculating the main trigonometric functions (sin, cos, tan, and sometimes cis and their inverses). Most allow a choice of angle measurement methods: degrees, radians, and sometimes gradians. Most computer programming language
A programming language is a system of notation for writing computer programs. Most programming languages are text-based formal languages, but they may also be graphical. They are a kind of computer language.
The description of a programming ...
s provide function libraries that include the trigonometric functions. The floating point unit
Floating may refer to:
* a type of dental work performed on horse teeth
* use of an isolation tank
* the guitar-playing technique where chords are sustained rather than scratched
* ''Floating'' (play), by Hugh Hughes
* Floating (psychological ...
hardware incorporated into the microprocessor chips used in most personal computers has built-in instructions for calculating trigonometric functions.
Other trigonometric functions
In addition to the six ratios listed earlier, there are additional trigonometric functions that were historically important, though seldom used today. These include the chord (), theversine
The versine or versed sine is a trigonometric function found in some of the earliest (Sanskrit ''Aryabhatia'',coversine
The versine or versed sine is a trigonometric function found in some of the earliest (Sanskrit ''Aryabhatia'',haversine
The versine or versed sine is a trigonometric function found in some of the earliest (Sanskrit ''Aryabhatia'',exsecant
The exsecant (exsec, exs) and excosecant (excosec, excsc, exc) are trigonometric functions defined in terms of the secant and cosecant functions. They used to be important in fields such as surveying, railway engineering, civil engineering, astro ...
(), and the excosecant
The exsecant (exsec, exs) and excosecant (excosec, excsc, exc) are trigonometric functions defined in terms of the secant (trigonometry), secant and cosecant functions. They used to be important in fields such as surveying, railway engineering, ci ...
(). See List of trigonometric identities
In trigonometry, trigonometric identities are equalities that involve trigonometric functions and are true for every value of the occurring variables for which both sides of the equality are defined. Geometrically, these are identities involvin ...
for more relations between these functions.
Applications
Astronomy
For centuries, spherical trigonometry has been used for locating solar, lunar, and stellar positions, predicting eclipses, and describing the orbits of the planets. In modern times, the technique of triangulation is used inastronomy
Astronomy () is a natural science that studies celestial objects and phenomena. It uses mathematics, physics, and chemistry in order to explain their origin and evolution. Objects of interest include planets, moons, stars, nebulae, g ...
to measure the distance to nearby stars, as well as in satellite navigation systems.
Navigation
 Historically, trigonometry has been used for locating latitudes and longitudes of sailing vessels, plotting courses, and calculating distances during navigation.
Trigonometry is still used in navigation through such means as the
Historically, trigonometry has been used for locating latitudes and longitudes of sailing vessels, plotting courses, and calculating distances during navigation.
Trigonometry is still used in navigation through such means as the Global Positioning System
The Global Positioning System (GPS), originally Navstar GPS, is a satellite-based radionavigation system owned by the United States government and operated by the United States Space Force. It is one of the global navigation satellite sy ...
and artificial intelligence
Artificial intelligence (AI) is intelligence—perceiving, synthesizing, and inferring information—demonstrated by machines, as opposed to intelligence displayed by animals and humans. Example tasks in which this is done include speech r ...
for autonomous vehicles.
Surveying
In land surveying, trigonometry is used in the calculation of lengths, areas, and relative angles between objects. On a larger scale, trigonometry is used ingeography
Geography (from Greek: , ''geographia''. Combination of Greek words ‘Geo’ (The Earth) and ‘Graphien’ (to describe), literally "earth description") is a field of science devoted to the study of the lands, features, inhabitants, an ...
to measure distances between landmarks.
Periodic functions
 The sine and cosine functions are fundamental to the theory of periodic functions, such as those that describe sound and
The sine and cosine functions are fundamental to the theory of periodic functions, such as those that describe sound and light
Light or visible light is electromagnetic radiation that can be perceived by the human eye. Visible light is usually defined as having wavelengths in the range of 400–700 nanometres (nm), corresponding to frequencies of 750–420 te ...
waves. Fourier discovered that every continuous, periodic function could be described as an infinite sum
In mathematics, a series is, roughly speaking, a description of the operation of adding infinitely many quantities, one after the other, to a given starting quantity. The study of series is a major part of calculus and its generalization, math ...
of trigonometric functions.
Even non-periodic functions can be represented as an integral
In mathematics, an integral assigns numbers to functions in a way that describes displacement, area, volume, and other concepts that arise by combining infinitesimal data. The process of finding integrals is called integration. Along wit ...
of sines and cosines through the Fourier transform. This has applications to quantum mechanics
Quantum mechanics is a fundamental theory in physics that provides a description of the physical properties of nature at the scale of atoms and subatomic particles. It is the foundation of all quantum physics including quantum chemistr ...
and communication
Communication (from la, communicare, meaning "to share" or "to be in relation with") is usually defined as the transmission of information. The term may also refer to the message communicated through such transmissions or the field of inqui ...
s, among other fields.
Optics and acoustics
Trigonometry is useful in many physical sciences, including acoustics, andoptics
Optics is the branch of physics that studies the behaviour and properties of light, including its interactions with matter and the construction of instruments that use or detect it. Optics usually describes the behaviour of visible, ultrav ...
. In these areas, they are used to describe sound
In physics, sound is a vibration that propagates as an acoustic wave, through a transmission medium such as a gas, liquid or solid.
In human physiology and psychology, sound is the ''reception'' of such waves and their ''perception'' b ...
and light waves, and to solve boundary- and transmission-related problems.
Other applications
Other fields that use trigonometry or trigonometric functions include music theory, geodesy, audio synthesis,architecture
Architecture is the art and technique of designing and building, as distinguished from the skills associated with construction. It is both the process and the product of sketching, conceiving, planning, designing, and constructing building ...
, electronics
The field of electronics is a branch of physics and electrical engineering that deals with the emission, behaviour and effects of electrons using electronic devices. Electronics uses active devices to control electron flow by amplification ...
, biology
Biology is the scientific study of life. It is a natural science with a broad scope but has several unifying themes that tie it together as a single, coherent field. For instance, all organisms are made up of cells that process hereditary i ...
, medical imaging ( CT scans and ultrasound), chemistry, number theory
Number theory (or arithmetic or higher arithmetic in older usage) is a branch of pure mathematics devoted primarily to the study of the integers and integer-valued functions. German mathematician Carl Friedrich Gauss (1777–1855) said, "Mat ...
(and hence cryptology
Cryptography, or cryptology (from grc, , translit=kryptós "hidden, secret"; and ''graphein'', "to write", or ''-logia'', "study", respectively), is the practice and study of techniques for secure communication in the presence of adver ...
), seismology
Seismology (; from Ancient Greek σεισμός (''seismós'') meaning "earthquake" and -λογία (''-logía'') meaning "study of") is the scientific study of earthquakes and the propagation of elastic waves through the Earth or through other ...
, meteorology, oceanography, image compression, phonetics
Phonetics is a branch of linguistics that studies how humans produce and perceive sounds, or in the case of sign languages, the equivalent aspects of sign. Linguists who specialize in studying the physical properties of speech are phoneticians. ...
, economics
Economics () is the social science that studies the production, distribution, and consumption of goods and services.
Economics focuses on the behaviour and interactions of economic agents and how economies work. Microeconomics analyzes ...
, electrical engineering, mechanical engineering
Mechanical engineering is the study of physical machines that may involve force and movement. It is an engineering branch that combines engineering physics and mathematics principles with materials science, to design, analyze, manufacture, an ...
, civil engineering
Civil engineering is a professional engineering discipline that deals with the design, construction, and maintenance of the physical and naturally built environment, including public works such as roads, bridges, canals, dams, airports, sewa ...
, computer graphics
Computer graphics deals with generating images with the aid of computers. Today, computer graphics is a core technology in digital photography, film, video games, cell phone and computer displays, and many specialized applications. A great de ...
, cartography
Cartography (; from grc, χάρτης , "papyrus, sheet of paper, map"; and , "write") is the study and practice of making and using maps. Combining science, aesthetics and technique, cartography builds on the premise that reality (or an i ...
, crystallography and game development
Video game development (or gamedev) is the process of developing a video game. The effort is undertaken by a developer, ranging from a single person to an international team dispersed across the globe. Development of traditional commercial PC ...
.
Identities
 Trigonometry has been noted for its many identities, that is, equations that are true for all possible inputs.
Identities involving only angles are known as ''trigonometric identities''. Other equations, known as ''triangle identities'', relate both the sides and angles of a given triangle.
Trigonometry has been noted for its many identities, that is, equations that are true for all possible inputs.
Identities involving only angles are known as ''trigonometric identities''. Other equations, known as ''triangle identities'', relate both the sides and angles of a given triangle.
Triangle identities
In the following identities, ''A'', ''B'' and ''C'' are the angles of a triangle and ''a'', ''b'' and ''c'' are the lengths of sides of the triangle opposite the respective angles (as shown in the diagram).Law of sines
Thelaw of sines
In trigonometry, the law of sines, sine law, sine formula, or sine rule is an equation relating the lengths of the sides of any triangle to the sines of its angles. According to the law,
\frac \,=\, \frac \,=\, \frac \,=\, 2R,
where , and ar ...
(also known as the "sine rule") for an arbitrary triangle states:
:
where is the area of the triangle and ''R'' is the radius of the circumscribed circle
In geometry, the circumscribed circle or circumcircle of a polygon is a circle that passes through all the vertices of the polygon. The center of this circle is called the circumcenter and its radius is called the circumradius.
Not every polyg ...
of the triangle:
:
Law of cosines
Thelaw of cosines
In trigonometry, the law of cosines (also known as the cosine formula, cosine rule, or al-Kashi's theorem) relates the lengths of the sides of a triangle to the cosine of one of its angles. Using notation as in Fig. 1, the law of cosines states ...
(known as the cosine formula, or the "cos rule") is an extension of the Pythagorean theorem to arbitrary triangles:
:
or equivalently:
:
Law of tangents
The law of tangents, developed byFrançois Viète
François Viète, Seigneur de la Bigotière ( la, Franciscus Vieta; 1540 – 23 February 1603), commonly know by his mononym, Vieta, was a French mathematician whose work on new algebra was an important step towards modern algebra, due to i ...
, is an alternative to the Law of Cosines when solving for the unknown edges of a triangle, providing simpler computations when using trigonometric tables. It is given by:
:
Area
Given two sides ''a'' and ''b'' and the angle between the sides ''C'', the area of the triangle is given by half the product of the lengths of two sides and the sine of the angle between the two sides: :Heron's formula
In geometry, Heron's formula (or Hero's formula) gives the area of a triangle in terms of the three side lengths , , . If s = \tfrac12(a + b + c) is the semiperimeter of the triangle, the area is,
:A = \sqrt.
It is named after first-century ...
is another method that may be used to calculate the area of a triangle. This formula states that if a triangle has sides of lengths ''a'', ''b'', and ''c'', and if the semiperimeter is
:
then the area of the triangle is:
:,
where R is the radius of the circumcircle
In geometry, the circumscribed circle or circumcircle of a polygon is a circle that passes through all the vertices of the polygon. The center of this circle is called the circumcenter and its radius is called the circumradius.
Not every polyg ...
of the triangle.
Trigonometric identities
Pythagorean identities
The following trigonometric identities are related to the Pythagorean theorem and hold for any value:/ref> : : : The second and third equations are derived from dividing the first equation by and , respectively.
Euler's formula
Euler's formula, which states that , produces the following analytical identities for sine, cosine, and tangent in terms of '' e'' and theimaginary unit
The imaginary unit or unit imaginary number () is a solution to the quadratic equation x^2+1=0. Although there is no real number with this property, can be used to extend the real numbers to what are called complex numbers, using addition an ...
''i'':
:
Other trigonometric identities
Other commonly used trigonometric identities include the half-angle identities, the angle sum and difference identities, and the product-to-sum identities.See also
* Aryabhata's sine table * Generalized trigonometry * Lénárt sphere *List of triangle topics
This list of triangle topics includes things related to the geometric shape, either abstractly, as in idealizations studied by geometers, or in triangular arrays such as Pascal's triangle or triangular matrices, or concretely in physical space. It ...
* List of trigonometric identities
In trigonometry, trigonometric identities are equalities that involve trigonometric functions and are true for every value of the occurring variables for which both sides of the equality are defined. Geometrically, these are identities involvin ...
* Rational trigonometry
* Skinny triangle
In trigonometry, a skinny triangle is a triangle whose height is much greater than its base. The solution of triangles, solution of such triangles can be greatly simplified by using the approximation that the sine of a small angle is equal to that ...
* Small-angle approximation
The small-angle approximations can be used to approximate the values of the main trigonometric functions, provided that the angle in question is small and is measured in radians:
:
\begin
\sin \theta &\approx \theta \\
\cos \theta &\approx 1 - \ ...
* Trigonometric functions
* Unit circle
* Uses of trigonometry
References
Bibliography
* * *Further reading
* * Linton, Christopher M. (2004). ''From Eudoxus to Einstein: A History of Mathematical Astronomy''. Cambridge University Press. *External links
Khan Academy: Trigonometry, free online micro lectures
by Alfred Monroe Kenyon and Louis Ingold, The Macmillan Company, 1914. In images, full text presented.
Benjamin Banneker's Trigonometry Puzzle
a
Convergence
Dave's Short Course in Trigonometry
by David Joyce of Clark University
Trigonometry, by Michael Corral, Covers elementary trigonometry, Distributed under GNU Free Documentation License
{{Authority control