radar on:
[Wikipedia]
[Google]
[Amazon]
Radar is a detection system that uses
 Before the
Before the  In 1935, Watson-Watt was asked to judge recent reports of a German radio-based death ray and turned the request over to Wilkins. Wilkins returned a set of calculations demonstrating the system was basically impossible. When Watson-Watt then asked what such a system might do, Wilkins recalled the earlier report about aircraft causing radio interference. This revelation led to the Daventry Experiment of 26 February 1935, using a powerful BBC shortwave transmitter as the source and their GPO receiver setup in a field while a bomber flew around the site. When the plane was clearly detected, Hugh Dowding, the Air Member for Supply and Research was very impressed with their system's potential and funds were immediately provided for further operational development. Watson-Watt's team patented the device in GB593017.
In 1935, Watson-Watt was asked to judge recent reports of a German radio-based death ray and turned the request over to Wilkins. Wilkins returned a set of calculations demonstrating the system was basically impossible. When Watson-Watt then asked what such a system might do, Wilkins recalled the earlier report about aircraft causing radio interference. This revelation led to the Daventry Experiment of 26 February 1935, using a powerful BBC shortwave transmitter as the source and their GPO receiver setup in a field while a bomber flew around the site. When the plane was clearly detected, Hugh Dowding, the Air Member for Supply and Research was very impressed with their system's potential and funds were immediately provided for further operational development. Watson-Watt's team patented the device in GB593017.

 Development of radar greatly expanded on 1 September 1936, when Watson-Watt became superintendent of a new establishment under the British
Development of radar greatly expanded on 1 September 1936, when Watson-Watt became superintendent of a new establishment under the British
 The information provided by radar includes the bearing and range (and therefore position) of the object from the radar scanner. It is thus used in many different fields where the need for such positioning is crucial. The first use of radar was for military purposes: to locate air, ground and sea targets. This evolved in the civilian field into applications for aircraft, ships, and automobiles.
In
The information provided by radar includes the bearing and range (and therefore position) of the object from the radar scanner. It is thus used in many different fields where the need for such positioning is crucial. The first use of radar was for military purposes: to locate air, ground and sea targets. This evolved in the civilian field into applications for aircraft, ships, and automobiles.
In
 A radar system has a
A radar system has a
 If
If
 Frequency shift is caused by motion that changes the number of wavelengths between the reflector and the radar. This can degrade or enhance radar performance depending upon how it affects the detection process. As an example,
Frequency shift is caused by motion that changes the number of wavelengths between the reflector and the radar. This can degrade or enhance radar performance depending upon how it affects the detection process. As an example,
 A radar beam follows a linear path in vacuum but follows a somewhat curved path in atmosphere due to variation in the
A radar beam follows a linear path in vacuum but follows a somewhat curved path in atmosphere due to variation in the
 Clutter may also originate from multipath echoes from valid targets caused by ground reflection,
Clutter may also originate from multipath echoes from valid targets caused by ground reflection,
 One way to obtain a distance measurement (ranging) is based on the time-of-flight: transmit a short pulse of radio signal (electromagnetic radiation) and measure the time it takes for the reflection to return. The distance is one-half the round trip time multiplied by the speed of the signal. The factor of one-half comes from the fact that the signal has to travel to the object and back again. Since radio waves travel at the
One way to obtain a distance measurement (ranging) is based on the time-of-flight: transmit a short pulse of radio signal (electromagnetic radiation) and measure the time it takes for the reflection to return. The distance is one-half the round trip time multiplied by the speed of the signal. The factor of one-half comes from the fact that the signal has to travel to the object and back again. Since radio waves travel at the
 Another form of distance measuring radar is based on frequency modulation. In these systems, the frequency of the transmitted signal is changed over time. Since the signal takes a finite time to travel to and from the target, the received signal is a different frequency than what the transmitter is broadcasting at the time the reflected signal arrives back at the radar. By comparing the frequency of the two signals the difference can be easily measured. This is easily accomplished with very high accuracy even in 1940s electronics. A further advantage is that the radar can operate effectively at relatively low frequencies. This was important in the early development of this type when high-frequency signal generation was difficult or expensive.
This technique can be used in continuous wave radar and is often found in aircraft
Another form of distance measuring radar is based on frequency modulation. In these systems, the frequency of the transmitted signal is changed over time. Since the signal takes a finite time to travel to and from the target, the received signal is a different frequency than what the transmitter is broadcasting at the time the reflected signal arrives back at the radar. By comparing the frequency of the two signals the difference can be easily measured. This is easily accomplished with very high accuracy even in 1940s electronics. A further advantage is that the radar can operate effectively at relatively low frequencies. This was important in the early development of this type when high-frequency signal generation was difficult or expensive.
This technique can be used in continuous wave radar and is often found in aircraft
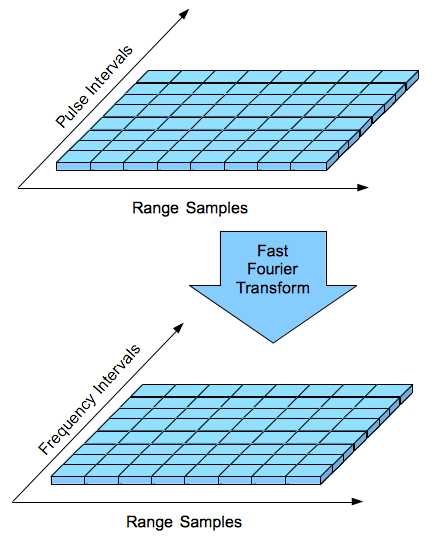 Pulse-Doppler signal processing includes frequency filtering in the detection process. The space between each transmit pulse is divided into range cells or range gates. Each cell is filtered independently much like the process used by a
Pulse-Doppler signal processing includes frequency filtering in the detection process. The space between each transmit pulse is divided into range cells or range gates. Each cell is filtered independently much like the process used by a
 A radar's components are:
* A
A radar's components are:
* A
 Radio signals broadcast from a single antenna will spread out in all directions, and likewise a single antenna will receive signals equally from all directions. This leaves the radar with the problem of deciding where the target object is located.
Early systems tended to use omnidirectional broadcast antennas, with directional receiver antennas which were pointed in various directions. For instance, the first system to be deployed, Chain Home, used two straight antennas at
Radio signals broadcast from a single antenna will spread out in all directions, and likewise a single antenna will receive signals equally from all directions. This leaves the radar with the problem of deciding where the target object is located.
Early systems tended to use omnidirectional broadcast antennas, with directional receiver antennas which were pointed in various directions. For instance, the first system to be deployed, Chain Home, used two straight antennas at
 More modern systems use a steerable parabolic "dish" to create a tight broadcast beam, typically using the same dish as the receiver. Such systems often combine two radar frequencies in the same antenna in order to allow automatic steering, or ''radar lock''.
Parabolic reflectors can be either symmetric parabolas or spoiled parabolas:
Symmetric parabolic antennas produce a narrow "pencil" beam in both the X and Y dimensions and consequently have a higher gain. The NEXRAD Pulse-Doppler weather radar uses a symmetric antenna to perform detailed volumetric scans of the atmosphere. Spoiled parabolic antennas produce a narrow beam in one dimension and a relatively wide beam in the other. This feature is useful if target detection over a wide range of angles is more important than target location in three dimensions. Most 2D surveillance radars use a spoiled parabolic antenna with a narrow azimuthal beamwidth and wide vertical beamwidth. This beam configuration allows the radar operator to detect an aircraft at a specific azimuth but at an indeterminate height. Conversely, so-called "nodder" height finding radars use a dish with a narrow vertical beamwidth and wide azimuthal beamwidth to detect an aircraft at a specific height but with low azimuthal precision.
More modern systems use a steerable parabolic "dish" to create a tight broadcast beam, typically using the same dish as the receiver. Such systems often combine two radar frequencies in the same antenna in order to allow automatic steering, or ''radar lock''.
Parabolic reflectors can be either symmetric parabolas or spoiled parabolas:
Symmetric parabolic antennas produce a narrow "pencil" beam in both the X and Y dimensions and consequently have a higher gain. The NEXRAD Pulse-Doppler weather radar uses a symmetric antenna to perform detailed volumetric scans of the atmosphere. Spoiled parabolic antennas produce a narrow beam in one dimension and a relatively wide beam in the other. This feature is useful if target detection over a wide range of angles is more important than target location in three dimensions. Most 2D surveillance radars use a spoiled parabolic antenna with a narrow azimuthal beamwidth and wide vertical beamwidth. This beam configuration allows the radar operator to detect an aircraft at a specific azimuth but at an indeterminate height. Conversely, so-called "nodder" height finding radars use a dish with a narrow vertical beamwidth and wide azimuthal beamwidth to detect an aircraft at a specific height but with low azimuthal precision.
 Applied similarly to the parabolic reflector, the slotted waveguide is moved mechanically to scan and is particularly suitable for non-tracking surface scan systems, where the vertical pattern may remain constant. Owing to its lower cost and less wind exposure, shipboard, airport surface, and harbour surveillance radars now use this approach in preference to a parabolic antenna.
Applied similarly to the parabolic reflector, the slotted waveguide is moved mechanically to scan and is particularly suitable for non-tracking surface scan systems, where the vertical pattern may remain constant. Owing to its lower cost and less wind exposure, shipboard, airport surface, and harbour surveillance radars now use this approach in preference to a parabolic antenna.
 Another method of steering is used in a
Another method of steering is used in a
All you ever wanted to know about British air defence radar
'". The Radar Pages. (History and details of various British radar systems) * Buderi, "
'". Privateline.com. (Anecdotal account of the carriage of the world's first high power cavity magnetron from Britain to the US during WW2.) * Ekco Rada
WW2 Shadow Factory
The secret development of British radar. * ES31
* Hollmann, Martin, "
'"
Radar World
* Penley, Bill, and Jonathan Penley, "
��an Introduction''". 2002. * Pub 1310 ''Radar Navigation and Maneuvering Board Manual'', National Imagery and Mapping Agency, Bethesda, MD 2001 (US govt publication '...intended to be used primarily as a manual of instruction in navigation schools and by naval and merchant marine personnel.') * Wesley Stout, 194
Early development and production by Chrysler Corp. during WWII. * Swords, Seán S., "Technical History of the Beginnings of Radar", '' IEE History of Technology Series'', Vol. 6, London: Peter Peregrinus, 1986
MIT Video Course: Introduction to Radar Systems
A set of 10 video lectures developed at Lincoln Laboratory to develop an understanding of radar systems and technologies.
Glossary of radar terminology
{{Authority control Avionics Aircraft instruments Microwave technology Measuring instruments Navigational equipment Air traffic control Science and technology during World War II Targeting (warfare) Radio stations and systems ITU 1940s neologisms Wireless communication systems
radio wave
Radio waves are a type of electromagnetic radiation with the longest wavelengths in the electromagnetic spectrum, typically with frequencies of 300 gigahertz ( GHz) and below. At 300 GHz, the corresponding wavelength is 1 mm (sho ...
s to determine the distance ('' ranging''), angle, and radial velocity
The radial velocity or line-of-sight velocity, also known as radial speed or range rate, of a target with respect to an observer is the rate of change of the distance or range between the two points. It is equivalent to the vector projection ...
of objects relative to the site. It can be used to detect aircraft
An aircraft is a vehicle that is able to flight, fly by gaining support from the Atmosphere of Earth, air. It counters the force of gravity by using either Buoyancy, static lift or by using the Lift (force), dynamic lift of an airfoil, or in ...
, ships
A ship is a large watercraft that travels the world's oceans and other sufficiently deep waterways, carrying cargo or passengers, or in support of specialized missions, such as defense, research, and fishing. Ships are generally distinguished ...
, spacecraft
A spacecraft is a vehicle or machine designed to fly in outer space. A type of artificial satellite, spacecraft are used for a variety of purposes, including communications, Earth observation, meteorology, navigation, space colonization, ...
, guided missiles, motor vehicle
A motor vehicle, also known as motorized vehicle or automotive vehicle, is a self-propelled land vehicle, commonly wheeled, that does not operate on rails (such as trains or trams) and is used for the transportation of people or cargo.
The ...
s, weather formations, and terrain
Terrain or relief (also topographical relief) involves the vertical and horizontal dimensions of land surface. The term bathymetry is used to describe underwater relief, while hypsometry studies terrain relative to sea level. The Latin word ...
. A radar system consists of a transmitter
In electronics and telecommunications, a radio transmitter or just transmitter is an electronic device which produces radio waves with an antenna. The transmitter itself generates a radio frequency alternating current, which is applied to the ...
producing electromagnetic wave
In physics, electromagnetic radiation (EMR) consists of waves of the electromagnetic (EM) field, which propagate through space and carry momentum and electromagnetic radiant energy. It includes radio waves, microwaves, infrared, (visible) ...
s in the radio
Radio is the technology of signaling and communicating using radio waves. Radio waves are electromagnetic waves of frequency between 30 hertz (Hz) and 300 gigahertz (GHz). They are generated by an electronic device called a tr ...
or microwave
Microwave is a form of electromagnetic radiation with wavelengths ranging from about one meter to one millimeter corresponding to frequencies between 300 MHz and 300 GHz respectively. Different sources define different frequency ra ...
s domain, a transmitting antenna
Antenna ( antennas or antennae) may refer to:
Science and engineering
* Antenna (radio), also known as an aerial, a transducer designed to transmit or receive electromagnetic (e.g., TV or radio) waves
* Antennae Galaxies, the name of two collid ...
, a receiving antenna (often the same antenna is used for transmitting and receiving) and a receiver and processor
Processor may refer to:
Computing Hardware
* Processor (computing)
**Central processing unit (CPU), the hardware within a computer that executes a program
*** Microprocessor, a central processing unit contained on a single integrated circuit (I ...
to determine properties of the objects. Radio waves (pulsed or continuous) from the transmitter reflect off the objects and return to the receiver, giving information about the objects' locations and speeds.
Radar was developed secretly for military
A military, also known collectively as armed forces, is a heavily armed, highly organized force primarily intended for warfare. It is typically authorized and maintained by a sovereign state, with its members identifiable by their distinct ...
use by several countries in the period before and during World War II
World War II or the Second World War, often abbreviated as WWII or WW2, was a world war that lasted from 1939 to 1945. It involved the World War II by country, vast majority of the world's countries—including all of the great power ...
. A key development was the cavity magnetron in the United Kingdom
The United Kingdom of Great Britain and Northern Ireland, commonly known as the United Kingdom (UK) or Britain, is a country in Europe, off the north-western coast of the continental mainland. It comprises England, Scotland, Wales and ...
, which allowed the creation of relatively small systems with sub-meter resolution. The term ''RADAR'' was coined in 1940 by the United States Navy
The United States Navy (USN) is the maritime service branch of the United States Armed Forces and one of the eight uniformed services of the United States. It is the largest and most powerful navy in the world, with the estimated tonnage ...
as an acronym
An acronym is a word or name formed from the initial components of a longer name or phrase. Acronyms are usually formed from the initial letters of words, as in ''NATO'' (''North Atlantic Treaty Organization''), but sometimes use syllables, as ...
for radio detection and ranging. The term ''radar'' has since entered English and other languages as a common noun, losing all capitalization.
The modern uses of radar are highly diverse, including air and terrestrial traffic control, radar astronomy
Radar astronomy is a technique of observing nearby astronomical objects by reflecting radio waves or microwaves off target objects and analyzing their reflections. Radar astronomy differs from '' radio astronomy'' in that the latter is a passive o ...
, air-defense systems, anti-missile systems, marine radar
Marine radars are X band or S band radars on ships, used to detect other ships and land obstacles, to provide bearing and distance for collision avoidance and navigation at sea. They are electronic navigation instruments that use a rotatin ...
s to locate landmarks and other ships, aircraft anti-collision systems, ocean surveillance systems, outer space surveillance
Space domain awareness is the study and monitoring of satellites orbiting the earth. It involves the detection, tracking, cataloging and identification of artificial objects, i.e. active/inactive satellites, spent rocket bodies, or Space debris, ...
and rendezvous systems, meteorological
Meteorology is a branch of the atmospheric sciences (which include atmospheric chemistry and physics) with a major focus on weather forecasting. The study of meteorology dates back millennia, though significant progress in meteorology did not ...
precipitation monitoring, altimetry and flight control system
A conventional fixed-wing aircraft flight control system consists of flight control surfaces, the respective cockpit controls, connecting linkages, and the necessary operating mechanisms to control an aircraft's direction in flight. Aircraft ...
s, guided missile
In military terminology, a missile is a guided airborne ranged weapon capable of self-propelled flight usually by a jet engine or rocket motor. Missiles are thus also called guided missiles or guided rockets (when a previously unguided rocket ...
target locating systems, self-driving cars, and ground-penetrating radar
Ground-penetrating radar (GPR) is a Geophysics, geophysical method that uses radar pulses to Geophysical imaging, image the subsurface. It is a non-intrusive method of surveying the sub-surface to investigate underground utilities such as concrete, ...
for geological observations. High tech radar systems are associated with digital signal processing
Digital signal processing (DSP) is the use of digital processing, such as by computers or more specialized digital signal processors, to perform a wide variety of signal processing operations. The digital signals processed in this manner are ...
, machine learning
Machine learning (ML) is a field of inquiry devoted to understanding and building methods that 'learn', that is, methods that leverage data to improve performance on some set of tasks. It is seen as a part of artificial intelligence.
Machine ...
and are capable of extracting useful information from very high noise
Noise is unwanted sound considered unpleasant, loud or disruptive to hearing. From a physics standpoint, there is no distinction between noise and desired sound, as both are vibrations through a medium, such as air or water. The difference aris ...
levels.
Other systems similar to radar make use of other parts of the electromagnetic spectrum
The electromagnetic spectrum is the range of frequencies (the spectrum) of electromagnetic radiation and their respective wavelengths and photon energies.
The electromagnetic spectrum covers electromagnetic waves with frequencies ranging fro ...
. One example is lidar
Lidar (, also LIDAR, or LiDAR; sometimes LADAR) is a method for determining ranges (variable distance) by targeting an object or a surface with a laser and measuring the time for the reflected light to return to the receiver. It can also be ...
, which uses predominantly infrared light from laser
A laser is a device that emits light through a process of optical amplification based on the stimulated emission of electromagnetic radiation. The word "laser" is an acronym for "light amplification by stimulated emission of radiation". The ...
s rather than radio waves. With the emergence of driver-less vehicles, radar is expected to assist the automated platform to monitor its environment, thus preventing unwanted incidents.
History
First experiments
As early as 1886, German physicistHeinrich Hertz
Heinrich Rudolf Hertz ( ; ; 22 February 1857 – 1 January 1894) was a German physicist who first conclusively proved the existence of the electromagnetic waves predicted by James Clerk Maxwell's equations of electromagnetism. The uni ...
showed that radio waves could be reflected from solid objects. In 1895, Alexander Popov, a physics instructor at the Imperial Russian Navy
The Imperial Russian Navy () operated as the navy of the Russian Tsardom and later the Russian Empire from 1696 to 1917. Formally established in 1696, it lasted until dissolved in the wake of the February Revolution of 1917. It developed from ...
school in Kronstadt
Kronstadt (russian: Кроншта́дт, Kronshtadt ), also spelled Kronshtadt, Cronstadt or Kronštádt (from german: link=no, Krone for " crown" and ''Stadt'' for "city") is a Russian port city in Kronshtadtsky District of the federal city ...
, developed an apparatus using a coherer
The coherer was a primitive form of radio signal detector used in the first radio receivers during the wireless telegraphy era at the beginning of the 20th century. Its use in radio was based on the 1890 findings of French physicist Édouard Bran ...
tube for detecting distant lightning strikes. The next year, he added a spark-gap transmitter
A spark-gap transmitter is an obsolete type of transmitter, radio transmitter which generates radio waves by means of an electric spark."Radio Transmitters, Early" in Spark-gap transmitters were the first type of radio transmitter, and were the m ...
. In 1897, while testing this equipment for communicating between two ships in the Baltic Sea
The Baltic Sea is an arm of the Atlantic Ocean that is enclosed by Denmark, Estonia, Finland, Germany, Latvia, Lithuania, Poland, Russia, Sweden and the North and Central European Plain.
The sea stretches from 53°N to 66°N latitude and from ...
, he took note of an interference beat caused by the passage of a third vessel. In his report, Popov wrote that this phenomenon might be used for detecting objects, but he did nothing more with this observation.
The German inventor Christian Hülsmeyer was the first to use radio waves to detect "the presence of distant metallic objects". In 1904, he demonstrated the feasibility of detecting a ship in dense fog, but not its distance from the transmitter. He obtained a patent for his detection device in April 1904 and later a patent for a related amendment for estimating the distance to the ship. He also obtained a British patent on 23 September 1904 for a full radar system, that he called a ''telemobiloscope''. It operated on a 50 cm wavelength and the pulsed radar signal was created via a spark-gap. His system already used the classic antenna setup of horn antenna with parabolic reflector and was presented to German military officials in practical tests in Cologne
Cologne ( ; german: Köln ; ksh, Kölle ) is the largest city of the German western state of North Rhine-Westphalia (NRW) and the fourth-most populous city of Germany with 1.1 million inhabitants in the city proper and 3.6 millio ...
and Rotterdam
Rotterdam ( , , , lit. ''The Dam on the River Rotte (river), Rotte'') is the second largest List of cities in the Netherlands by province, city and List of municipalities of the Netherlands, municipality in the Netherlands. It is in the Prov ...
harbour but was rejected.
In 1915, Robert Watson-Watt
Sir Robert Alexander Watson Watt (13 April 1892 – 5 December 1973) was a Scottish pioneer of radio direction finding and radar technology.
Watt began his career in radio physics with a job at the Met Office, where he began looking for accura ...
used radio technology to provide advance warning to airmen and during the 1920s went on to lead the U.K. research establishment to make many advances using radio techniques, including the probing of the ionosphere
The ionosphere () is the ionized part of the upper atmosphere of Earth, from about to above sea level, a region that includes the thermosphere and parts of the mesosphere and exosphere. The ionosphere is ionized by solar radiation. It plays ...
and the detection of lightning
Lightning is a naturally occurring electrostatic discharge during which two electrically charged regions, both in the atmosphere or with one on the ground, temporarily neutralize themselves, causing the instantaneous release of an average ...
at long distances. Through his lightning experiments, Watson-Watt became an expert on the use of radio direction finding
Direction finding (DF), or radio direction finding (RDF), isin accordance with International Telecommunication Union (ITU)defined as radio location that uses the reception of radio waves to determine the direction in which a radio stati ...
before turning his inquiry to shortwave
Shortwave radio is radio transmission using shortwave (SW) radio frequencies. There is no official definition of the band, but the range always includes all of the high frequency band (HF), which extends from 3 to 30 MHz (100 to 10 me ...
transmission. Requiring a suitable receiver for such studies, he told the "new boy" Arnold Frederic Wilkins
Arnold Frederic Wilkins OBE (20 February 1907 – 5 August 1985) was a pioneer in developing the use of radar. It was Arnold Wilkins who suggested to his boss, Robert Watson-Watt, that reflected radio waves might be used to detect aircraft, ...
to conduct an extensive review of available shortwave units. Wilkins would select a General Post Office
The General Post Office (GPO) was the state postal system and telecommunications carrier of the United Kingdom until 1969. Before the Acts of Union 1707, it was the postal system of the Kingdom of England, established by Charles II in 1660. ...
model after noting its manual's description of a "fading" effect (the common term for interference at the time) when aircraft flew overhead.
Across the Atlantic in 1922, after placing a transmitter and receiver on opposite sides of the Potomac River
The Potomac River () drains the Mid-Atlantic United States, flowing from the Potomac Highlands into Chesapeake Bay. It is long,U.S. Geological Survey. National Hydrography Dataset high-resolution flowline dataThe National Map. Retrieved Augu ...
, U.S. Navy researchers A. Hoyt Taylor and Leo C. Young
Leo C. Young (12 January 1891 – 16 January 1981) was an American radio engineer who had many accomplishments during a long career at the U.S. Naval Research Laboratory. Although self-educated, he was a member of a small, creative team which some ...
discovered that ships passing through the beam path caused the received signal to fade in and out. Taylor submitted a report, suggesting that this phenomenon might be used to detect the presence of ships in low visibility, but the Navy did not immediately continue the work. Eight years later, Lawrence A. Hyland at the Naval Research Laboratory
The United States Naval Research Laboratory (NRL) is the corporate research laboratory for the United States Navy and the United States Marine Corps. It was founded in 1923 and conducts basic scientific research, applied research, technologic ...
(NRL) observed similar fading effects from passing aircraft; this revelation led to a patent application as well as a proposal for further intensive research on radio-echo signals from moving targets to take place at NRL, where Taylor and Young were based at the time.
Similarly, in the UK, L. S. Alder took out a secret provisional patent for Naval radar in 1928.
W.A.S. Butement and P. E. Pollard developed a breadboard test unit, operating at 50 cm (600 MHz) and using pulsed modulation which gave successful laboratory results. In January 1931, a writeup on the apparatus was entered in the ''Inventions Book'' maintained by the Royal Engineers. This is the first official record in Great Britain of the technology that was used in coastal defence and was incorporated into Chain Home
Chain Home, or CH for short, was the codename for the ring of coastal Early Warning radar stations built by the Royal Air Force (RAF) before and during the Second World War to detect and track aircraft. Initially known as RDF, and given the of ...
as Chain Home (low).
Just before World War II
 Before the
Before the Second World War
World War II or the Second World War, often abbreviated as WWII or WW2, was a world war that lasted from 1939 to 1945. It involved the vast majority of the world's countries—including all of the great powers—forming two opposi ...
, researchers in the United Kingdom, France
France (), officially the French Republic ( ), is a country primarily located in Western Europe. It also comprises of Overseas France, overseas regions and territories in the Americas and the Atlantic Ocean, Atlantic, Pacific Ocean, Pac ...
, Germany
Germany,, officially the Federal Republic of Germany, is a country in Central Europe. It is the second most populous country in Europe after Russia, and the most populous member state of the European Union. Germany is situated betwee ...
, Italy
Italy ( it, Italia ), officially the Italian Republic, ) or the Republic of Italy, is a country in Southern Europe. It is located in the middle of the Mediterranean Sea, and its territory largely coincides with the homonymous geographical ...
, Japan
Japan ( ja, 日本, or , and formally , ''Nihonkoku'') is an island country in East Asia. It is situated in the northwest Pacific Ocean, and is bordered on the west by the Sea of Japan, while extending from the Sea of Okhotsk in the n ...
, the Netherlands, the Soviet Union
The Soviet Union,. officially the Union of Soviet Socialist Republics. (USSR),. was a transcontinental country that spanned much of Eurasia from 1922 to 1991. A flagship communist state, it was nominally a federal union of fifteen nationa ...
, and the United States, independently and in great secrecy, developed technologies that led to the modern version of radar. Australia, Canada, New Zealand, and South Africa followed prewar Great Britain's radar development, and Hungary
Hungary ( hu, Magyarország ) is a landlocked country in Central Europe. Spanning of the Carpathian Basin, it is bordered by Slovakia to the north, Ukraine to the northeast, Romania to the east and southeast, Serbia to the south, Cr ...
generated its radar technology during the war.
In France in 1934, following systematic studies on the split-anode magnetron, the research branch of the Compagnie générale de la télégraphie sans fil (CSF) headed by Maurice Ponte with Henri Gutton, Sylvain Berline and M. Hugon, began developing an obstacle-locating radio apparatus, aspects of which were installed on the ocean liner ''Normandie'' in 1935.
During the same period, Soviet military engineer P.K. Oshchepkov, in collaboration with the Leningrad Electrotechnical Institute, produced an experimental apparatus, RAPID, capable of detecting an aircraft within 3 km of a receiver. The Soviets produced their first mass production radars RUS-1 and RUS-2 Redut in 1939 but further development was slowed following the arrest of Oshchepkov and his subsequent gulag
The Gulag, an acronym for , , "chief administration of the camps". The original name given to the system of camps controlled by the State Political Directorate, GPU was the Main Administration of Corrective Labor Camps (, )., name=, group= ...
sentence. In total, only 607 Redut stations were produced during the war. The first Russian airborne radar, Gneiss-2 Gneiss-2 was the first Soviet produced airborne radar system. It was introduced in 1942, and was installed on Petlyakov Pe-2, Petlyakov Pe-3 and Douglas A-20 Havoc aircraft .
Development
During the Soviet-Finnish War, the chief of the Air Force Re ...
, entered into service in June 1943 on Pe-2
The Petlyakov Pe-2 (russian: Петляков Пе-2) was a Soviet twin-engine dive bomber used during World War II. One of the outstanding tactical attack aircraft of the war,Ethell 1996, p. 152. it also proved successful as a heavy fighter, as ...
dive bombers. More than 230 Gneiss-2 stations were produced by the end of 1944. The French and Soviet systems, however, featured continuous-wave operation that did not provide the full performance ultimately synonymous with modern radar systems.
Full radar evolved as a pulsed system, and the first such elementary apparatus was demonstrated in December 1934 by the American Robert M. Page, working at the Naval Research Laboratory
The United States Naval Research Laboratory (NRL) is the corporate research laboratory for the United States Navy and the United States Marine Corps. It was founded in 1923 and conducts basic scientific research, applied research, technologic ...
. The following year, the United States Army
The United States Army (USA) is the land service branch of the United States Armed Forces. It is one of the eight U.S. uniformed services, and is designated as the Army of the United States in the U.S. Constitution.Article II, section 2, ...
successfully tested a primitive surface-to-surface radar to aim coastal battery searchlight
A searchlight (or spotlight) is an apparatus that combines an extremely luminosity, bright source (traditionally a carbon arc lamp) with a mirrored parabolic reflector to project a powerful beam of light of approximately parallel rays in a part ...
s at night. This design was followed by a pulsed system demonstrated in May 1935 by Rudolf Kühnhold and the firm in Germany and then another in June 1935 by an Air Ministry
The Air Ministry was a department of the Government of the United Kingdom with the responsibility of managing the affairs of the Royal Air Force, that existed from 1918 to 1964. It was under the political authority of the Secretary of Stat ...
team led by Robert Watson-Watt
Sir Robert Alexander Watson Watt (13 April 1892 – 5 December 1973) was a Scottish pioneer of radio direction finding and radar technology.
Watt began his career in radio physics with a job at the Met Office, where he began looking for accura ...
in Great Britain.
 In 1935, Watson-Watt was asked to judge recent reports of a German radio-based death ray and turned the request over to Wilkins. Wilkins returned a set of calculations demonstrating the system was basically impossible. When Watson-Watt then asked what such a system might do, Wilkins recalled the earlier report about aircraft causing radio interference. This revelation led to the Daventry Experiment of 26 February 1935, using a powerful BBC shortwave transmitter as the source and their GPO receiver setup in a field while a bomber flew around the site. When the plane was clearly detected, Hugh Dowding, the Air Member for Supply and Research was very impressed with their system's potential and funds were immediately provided for further operational development. Watson-Watt's team patented the device in GB593017.
In 1935, Watson-Watt was asked to judge recent reports of a German radio-based death ray and turned the request over to Wilkins. Wilkins returned a set of calculations demonstrating the system was basically impossible. When Watson-Watt then asked what such a system might do, Wilkins recalled the earlier report about aircraft causing radio interference. This revelation led to the Daventry Experiment of 26 February 1935, using a powerful BBC shortwave transmitter as the source and their GPO receiver setup in a field while a bomber flew around the site. When the plane was clearly detected, Hugh Dowding, the Air Member for Supply and Research was very impressed with their system's potential and funds were immediately provided for further operational development. Watson-Watt's team patented the device in GB593017.

 Development of radar greatly expanded on 1 September 1936, when Watson-Watt became superintendent of a new establishment under the British
Development of radar greatly expanded on 1 September 1936, when Watson-Watt became superintendent of a new establishment under the British Air Ministry
The Air Ministry was a department of the Government of the United Kingdom with the responsibility of managing the affairs of the Royal Air Force, that existed from 1918 to 1964. It was under the political authority of the Secretary of Stat ...
, Bawdsey Research Station located in Bawdsey Manor
Bawdsey Manor stands at a prominent position at the mouth of the River Deben close to the village of Bawdsey in Suffolk, England, about northeast of London.
Built in 1886, it was enlarged in 1895 as the principal residence of Sir William C ...
, near Felixstowe, Suffolk. Work there resulted in the design and installation of aircraft detection and tracking stations called "Chain Home
Chain Home, or CH for short, was the codename for the ring of coastal Early Warning radar stations built by the Royal Air Force (RAF) before and during the Second World War to detect and track aircraft. Initially known as RDF, and given the of ...
" along the East and South coasts of England in time for the outbreak of World War II in 1939. This system provided the vital advance information that helped the Royal Air Force win the Battle of Britain
The Battle of Britain, also known as the Air Battle for England (german: die Luftschlacht um England), was a military campaign of the Second World War, in which the Royal Air Force (RAF) and the Fleet Air Arm (FAA) of the Royal Navy defende ...
; without it, significant numbers of fighter aircraft, which Great Britain did not have available, would always have needed to be in the air to respond quickly. If German-aircraft detection had relied solely on the observations of ground-based individuals, Great Britain might have lost the Battle of Britain. The radar formed part of the " Dowding system" for collecting reports of enemy aircraft and coordinating the response.
Given all required funding and development support, the team produced working radar systems in 1935 and began deployment. By 1936, the first five Chain Home (CH) systems were operational and by 1940 stretched across the entire UK including Northern Ireland. Even by standards of the era, CH was crude; instead of broadcasting and receiving from an aimed antenna, CH broadcast a signal floodlighting the entire area in front of it, and then used one of Watson-Watt's own radio direction finders to determine the direction of the returned echoes. This fact meant CH transmitters had to be much more powerful and have better antennas than competing systems but allowed its rapid introduction using existing technologies.
During World War II
A key development was the cavity magnetron in the UK, which allowed the creation of relatively small systems with sub-meter resolution. Britain shared the technology with the U.S. during the 1940Tizard Mission
The Tizard Mission, officially the British Technical and Scientific Mission, was a British delegation that visited the United States during WWII to obtain the industrial resources to exploit the military potential of the research and development ( ...
.
In April 1940, ''Popular Science
''Popular Science'' (also known as ''PopSci'') is an American digital magazine carrying popular science content, which refers to articles for the general reader on science and technology subjects. ''Popular Science'' has won over 58 awards, incl ...
'' showed an example of a radar unit using the Watson-Watt patent in an article on air defence. Also, in late 1941 ''Popular Mechanics'' had an article in which a U.S. scientist speculated about the British early warning system on the English east coast and came close to what it was and how it worked. Watson-Watt was sent to the U.S. in 1941 to advise on air defense after Japan's attack on Pearl Harbor
The attack on Pearl HarborAlso known as the Battle of Pearl Harbor was a surprise military strike by the Imperial Japanese Navy Air Service upon the United States against the naval base at Pearl Harbor in Honolulu, Territory of Hawaii ...
. Alfred Lee Loomis organized the secret MIT Radiation Laboratory at Massachusetts Institute of Technology
The Massachusetts Institute of Technology (MIT) is a private land-grant research university in Cambridge, Massachusetts. Established in 1861, MIT has played a key role in the development of modern technology and science, and is one of th ...
, Cambridge, Massachusetts which developed microwave radar technology in the years 1941–45. Later, in 1943, Page greatly improved radar with the monopulse technique that was used for many years in most radar applications.
The war precipitated research to find better resolution, more portability, and more features for radar, including complementary navigation systems like Oboe
The oboe ( ) is a type of double reed woodwind instrument. Oboes are usually made of wood, but may also be made of synthetic materials, such as plastic, resin, or hybrid composites. The most common oboe plays in the treble or soprano range.
...
used by the RAF's Pathfinder.
Applications
 The information provided by radar includes the bearing and range (and therefore position) of the object from the radar scanner. It is thus used in many different fields where the need for such positioning is crucial. The first use of radar was for military purposes: to locate air, ground and sea targets. This evolved in the civilian field into applications for aircraft, ships, and automobiles.
In
The information provided by radar includes the bearing and range (and therefore position) of the object from the radar scanner. It is thus used in many different fields where the need for such positioning is crucial. The first use of radar was for military purposes: to locate air, ground and sea targets. This evolved in the civilian field into applications for aircraft, ships, and automobiles.
In aviation
Aviation includes the activities surrounding mechanical flight and the aircraft industry. ''Aircraft'' includes airplane, fixed-wing and helicopter, rotary-wing types, morphable wings, wing-less lifting bodies, as well as aerostat, lighter- ...
, aircraft can be equipped with radar devices that warn of aircraft or other obstacles in or approaching their path, display weather information, and give accurate altitude readings. The first commercial device fitted to aircraft was a 1938 Bell Lab unit on some United Air Lines aircraft. Aircraft can land in fog at airports equipped with radar-assisted ground-controlled approach systems in which the plane's position is observed on precision approach radar
Precision approach radar (PAR) is a type of radar guidance system designed to provide lateral and vertical guidance to an aircraft pilot for landing, until the landing threshold is reached. Controllers monitoring the PAR displays observe each ai ...
screens by operators who thereby give radio landing instructions to the pilot, maintaining the aircraft on a defined approach path to the runway. Military fighter aircraft are usually fitted with air-to-air targeting radars, to detect and target enemy aircraft. In addition, larger specialized military aircraft carry powerful airborne radars to observe air traffic over a wide region and direct fighter aircraft towards targets.
Marine radar
Marine radars are X band or S band radars on ships, used to detect other ships and land obstacles, to provide bearing and distance for collision avoidance and navigation at sea. They are electronic navigation instruments that use a rotatin ...
s are used to measure the bearing and distance of ships to prevent collision with other ships, to navigate, and to fix their position at sea when within range of shore or other fixed references such as islands, buoys, and lightships. In port or in harbour, vessel traffic service radar systems are used to monitor and regulate ship movements in busy waters.
Meteorologists use radar to monitor precipitation
In meteorology, precipitation is any product of the condensation of atmospheric water vapor that falls under gravitational pull from clouds. The main forms of precipitation include drizzle, rain, sleet, snow, ice pellets, graupel and hail. ...
and wind. It has become the primary tool for short-term weather forecast
Weather forecasting is the application of science and technology to predict the conditions of the atmosphere for a given location and time. People have attempted to predict the weather informally for millennia and formally since the 19th cent ...
ing and watching for severe weather
Severe weather is any dangerous meteorological phenomenon with the potential to cause damage, serious social disruption, or loss of human life. Types of severe weather phenomena vary, depending on the latitude, altitude, topography, and atmos ...
such as thunderstorm
A thunderstorm, also known as an electrical storm or a lightning storm, is a storm characterized by the presence of lightning and its acoustic effect on the Earth's atmosphere, known as thunder. Relatively weak thunderstorms are some ...
s, tornado
A tornado is a violently rotating column of air that is in contact with both the surface of the Earth and a cumulonimbus cloud or, in rare cases, the base of a cumulus cloud. It is often referred to as a twister, whirlwind or cyclone, alt ...
es, winter storm
A winter storm is an event in which wind coincides with varieties of precipitation that only occur at freezing temperatures, such as snow, mixed snow and rain, or freezing rain. In temperate continental climates, these storms are not necessa ...
s, precipitation types, etc. Geologist
A geologist is a scientist who studies the solid, liquid, and gaseous matter that constitutes Earth and other terrestrial planets, as well as the processes that shape them. Geologists usually study geology, earth science, or geophysics, althou ...
s use specialized ground-penetrating radar
Ground-penetrating radar (GPR) is a Geophysics, geophysical method that uses radar pulses to Geophysical imaging, image the subsurface. It is a non-intrusive method of surveying the sub-surface to investigate underground utilities such as concrete, ...
s to map the composition of Earth's crust
Earth's crust is Earth's thin outer shell of rock, referring to less than 1% of Earth's radius and volume. It is the top component of the lithosphere, a division of Earth's layers that includes the crust and the upper part of the mantle. The ...
. Police forces use radar gun
A radar speed gun (also radar gun and speed trap gun) is a device used to measure the speed of moving objects. It is used in law-enforcement to measure the speed of moving vehicles and is often used in professional spectator sport, for things su ...
s to monitor vehicle speeds on the roads. Smaller radar systems are used to detect human movement. Examples are breathing pattern detection for sleep monitoring and hand and finger gesture detection for computer interaction. Automatic door opening, light activation and intruder sensing are also common.
Principles
Radar signal
 A radar system has a
A radar system has a transmitter
In electronics and telecommunications, a radio transmitter or just transmitter is an electronic device which produces radio waves with an antenna. The transmitter itself generates a radio frequency alternating current, which is applied to the ...
that emits radio wave
Radio waves are a type of electromagnetic radiation with the longest wavelengths in the electromagnetic spectrum, typically with frequencies of 300 gigahertz ( GHz) and below. At 300 GHz, the corresponding wavelength is 1 mm (sho ...
s known as ''radar signals'' in predetermined directions. When these signals contact an object they are usually reflected or scattered
Scattered may refer to:
Music
* ''Scattered'' (album), a 2010 album by The Handsome Family
* "Scattered" (The Kinks song), 1993
* "Scattered", a song by Ace Young
* "Scattered", a song by Lauren Jauregui
* "Scattered", a song by Green Day from ' ...
in many directions, although some of them will be absorbed and penetrate into the target. Radar signals are reflected especially well by materials of considerable electrical conductivity
Electrical resistivity (also called specific electrical resistance or volume resistivity) is a fundamental property of a material that measures how strongly it resists electric current. A low resistivity indicates a material that readily allows ...
—such as most metals, seawater
Seawater, or salt water, is water from a sea or ocean. On average, seawater in the world's oceans has a salinity of about 3.5% (35 g/L, 35 ppt, 600 mM). This means that every kilogram (roughly one liter by volume) of seawater has appro ...
, and wet ground. This makes the use of radar altimeter
A radar altimeter (RA), also called a radio altimeter (RALT), electronic altimeter, reflection altimeter, or low-range radio altimeter (LRRA), measures altitude above the terrain presently beneath an aircraft or spacecraft by timing how long it t ...
s possible in certain cases. The radar signals that are reflected back towards the radar receiver are the desirable ones that make radar detection work. If the object is ''moving'' either toward or away from the transmitter, there will be a slight change in the frequency
Frequency is the number of occurrences of a repeating event per unit of time. It is also occasionally referred to as ''temporal frequency'' for clarity, and is distinct from ''angular frequency''. Frequency is measured in hertz (Hz) which is eq ...
of the radio waves due to the Doppler effect
The Doppler effect or Doppler shift (or simply Doppler, when in context) is the change in frequency of a wave in relation to an observer who is moving relative to the wave source. It is named after the Austrian physicist Christian Doppler, who ...
.
Radar receivers are usually, but not always, in the same location as the transmitter. The reflected radar signals captured by the receiving antenna are usually very weak. They can be strengthened by electronic amplifiers. More sophisticated methods of signal processing
Signal processing is an electrical engineering subfield that focuses on analyzing, modifying and synthesizing '' signals'', such as sound, images, and scientific measurements. Signal processing techniques are used to optimize transmissions, ...
are also used in order to recover useful radar signals.
The weak absorption of radio waves by the medium through which they pass is what enables radar sets to detect objects at relatively long ranges—ranges at which other electromagnetic wavelengths, such as visible light
Light or visible light is electromagnetic radiation that can be perceived by the human eye. Visible light is usually defined as having wavelengths in the range of 400–700 nanometres (nm), corresponding to frequencies of 750–420 t ...
, infrared light, and ultraviolet light
Ultraviolet (UV) is a form of electromagnetic radiation with wavelength from 10 nm (with a corresponding frequency around 30 PHz) to 400 nm (750 THz), shorter than that of visible light, but longer than X-rays. UV radiatio ...
, are too strongly attenuated. Weather phenomena, such as fog, clouds, rain, falling snow, and sleet, that block visible light are usually transparent to radio waves. Certain radio frequencies that are absorbed or scattered by water vapour, raindrops, or atmospheric gases (especially oxygen) are avoided when designing radars, except when their detection is intended.
Illumination
Radar relies on its own transmissions rather than light from the Sun or the Moon, or fromelectromagnetic wave
In physics, electromagnetic radiation (EMR) consists of waves of the electromagnetic (EM) field, which propagate through space and carry momentum and electromagnetic radiant energy. It includes radio waves, microwaves, infrared, (visible) ...
s emitted by the target objects themselves, such as infrared radiation (heat). This process of directing artificial radio waves towards objects is called ''illumination'', although radio waves are invisible to the human eye as well as optical cameras.
Reflection
 If
If electromagnetic waves
In physics, electromagnetic radiation (EMR) consists of waves of the electromagnetic (EM) field, which propagate through space and carry momentum and electromagnetic radiant energy. It includes radio waves, microwaves, infrared, (visible) ...
travelling through one material meet another material, having a different dielectric constant
The relative permittivity (in older texts, dielectric constant) is the permittivity of a material expressed as a ratio with the electric permittivity of a vacuum. A dielectric is an insulating material, and the dielectric constant of an insula ...
or diamagnetic constant from the first,
the waves will reflect or scatter from the boundary between the materials. This means that a solid object in air or in a vacuum
A vacuum is a space devoid of matter. The word is derived from the Latin adjective ''vacuus'' for "vacant" or " void". An approximation to such vacuum is a region with a gaseous pressure much less than atmospheric pressure. Physicists often ...
, or a significant change in atomic density between the object and what is surrounding it, will usually scatter radar (radio) waves from its surface. This is particularly true for electrically conductive materials such as metal and carbon fibre, making radar well-suited to the detection of aircraft and ships. Radar absorbing material
In materials science, radiation-absorbent material, usually known as RAM, is a material which has been specially designed and shaped to absorption (electromagnetic radiation), absorb incident RF radiation (also known as non-ionising radiation), ...
, containing resistive and sometimes magnetic
Magnetism is the class of physical attributes that are mediated by a magnetic field, which refers to the capacity to induce attractive and repulsive phenomena in other entities. Electric currents and the magnetic moments of elementary particl ...
substances, is used on military vehicles to reduce radar reflection. This is the radio equivalent of painting something a dark colour so that it cannot be seen by the eye at night.
Radar waves scatter in a variety of ways depending on the size (wavelength) of the radio wave and the shape of the target. If the wavelength is much shorter than the target's size, the wave will bounce off in a way similar to the way light is reflected by a mirror
A mirror or looking glass is an object that reflects an image. Light that bounces off a mirror will show an image of whatever is in front of it, when focused through the lens of the eye or a camera. Mirrors reverse the direction of the im ...
. If the wavelength is much longer than the size of the target, the target may not be visible because of poor reflection. Low-frequency radar technology is dependent on resonances for detection, but not identification, of targets. This is described by Rayleigh scattering, an effect that creates Earth's blue sky and red sunsets. When the two length scales are comparable, there may be resonance
Resonance describes the phenomenon of increased amplitude that occurs when the frequency of an applied periodic force (or a Fourier component of it) is equal or close to a natural frequency of the system on which it acts. When an oscil ...
s. Early radars used very long wavelengths that were larger than the targets and thus received a vague signal, whereas many modern systems use shorter wavelengths (a few centimetres or less) that can image objects as small as a loaf of bread.
Short radio waves reflect from curves and corners in a way similar to glint from a rounded piece of glass. The most reflective targets for short wavelengths have 90° angles between the reflective surfaces. A corner reflector
A corner reflector is a retroreflector consisting of three mutually perpendicular, intersecting flat surfaces, which reflects waves directly towards the source, but translated. The three intersecting surfaces often have square shapes. Radar co ...
consists of three flat surfaces meeting like the inside corner of a cube. The structure will reflect waves entering its opening directly back to the source. They are commonly used as radar reflectors to make otherwise difficult-to-detect objects easier to detect. Corner reflectors on boats, for example, make them more detectable to avoid collision or during a rescue. For similar reasons, objects intended to avoid detection will not have inside corners or surfaces and edges perpendicular to likely detection directions, which leads to "odd" looking stealth aircraft
Stealth aircraft are designed to avoid detection using a variety of technologies that reduce reflection/emission of radar, infrared, visible light, radio frequency (RF) spectrum, and audio, collectively known as stealth technology. The F-117 ...
. These precautions do not totally eliminate reflection because of diffraction
Diffraction is defined as the interference or bending of waves around the corners of an obstacle or through an aperture into the region of geometrical shadow of the obstacle/aperture. The diffracting object or aperture effectively becomes a s ...
, especially at longer wavelengths. Half wavelength long wires or strips of conducting material, such as chaff
Chaff (; ) is the dry, scaly protective casing of the seeds of cereal grains or similar fine, dry, scaly plant material (such as scaly parts of flowers or finely chopped straw). Chaff is indigestible by humans, but livestock can eat it. In agri ...
, are very reflective but do not direct the scattered energy back toward the source. The extent to which an object reflects or scatters radio waves is called its radar cross section.
Radar range equation
The power ''Pr'' returning to the receiving antenna is given by the equation: : where * ''P''t = transmitter power * ''G''t =gain
Gain or GAIN may refer to:
Science and technology
* Gain (electronics), an electronics and signal processing term
* Antenna gain
* Gain (laser), the amplification involved in laser emission
* Gain (projection screens)
* Information gain in de ...
of the transmitting antenna
* ''A''r = effective aperture
In electromagnetics and antenna theory, the aperture of an antenna is defined as "A surface, near or on an antenna, on which it is convenient to make
assumptions regarding the field values for the purpose of computing fields at external points. T ...
(area) of the receiving antenna; this can also be expressed as , where
:* = transmitted wavelength
:* ''G''r = gain of receiving antenna
* ''σ'' = radar cross section, or scattering coefficient, of the target
* ''F'' = pattern propagation factor
* ''R''t = distance from the transmitter to the target
* ''R''r = distance from the target to the receiver.
In the common case where the transmitter and the receiver are at the same location, ''R''t = ''R''r and the term ''R''t² ''R''r² can be replaced by ''R''4, where ''R'' is the range.
This yields:
:
This shows that the received power declines as the fourth power of the range, which means that the received power from distant targets is relatively very small.
Additional filtering and pulse integration modifies the radar equation slightly for pulse-Doppler radar performance, which can be used to increase detection range and reduce transmit power.
The equation above with ''F'' = 1 is a simplification for transmission in a vacuum without interference. The propagation factor accounts for the effects of multipath and shadowing and depends on the details of the environment. In a real-world situation, pathloss effects are also considered.
Doppler effect
moving target indication
Moving target indication (MTI) is a mode of operation of a radar to discriminate a target against the clutter. It describes a variety of techniques used for finding moving objects, like an aircraft, and filter out unmoving ones, like hills or tree ...
can interact with Doppler to produce signal cancellation at certain radial velocities, which degrades performance.
Sea-based radar systems, semi-active radar homing
Semi-active radar homing (SARH) is a common type of missile guidance system, perhaps the most common type for longer-range air-to-air and surface-to-air missile systems. The name refers to the fact that the missile itself is only a passive de ...
, active radar homing
Active radar homing (ARH) is a missile guidance method in which a missile contains a radar transceiver (in contrast to semi-active radar homing, which uses only a receiver) and the electronics necessary for it to find and track its target ...
, weather radar
Weather radar, also called weather surveillance radar (WSR) and Doppler weather radar, is a type of radar used to locate precipitation, calculate its motion, and estimate its type (rain, snow, hail etc.). Modern weather radars are mostly pulse- ...
, military aircraft, and radar astronomy
Radar astronomy is a technique of observing nearby astronomical objects by reflecting radio waves or microwaves off target objects and analyzing their reflections. Radar astronomy differs from '' radio astronomy'' in that the latter is a passive o ...
rely on the Doppler effect to enhance performance. This produces information about target velocity during the detection process. This also allows small objects to be detected in an environment containing much larger nearby slow moving objects.
Doppler shift depends upon whether the radar configuration is active or passive. Active radar transmits a signal that is reflected back to the receiver. Passive radar depends upon the object sending a signal to the receiver.
The Doppler frequency shift for active radar is as follows, where is Doppler frequency, is transmit frequency, is radial velocity, and is the speed of light:
:.
Passive radar is applicable to electronic countermeasures
An electronic countermeasure (ECM) is an electrical or electronic device designed to trick or deceive radar, sonar, or other detection systems, like infrared (IR) or lasers. It may be used both offensively and defensively to deny targeting info ...
and radio astronomy
Radio astronomy is a subfield of astronomy that studies celestial objects at radio frequencies. The first detection of radio waves from an astronomical object was in 1933, when Karl Jansky at Bell Telephone Laboratories reported radiation comin ...
as follows:
:.
Only the radial component of the velocity is relevant. When the reflector is moving at right angle to the radar beam, it has no relative velocity. Vehicles and weather moving parallel to the radar beam produce the maximum Doppler frequency shift.
When the transmit frequency () is pulsed, using a pulse repeat frequency of , the resulting frequency spectrum will contain harmonic frequencies above and below with a distance of . As a result, the Doppler measurement is only non-ambiguous if the Doppler frequency shift is less than half of , called the Nyquist frequency
In signal processing, the Nyquist frequency (or folding frequency), named after Harry Nyquist, is a characteristic of a sampler, which converts a continuous function or signal into a discrete sequence. In units of cycles per second ( Hz), it ...
, since the returned frequency otherwise cannot be distinguished from shifting of a harmonic frequency above or below, thus requiring:
:
Or when substituting with :
:
As an example, a Doppler weather radar with a pulse rate of 2 kHz and transmit frequency of 1 GHz can reliably measure weather speed up to at most , thus cannot reliably determine radial velocity of aircraft moving .
Polarization
In allelectromagnetic radiation
In physics, electromagnetic radiation (EMR) consists of waves of the electromagnetic (EM) field, which propagate through space and carry momentum and electromagnetic radiant energy. It includes radio waves, microwaves, infrared, (visib ...
, the electric field is perpendicular to the direction of propagation, and the electric field direction is the polarization of the wave. For a transmitted radar signal, the polarization can be controlled to yield different effects. Radars use horizontal, vertical, linear, and circular polarization to detect different types of reflections. For example, circular polarization
In electrodynamics, circular polarization of an electromagnetic wave is a polarization state in which, at each point, the electromagnetic field of the wave has a constant magnitude and is rotating at a constant rate in a plane perpendicular to ...
is used to minimize the interference caused by rain. Linear polarization returns usually indicate metal surfaces. Random polarization returns usually indicate a fractal
In mathematics, a fractal is a geometric shape containing detailed structure at arbitrarily small scales, usually having a fractal dimension strictly exceeding the topological dimension. Many fractals appear similar at various scales, as ill ...
surface, such as rocks or soil, and are used by navigation radars.
Limiting factors
Beam path and range
refractive index
In optics, the refractive index (or refraction index) of an optical medium is a dimensionless number that gives the indication of the light bending ability of that medium.
The refractive index determines how much the path of light is bent, ...
of air, which is called the radar horizon
The radar horizon is a critical area of performance for aircraft detection systems that is defined by the distance at which the radar beam rises enough above the Earth's surface to make detection of a target at low level impossible. It is asso ...
. Even when the beam is emitted parallel to the ground, the beam rises above the ground as the curvature of the Earth
Spherical Earth or Earth's curvature refers to the approximation of figure of the Earth as a sphere.
The earliest documented mention of the concept dates from around the 5th century BC, when it appears in the writings of Greek philosophers. I ...
sinks below the horizon. Furthermore, the signal is attenuated by the medium the beam crosses, and the beam disperses.
The maximum range of conventional radar can be limited by a number of factors:
* Line of sight, which depends on the height above the ground. Without a direct line of sight, the path of the beam is blocked.
* The maximum non-ambiguous range, which is determined by the pulse repetition frequency. The maximum non-ambiguous range is the distance the pulse can travel to and return from before the next pulse is emitted.
* Radar sensitivity and the power of the return signal as computed in the radar equation. This component includes factors such as the environmental conditions and the size (or radar cross section) of the target.
Noise
Signal noise is an internal source of random variations in the signal, which is generated by all electronic components. Reflected signals decline rapidly as distance increases, so noise introduces a radar range limitation. The noise floor andsignal-to-noise ratio
Signal-to-noise ratio (SNR or S/N) is a measure used in science and engineering that compares the level of a desired signal to the level of background noise. SNR is defined as the ratio of signal power to the noise power, often expressed in de ...
are two different measures of performance that affect range performance. Reflectors that are too far away produce too little signal to exceed the noise floor and cannot be detected. Detection {{Unreferenced, date=March 2018
In general, detection is the action of accessing information without specific cooperation from with the sender.
In the history of radio communications, the term " detector" was first used for a device that detected ...
requires a signal that exceeds the noise floor by at least the signal-to-noise ratio.
Noise typically appears as random variations superimposed on the desired echo signal received in the radar receiver. The lower the power of the desired signal, the more difficult it is to discern it from the noise. The noise figure is a measure of the noise produced by a receiver compared to an ideal receiver, and this needs to be minimized.
Shot noise
Shot noise or Poisson noise is a type of noise which can be modeled by a Poisson process.
In electronics shot noise originates from the discrete nature of electric charge. Shot noise also occurs in photon counting in optical devices, where sh ...
is produced by electrons in transit across a discontinuity, which occurs in all detectors. Shot noise is the dominant source in most receivers. There will also be flicker noise caused by electron transit through amplification devices, which is reduced using heterodyne
A heterodyne is a signal frequency that is created by combining or mixing two other frequencies using a signal processing technique called ''heterodyning'', which was invented by Canadian inventor-engineer Reginald Fessenden. Heterodyning is u ...
amplification. Another reason for heterodyne processing is that for fixed fractional bandwidth, the instantaneous bandwidth increases linearly in frequency. This allows improved range resolution. The one notable exception to heterodyne (downconversion) radar systems is ultra-wideband radar. Here a single cycle, or transient wave, is used similar to UWB communications, see List of UWB channels.
Noise is also generated by external sources, most importantly the natural thermal radiation of the background surrounding the target of interest. In modern radar systems, the internal noise is typically about equal to or lower than the external noise. An exception is if the radar is aimed upwards at clear sky, where the scene is so "cold" that it generates very little thermal noise. The thermal noise is given by ''k''B ''T'' ''B'', where ''T'' is temperature, ''B'' is bandwidth (post matched filter) and ''k''B is the Boltzmann constant
The Boltzmann constant ( or ) is the proportionality factor that relates the average relative kinetic energy of particles in a gas with the thermodynamic temperature of the gas. It occurs in the definitions of the kelvin and the gas constan ...
. There is an appealing intuitive interpretation of this relationship in a radar. Matched filtering allows the entire energy received from a target to be compressed into a single bin (be it a range, Doppler, elevation, or azimuth bin). On the surface it appears that then within a fixed interval of time, perfect, error free, detection could be obtained. This is done by compressing all energy into an infinitesimal time slice. What limits this approach in the real world is that, while time is arbitrarily divisible, current is not. The quantum of electrical energy is an electron, and so the best that can be done is to match filter all energy into a single electron. Since the electron is moving at a certain temperature (Planck spectrum
A black body or blackbody is an idealized physical body that absorbs all incident electromagnetic radiation, regardless of frequency or angle of incidence. The name "black body" is given because it absorbs all colors of light. A black body ...
) this noise source cannot be further eroded. Ultimately, radar, like all macro-scale entities, is profoundly impacted by quantum theory.
Noise is random and target signals are not. Signal processing can take advantage of this phenomenon to reduce the noise floor using two strategies. The kind of signal integration used with moving target indication
Moving target indication (MTI) is a mode of operation of a radar to discriminate a target against the clutter. It describes a variety of techniques used for finding moving objects, like an aircraft, and filter out unmoving ones, like hills or tree ...
can improve noise up to for each stage. The signal can also be split among multiple filters for pulse-Doppler signal processing, which reduces the noise floor by the number of filters. These improvements depend upon coherence
Coherence, coherency, or coherent may refer to the following:
Physics
* Coherence (physics), an ideal property of waves that enables stationary (i.e. temporally and spatially constant) interference
* Coherence (units of measurement), a deriv ...
.
Interference
Radar systems must overcome unwanted signals in order to focus on the targets of interest. These unwanted signals may originate from internal and external sources, both passive and active. The ability of the radar system to overcome these unwanted signals defines itssignal-to-noise ratio
Signal-to-noise ratio (SNR or S/N) is a measure used in science and engineering that compares the level of a desired signal to the level of background noise. SNR is defined as the ratio of signal power to the noise power, often expressed in de ...
(SNR). SNR is defined as the ratio of the signal power to the noise power within the desired signal; it compares the level of a desired target signal to the level of background noise (atmospheric noise and noise generated within the receiver). The higher a system's SNR the better it is at discriminating actual targets from noise signals.
Clutter
Clutter refers to radio frequency (RF) echoes returned from targets which are uninteresting to the radar operators. Such targets include natural objects such as ground, sea, and when not being tasked for meteorological purposes,precipitation
In meteorology, precipitation is any product of the condensation of atmospheric water vapor that falls under gravitational pull from clouds. The main forms of precipitation include drizzle, rain, sleet, snow, ice pellets, graupel and hail. ...
(such as rain, snow or hail), sand storms, animals (especially birds), atmospheric turbulence
In fluid dynamics, turbulence or turbulent flow is fluid motion characterized by chaotic changes in pressure and flow velocity. It is in contrast to a laminar flow, which occurs when a fluid flows in parallel layers, with no disruption between ...
, and other atmospheric effects, such as ionosphere
The ionosphere () is the ionized part of the upper atmosphere of Earth, from about to above sea level, a region that includes the thermosphere and parts of the mesosphere and exosphere. The ionosphere is ionized by solar radiation. It plays ...
reflections, meteor
A meteoroid () is a small rocky or metallic body in outer space.
Meteoroids are defined as objects significantly smaller than asteroids, ranging in size from grains to objects up to a meter wide. Objects smaller than this are classified as mi ...
trails, and hail spike. Clutter may also be returned from man-made objects such as buildings and, intentionally, by radar countermeasures such as chaff
Chaff (; ) is the dry, scaly protective casing of the seeds of cereal grains or similar fine, dry, scaly plant material (such as scaly parts of flowers or finely chopped straw). Chaff is indigestible by humans, but livestock can eat it. In agri ...
.
Some clutter may also be caused by a long radar waveguide
A waveguide is a structure that guides waves, such as electromagnetic waves or sound, with minimal loss of energy by restricting the transmission of energy to one direction. Without the physical constraint of a waveguide, wave intensities de ...
between the radar transceiver and the antenna. In a typical plan position indicator
A plan position indicator (PPI) is a type of radar display that represents the radar antenna in the center of the display, with the distance from it and height above ground drawn as concentric circles. As the radar antenna rotates, a radial trac ...
(PPI) radar with a rotating antenna, this will usually be seen as a "sun" or "sunburst" in the center of the display as the receiver responds to echoes from dust particles and misguided RF in the waveguide. Adjusting the timing between when the transmitter sends a pulse and when the receiver stage is enabled will generally reduce the sunburst without affecting the accuracy of the range, since most sunburst is caused by a diffused transmit pulse reflected before it leaves the antenna. Clutter is considered a passive interference source, since it only appears in response to radar signals sent by the radar.
Clutter is detected and neutralized in several ways. Clutter tends to appear static between radar scans; on subsequent scan echoes, desirable targets will appear to move, and all stationary echoes can be eliminated. Sea clutter can be reduced by using horizontal polarization, while rain is reduced with circular polarization
In electrodynamics, circular polarization of an electromagnetic wave is a polarization state in which, at each point, the electromagnetic field of the wave has a constant magnitude and is rotating at a constant rate in a plane perpendicular to ...
(meteorological radars wish for the opposite effect, and therefore use linear polarization to detect precipitation). Other methods attempt to increase the signal-to-clutter ratio.
Clutter moves with the wind or is stationary. Two common strategies to improve measure or performance in a clutter environment are:
:* Moving target indication, which integrates successive pulses
:* Doppler processing, which uses filters to separate clutter from desirable signals
The most effective clutter reduction technique is pulse-Doppler radar
A pulse-Doppler radar is a radar system that determines the range to a target using pulse-timing techniques, and uses the Doppler effect of the returned signal to determine the target object's velocity. It combines the features of pulse radars and ...
. Doppler separates clutter from aircraft and spacecraft using a frequency spectrum, so individual signals can be separated from multiple reflectors located in the same volume using velocity differences. This requires a coherent transmitter. Another technique uses a moving target indicator
Moving target indication (MTI) is a mode of operation of a radar to discriminate a target against the clutter. It describes a variety of techniques used for finding moving objects, like an aircraft, and filter out unmoving ones, like hills or tre ...
that subtracts the receive signal from two successive pulses using phase to reduce signals from slow moving objects. This can be adapted for systems that lack a coherent transmitter, such as time-domain pulse-amplitude radar.
Constant false alarm rate
Constant false alarm rate (CFAR) detection refers to a common form of adaptive algorithm used in radar systems to detect target returns against a background of noise, clutter and interference.
Principle
In the radar receiver, the returning echo ...
, a form of automatic gain control
Automatic gain control (AGC) is a closed-loop feedback regulating circuit in an amplifier or chain of amplifiers, the purpose of which is to maintain a suitable signal amplitude at its output, despite variation of the signal amplitude at the inpu ...
(AGC), is a method that relies on clutter returns far outnumbering echoes from targets of interest. The receiver's gain is automatically adjusted to maintain a constant level of overall visible clutter. While this does not help detect targets masked by stronger surrounding clutter, it does help to distinguish strong target sources. In the past, radar AGC was electronically controlled and affected the gain of the entire radar receiver. As radars evolved, AGC became computer-software controlled and affected the gain with greater granularity in specific detection cells.
atmospheric ducting
In telecommunications, an atmospheric duct is a horizontal layer in the lower atmosphere in which the vertical refractive index gradients are such that radio signals (and light rays) are guided or ducted, tend to follow the curvature of the E ...
or ionospheric reflection
In radio communication, skywave or skip refers to the propagation of radio waves reflected or refracted back toward Earth from the ionosphere, an electrically charged layer of the upper atmosphere. Since it is not limited by the curvature of ...
/refraction
In physics, refraction is the redirection of a wave as it passes from one medium to another. The redirection can be caused by the wave's change in speed or by a change in the medium. Refraction of light is the most commonly observed phenomen ...
(e.g., anomalous propagation Anomalous propagation (sometimes shortened to anaprop or anoprop) Peter Meischner (ed.), ''Weather Radar: Principles and Advanced Applications'', Springer Science & Business Media, 2005, page 144 includes different forms of radio propagation due to ...
). This clutter type is especially bothersome since it appears to move and behave like other normal (point) targets of interest. In a typical scenario, an aircraft echo is reflected from the ground below, appearing to the receiver as an identical target below the correct one. The radar may try to unify the targets, reporting the target at an incorrect height, or eliminating it on the basis of jitter
In electronics and telecommunications, jitter is the deviation from true periodicity of a presumably periodic signal, often in relation to a reference clock signal. In clock recovery applications it is called timing jitter. Jitter is a signific ...
or a physical impossibility. Terrain bounce jamming exploits this response by amplifying the radar signal and directing it downward. These problems can be overcome by incorporating a ground map of the radar's surroundings and eliminating all echoes which appear to originate below ground or above a certain height. Monopulse can be improved by altering the elevation algorithm used at low elevation. In newer air traffic control radar equipment, algorithms are used to identify the false targets by comparing the current pulse returns to those adjacent, as well as calculating return improbabilities.
Jamming
Radar jamming refers to radio frequency signals originating from sources outside the radar, transmitting in the radar's frequency and thereby masking targets of interest. Jamming may be intentional, as with anelectronic warfare
Electronic warfare (EW) is any action involving the use of the electromagnetic spectrum (EM spectrum) or directed energy to control the spectrum, attack an enemy, or impede enemy assaults. The purpose of electronic warfare is to deny the opponent ...
tactic, or unintentional, as with friendly forces operating equipment that transmits using the same frequency range. Jamming is considered an active interference source, since it is initiated by elements outside the radar and in general unrelated to the radar signals.
Jamming is problematic to radar since the jamming signal only needs to travel one way (from the jammer to the radar receiver) whereas the radar echoes travel two ways (radar-target-radar) and are therefore significantly reduced in power by the time they return to the radar receiver in accordance with inverse-square law
In science, an inverse-square law is any scientific law stating that a specified physical quantity is inversely proportional to the square of the distance from the source of that physical quantity. The fundamental cause for this can be unders ...
. Jammers therefore can be much less powerful than their jammed radars and still effectively mask targets along the line of sight from the jammer to the radar (''mainlobe jamming''). Jammers have an added effect of affecting radars along other lines of sight through the radar receiver's sidelobe
In antenna engineering, sidelobes are the lobes (local maxima) of the far field radiation pattern of an antenna or other radiation source, that are not the '' main lobe''.
The radiation pattern of most antennas shows a pattern of "''lobe ...
s (''sidelobe jamming'').
Mainlobe jamming can generally only be reduced by narrowing the mainlobe solid angle
In geometry, a solid angle (symbol: ) is a measure of the amount of the field of view from some particular point that a given object covers. That is, it is a measure of how large the object appears to an observer looking from that point.
The poi ...
and cannot fully be eliminated when directly facing a jammer which uses the same frequency and polarization as the radar. Sidelobe jamming can be overcome by reducing receiving sidelobes in the radar antenna design and by using an omnidirectional antenna
In radio communication, an omnidirectional antenna is a class of antenna which radiates equal radio power in all directions perpendicular to an axis (azimuthal directions), with power varying with angle to the axis ( elevation angle), declining ...
to detect and disregard non-mainlobe signals. Other anti-jamming techniques are frequency hopping and polarization.
Signal processing
Distance measurement
Transit time
 One way to obtain a distance measurement (ranging) is based on the time-of-flight: transmit a short pulse of radio signal (electromagnetic radiation) and measure the time it takes for the reflection to return. The distance is one-half the round trip time multiplied by the speed of the signal. The factor of one-half comes from the fact that the signal has to travel to the object and back again. Since radio waves travel at the
One way to obtain a distance measurement (ranging) is based on the time-of-flight: transmit a short pulse of radio signal (electromagnetic radiation) and measure the time it takes for the reflection to return. The distance is one-half the round trip time multiplied by the speed of the signal. The factor of one-half comes from the fact that the signal has to travel to the object and back again. Since radio waves travel at the speed of light
The speed of light in vacuum, commonly denoted , is a universal physical constant that is important in many areas of physics. The speed of light is exactly equal to ). According to the special theory of relativity, is the upper limit fo ...
, accurate distance measurement requires high-speed electronics.
In most cases, the receiver does not detect the return while the signal is being transmitted. Through the use of a duplexer, the radar switches between transmitting and receiving at a predetermined rate.
A similar effect imposes a maximum range as well. In order to maximize range, longer times between pulses should be used, referred to as a pulse repetition time, or its reciprocal, pulse repetition frequency.
These two effects tend to be at odds with each other, and it is not easy to combine both good short range and good long range in a single radar. This is because the short pulses needed for a good minimum range broadcast have less total energy, making the returns much smaller and the target harder to detect. This could be offset by using more pulses, but this would shorten the maximum range. So each radar uses a particular type of signal. Long-range radars tend to use long pulses with long delays between them, and short range radars use smaller pulses with less time between them. As electronics have improved many radars now can change their pulse repetition frequency, thereby changing their range. The newest radars fire two pulses during one cell, one for short range (about ) and a separate signal for longer ranges (about ).
Distance may also be measured as a function of time. The radar mile is the time it takes for a radar pulse to travel one nautical mile
A nautical mile is a unit of length used in air, marine, and space navigation, and for the definition of territorial waters. Historically, it was defined as the meridian arc length corresponding to one minute ( of a degree) of latitude. Tod ...
, reflect off a target, and return to the radar antenna. Since a nautical mile is defined as 1,852 m, then dividing this distance by the speed of light (299,792,458 m/s), and then multiplying the result by 2 yields a result of 12.36 μs in duration.
Frequency modulation
radar altimeter
A radar altimeter (RA), also called a radio altimeter (RALT), electronic altimeter, reflection altimeter, or low-range radio altimeter (LRRA), measures altitude above the terrain presently beneath an aircraft or spacecraft by timing how long it t ...
s. In these systems a "carrier" radar signal is frequency modulated in a predictable way, typically varying up and down with a sine wave
A sine wave, sinusoidal wave, or just sinusoid is a mathematical curve defined in terms of the '' sine'' trigonometric function, of which it is the graph. It is a type of continuous wave and also a smooth periodic function. It occurs often in ...
or sawtooth pattern at audio frequencies. The signal is then sent out from one antenna and received on another, typically located on the bottom of the aircraft, and the signal can be continuously compared using a simple ''beat frequency'' modulator that produces an audio frequency tone from the returned signal and a portion of the transmitted signal.
The modulation index The modulation index (or modulation depth) of a modulation
In electronics and telecommunications, modulation is the process of varying one or more properties of a periodic waveform, called the '' carrier signal'', with a separate signal called ...
riding on the receive signal is proportional to the time delay between the radar and the reflector. The frequency shift becomes greater with greater time delay. The frequency shift is directly proportional to the distance travelled. That distance can be displayed on an instrument, and it may also be available via the transponder
In telecommunications, a transponder is a device that, upon receiving a signal, emits a different signal in response. The term is a blend of ''transmitter'' and ''responder''.
In air navigation or radio frequency identification, a flight trans ...
. This signal processing is similar to that used in speed detecting Doppler radar. Example systems using this approach are AZUSA, MISTRAM, and UDOP
The UDOP (UHF Doppler) multistatic radar and multiradar system (MSRS) utilizes Doppler radar for missile tracking and trajectory measurement. A target is illuminated at 450MHz. Five receiving stations, located along the baselines with the lengths ...
.
Terrestrial radar uses low-power FM signals that cover a larger frequency range. The multiple reflections are analyzed mathematically for pattern changes with multiple passes creating a computerized synthetic image. Doppler effects are used which allows slow moving objects to be detected as well as largely eliminating "noise" from the surfaces of bodies of water.
Pulse compression
The two techniques outlined above both have their disadvantages. The pulse timing technique has an inherent tradeoff in that the accuracy of the distance measurement is inversely related to the length of the pulse, while the energy, and thus direction range, is directly related. Increasing power for longer range while maintaining accuracy demands extremely high peak power, with 1960searly warning radar
An early-warning radar is any radar system used primarily for the long-range detection of its targets, i.e., allowing defences to be alerted as ''early'' as possible before the intruder reaches its target, giving the air defences the maximum ...
s often operating in the tens of megawatts. The continuous wave methods spread this energy out in time and thus require much lower peak power compared to pulse techniques, but requires some method of allowing the sent and received signals to operate at the same time, often demanding two separate antennas.
The introduction of new electronics in the 1960s allowed the two techniques to be combined. It starts with a longer pulse that is also frequency modulated. Spreading the broadcast energy out in time means lower peak energies can be used, with modern examples typically on the order of tens of kilowatts. On reception, the signal is sent into a system that delays different frequencies by different times. The resulting output is a much shorter pulse that is suitable for accurate distance measurement, while also compressing the received energy into a much higher energy peak and thus reducing the signal-to-noise ratio. The technique is largely universal on modern large radars.
Speed measurement
Speed
In everyday use and in kinematics, the speed (commonly referred to as ''v'') of an object is the magnitude of the change of its position over time or the magnitude of the change of its position per unit of time; it is thus a scalar quant ...
is the change in distance to an object with respect to time. Thus the existing system for measuring distance, combined with a memory capacity to see where the target last was, is enough to measure speed. At one time the memory consisted of a user making grease pencil marks on the radar screen and then calculating the speed using a slide rule. Modern radar systems perform the equivalent operation faster and more accurately using computers.
If the transmitter's output is coherent (phase synchronized), there is another effect that can be used to make almost instant speed measurements (no memory is required), known as the Doppler effect
The Doppler effect or Doppler shift (or simply Doppler, when in context) is the change in frequency of a wave in relation to an observer who is moving relative to the wave source. It is named after the Austrian physicist Christian Doppler, who ...
. Most modern radar systems use this principle into Doppler radar
A Doppler radar is a specialized radar that uses the Doppler effect to produce velocity data about objects at a distance. It does this by bouncing a microwave signal off a desired target and analyzing how the object's motion has altered the fr ...
and pulse-Doppler radar
A pulse-Doppler radar is a radar system that determines the range to a target using pulse-timing techniques, and uses the Doppler effect of the returned signal to determine the target object's velocity. It combines the features of pulse radars and ...
systems (weather radar
Weather radar, also called weather surveillance radar (WSR) and Doppler weather radar, is a type of radar used to locate precipitation, calculate its motion, and estimate its type (rain, snow, hail etc.). Modern weather radars are mostly pulse- ...
, military radar). The Doppler effect is only able to determine the relative speed of the target along the line of sight from the radar to the target. Any component of target velocity perpendicular to the line of sight cannot be determined by using the Doppler effect alone, but it can be determined by tracking the target's azimuth
An azimuth (; from ar, اَلسُّمُوت, as-sumūt, the directions) is an angular measurement in a spherical coordinate system. More specifically, it is the horizontal angle from a cardinal direction, most commonly north.
Mathematical ...
over time.
It is possible to make a Doppler radar without any pulsing, known as a continuous-wave radar (CW radar), by sending out a very pure signal of a known frequency. CW radar is ideal for determining the radial component of a target's velocity. CW radar is typically used by traffic enforcement to measure vehicle speed quickly and accurately where the range is not important.
When using a pulsed radar, the variation between the phase of successive returns gives the distance the target has moved between pulses, and thus its speed can be calculated.
Other mathematical developments in radar signal processing include time-frequency analysis (Weyl Heisenberg or wavelet
A wavelet is a wave-like oscillation with an amplitude that begins at zero, increases or decreases, and then returns to zero one or more times. Wavelets are termed a "brief oscillation". A taxonomy of wavelets has been established, based on the num ...
), as well as the chirplet transform which makes use of the change of frequency of returns from moving targets ("chirp").
Pulse-Doppler signal processing
 Pulse-Doppler signal processing includes frequency filtering in the detection process. The space between each transmit pulse is divided into range cells or range gates. Each cell is filtered independently much like the process used by a
Pulse-Doppler signal processing includes frequency filtering in the detection process. The space between each transmit pulse is divided into range cells or range gates. Each cell is filtered independently much like the process used by a spectrum analyzer
A spectrum analyzer measures the magnitude of an input signal versus frequency within the full frequency range of the instrument. The primary use is to measure the power of the spectrum of known and unknown signals. The input signal that most co ...
to produce the display showing different frequencies. Each different distance produces a different spectrum. These spectra are used to perform the detection process. This is required to achieve acceptable performance in hostile environments involving weather, terrain, and electronic countermeasures.
The primary purpose is to measure both the amplitude and frequency of the aggregate reflected signal from multiple distances. This is used with weather radar
Weather radar, also called weather surveillance radar (WSR) and Doppler weather radar, is a type of radar used to locate precipitation, calculate its motion, and estimate its type (rain, snow, hail etc.). Modern weather radars are mostly pulse- ...
to measure radial wind velocity and precipitation rate in each different volume of air. This is linked with computing systems to produce a real-time electronic weather map. Aircraft safety depends upon continuous access to accurate weather radar information that is used to prevent injuries and accidents. Weather radar uses a low PRF. Coherency requirements are not as strict as those for military systems because individual signals ordinarily do not need to be separated. Less sophisticated filtering is required, and range ambiguity processing is not normally needed with weather radar in comparison with military radar intended to track air vehicles.
The alternate purpose is " look-down/shoot-down" capability required to improve military air combat survivability. Pulse-Doppler is also used for ground based surveillance radar required to defend personnel and vehicles. Pulse-doppler signal processing increases the maximum detection distance using less radiation close to aircraft pilots, shipboard personnel, infantry, and artillery. Reflections from terrain, water, and weather produce signals much larger than aircraft and missiles, which allows fast moving vehicles to hide using nap-of-the-earth
Nap-of-the-earth (NOE) is a type of very low-altitude flight course used by military aircraft to avoid enemy detection and attack in a high-threat environment. Other, mostly older terms include "ground-hugging", "terrain masking", "flying under t ...
flying techniques and stealth technology
Stealth technology, also termed low observable technology (LO technology), is a sub-discipline of military tactics and passive and active electronic countermeasures, which covers a range of methods used to make personnel, aircraft, ships, su ...
to avoid detection until an attack vehicle is too close to destroy. Pulse-Doppler signal processing incorporates more sophisticated electronic filtering that safely eliminates this kind of weakness. This requires the use of medium pulse-repetition frequency with phase coherent hardware that has a large dynamic range. Military applications require medium PRF which prevents range from being determined directly, and range ambiguity resolution processing is required to identify the true range of all reflected signals. Radial movement is usually linked with Doppler frequency to produce a lock signal that cannot be produced by radar jamming signals. Pulse-Doppler signal processing also produces audible signals that can be used for threat identification.
Reduction of interference effects
Signal processing
Signal processing is an electrical engineering subfield that focuses on analyzing, modifying and synthesizing '' signals'', such as sound, images, and scientific measurements. Signal processing techniques are used to optimize transmissions, ...
is employed in radar systems to reduce the radar interference effects. Signal processing techniques include moving target indication
Moving target indication (MTI) is a mode of operation of a radar to discriminate a target against the clutter. It describes a variety of techniques used for finding moving objects, like an aircraft, and filter out unmoving ones, like hills or tree ...
, Pulse-Doppler signal processing, moving target detection processors, correlation with secondary surveillance radar targets, space-time adaptive processing, and track-before-detect In radar technology and similar fields, track-before-detect (TBD) is a concept according to which a signal is tracked before declaring it a target. In this approach, the sensor data about a tentative target are integrated over time and may yield d ...
. Constant false alarm rate
Constant false alarm rate (CFAR) detection refers to a common form of adaptive algorithm used in radar systems to detect target returns against a background of noise, clutter and interference.
Principle
In the radar receiver, the returning echo ...
and digital terrain model
A digital elevation model (DEM) or digital surface model (DSM) is a 3D computer graphics representation of elevation data to represent terrain or overlaying objects, commonly of a planet, moon, or asteroid. A "global DEM" refers to a discret ...
processing are also used in clutter environments.
Plot and track extraction
A Track algorithm is a radar performance enhancement strategy. Tracking algorithms provide the ability to predict future position of multiple moving objects based on the history of the individual positions being reported by sensor systems. Historical information is accumulated and used to predict future position for use with air traffic control, threat estimation, combat system doctrine, gun aiming, and missile guidance. Position data is accumulated by radar sensors over the span of a few minutes. There are four common track algorithms. * Nearest neighbour algorithm * Probabilistic Data Association * Multiple Hypothesis Tracking * Interactive Multiple Model (IMM) Radar video returns from aircraft can be subjected to a plot extraction process whereby spurious and interfering signals are discarded. A sequence of target returns can be monitored through a device known as a plot extractor. The non-relevant real time returns can be removed from the displayed information and a single plot displayed. In some radar systems, or alternatively in the command and control system to which the radar is connected, a radar tracker is used to associate the sequence of plots belonging to individual targets and estimate the targets' headings and speeds.Engineering
transmitter
In electronics and telecommunications, a radio transmitter or just transmitter is an electronic device which produces radio waves with an antenna. The transmitter itself generates a radio frequency alternating current, which is applied to the ...
that generates the radio signal with an oscillator such as a klystron or a magnetron and controls its duration by a modulator.
* A waveguide
A waveguide is a structure that guides waves, such as electromagnetic waves or sound, with minimal loss of energy by restricting the transmission of energy to one direction. Without the physical constraint of a waveguide, wave intensities de ...
that links the transmitter and the antenna.
* A duplexer
A duplexer is an electronic device that allows bi-directional ( duplex) communication over a single path. In radar and radio communications systems, it isolates the receiver from the transmitter while permitting them to share a common antenna. ...
that serves as a switch between the antenna and the transmitter or the receiver for the signal when the antenna is used in both situations.
* A receiver. Knowing the shape of the desired received signal (a pulse), an optimal receiver can be designed using a matched filter
In signal processing, a matched filter is obtained by correlating a known delayed signal, or ''template'', with an unknown signal to detect the presence of the template in the unknown signal. This is equivalent to convolving the unknown signal w ...
.
* A display processor to produce signals for human readable output devices.
* An electronic section that controls all those devices and the antenna to perform the radar scan ordered by software.
* A link to end user devices and displays.
Antenna design
 Radio signals broadcast from a single antenna will spread out in all directions, and likewise a single antenna will receive signals equally from all directions. This leaves the radar with the problem of deciding where the target object is located.
Early systems tended to use omnidirectional broadcast antennas, with directional receiver antennas which were pointed in various directions. For instance, the first system to be deployed, Chain Home, used two straight antennas at
Radio signals broadcast from a single antenna will spread out in all directions, and likewise a single antenna will receive signals equally from all directions. This leaves the radar with the problem of deciding where the target object is located.
Early systems tended to use omnidirectional broadcast antennas, with directional receiver antennas which were pointed in various directions. For instance, the first system to be deployed, Chain Home, used two straight antennas at right angle
In geometry and trigonometry, a right angle is an angle of exactly 90 degrees or radians corresponding to a quarter turn. If a ray is placed so that its endpoint is on a line and the adjacent angles are equal, then they are right angles. Th ...
s for reception, each on a different display. The maximum return would be detected with an antenna at right angles to the target, and a minimum with the antenna pointed directly at it (end on). The operator could determine the direction to a target by rotating the antenna so one display showed a maximum while the other showed a minimum.
One serious limitation with this type of solution is that the broadcast is sent out in all directions, so the amount of energy in the direction being examined is a small part of that transmitted. To get a reasonable amount of power on the "target", the transmitting aerial should also be directional.
Parabolic reflector
 More modern systems use a steerable parabolic "dish" to create a tight broadcast beam, typically using the same dish as the receiver. Such systems often combine two radar frequencies in the same antenna in order to allow automatic steering, or ''radar lock''.
Parabolic reflectors can be either symmetric parabolas or spoiled parabolas:
Symmetric parabolic antennas produce a narrow "pencil" beam in both the X and Y dimensions and consequently have a higher gain. The NEXRAD Pulse-Doppler weather radar uses a symmetric antenna to perform detailed volumetric scans of the atmosphere. Spoiled parabolic antennas produce a narrow beam in one dimension and a relatively wide beam in the other. This feature is useful if target detection over a wide range of angles is more important than target location in three dimensions. Most 2D surveillance radars use a spoiled parabolic antenna with a narrow azimuthal beamwidth and wide vertical beamwidth. This beam configuration allows the radar operator to detect an aircraft at a specific azimuth but at an indeterminate height. Conversely, so-called "nodder" height finding radars use a dish with a narrow vertical beamwidth and wide azimuthal beamwidth to detect an aircraft at a specific height but with low azimuthal precision.
More modern systems use a steerable parabolic "dish" to create a tight broadcast beam, typically using the same dish as the receiver. Such systems often combine two radar frequencies in the same antenna in order to allow automatic steering, or ''radar lock''.
Parabolic reflectors can be either symmetric parabolas or spoiled parabolas:
Symmetric parabolic antennas produce a narrow "pencil" beam in both the X and Y dimensions and consequently have a higher gain. The NEXRAD Pulse-Doppler weather radar uses a symmetric antenna to perform detailed volumetric scans of the atmosphere. Spoiled parabolic antennas produce a narrow beam in one dimension and a relatively wide beam in the other. This feature is useful if target detection over a wide range of angles is more important than target location in three dimensions. Most 2D surveillance radars use a spoiled parabolic antenna with a narrow azimuthal beamwidth and wide vertical beamwidth. This beam configuration allows the radar operator to detect an aircraft at a specific azimuth but at an indeterminate height. Conversely, so-called "nodder" height finding radars use a dish with a narrow vertical beamwidth and wide azimuthal beamwidth to detect an aircraft at a specific height but with low azimuthal precision.
Types of scan
* Primary Scan: A scanning technique where the main antenna aerial is moved to produce a scanning beam, examples include circular scan, sector scan, etc. * Secondary Scan: A scanning technique where the antenna feed is moved to produce a scanning beam, examples include conical scan, unidirectional sector scan, lobe switching, etc. * Palmer Scan: A scanning technique that produces a scanning beam by moving the main antenna and its feed. A Palmer Scan is a combination of a Primary Scan and a Secondary Scan. *Conical scanning
Conical scanning is a system used in early radar units to improve their accuracy, as well as making it easier to steer the antenna properly to point at a target. Conical scanning is similar in concept to the earlier lobe switching concept used ...
: The radar beam is rotated in a small circle around the "boresight" axis, which is pointed at the target.
Slotted waveguide
 Applied similarly to the parabolic reflector, the slotted waveguide is moved mechanically to scan and is particularly suitable for non-tracking surface scan systems, where the vertical pattern may remain constant. Owing to its lower cost and less wind exposure, shipboard, airport surface, and harbour surveillance radars now use this approach in preference to a parabolic antenna.
Applied similarly to the parabolic reflector, the slotted waveguide is moved mechanically to scan and is particularly suitable for non-tracking surface scan systems, where the vertical pattern may remain constant. Owing to its lower cost and less wind exposure, shipboard, airport surface, and harbour surveillance radars now use this approach in preference to a parabolic antenna.
Phased array
 Another method of steering is used in a
Another method of steering is used in a phased array
In antenna theory, a phased array usually means an electronically scanned array, a computer-controlled array of antennas which creates a beam of radio waves that can be electronically steered to point in different directions without moving th ...
radar.
Phased array antennas are composed of evenly spaced similar antenna elements, such as aerials or rows of slotted waveguide. Each antenna element or group of antenna elements incorporates a discrete phase shift that produces a phase gradient across the array. For example, array elements producing a 5 degree phase shift for each wavelength across the array face will produce a beam pointed 5 degrees away from the centerline perpendicular to the array face. Signals travelling along that beam will be reinforced. Signals offset from that beam will be cancelled. The amount of reinforcement is antenna gain
In electromagnetics, an antenna's gain is a key performance parameter which combines the antenna's directivity and radiation efficiency. The term ''power gain'' has been deprecated by IEEE. In a transmitting antenna, the gain describes ho ...
. The amount of cancellation is side-lobe suppression.
Phased array radars have been in use since the earliest years of radar in World War II (Mammut radar
The FuMG 41/42 Mammut was a long-range, phased array, early warning radar built by Germany in the latter days of World War II. Developed by the GEMA company, it consisted of six or eight ''Freya'' antenna arrays, switched together and coupled to ...
), but electronic device limitations led to poor performance. Phased array radars were originally used for missile defence (see for example Safeguard Program
The Safeguard Program was a U.S. Army anti-ballistic missile (ABM) system designed to protect the U.S. Air Force's Minuteman ICBM silos from attack, thus preserving the US's nuclear deterrent fleet. It was intended primarily to protect against ...
). They are the heart of the ship-borne Aegis Combat System
The Aegis Combat System is an American integrated naval weapons system developed by the Missile and Surface Radar Division of RCA, and it is now produced by Lockheed Martin.
Initially used by the United States Navy, Aegis is now used also by ...
and the Patriot Missile System. The massive redundancy associated with having a large number of array elements increases reliability at the expense of gradual performance degradation that occurs as individual phase elements fail. To a lesser extent, Phased array radars have been used in weather
Weather is the state of the atmosphere, describing for example the degree to which it is hot or cold, wet or dry, calm or stormy, clear or cloudy. On Earth, most weather phenomena occur in the lowest layer of the planet's atmosphere, the ...
surveillance
Surveillance is the monitoring of behavior, many activities, or information for the purpose of information gathering, influencing, managing or directing. This can include observation from a distance by means of electronic equipment, such as ...
. As of 2017, NOAA plans to implement a national network of Multi-Function Phased array radars throughout the United States within 10 years, for meteorological studies and flight monitoring.
Phased array antennas can be built to conform to specific shapes, like missiles, infantry support vehicles, ships, and aircraft.
As the price of electronics has fallen, phased array radars have become more common. Almost all modern military radar systems are based on phased arrays, where the small additional cost is offset by the improved reliability of a system with no moving parts. Traditional moving-antenna designs are still widely used in roles where cost is a significant factor such as air traffic surveillance and similar systems.
Phased array radars are valued for use in aircraft since they can track multiple targets. The first aircraft to use a phased array radar was the B-1B Lancer
The Rockwell B-1 Lancer is a supersonic variable-sweep wing, heavy bomber used by the United States Air Force. It is commonly called the "Bone" (from "B-One"). It is one of three strategic bombers serving in the U.S. Air Force fleet along with ...
. The first fighter aircraft to use phased array radar was the Mikoyan MiG-31. The MiG-31M's SBI-16 Zaslon Passive electronically scanned array radar was considered to be the world's most powerful fighter radar, until the AN/APG-77
The AN/APG-77 is a multifunction low probability of intercept radar installed on the F-22 Raptor fighter aircraft. The radar was designed and initially built by Westinghouse and Texas Instruments, and production continued with their respective s ...
Active electronically scanned array
An active electronically scanned array (AESA) is a type of phased array antenna, which is a computer-controlled array antenna in which the beam of radio waves can be electronically steered to point in different directions without moving the an ...
was introduced on the Lockheed Martin F-22 Raptor
The Lockheed Martin F-22 Raptor is an American single-seat, twin-engine, all-weather stealth tactical fighter aircraft developed for the United States Air Force (USAF). As the result of the USAF's Advanced Tactical Fighter (ATF) program, th ...
.
Phased-array interferometry
Interferometry is a technique which uses the '' interference'' of superimposed waves to extract information. Interferometry typically uses electromagnetic waves and is an important investigative technique in the fields of astronomy, fiber o ...
or aperture synthesis
Aperture synthesis or synthesis imaging is a type of interferometry that mixes signals from a collection of telescopes to produce images having the same angular resolution as an instrument the size of the entire collection. At each separation and ...
techniques, using an array of separate dishes that are phased into a single effective aperture, are not typical for radar applications, although they are widely used in radio astronomy
Radio astronomy is a subfield of astronomy that studies celestial objects at radio frequencies. The first detection of radio waves from an astronomical object was in 1933, when Karl Jansky at Bell Telephone Laboratories reported radiation comin ...
. Because of the thinned array curse, such multiple aperture arrays, when used in transmitters, result in narrow beams at the expense of reducing the total power transmitted to the target. In principle, such techniques could increase spatial resolution, but the lower power means that this is generally not effective.
Aperture synthesis
Aperture synthesis or synthesis imaging is a type of interferometry that mixes signals from a collection of telescopes to produce images having the same angular resolution as an instrument the size of the entire collection. At each separation and ...
by post-processing motion data from a single moving source, on the other hand, is widely used in space and airborne radar system
Airborne or Airborn may refer to:
Arts, entertainment, and media
Films
* ''Airborne'' (1962 film), a 1962 American film directed by James Landis
* ''Airborne'' (1993 film), a comedy–drama film
* ''Airborne'' (1998 film), an action film sta ...
s.
Frequency bands
Antennas generally have to be sized similar to the wavelength of the operational frequency, normally within anorder of magnitude
An order of magnitude is an approximation of the logarithm of a value relative to some contextually understood reference value, usually 10, interpreted as the base of the logarithm and the representative of values of magnitude one. Logarithmic di ...
. This provides a strong incentive to use shorter wavelengths as this will result in smaller antennas. Shorter wavelengths also result in higher resolution due to diffraction, meaning the shaped reflector seen on most radars can also be made smaller for any desired beamwidth.
Opposing the move to smaller wavelengths are a number of practical issues. For one, the electronics needed to produce high power very short wavelengths were generally more complex and expensive than the electronics needed for longer wavelengths or didn't exist at all. Another issue is that the radar equation
Radar is a detection system that uses radio waves to determine the distance (''ranging''), angle, and radial velocity of objects relative to the site. It can be used to detect aircraft, ships, spacecraft, guided missiles, motor vehicles, w ...
's effective aperture figure means that for any given antenna (or reflector) size will be more efficient at longer wavelengths. Additionally, shorter wavelengths may interact with molecules or raindrops in the air, scattering the signal. Very long wavelengths also have additional diffraction effects that make them suitable for over the horizon radars. For this reason, a wide variety of wavelengths are used in different roles.
The traditional band names originated as code-names during World War II and are still in military and aviation use throughout the world. They have been adopted in the United States by the Institute of Electrical and Electronics Engineers
The Institute of Electrical and Electronics Engineers (IEEE) is a 501(c)(3) professional association for electronic engineering and electrical engineering (and associated disciplines) with its corporate office in New York City and its operation ...
and internationally by the International Telecommunication Union
The International Telecommunication Union is a specialized agency of the United Nations responsible for many matters related to information and communication technologies. It was established on 17 May 1865 as the International Telegraph Unio ...
. Most countries have additional regulations to control which parts of each band are available for civilian or military use.
Other users of the radio spectrum, such as the broadcasting
Broadcasting is the distribution of audio or video content to a dispersed audience via any electronic mass communications medium, but typically one using the electromagnetic spectrum (radio waves), in a one-to-many model. Broadcasting began wi ...
and electronic countermeasures
An electronic countermeasure (ECM) is an electrical or electronic device designed to trick or deceive radar, sonar, or other detection systems, like infrared (IR) or lasers. It may be used both offensively and defensively to deny targeting info ...
industries, have replaced the traditional military designations with their own systems.
Modulators
Modulators act to provide the waveform of the RF-pulse. There are two different radar modulator designs: * High voltage switch for non-coherent keyed power-oscillators These modulators consist of a high voltage pulse generator formed from a high voltage supply, a pulse forming network, and a high voltage switch such as a thyratron. They generate short pulses of power to feed, e.g., the magnetron, a special type of vacuum tube that converts DC (usually pulsed) into microwaves. This technology is known as pulsed power. In this way, the transmitted pulse of RF radiation is kept to a defined and usually very short duration. * Hybrid mixers, fed by a waveform generator and an exciter for a complex butcoherent
Coherence, coherency, or coherent may refer to the following:
Physics
* Coherence (physics), an ideal property of waves that enables stationary (i.e. temporally and spatially constant) interference
* Coherence (units of measurement), a deriv ...
waveform. This waveform can be generated by low power/low-voltage input signals. In this case the radar transmitter must be a power-amplifier, e.g., a klystron or a solid state transmitter. In this way, the transmitted pulse is intrapulse-modulated and the radar receiver must use pulse compression techniques.
Coolant
Coherent microwave amplifiers operating above 1,000 watts microwave output, like travelling wave tubes and klystrons, require liquid coolant. The electron beam must contain 5 to 10 times more power than the microwave output, which can produce enough heat to generate plasma. This plasma flows from the collector toward the cathode. The same magnetic focusing that guides the electron beam forces the plasma into the path of the electron beam but flowing in the opposite direction. This introduces FM modulation which degrades Doppler performance. To prevent this, liquid coolant with minimum pressure and flow rate is required, and deionized water is normally used in most high power surface radar systems that use Doppler processing.Coolanol
Coolanol is a trade name for a series of silicate ester industrial coolants. It is manufactured by Exxon Mobil Corporation.
The product meets many MIL-SPEC
A United States defense standard, often called a military standard, "MIL-STD", "MIL-SPE ...
(silicate
In chemistry, a silicate is any member of a family of polyatomic anions consisting of silicon and oxygen, usually with the general formula , where . The family includes orthosilicate (), metasilicate (), and pyrosilicate (, ). The name is a ...
ester
In chemistry, an ester is a compound derived from an oxoacid (organic or inorganic) in which at least one hydroxyl group () is replaced by an alkoxy group (), as in the substitution reaction of a carboxylic acid and an alcohol. Glycerides ...
) was used in several military radars in the 1970s. However, it is hygroscopic
Hygroscopy is the phenomenon of attracting and holding water molecules via either absorption or adsorption from the surrounding environment, which is usually at normal or room temperature. If water molecules become suspended among the substance' ...
, leading to hydrolysis
Hydrolysis (; ) is any chemical reaction in which a molecule of water breaks one or more chemical bonds. The term is used broadly for substitution, elimination, and solvation reactions in which water is the nucleophile.
Biological hydrolysi ...
and formation of highly flammable alcohol. The loss of a U.S. Navy aircraft in 1978 was attributed to a silicate ester fire. Coolanol is also expensive and toxic. The U.S. Navy has instituted a program named Pollution Prevention (P2) to eliminate or reduce the volume and toxicity of waste, air emissions, and effluent discharges. Because of this, Coolanol is used less often today.
Regulations
''Radar'' (also: ''RADAR'') is defined by ''article 1.100'' of the International Telecommunication Union's (ITU)ITU Radio Regulations
The ITU Radio Regulations (short: RR) is a basic document of the International Telecommunication Union (ITU) that regulates on law of nations scale radiocommunication services and the utilisation of radio frequencies. It is the supplementatio ...
(RR) as:ITU Radio Regulations, Section IV. Radio Stations and Systems – Article 1.100, definition: ''radar / RADAR''
Configurations
Radar come in a variety of configurations in the emitter, the receiver, the antenna, wavelength, scan strategies, etc. * Bistatic radar * Continuous-wave radar *Doppler radar
A Doppler radar is a specialized radar that uses the Doppler effect to produce velocity data about objects at a distance. It does this by bouncing a microwave signal off a desired target and analyzing how the object's motion has altered the fr ...
* Fm-cw radar
Continuous-wave radar (CW radar) is a type of radar system where a known stable frequency continuous wave radio energy is transmitted and then received from any reflecting objects. Individual objects can be detected using the Doppler effect, which ...
* Monopulse radar
Monopulse radar is a radar system that uses additional encoding of the radio signal to provide accurate directional information. The name refers to its ability to extract range and direction from a single signal pulse.
Monopulse radar avoids prob ...
* Passive radar
* Planar array radar
The planar array radar is a type of radar that uses a high-gain planar array antenna.
Operation
A fixed delay is established between horizontal arrays in the elevation plane. As the frequency is changed, the phase front across the aperture ten ...
* Pulse-doppler
* Synthetic-aperture radar
Synthetic-aperture radar (SAR) is a form of radar that is used to create two-dimensional images or three-dimensional reconstructions of objects, such as landscapes. SAR uses the motion of the radar antenna over a target region to provide fin ...
** Synthetically thinned aperture radar
* Over-the-horizon radar with Chirp transmitter
An ionosonde, or chirpsounder, is a special radar for the examination of the ionosphere. The basic ionosonde technology was invented in 1925 by Gregory Breit and Merle A. Tuve and further developed in the late 1920s by a number of prominent p ...
See also
*Terrain-following radar
Terrain-following radar (TFR) is a military aerospace technology that allows a very-low-flying aircraft to automatically maintain a relatively constant altitude above ground level and therefore make detection by enemy radar more difficult. It is ...
* Radar imaging
* Radar navigation
* Inverse-square law
In science, an inverse-square law is any scientific law stating that a specified physical quantity is inversely proportional to the square of the distance from the source of that physical quantity. The fundamental cause for this can be unders ...
* Wave radar
* Radar signal characteristics
* Pulse doppler radar
* Acronyms and abbreviations in avionics
Below are abbreviations used in aviation, avionics, aerospace and aeronautics.
A
B
C
D
E
F
G
H
I
J
K
L
M
N
N numbers (turbines)
O
P
Q
R
S
T
U
V
V speeds
W
X
Y
Z
See also
* List of avia ...
;Definitions
* Amplitude-comparison monopulse
* Constant false alarm rate
Constant false alarm rate (CFAR) detection refers to a common form of adaptive algorithm used in radar systems to detect target returns against a background of noise, clutter and interference.
Principle
In the radar receiver, the returning echo ...
* Sensitivity time control
;Application
* Proximity fuze
A proximity fuze (or fuse) is a fuze that detonates an explosive device automatically when the distance to the target becomes smaller than a predetermined value. Proximity fuzes are designed for targets such as planes, missiles, ships at sea, an ...
;Hardware
* Cavity magnetron
* Crossed-field amplifier
A crossed-field amplifier (CFA) is a specialized vacuum tube, first introduced in the mid-1950s and frequently used as a microwave amplifier in very-high-power transmitters.
Raytheon engineer William C. Brown's work to adapt magnetron principle ...
* Gallium arsenide
Gallium arsenide (GaAs) is a III-V direct band gap semiconductor with a zinc blende crystal structure.
Gallium arsenide is used in the manufacture of devices such as microwave frequency integrated circuits, monolithic microwave integrated c ...
* Klystron
* Omniview technology
Omniview technology (also known as surround view or bird view) is a vehicle parking assistant technology that first was introduced in 2007 as the "Around View Monitor" option for the Nissan Elgrand and Infiniti EX. It is designed to assist drive ...
* Radar engineering details
* Radar tower
A radar tower is a tower whose function is to support a radar facility, usually a local airport surveillance radar, and hence often at or in the vicinity of an airport or a military air base. In addition, radar towers are used for the installatio ...
* Radio
Radio is the technology of signaling and communicating using radio waves. Radio waves are electromagnetic waves of frequency between 30 hertz (Hz) and 300 gigahertz (GHz). They are generated by an electronic device called a tr ...
* Travelling-wave tube
;Similar detection and ranging methods
* Lidar
Lidar (, also LIDAR, or LiDAR; sometimes LADAR) is a method for determining ranges (variable distance) by targeting an object or a surface with a laser and measuring the time for the reflected light to return to the receiver. It can also be ...
* LORAN
LORAN, short for long range navigation, was a hyperbolic radio navigation system developed in the United States during World War II. It was similar to the UK's Gee system but operated at lower frequencies in order to provide an improved range ...
* Sonar
Sonar (sound navigation and ranging or sonic navigation and ranging) is a technique that uses sound propagation (usually underwater, as in submarine navigation) to navigate, measure distances (ranging), communicate with or detect objects on o ...
;Historical radars
* List of radars
A radar is an electronic system used to determine and detect the range of target and maps various types of targets.This is a list of radars.
Argentina
Australia
Brazil
Egypt
Europe
India Military
Airborne
*LCA MMR - 3D advanced, ligh ...
* Chain Home
Chain Home, or CH for short, was the codename for the ring of coastal Early Warning radar stations built by the Royal Air Force (RAF) before and during the Second World War to detect and track aircraft. Initially known as RDF, and given the of ...
and Chain Home Low
* Würzburg radar
* Hohentwiel radar
* H2S radar
H2S was the first airborne, ground scanning radar system. It was developed for the Royal Air Force's Bomber Command during World War II to identify targets on the ground for night and all-weather bombing. This allowed attacks outside the ran ...
* SCR-270 radar
The SCR-270 (Set Complete Radio model 270) was one of the first operational early-warning radars. It was the U.S. Army's primary long-distance radar throughout World War II and was deployed around the world. It is also known as the Pearl Harbor ...
Notes and references
Bibliography
References
* Barrett, Dick, "All you ever wanted to know about British air defence radar
'". The Radar Pages. (History and details of various British radar systems) * Buderi, "
'". Privateline.com. (Anecdotal account of the carriage of the world's first high power cavity magnetron from Britain to the US during WW2.) * Ekco Rada
WW2 Shadow Factory
The secret development of British radar. * ES31
* Hollmann, Martin, "
'"
Radar World
* Penley, Bill, and Jonathan Penley, "
��an Introduction''". 2002. * Pub 1310 ''Radar Navigation and Maneuvering Board Manual'', National Imagery and Mapping Agency, Bethesda, MD 2001 (US govt publication '...intended to be used primarily as a manual of instruction in navigation schools and by naval and merchant marine personnel.') * Wesley Stout, 194
Early development and production by Chrysler Corp. during WWII. * Swords, Seán S., "Technical History of the Beginnings of Radar", '' IEE History of Technology Series'', Vol. 6, London: Peter Peregrinus, 1986
General
* * * * * * Burch, David F., ''Radar For Mariners'', McGraw Hill, 2005, . * * * * * Kaiser, Gerald, Chapter 10 in "A Friendly Guide to Wavelets", Birkhauser, Boston, 1994. * * * * * * * Younghusband, Eileen., ''Not an Ordinary Life. How Changing Times Brought Historical Events into my Life'', Cardiff Centre for Lifelong Learning, Cardiff, 2009., (Pages 36–67 contain the experiences of a WAAF radar plotter in WWII.) * Younghusband, Eileen. ''One Woman's War''. Cardiff. Candy Jar Books. 2011. *Technical reading
* * * * * * * * * *External links
MIT Video Course: Introduction to Radar Systems
A set of 10 video lectures developed at Lincoln Laboratory to develop an understanding of radar systems and technologies.
Glossary of radar terminology
{{Authority control Avionics Aircraft instruments Microwave technology Measuring instruments Navigational equipment Air traffic control Science and technology during World War II Targeting (warfare) Radio stations and systems ITU 1940s neologisms Wireless communication systems