parallel axis theorem on:
[Wikipedia]
[Google]
[Amazon]
The parallel axis theorem, also known as Huygens–Steiner theorem, or just as Steiner's theorem, named after
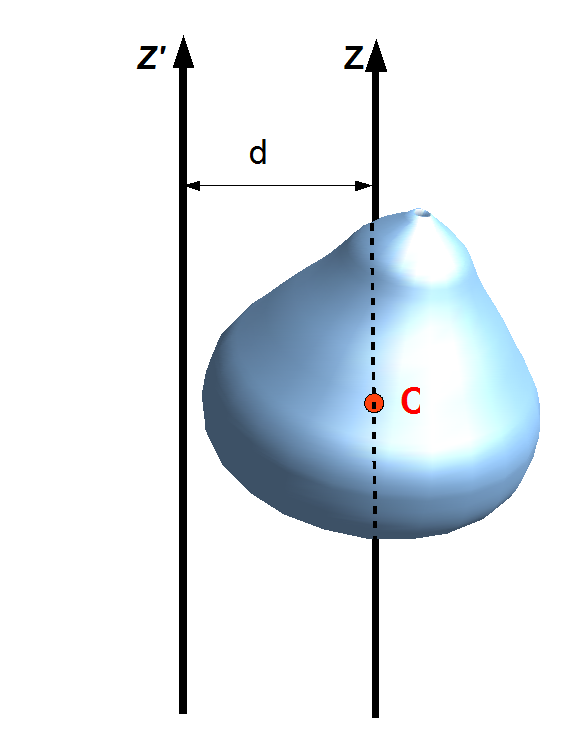 Suppose a body of mass is rotated about an axis passing through the body's
Suppose a body of mass is rotated about an axis passing through the body's
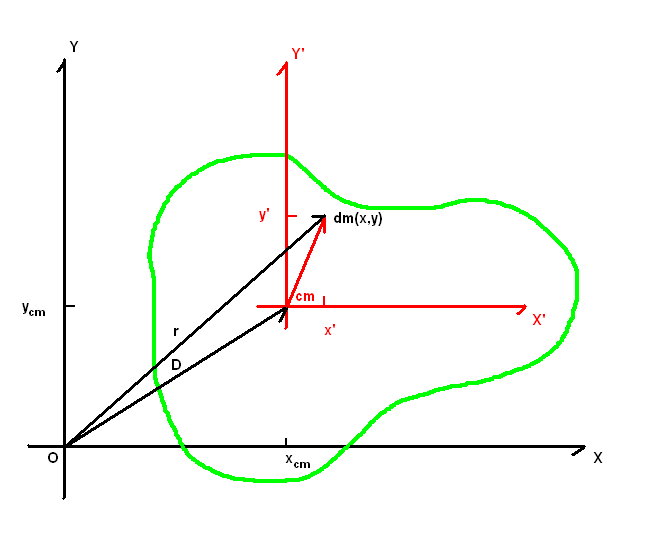 The mass properties of a rigid body that is constrained to move parallel to a plane are defined by its center of mass R = (''x'', ''y'') in this plane, and its polar moment of inertia ''I''''R'' around an axis through R that is perpendicular to the plane. The parallel axis theorem provides a convenient relationship between the moment of inertia IS around an arbitrary point S and the moment of inertia IR about the center of mass R.
Recall that the center of mass R has the property
:
where r is integrated over the volume ''V'' of the body. The polar moment of inertia of a body undergoing planar movement can be computed relative to any reference point S,
:
where S is constant and r is integrated over the volume ''V''.
In order to obtain the moment of inertia ''I''''S'' in terms of the moment of inertia ''I''''R'', introduce the vector d from S to the center of mass R,
:
The first term is the moment of inertia ''I''''R'', the second term is zero by definition of the center of mass, and the last term is the total mass of the body times the square magnitude of the vector d. Thus,
:
which is known as the parallel axis theorem.
The mass properties of a rigid body that is constrained to move parallel to a plane are defined by its center of mass R = (''x'', ''y'') in this plane, and its polar moment of inertia ''I''''R'' around an axis through R that is perpendicular to the plane. The parallel axis theorem provides a convenient relationship between the moment of inertia IS around an arbitrary point S and the moment of inertia IR about the center of mass R.
Recall that the center of mass R has the property
:
where r is integrated over the volume ''V'' of the body. The polar moment of inertia of a body undergoing planar movement can be computed relative to any reference point S,
:
where S is constant and r is integrated over the volume ''V''.
In order to obtain the moment of inertia ''I''''S'' in terms of the moment of inertia ''I''''R'', introduce the vector d from S to the center of mass R,
:
The first term is the moment of inertia ''I''''R'', the second term is zero by definition of the center of mass, and the last term is the total mass of the body times the square magnitude of the vector d. Thus,
:
which is known as the parallel axis theorem.
Dynamics, Theory and Applications
McGraw-Hill, NY, 2005. There is a useful relationship between the inertia matrix relative to the center of mass R and the inertia matrix relative to another point S. This relationship is called the parallel axis theorem. Consider the inertia matrix Sobtained for a rigid system of particles measured relative to a reference point S, given by : where r''i'' defines the position of particle ''P''''i'', ''i'' = 1, ..., ''n''. Recall that 'r''''i'' − ''S''is the skew-symmetric matrix that performs the cross product, : for an arbitrary vector y. Let R be the center of mass of the rigid system, then : where d is the vector from the reference point S to the center of mass R. Use this equation to compute the inertia matrix, : Expand this equation to obtain : The first term is the inertia matrix 'I''''R''relative to the center of mass. The second and third terms are zero by definition of the center of mass R, : And the last term is the total mass of the system multiplied by the square of the skew-symmetric matrix 'd''constructed from d. The result is the parallel axis theorem, : where d is the vector from the reference point S to the center of mass R.
Parallel axis theorem Video about the inertia tensor
Mechanics Physics theorems Christiaan Huygens Moment (physics) fr:Moment d'inertie#Théorème de transport (ou théorème d'Huygens ou théorème de Steiner)
Christiaan Huygens
Christiaan Huygens, Lord of Zeelhem, ( , , ; also spelled Huyghens; la, Hugenius; 14 April 1629 – 8 July 1695) was a Dutch mathematician, physicist, engineer, astronomer, and inventor, who is regarded as one of the greatest scientists o ...
and Jakob Steiner
Jakob Steiner (18 March 1796 – 1 April 1863) was a Swiss mathematician who worked primarily in geometry.
Life
Steiner was born in the village of Utzenstorf, Canton of Bern. At 18, he became a pupil of Heinrich Pestalozzi and afterwards st ...
, can be used to determine the moment of inertia
The moment of inertia, otherwise known as the mass moment of inertia, angular mass, second moment of mass, or most accurately, rotational inertia, of a rigid body is a quantity that determines the torque needed for a desired angular accele ...
or the second moment of area
The second moment of area, or second area moment, or quadratic moment of area and also known as the area moment of inertia, is a geometrical property of an area which reflects how its points are distributed with regard to an arbitrary axis. The ...
of a rigid body
In physics, a rigid body (also known as a rigid object) is a solid body in which deformation is zero or so small it can be neglected. The distance between any two given points on a rigid body remains constant in time regardless of external fo ...
about any axis, given the body's moment of inertia about a parallel
Parallel is a geometric term of location which may refer to:
Computing
* Parallel algorithm
* Parallel computing
* Parallel metaheuristic
* Parallel (software), a UNIX utility for running programs in parallel
* Parallel Sysplex, a cluster o ...
axis through the object's center of gravity
In physics, the center of mass of a distribution of mass in space (sometimes referred to as the balance point) is the unique point where the weighted relative position of the distributed mass sums to zero. This is the point to which a force ma ...
and the perpendicular
In elementary geometry, two geometric objects are perpendicular if they intersect at a right angle (90 degrees or π/2 radians). The condition of perpendicularity may be represented graphically using the '' perpendicular symbol'', ⟂. It c ...
distance
Distance is a numerical or occasionally qualitative measurement of how far apart objects or points are. In physics or everyday usage, distance may refer to a physical length or an estimation based on other criteria (e.g. "two counties over"). ...
between the axes.
Mass moment of inertia
 Suppose a body of mass is rotated about an axis passing through the body's
Suppose a body of mass is rotated about an axis passing through the body's center of mass
In physics, the center of mass of a distribution of mass in space (sometimes referred to as the balance point) is the unique point where the weighted relative position of the distributed mass sums to zero. This is the point to which a force may ...
. The body has a moment of inertia with respect to this axis.
The parallel axis theorem states that if the body is made to rotate instead about a new axis , which is parallel to the first axis and displaced from it by a distance , then the moment of inertia with respect to the new axis is related to by
:
Explicitly, is the perpendicular distance between the axes and .
The parallel axis theorem can be applied with the stretch rule
In classical mechanics, the stretch rule (sometimes referred to as Routh's rule) states that the moment of inertia of a rigid object is unchanged when the object is stretched parallel to an axis of rotation that is a principal axis, provided tha ...
and perpendicular axis theorem The perpendicular axis theorem (or plane figure theorem) states that the moment of inertia of a planar lamina (i.e. 2-D body) about an axis perpendicular to the plane of the lamina is equal to the sum of the moments of inertia of the lamina about t ...
to find moments of inertia for a variety of shapes.
Derivation
We may assume, without loss of generality, that in aCartesian coordinate system
A Cartesian coordinate system (, ) in a plane is a coordinate system that specifies each point uniquely by a pair of numerical coordinates, which are the signed distances to the point from two fixed perpendicular oriented lines, measured in ...
the perpendicular distance between the axes lies along the ''x''-axis and that the center of mass lies at the origin. The moment of inertia relative to the ''z''-axis is
:
The moment of inertia relative to the axis , which is at a distance from the center of mass along the ''x''-axis, is
:
Expanding the brackets yields
:
The first term is and the second term becomes . The integral in the final term is a multiple of the x-coordinate of the center of mass
In physics, the center of mass of a distribution of mass in space (sometimes referred to as the balance point) is the unique point where the weighted relative position of the distributed mass sums to zero. This is the point to which a force may ...
which is zero since the center of mass lies at the origin. So, the equation becomes:
:
Tensor generalization
The parallel axis theorem can be generalized to calculations involving the inertia tensor.A. R. Abdulghany, American Journal of Physics 85, 791 (2017); doi: https://dx.doi.org/10.1119/1.4994835 . Let denote the inertia tensor of a body as calculated at the centre of mass. Then the inertia tensor as calculated relative to a new point is : where is the displacement vector from the centre of mass to the new point, and is theKronecker delta
In mathematics, the Kronecker delta (named after Leopold Kronecker) is a function of two variables, usually just non-negative integers. The function is 1 if the variables are equal, and 0 otherwise:
\delta_ = \begin
0 &\text i \neq j, \\
1 & ...
.
For diagonal elements (when ), displacements perpendicular to the axis of rotation results in the above simplified version of the parallel axis theorem.
The generalized version of the parallel axis theorem can be expressed in the form of coordinate-free notation as
:
where E3 is the identity matrix
In linear algebra, the identity matrix of size n is the n\times n square matrix with ones on the main diagonal and zeros elsewhere.
Terminology and notation
The identity matrix is often denoted by I_n, or simply by I if the size is immaterial or ...
and is the outer product
In linear algebra, the outer product of two coordinate vectors is a matrix. If the two vectors have dimensions ''n'' and ''m'', then their outer product is an ''n'' × ''m'' matrix. More generally, given two tensors (multidimensional arrays of nu ...
.
Further generalization of the parallel axis theorem gives the inertia tensor about any set of orthogonal axes parallel to the reference set of axes x, y and z, associated with the reference inertia tensor, whether or not they pass through the center of mass.A. R. Abdulghany, American Journal of Physics 85, 791 (2017); doi: https://dx.doi.org/10.1119/1.4994835 .
Second moment of area
The parallel axes rule also applies to thesecond moment of area
The second moment of area, or second area moment, or quadratic moment of area and also known as the area moment of inertia, is a geometrical property of an area which reflects how its points are distributed with regard to an arbitrary axis. The ...
(area moment of inertia) for a plane region ''D'':
:
where is the area moment of inertia of ''D'' relative to the parallel axis, is the area moment of inertia of ''D'' relative to its centroid
In mathematics and physics, the centroid, also known as geometric center or center of figure, of a plane figure or solid figure is the arithmetic mean position of all the points in the surface of the figure. The same definition extends to any ...
, is the area of the plane region ''D'', and is the distance from the new axis to the centroid
In mathematics and physics, the centroid, also known as geometric center or center of figure, of a plane figure or solid figure is the arithmetic mean position of all the points in the surface of the figure. The same definition extends to any ...
of the plane region ''D''. The centroid
In mathematics and physics, the centroid, also known as geometric center or center of figure, of a plane figure or solid figure is the arithmetic mean position of all the points in the surface of the figure. The same definition extends to any ...
of ''D'' coincides with the centre of gravity
In physics, the center of mass of a distribution of mass in space (sometimes referred to as the balance point) is the unique point where the weighted relative position of the distributed mass sums to zero. This is the point to which a force may ...
of a physical plate with the same shape that has uniform density.
Polar moment of inertia for planar dynamics
Moment of inertia matrix
The inertia matrix of a rigid system of particles depends on the choice of the reference point.T. R. Kane and D. A. LevinsonDynamics, Theory and Applications
McGraw-Hill, NY, 2005. There is a useful relationship between the inertia matrix relative to the center of mass R and the inertia matrix relative to another point S. This relationship is called the parallel axis theorem. Consider the inertia matrix Sobtained for a rigid system of particles measured relative to a reference point S, given by : where r''i'' defines the position of particle ''P''''i'', ''i'' = 1, ..., ''n''. Recall that 'r''''i'' − ''S''is the skew-symmetric matrix that performs the cross product, : for an arbitrary vector y. Let R be the center of mass of the rigid system, then : where d is the vector from the reference point S to the center of mass R. Use this equation to compute the inertia matrix, : Expand this equation to obtain : The first term is the inertia matrix 'I''''R''relative to the center of mass. The second and third terms are zero by definition of the center of mass R, : And the last term is the total mass of the system multiplied by the square of the skew-symmetric matrix 'd''constructed from d. The result is the parallel axis theorem, : where d is the vector from the reference point S to the center of mass R.
Identities for a skew-symmetric matrix
In order to compare formulations of the parallel axis theorem using skew-symmetric matrices and the tensor formulation, the following identities are useful. Let 'R''be the skew symmetric matrix associated with the position vector R = (''x'', ''y'', ''z''), then the product in the inertia matrix becomes : This product can be computed using the matrix formed by the outer product ''R RTusing the identify : where 'E''3is the 3 × 3 identity matrix. Also notice, that : where tr denotes the sum of the diagonal elements of the outer product matrix, known as its trace.See also
*Christiaan Huygens
Christiaan Huygens, Lord of Zeelhem, ( , , ; also spelled Huyghens; la, Hugenius; 14 April 1629 – 8 July 1695) was a Dutch mathematician, physicist, engineer, astronomer, and inventor, who is regarded as one of the greatest scientists o ...
* Jakob Steiner
Jakob Steiner (18 March 1796 – 1 April 1863) was a Swiss mathematician who worked primarily in geometry.
Life
Steiner was born in the village of Utzenstorf, Canton of Bern. At 18, he became a pupil of Heinrich Pestalozzi and afterwards st ...
* Moment of inertia
The moment of inertia, otherwise known as the mass moment of inertia, angular mass, second moment of mass, or most accurately, rotational inertia, of a rigid body is a quantity that determines the torque needed for a desired angular accele ...
* Perpendicular axis theorem The perpendicular axis theorem (or plane figure theorem) states that the moment of inertia of a planar lamina (i.e. 2-D body) about an axis perpendicular to the plane of the lamina is equal to the sum of the moments of inertia of the lamina about t ...
* Rigid body dynamics
In the physical science of dynamics, rigid-body dynamics studies the movement of systems of interconnected bodies under the action of external forces. The assumption that the bodies are ''rigid'' (i.e. they do not deform under the action of ...
* Stretch rule
In classical mechanics, the stretch rule (sometimes referred to as Routh's rule) states that the moment of inertia of a rigid object is unchanged when the object is stretched parallel to an axis of rotation that is a principal axis, provided tha ...
References
External links
{{commons category, Steiner's parallel axis theoremParallel axis theorem
Mechanics Physics theorems Christiaan Huygens Moment (physics) fr:Moment d'inertie#Théorème de transport (ou théorème d'Huygens ou théorème de Steiner)