Magnetic Flux on:
[Wikipedia]
[Google]
[Amazon]
In
 Gauss's law for magnetism, which is one of the four
Gauss's law for magnetism, which is one of the four
 While the magnetic flux through a closed surface is always zero, the magnetic flux through an open surface need not be zero and is an important quantity in electromagnetism.
When determining the total magnetic flux through a surface only the boundary of the surface needs to be defined, the actual shape of the surface is irrelevant and the integral over any surface sharing the same boundary will be equal. This is a direct consequence of the closed surface flux being zero.
While the magnetic flux through a closed surface is always zero, the magnetic flux through an open surface need not be zero and is an important quantity in electromagnetism.
When determining the total magnetic flux through a surface only the boundary of the surface needs to be defined, the actual shape of the surface is irrelevant and the integral over any surface sharing the same boundary will be equal. This is a direct consequence of the closed surface flux being zero.
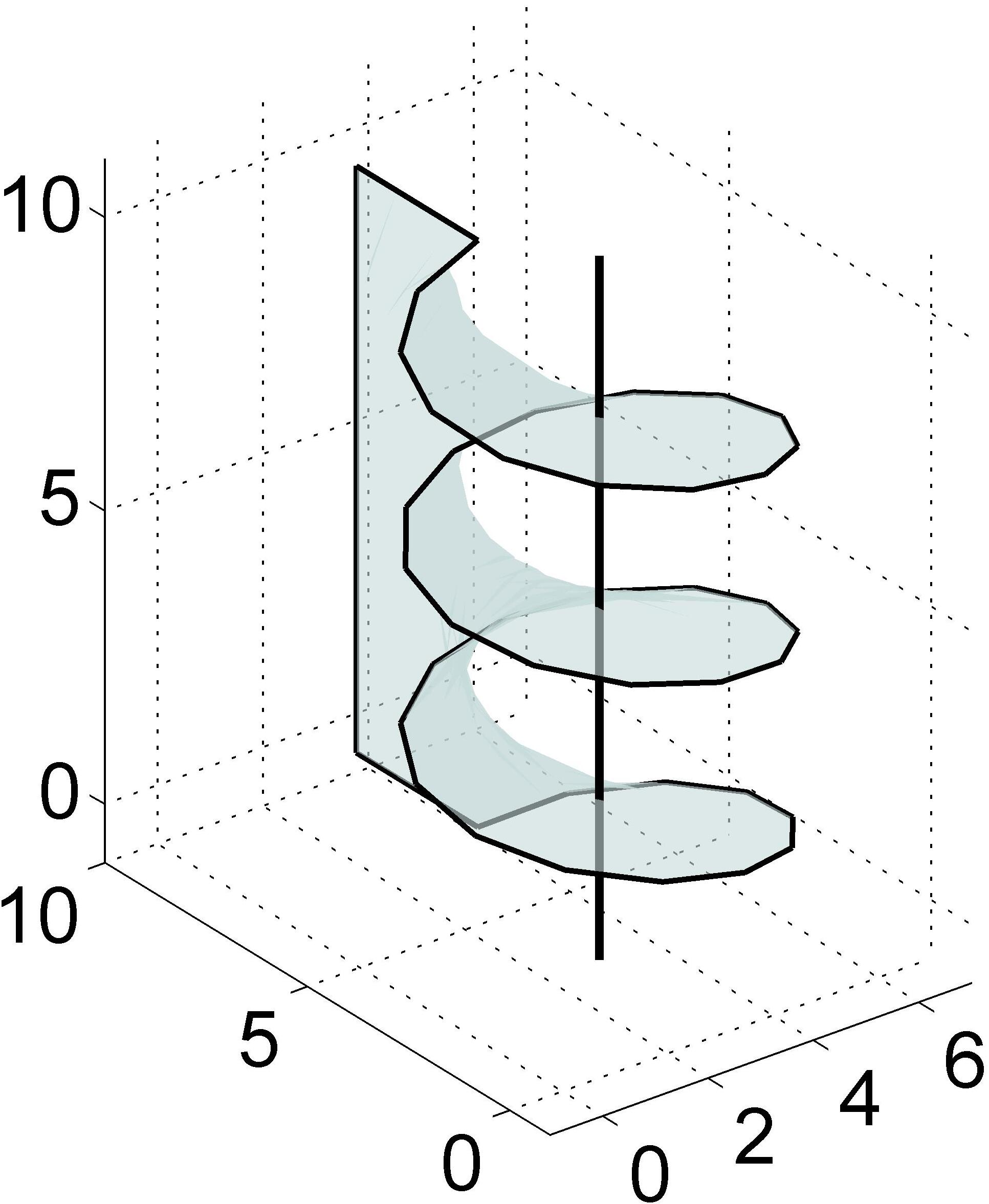
Magnetic Flux through a Loop of Wire
by Ernest Lee, Wolfram Demonstrations Project.
Conversion Magnetic flux Φ in nWb per meter track width to flux level in dB – Tape Operating Levels and Tape Alignment Levels
* wikt:magnetic flux {{Authority control Physical quantities Magnetism
physics
Physics is the natural science that studies matter, its fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge which ...
, specifically electromagnetism
In physics, electromagnetism is an interaction that occurs between particles with electric charge. It is the second-strongest of the four fundamental interactions, after the strong force, and it is the dominant force in the interactions o ...
, the magnetic flux through a surface is the surface integral
In mathematics, particularly multivariable calculus, a surface integral is a generalization of multiple integrals to integration over surfaces. It can be thought of as the double integral analogue of the line integral. Given a surface, one ...
of the normal component
In mathematics, given a vector at a point on a curve, that vector can be decomposed uniquely as a sum of two vectors, one tangent to the curve, called the tangential component of the vector, and another one perpendicular to the curve, called the n ...
of the magnetic field B over that surface. It is usually denoted or . The SI unit of magnetic flux is the weber
Weber (, or ; German: ) is a surname of German origin, derived from the noun meaning " weaver". In some cases, following migration to English-speaking countries, it has been anglicised to the English surname 'Webber' or even 'Weaver'.
Notable pe ...
(Wb; in derived units, volt–seconds), and the CGS unit is the maxwell
Maxwell may refer to:
People
* Maxwell (surname), including a list of people and fictional characters with the name
** James Clerk Maxwell, mathematician and physicist
* Justice Maxwell (disambiguation)
* Maxwell baronets, in the Baronetage of ...
. Magnetic flux is usually measured with a fluxmeter, which contains measuring coils and electronics
The field of electronics is a branch of physics and electrical engineering that deals with the emission, behaviour and effects of electrons using electronic devices. Electronics uses active devices to control electron flow by amplification ...
, that evaluates the change of voltage
Voltage, also known as electric pressure, electric tension, or (electric) potential difference, is the difference in electric potential between two points. In a static electric field, it corresponds to the work needed per unit of charge to ...
in the measuring coils to calculate the measurement of magnetic flux.
Description
The magnetic interaction is described in terms of a vector field, where each point in space is associated with a vector that determines what force a moving charge would experience at that point (see Lorentz force). Since a vector field is quite difficult to visualize at first, in elementary physics one may instead visualize this field with field lines. The magnetic flux through some surface, in this simplified picture, is proportional to the number of field lines passing through that surface (in some contexts, the flux may be defined to be precisely the number of field lines passing through that surface; although technically misleading, this distinction is not important). The magnetic flux is the ''net'' number of field lines passing through that surface; that is, the number passing through in one direction minus the number passing through in the other direction (see below for deciding in which direction the field lines carry a positive sign and in which they carry a negative sign). In more advanced physics, the field line analogy is dropped and the magnetic flux is properly defined as the surface integral of the normal component of the magnetic field passing through a surface. If the magnetic field is constant, the magnetic flux passing through a surface of vector area S is where ''B'' is the magnitude of the magnetic field (the magnetic flux density) having the unit of Wb/m2 ( tesla), ''S'' is the area of the surface, and ''θ'' is the angle between the magnetic field lines and the normal (perpendicular) to S. For a varying magnetic field, we first consider the magnetic flux through an infinitesimal area element dS, where we may consider the field to be constant: A generic surface, S, can then be broken into infinitesimal elements and the total magnetic flux through the surface is then thesurface integral
In mathematics, particularly multivariable calculus, a surface integral is a generalization of multiple integrals to integration over surfaces. It can be thought of as the double integral analogue of the line integral. Given a surface, one ...
From the definition of the magnetic vector potential A and the fundamental theorem of the curl the magnetic flux may also be defined as:
where the line integral
In mathematics, a line integral is an integral where the function to be integrated is evaluated along a curve. The terms ''path integral'', ''curve integral'', and ''curvilinear integral'' are also used; '' contour integral'' is used as well, ...
is taken over the boundary of the surface , which is denoted .
Magnetic flux through a closed surface
Maxwell's equations
Maxwell's equations, or Maxwell–Heaviside equations, are a set of coupled partial differential equations that, together with the Lorentz force law, form the foundation of classical electromagnetism, classical optics, and electric circuits ...
, states that the total magnetic flux through a closed surface is equal to zero. (A "closed surface" is a surface that completely encloses a volume(s) with no holes.) This law is a consequence of the empirical observation that magnetic monopoles have never been found.
In other words, Gauss's law for magnetism is the statement:
:
for any closed surface ''S''.
Magnetic flux through an open surface
Changing magnetic flux
For example, a change in the magnetic flux passing through a loop of conductive wire will cause an electromotive force, and therefore an electric current, in the loop. The relationship is given by Faraday's law: where * is the electromotive force ( EMF), * is the magnetic flux through the open surface , * is the boundary of the open surface ; the surface, in general, may be in motion and deforming, and so is generally a function of time. The electromotive force is induced along this boundary. * is an infinitesimal vector element of the contour , * is the velocity of the boundary , * is the electric field, * is the magnetic field. The two equations for the EMF are, firstly, the work per unit charge done against the Lorentz force in moving a test charge around the (possibly moving) surface boundary and, secondly, as the change of magnetic flux through the open surface . This equation is the principle behind anelectrical generator
In electricity generation, a generator is a device that converts motive power ( mechanical energy) or fuel-based power ( chemical energy) into electric power for use in an external circuit. Sources of mechanical energy include steam turbines, ...
.

Comparison with electric flux
By way of contrast,Gauss's law
In physics and electromagnetism, Gauss's law, also known as Gauss's flux theorem, (or sometimes simply called Gauss's theorem) is a law relating the distribution of electric charge to the resulting electric field. In its integral form, it st ...
for electric fields, another of Maxwell's equations
Maxwell's equations, or Maxwell–Heaviside equations, are a set of coupled partial differential equations that, together with the Lorentz force law, form the foundation of classical electromagnetism, classical optics, and electric circuits ...
, is
:
where
*E is the electric field,
*''S'' is any closed surface,
*''Q'' is the total electric charge
Electric charge is the physical property of matter that causes charged matter to experience a force when placed in an electromagnetic field. Electric charge can be ''positive'' or ''negative'' (commonly carried by protons and electrons res ...
inside the surface ''S'',
*''ε''0 is the electric constant (a universal constant, also called the " permittivity of free space").
The flux of E through a closed surface is ''not'' always zero; this indicates the presence of "electric monopoles", that is, free positive or negative charges
Charge or charged may refer to:
Arts, entertainment, and media Films
* ''Charge, Zero Emissions/Maximum Speed'', a 2011 documentary
Music
* ''Charge'' (David Ford album)
* ''Charge'' (Machel Montano album)
* '' Charge!!'', an album by The Aqu ...
.
See also
* Dannatt plates, thick sheets made of electrical conductors * Flux linkage, an extension of the concept of magnetic flux * Magnetic circuit is a closed path in which magnetic flux flows *Magnetic flux quantum
The magnetic flux, represented by the symbol , threading some contour or loop is defined as the magnetic field multiplied by the loop area , i.e. . Both and can be arbitrary, meaning can be as well. However, if one deals with the superconducti ...
is the quantum of magnetic flux passing through a superconductor
References
External articles
* *Magnetic Flux through a Loop of Wire
by Ernest Lee, Wolfram Demonstrations Project.
Conversion Magnetic flux Φ in nWb per meter track width to flux level in dB – Tape Operating Levels and Tape Alignment Levels
* wikt:magnetic flux {{Authority control Physical quantities Magnetism