Inner Automorphism

In abstract algebra an inner automorphism is an automorphism of a group, ring, or algebra given by the conjugation action of a fixed element, called the ''conjugating element''. They can be realized via simple operations from within the group itself, hence the adjective "inner". These inner automorphisms form a subgroup of the automorphism group, and the quotient of the automorphism group by this subgroup is defined as the outer automorphism group.

Definition

If is a group and is an element of (alternatively, if is a ring, and is a unit), then the function

:$\begin \varphi_g\colon G&\to G \\ \varphi_g(x)&:= g^xg \end$

is called (right) conjugation by (see also conjugacy class). This function is an endomorphism of : for all $x_1,x_2\in G,$

:$\varphi_g(x_1 x_2) = g^ x_1 x_2g = \left(g^ x_1 g\right)\left(g^ x_2 g\right) = \varphi_g(x_1)\varphi_g(x_2),$

where the second equality is given by the insertion of the identity between $x_1$ and $x_2.$ Furthermore, it has a left and right inverse, namely $\varphi_.$ Thus, $\varphi_g$ is bijective, and so an isomorphism of with itself, i.e. an automorphism. An inner automorphism is any automorphism that arises from conjugation.

When discussing right conjugation, the expression $g^xg$ is often denoted exponentially by $x^g.$ This notation is used because composition of conjugations satisfies the identity: $\left(x^\right)^ = x^$ for all $g_1, g_2 \in G.$ This shows that right conjugation gives a right action of on itself.

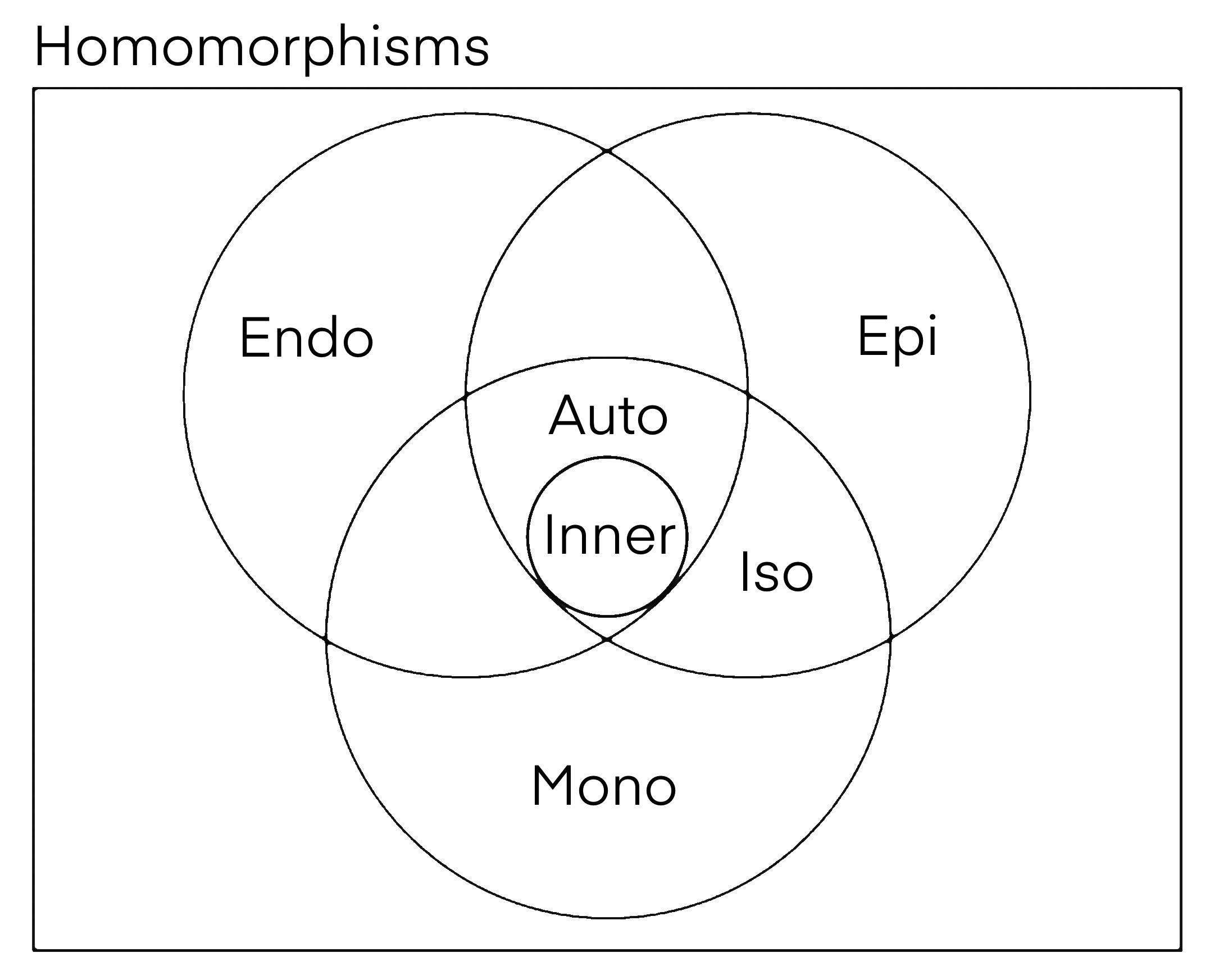
Inner and outer automorphism groups

The composition of two inner automorphisms is again an inner automorphism, and with this operation, the collection of all inner automorphisms of is a group, the inner automorphism group of denoted .

is a normal subgroup of the full automorphism group of . The outer automorphism group, is the quotient group
:$\operatorname(G) = \operatorname(G) / \operatorname(G).$

The outer automorphism group measures, in a sense, how many automorphisms of are not inner. Every non-inner automorphism yields a non-trivial element of , but different non-inner automorphisms may yield the same element of .

Saying that conjugation of by leaves unchanged is equivalent to saying that and commute:
:$a^xa = x \iff xa = ax.$

Therefore the existence and number of inner automorphisms that are not the identity mapping is a kind of measure of the failure of the commutative law in the group (or ring).

An automorphism of a group is inner if and only if it extends to every group containing .

By associating the element with the inner automorphism in as above, one obtains an isomorphism between the quotient group (where is the center of ) and the inner automorphism group:
:$G\,/\,\mathrm(G) \cong \operatorname(G).$

This is a consequence of the first isomorphism theorem, because is precisely the set of those elements of that give the identity mapping as corresponding inner automorphism (conjugation changes nothing).

Non-inner automorphisms of finite -groups

A result of Wolfgang Gaschütz says that if is a finite non-abelian -group, then has an automorphism of -power order which is not inner.

It is an open problem whether every non-abelian -group has an automorphism of order . The latter question has positive answer whenever has one of the following conditions:
# is nilpotent of class 2
# is a regular -group
# is a powerful -group
# The centralizer in , , of the center, , of the Frattini subgroup, , of , , is not equal to

Types of groups

The inner automorphism group of a group , , is trivial (i.e., consists only of the identity element) if and only if is abelian.

The group is cyclic only when it is trivial.

At the opposite end of the spectrum, the inner automorphisms may exhaust the entire automorphism group; a group whose automorphisms are all inner and whose center is trivial is called complete. This is the case for all of the symmetric groups on elements when is not 2 or 6. When , the symmetric group has a unique non-trivial class of non-inner automorphisms, and when , the symmetric group, despite having no non-inner automorphisms, is abelian, giving a non-trivial center, disqualifying it from being complete.

If the inner automorphism group of a perfect group is simple, then is called quasisimple.

Lie algebra case

An automorphism of a Lie algebra is called an inner automorphism if it is of the form , where is the adjoint map and is an element of a Lie group whose Lie algebra is . The notion of inner automorphism for Lie algebras is compatible with the notion for groups in the sense that an inner automorphism of a Lie group induces a unique inner automorphism of the corresponding Lie algebra.

Extension

If is the group of units of a ring, , then an inner automorphism on can be extended to a mapping on the projective line over by the group of units of the matrix ring, . In particular, the inner automorphisms of the classical groups can be extended in that way.

References

Further reading

*
*
*
*
*
*
*

{{DEFAULTSORT:Inner Automorphism
Group theory
Group automorphisms

de:Automorphismus#Innere Automorphismen