eight-vertex model on:
[Wikipedia]
[Google]
[Amazon]
In
 We consider a lattice, with vertices and edges. Imposing periodic boundary conditions requires that the states 7 and 8 occur equally often, as do states 5 and 6, and thus can be taken to have the same energy. For the zero-field case the same is true for the two other pairs of states. Each vertex has an associated energy and Boltzmann weight , giving the partition function over the lattice as
:
where the summation is over all allowed configurations of vertices in the lattice. In this general form the partition function remains unsolved.
We consider a lattice, with vertices and edges. Imposing periodic boundary conditions requires that the states 7 and 8 occur equally often, as do states 5 and 6, and thus can be taken to have the same energy. For the zero-field case the same is true for the two other pairs of states. Each vertex has an associated energy and Boltzmann weight , giving the partition function over the lattice as
:
where the summation is over all allowed configurations of vertices in the lattice. In this general form the partition function remains unsolved.
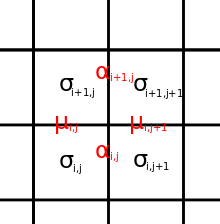 The most general form of the energy for this model is
:
where , , , describe the horizontal, vertical and two diagonal 2-spin interactions, and describes the 4-spin interaction between four faces at a vertex; the sum is over the whole lattice.
The most general form of the energy for this model is
:
where , , , describe the horizontal, vertical and two diagonal 2-spin interactions, and describes the 4-spin interaction between four faces at a vertex; the sum is over the whole lattice.
 We denote horizontal and vertical spins (arrows on edges) in the eight-vertex model , respectively, and define up and right as positive directions. The restriction on vertex states is that the product of four edges at a vertex is 1; this automatically holds for Ising 'edges'. Each configuration then corresponds to a unique , configuration, whereas each , configuration gives two choices of configurations.
Equating general forms of Boltzmann weights for each vertex , the following relations between the and , , , , define the correspondence between the lattice models:
:
It follows that in the zero-field case of the eight-vertex model, the horizontal and vertical interactions in the corresponding Ising model vanish.
These relations gives the equivalence between the partition functions of the eight-vertex model, and the 2,4-spin Ising model. Consequently a solution in either model would lead immediately to a solution in the other.
We denote horizontal and vertical spins (arrows on edges) in the eight-vertex model , respectively, and define up and right as positive directions. The restriction on vertex states is that the product of four edges at a vertex is 1; this automatically holds for Ising 'edges'. Each configuration then corresponds to a unique , configuration, whereas each , configuration gives two choices of configurations.
Equating general forms of Boltzmann weights for each vertex , the following relations between the and , , , , define the correspondence between the lattice models:
:
It follows that in the zero-field case of the eight-vertex model, the horizontal and vertical interactions in the corresponding Ising model vanish.
These relations gives the equivalence between the partition functions of the eight-vertex model, and the 2,4-spin Ising model. Consequently a solution in either model would lead immediately to a solution in the other.
statistical mechanics
In physics, statistical mechanics is a mathematical framework that applies statistical methods and probability theory to large assemblies of microscopic entities. It does not assume or postulate any natural laws, but explains the macroscopic b ...
, the eight-vertex model is a generalisation of the ice-type (six-vertex) models; it was discussed by Sutherland, and Fan & Wu, and solved by Baxter in the zero-field case.
Description
As with the ice-type models, the eight-vertex model is a square lattice model, where each state is a configuration of arrows at a vertex. The allowed vertices have an even number of arrows pointing towards the vertex; these include the six inherited from theice-type model In statistical mechanics, the ice-type models or six-vertex models are a family of vertex models for crystal lattices with hydrogen bonds. The first such model was introduced by Linus Pauling in 1935 to account for the residual entropy of water ice. ...
(1-6), and sinks and sources (7, 8).
 We consider a lattice, with vertices and edges. Imposing periodic boundary conditions requires that the states 7 and 8 occur equally often, as do states 5 and 6, and thus can be taken to have the same energy. For the zero-field case the same is true for the two other pairs of states. Each vertex has an associated energy and Boltzmann weight , giving the partition function over the lattice as
:
where the summation is over all allowed configurations of vertices in the lattice. In this general form the partition function remains unsolved.
We consider a lattice, with vertices and edges. Imposing periodic boundary conditions requires that the states 7 and 8 occur equally often, as do states 5 and 6, and thus can be taken to have the same energy. For the zero-field case the same is true for the two other pairs of states. Each vertex has an associated energy and Boltzmann weight , giving the partition function over the lattice as
:
where the summation is over all allowed configurations of vertices in the lattice. In this general form the partition function remains unsolved.
Solution in the zero-field case
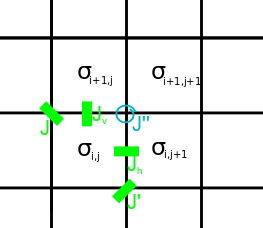
The zero-field case of the model corresponds physically to the absence of external electric fields. Hence, the model remains unchanged under the reversal of all arrows; the states 1 and 2, and 3 and 4, consequently must occur as pairs. The vertices can be assigned arbitrary weights : The solution is based on the observation that rows in transfer matrices commute, for a certain parametrisation of these four Boltzmann weights. This came about as a modification of an alternate solution for the six-vertex model; it makes use of elliptic theta functions.Commuting transfer matrices
The proof relies on the fact that when and , for quantities : the transfer matrices and (associated with the weights , , , and , , , ) commute. Using the star-triangle relation, Baxter reformulated this condition as equivalent to a parametrisation of the weights given as : for fixed modulus and and variable . Here snh is the hyperbolic analogue of sn, given by : and and areTheta functions
In mathematics, theta functions are special functions of several complex variables. They show up in many topics, including Abelian varieties, moduli spaces, quadratic forms, and solitons. As Grassmann algebras, they appear in quantum field ...
of modulus . The associated transfer matrix thus is a function of alone; for all ,
:
The matrix function
The other crucial part of the solution is the existence of a nonsingular matrix-valued function , such that for all complex the matrices commute with each other and the transfer matrices, and satisfy where : The existence and commutation relations of such a function are demonstrated by considering pair propagations through a vertex, and periodicity relations of the theta functions, in a similar way to the six-vertex model.Explicit solution
The commutation of matrices in () allow them to be diagonalised, and thuseigenvalues
In linear algebra, an eigenvector () or characteristic vector of a linear transformation is a nonzero vector that changes at most by a scalar factor when that linear transformation is applied to it. The corresponding eigenvalue, often denote ...
can be found. The partition function is calculated from the maximal eigenvalue, resulting in a free energy per site of
:
for
:
where and are the complete elliptic integrals of moduli and .
The eight vertex model was also solved in quasicrystals
A quasiperiodic crystal, or quasicrystal, is a structure that is ordered but not periodic. A quasicrystalline pattern can continuously fill all available space, but it lacks translational symmetry. While crystals, according to the classical ...
.
Equivalence with an Ising model
There is a natural correspondence between the eight-vertex model, and theIsing model
The Ising model () (or Lenz-Ising model or Ising-Lenz model), named after the physicists Ernst Ising and Wilhelm Lenz, is a mathematical model of ferromagnetism in statistical mechanics. The model consists of discrete variables that represent ...
with 2-spin and 4-spin nearest neighbour interactions. The states of this model are spins on faces of a square lattice. The analogue of 'edges' in the eight-vertex model are products of spins on adjacent faces:
:
 The most general form of the energy for this model is
:
where , , , describe the horizontal, vertical and two diagonal 2-spin interactions, and describes the 4-spin interaction between four faces at a vertex; the sum is over the whole lattice.
The most general form of the energy for this model is
:
where , , , describe the horizontal, vertical and two diagonal 2-spin interactions, and describes the 4-spin interaction between four faces at a vertex; the sum is over the whole lattice.
 We denote horizontal and vertical spins (arrows on edges) in the eight-vertex model , respectively, and define up and right as positive directions. The restriction on vertex states is that the product of four edges at a vertex is 1; this automatically holds for Ising 'edges'. Each configuration then corresponds to a unique , configuration, whereas each , configuration gives two choices of configurations.
Equating general forms of Boltzmann weights for each vertex , the following relations between the and , , , , define the correspondence between the lattice models:
:
It follows that in the zero-field case of the eight-vertex model, the horizontal and vertical interactions in the corresponding Ising model vanish.
These relations gives the equivalence between the partition functions of the eight-vertex model, and the 2,4-spin Ising model. Consequently a solution in either model would lead immediately to a solution in the other.
We denote horizontal and vertical spins (arrows on edges) in the eight-vertex model , respectively, and define up and right as positive directions. The restriction on vertex states is that the product of four edges at a vertex is 1; this automatically holds for Ising 'edges'. Each configuration then corresponds to a unique , configuration, whereas each , configuration gives two choices of configurations.
Equating general forms of Boltzmann weights for each vertex , the following relations between the and , , , , define the correspondence between the lattice models:
:
It follows that in the zero-field case of the eight-vertex model, the horizontal and vertical interactions in the corresponding Ising model vanish.
These relations gives the equivalence between the partition functions of the eight-vertex model, and the 2,4-spin Ising model. Consequently a solution in either model would lead immediately to a solution in the other.
See also
* Six-vertex model * Transfer-matrix method *Ising model
The Ising model () (or Lenz-Ising model or Ising-Lenz model), named after the physicists Ernst Ising and Wilhelm Lenz, is a mathematical model of ferromagnetism in statistical mechanics. The model consists of discrete variables that represent ...
Notes
References
*{{Citation , last1=Baxter , first1=Rodney J. , title=Exactly solved models in statistical mechanics , url=http://physics.anu.edu.au/theophys/_files/Exactly.pdf , publisher=Academic Press Inc. arcourt Brace Jovanovich Publishers, location=London , isbn=978-0-12-083180-7 , mr=690578 , year=1982 , access-date=2012-08-12 , archive-date=2021-04-14 , archive-url=https://web.archive.org/web/20210414063635/https://physics.anu.edu.au/theophys/_files/Exactly.pdf , url-status=dead Exactly solvable models Statistical mechanics Lattice models